基于数理统计的缺陷涡流检测定量方法
2020-12-19陈新波何忠祥李小丽
陈新波,何忠祥,李小丽,王 莉
(海军航空大学青岛校区 航空机械工程与指挥系,青岛 266041)
阻抗平面显示是涡流检测设备的主要显示方式,该显示方式对缺陷大小难以准确定量。在某型发动机叶片上加工不同长度的人工裂纹,将其作为检测对象,找出了涡流检测结果与裂纹长度的数学关系,该关系也可用于其他传感器或检测对象的定量评估。
1 定量方法
涡流检测采用阻抗平面图显示时,主要依靠幅值大小判断缺陷大小,不能准确评估。通过对涡流检测幅值进行定量研究,并对人工裂纹进行涡流检测试验,获得检测结果的幅值,采用正态分布和一元线性回归方法进行数据分析,得到裂纹大小和幅值的对应关系,定量方法框图如图1所示。

图1 涡流检测缺陷定量方法框图
2 叶片涡流检测试验
在工程实践中,涡流检测对象尺寸和厚度往往都随着检测位置的不同而不同,这些在涡流检测中会成为干扰因素[1]。为了使涡流检测的定量结论更具有参考性,检测时选择自身干扰因素较多的某型发动机Ⅰ级压气机叶片作为研究对象。
2.1 人工裂纹设计
根据标准GJB 2908-97《中华人民共和国国家军用标准涡流检测方法》,在某型发动机Ⅰ级压气机叶片上设计同一宽度、不同长度的人工裂纹,尺寸如表1所示。
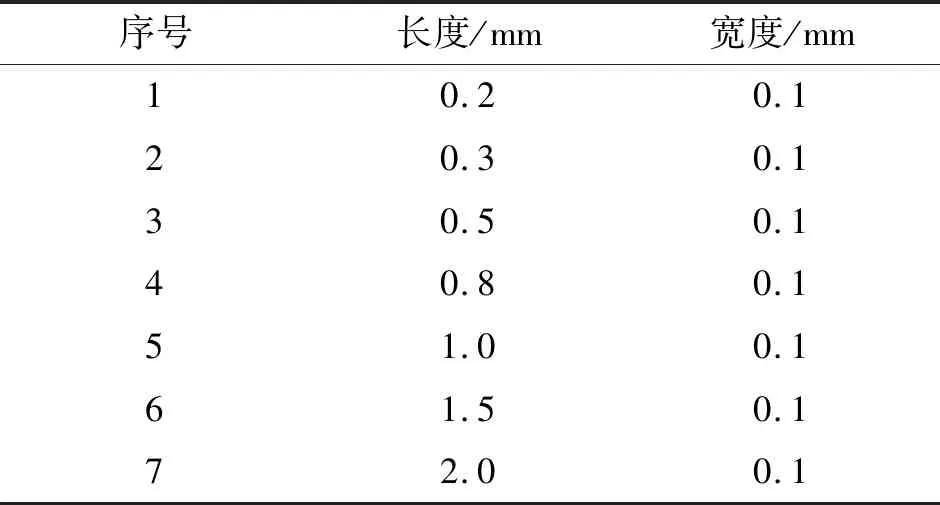
表1 某型发动机Ⅰ级压气机叶片人工裂纹尺寸
采用电火花加工法在某型发动机叶片上加工人工裂纹缺陷[2],其位置如图2所示。

图2 叶片人工裂纹位置示意
2.2 缺陷检测试验
用设计的人工裂纹叶片试块进行涡流检测试验,参数如表2所示。
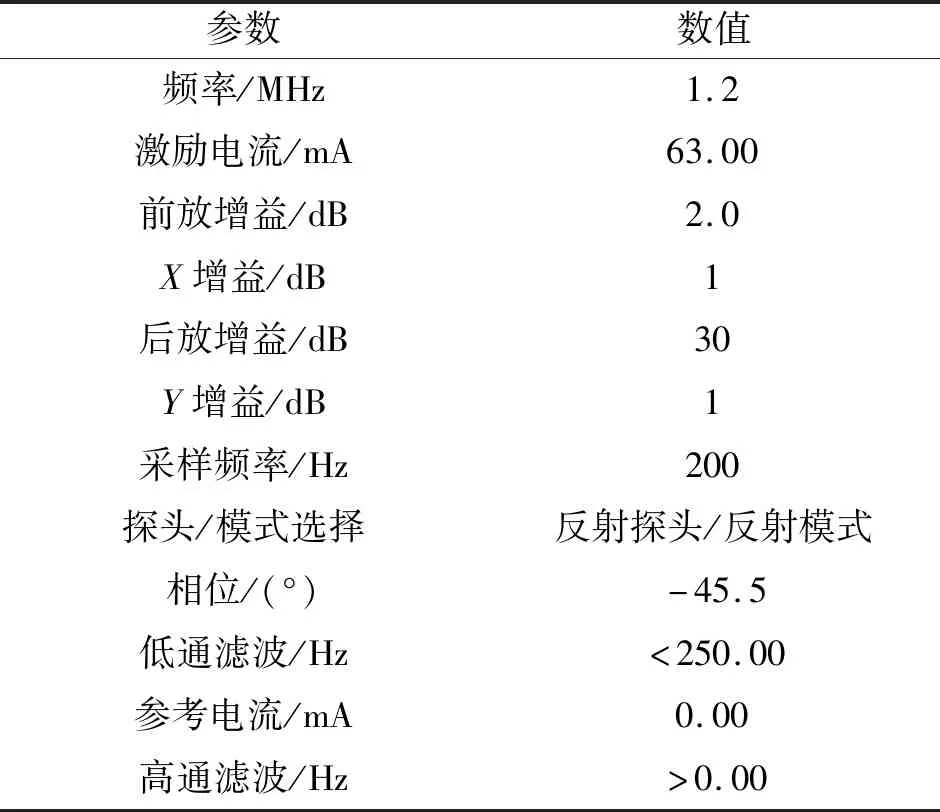
表2 人工裂纹叶片的涡流检测参数设置
经过大量检测试验可知:由于叶片厚度的影响,在阻抗图的模式下,涡流信号会发生零点漂移,遇到裂纹缺陷后,试件上涡流分布会发生较大变化,在阻抗图界面下表现为涡流信号的采样数据点轨迹发生突变,叶片缺陷检测信号轨迹如图3所示。

图3 叶片缺陷检测信号轨迹
通过研究数据点在有缺陷时信号轨迹的变化量来研究缺陷信号幅值,为了增加检测结果的可靠性,采集不同裂纹缺陷叶片的20次检测结果作为数据样本,叶片缺陷涡流检测信号幅值如表3所示。
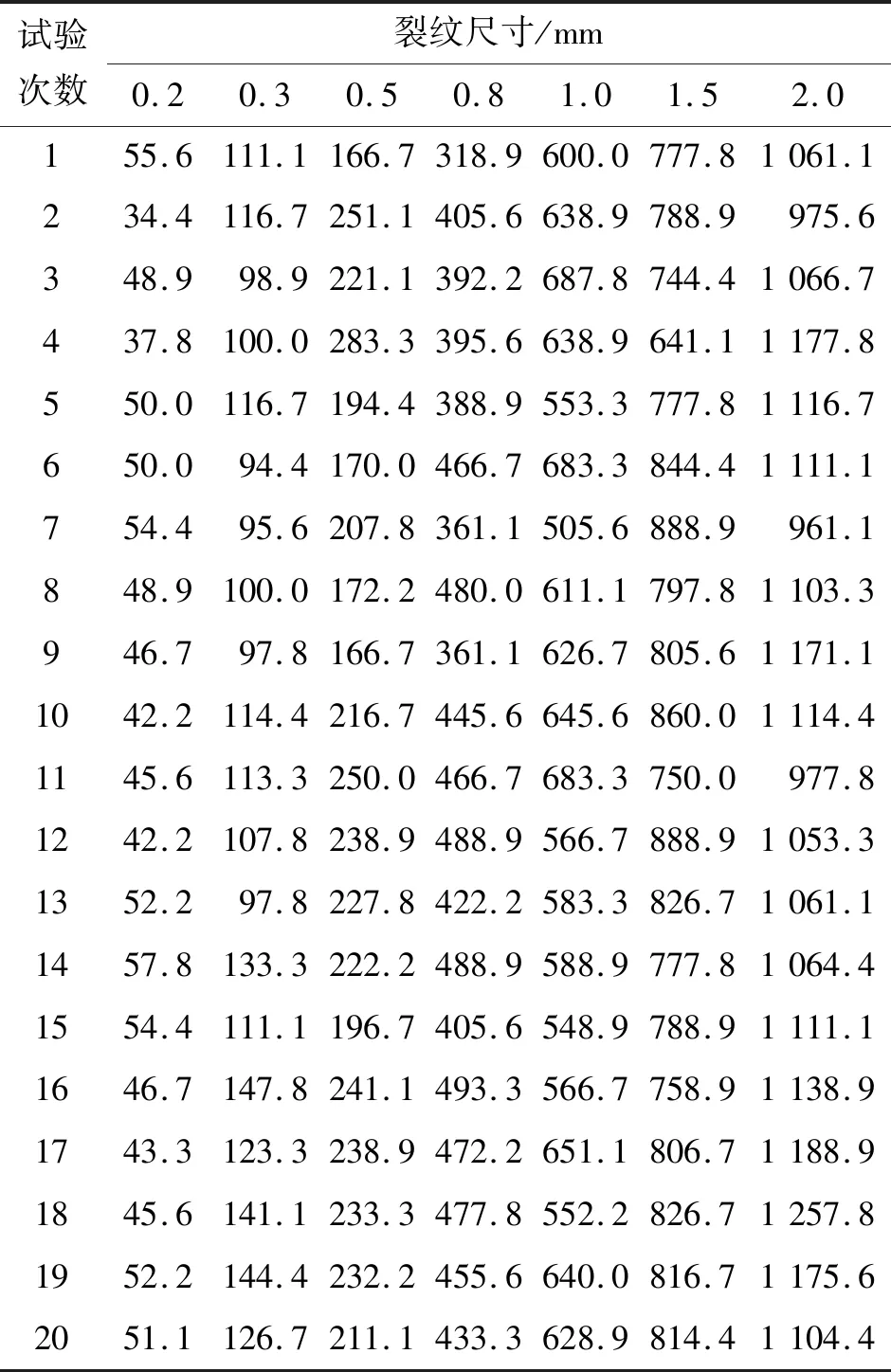
表3 叶片缺陷涡流检测信号幅值 mV
3 定量方法研究
3.1 正态分布分析
涡流检测的结果会受检测人员的操作水平、设备自身干扰以及叶片的厚度变化等诸多因素影响,且对结果的影响都是随机的[3],所以同一裂纹的检测信号在一定范围内是一个随机数,同一裂纹缺陷的信号幅值满足正态分布。设x为信号轨迹的幅值,根据正态分布的概率密度函数,则有
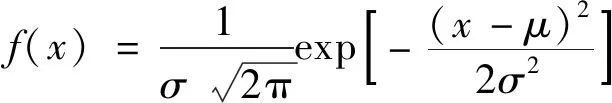
(1)
式中:x为信号阻抗幅值;μ为均值;σ为方差。
式(1)表示涡流测量结果信号阻抗幅值x服从均值为μ、方差为σ的正态分布,即x~N(μ,σ2)[4]。
根据正态分布概念,可以选取使得概率密度函数达到最大值的幅值x作为该裂纹缺陷的最佳检测结果,即在诸多影响因素作用下,每次检测结果的幅值都会在小范围内变化,并趋近于x。
采用Excel计算数据正态分布的概率密度:① 根据表3的检测幅值计算数组的均值、均方差、标准方差,结果如表4所示;② 利用Excel的函数NORMDIST得到每个测量值在数组中的概率正态分布值(以表3中1.0 mm裂纹缺陷的检测幅值为例);③ 绘制正态分布曲线,如图4所示;④ 读取分布曲线的峰值,即f(x)最大时x的值。
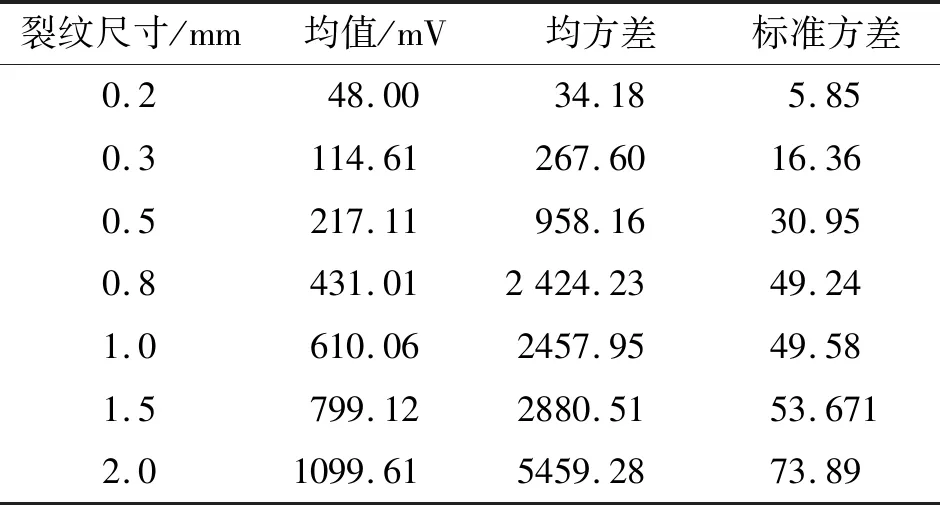
表4 裂纹检测幅值的统计计算结果
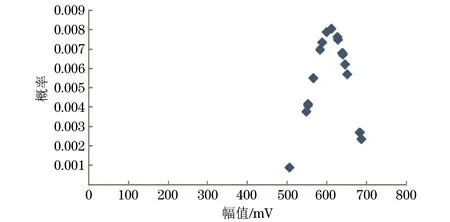
图4 1.0 mm裂纹缺陷幅值正态分布曲线
取概率密度最大值时对应的峰值幅值,结果如表5所示。
3.2 线性回归分析
观测表5的数值,该叶片不同缺陷的检测信号幅值在概率密度最大时基本满足线性分布,采用一元线性回归分析,拟合裂纹尺寸和峰值幅值的关系,从而对涡流检测结果进行定量。假设裂纹尺寸为x,峰值为y,则满足

表5 不同尺寸裂纹的峰值幅值
y=bx+a
(2)
式中:a,b为回归系数。
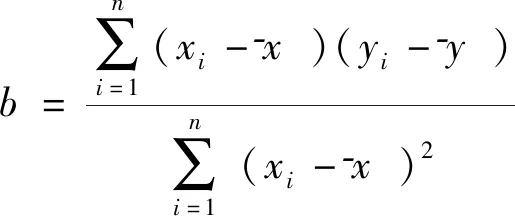
(3)
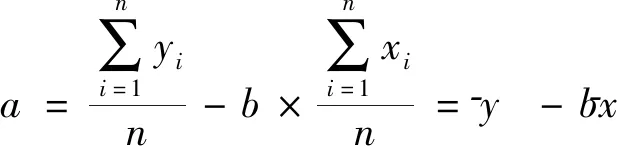
(4)
采用数据分析,裂纹长度与检测信号幅值的线性拟合曲线如图5所示。
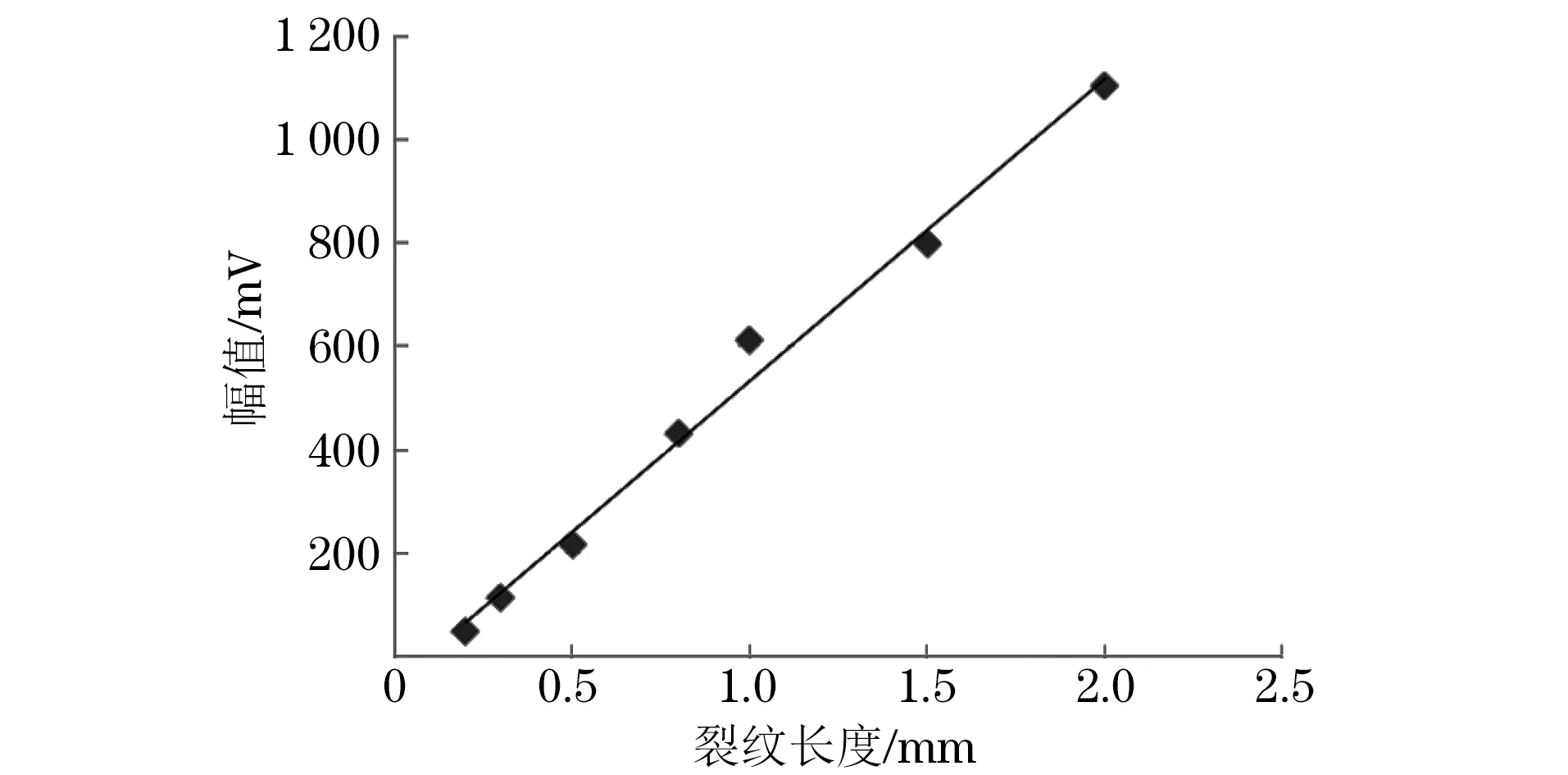
图5 裂纹长度与检测信号幅值的线性拟合曲线
(1) 设计的专用试块在按表2进行参数设置时,涡流检测结果具有良好的线性度,满足y=585.29x-51.531,且决定系数R2=0.990 8,表示回归模型系数的拟合优度较高[5],即裂纹尺寸在99.08%程度上与涡流检测结果幅值密切相关,更具有实践意义。
(2) 当采用一元m次多项式进行回归分析时,即=b0+b1x+b2x2+…+bmxm时,随着m的增大,R2也增大。
当m=2时,y=-61.296x2+717.41x-98.019,R2=0.993 7。
当m=3时,y=53.93x3-236.55x2+871.09x-129.08,R2=0.994 2。
当m=4时,y=437.86x4-1 853.3x3+2 501.4x2-586.8x+92.178,R2=0.998 5。
当R2增大时拟合度更高,但对发展趋势的预测不如m=1时的拟合度。
4 定量方法应用
根据3.2节得到的结论y=585.29x-51.531进行实际验证,能满足相应数学关系。对1.5 mm人工裂纹叶片进行涡流检测,经计算,检测结果幅值为790.0 mV,其检测结果阻抗图如图6所示。
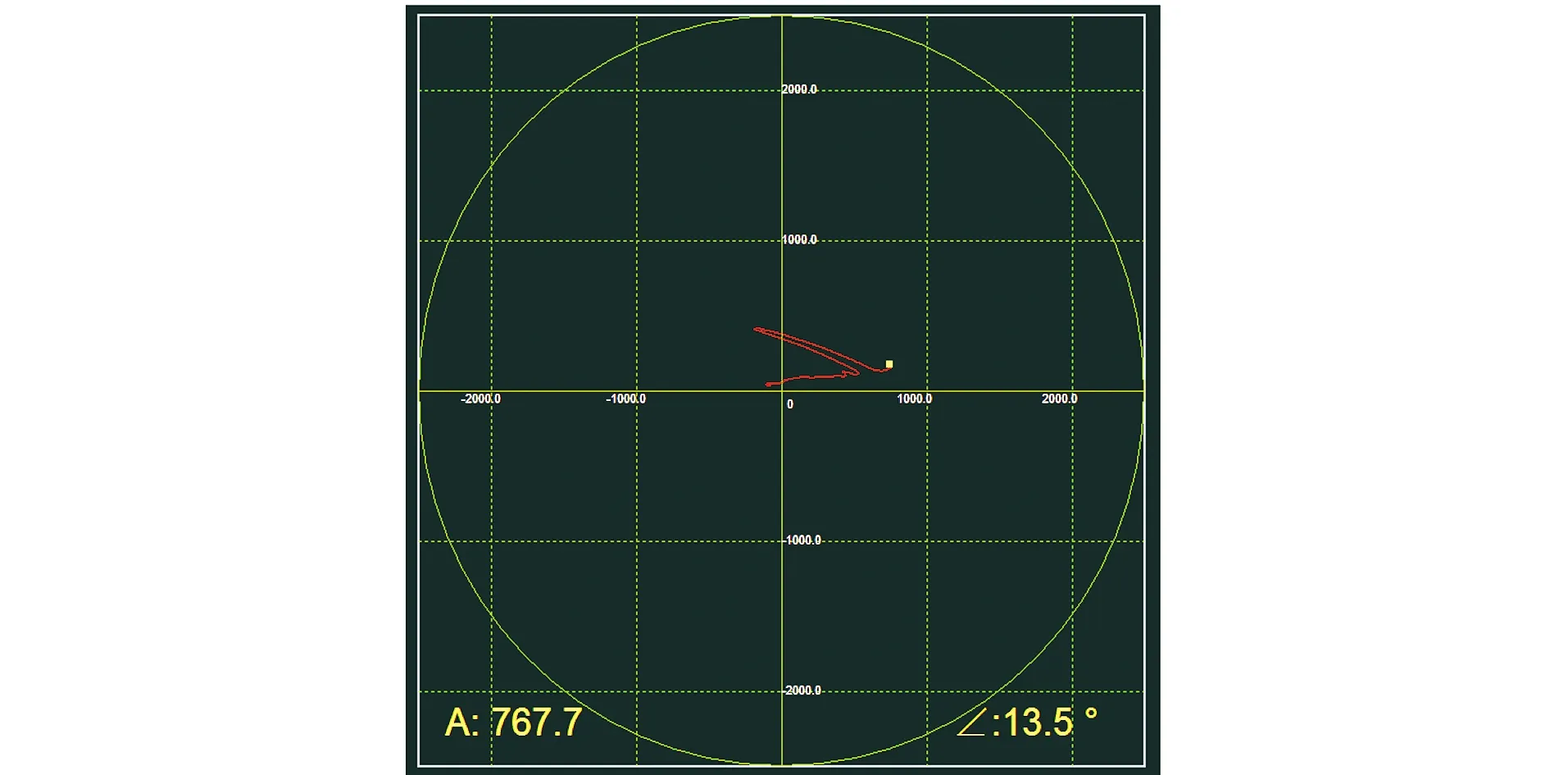
图6 1.5 mm叶片检测结果阻抗图
5 结论
(1) 在裂纹长度小于2.0 mm时,检测结果满足特定的线性规律:y=585.29x-51.531。
(2) 该方法具有参考性,当对其他检测设备和检测对象进行定量研究时,可采用图1的思路;定量研究不同裂纹深度和幅值关系时,也可以参照此方法。
(3) 对于智能涡流检测设备,可以参照图1的思路,增加计算幅值功能并建立数据库,由专业涡流检测人员通过试验录入数据,在智能系统中编写程序来计算定量关系式,并可将定量研究结果应用于实践中,为设备使用者提供相关参考依据,使得设备更加智能化,更具有可操作性。
