基于SVD的多用户大规模MIMO混合预编码算法

何晓华， 赵 峰

(桂林电子科技大学 信息与通信学院，广西 桂林 541004)

毫米波频段在30～300 GHz能够提供更多的频谱资源，成为未来通信最有前景的技术之一[1-3]。毫米波较短的波长使得天线尺寸更小，因而，能在有限的空间里部署更多的天线，促进大规模多输入多输出(mutil-input mutil-ouput，简称MIMO)系统的发展，同时，大规模MIMO能够为系统提供更多的空间增益[4-6]，以弥补毫米波较高的路径损耗。然而传统的全数字预编码算法需要与天线数目等同的射频链路，使得全数字预编码的毫米波大规模MIMO系统的实现需要高成本、高功耗[7]。

为了减少射频链路，混合预编码成为毫米波大规模MIMO系统的研究热点。现有的主流混合预编码[8-11]将预编码分为模拟域和数字域两部分，模拟域使用低成本的相移器减少射频链路，数字域使用低维的基带预编码实现用户之间的干扰管理。基于多用户毫米波MIMO系统，Liang等[8]提出相移迫零(phased-zero forcing，简称PZF)混合预编码，提取聚合信道的相移部分设计模拟域预编码，获取阵列增益，数字域通过迫零(zero forcing，简称ZF)预编码抑制用户之间的干扰。Ni等[9]在文献[8]的基础上进行了拓展，考虑多用户多流的通信场景，数字域通过块对角化(block diagonalization，简称BD)实现多用户多流之间的干扰抑制。文献[8-9]的混合预编码算法要求射频链路的数目必须等于用户数，且对信道的状态信息要求较高，不符合实际应用要求。文献[10-11]提出了几种基于码本的迭代混合预编码算法，系统的频谱效率接近最优，但由于每次迭代涉及矩阵求逆和分解等操作，随着天线数目的增加，矩阵的运算会越来越复杂，导致系统的复杂度较高。

Zhang等[12]提出了信道的右酉矩阵直接设计模拟域预编码方法，但该方法针对提高单用户大规模MIMO系统的频谱效率，不易于扩展至多用户大规模MIMO系统。鉴于此，针对多用户单天线大规模MIMO系统，提出基于奇异值分解(singular value decomposition，简称SVD)的混合预编码算法。

1 系统模型

考虑单小区下行毫米波大规模MIMO系统，系统模型如图1所示。在该系统中，基站配备Nt根发送天线和NRF个射频链路，发送Ns个数据流到K个单天线用户。与传统的大规模MIMO系统不同，毫米波大规模MIMO系统中射频链路的数目远小于天线数目，即满足Ns≤NRF≤Nt。

图1 毫米波大规模 MIMO系统混合预编码结构

根据上述模型，发送端的发送信号可以表示为

x=VRFVBBs。

(1)

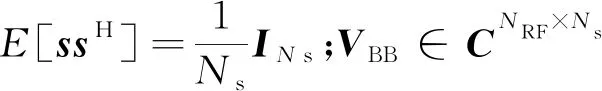
在毫米波信道下，用户k接收到的信号可表示为

k=1,2,…,K

(2)

其中：hk为基站到第k个用户的下行信道矩阵；VBB，k为第k列数字域预编码矩阵，VBB，j为第j列数字域预编码矩阵；sj为s的第j个元素；nk为第k个用户的高斯白噪声，且服从CN(0,δ2)。因此，第k个用户的信干噪比(signal-to-interference-plus-noise-ratio，简称SINR)可表示为

(3)

则系统获得的总频谱效率为

(4)

2 信道模型

由于自由空间的高路径损耗，毫米波传播环境的特点是分簇信道模型，因此采用文献[13]提出的Saleh-Valenzuela信道模型，其信道矩阵可表示为

(5)

(6)

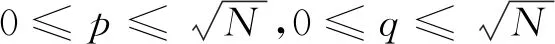
3 混合预编码设计

3.1 问题描述

利用图1的系统结构来设计混合预编码，混合预编码的数字域预编码VBB能够对输入的信号进行振幅和相位处理，模拟域预编码VRF只能对输入的信号进行相位处理。将设计毫米波大规模MIMO系统的混合预编码建模成一个频谱优化问题：

|VRF(i,j)|=1,∀i,j。

(7)

由于优化问题具有固定模约束，且2个变量是耦合的非凸优化问题，不易直接解决优化问题。因此，将式(7)优化问题分解成两级优化问题来设计混合预编码，使系统的频谱效率接近最优。

3.2 模拟预编码设计

首先设计模拟域预编码，对于模拟域预编码的设计不考虑用户之间的干扰。利用等效信道[8]的概念，即Heq=HVRF，使得用户的等效信道最优化。

等效信道最优化问题：

(8)

由于式(8)仍然是基于固定模限制的非凸优化问题，直接解决还是不易。因此，考虑无固定模限制的最优化预编码。对于无限制的最优化模拟预编码，利用对信道的SVD来求解：

(9)

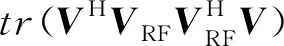
将有模限制模拟预编码问题转化为求其与无固定模限制的的最优化的模拟域预编码最小欧式距离，表达式为

(10)

可进一步将问题(10)改写为

(11)

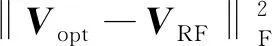
VRF=[v1,v2,…,vNRF],

其中，vj=[ejφ1,j,ejφ2,j,…,ejφNt,j]T,φi,j为Vopt矩阵每个元素的相移。

3.3 数字预编码设计

信号经过模拟域处理后，数字域的性能主要取决于系统的信道矩阵与模拟域预编码矩阵作用后所产生的等效信道矩阵Heq。因此，传统的全数字线性预编码可以应用于数字域消除用户间的干扰。在多用户MIMO中最常用的线性预编码方案为ZF预编码、BD预编码以及最小均方误差(minimum mean square error，简称MMSE)预编码。

用ZF预编码设计数字域预编码为

(12)

用MMSE预编码设计数字域预编码为

(13)

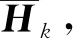
(14)

(15)

(16)

其中Nu表示每个用户接收的数据流数。因此，用BD设计的基带数字域预编码为

(17)

为了满足功率约束要求，对数字域预编码VBB进行归一化，归一化的数字预编码

本算法主要分为2个阶段：1)通过提取信道的右奇异矩阵设计模拟域预编码，避免了复杂的迭代；2)基于等效信道，设计数字域预编码,消除用户间的干扰。

4 仿真结果与分析

为了进一步分析所提出的混合预编码算法，用MATLAB对混合预编码算法进行性能仿真分析。设发射端采用均匀方形平面阵列(USPA)，每个阵元之间的间距为λ/2，λ为传输信号的波长。信道参数设置为：路径数为Nray=10，方位离开角AOD和方位到达角AOA服从拉普拉斯分布，簇角度在[0,2π]上服从均匀分布，且角度拓展为10°，发射端配备天线数目Nt=64，接收端用户数为K=9，数据流等于射频链路数，即Ns=NRF。

4.1 完美信道

图2为Ns=NRF=K时在输入不同信噪比的情况下，不同混合预编码算法在完美信道状态条件下所获得的频谱效率。从图2可看出，基于SVD的混合预编码相较于文献[8]的PZF预编码方案能够获得更高的频谱效率，更接近全数字预编码算法，且随着信噪比的增加，2种混合预编码算法的差距更加明显。基于SVD的混合预编码SVD-MMSE获得的频谱效率较高，SVD-ZF获得的频谱效率较低。为了分析多用户多流毫米波大规模MIMO系统的性能，图3仿真了当Ns=NRF=2K时在输入不同信噪比的情况下，不同混合预编码算法在完美信道状态条件下所获得的频谱效率。由于文献[8]中混合预编码设计要求射频链路的数目必须等于用户数目，在图3中未与文献[8]进行仿真比较。从图3可看出，所提出的混合预编码算法在多用户多流通信场景中，依然能够获得较高的频谱效率。

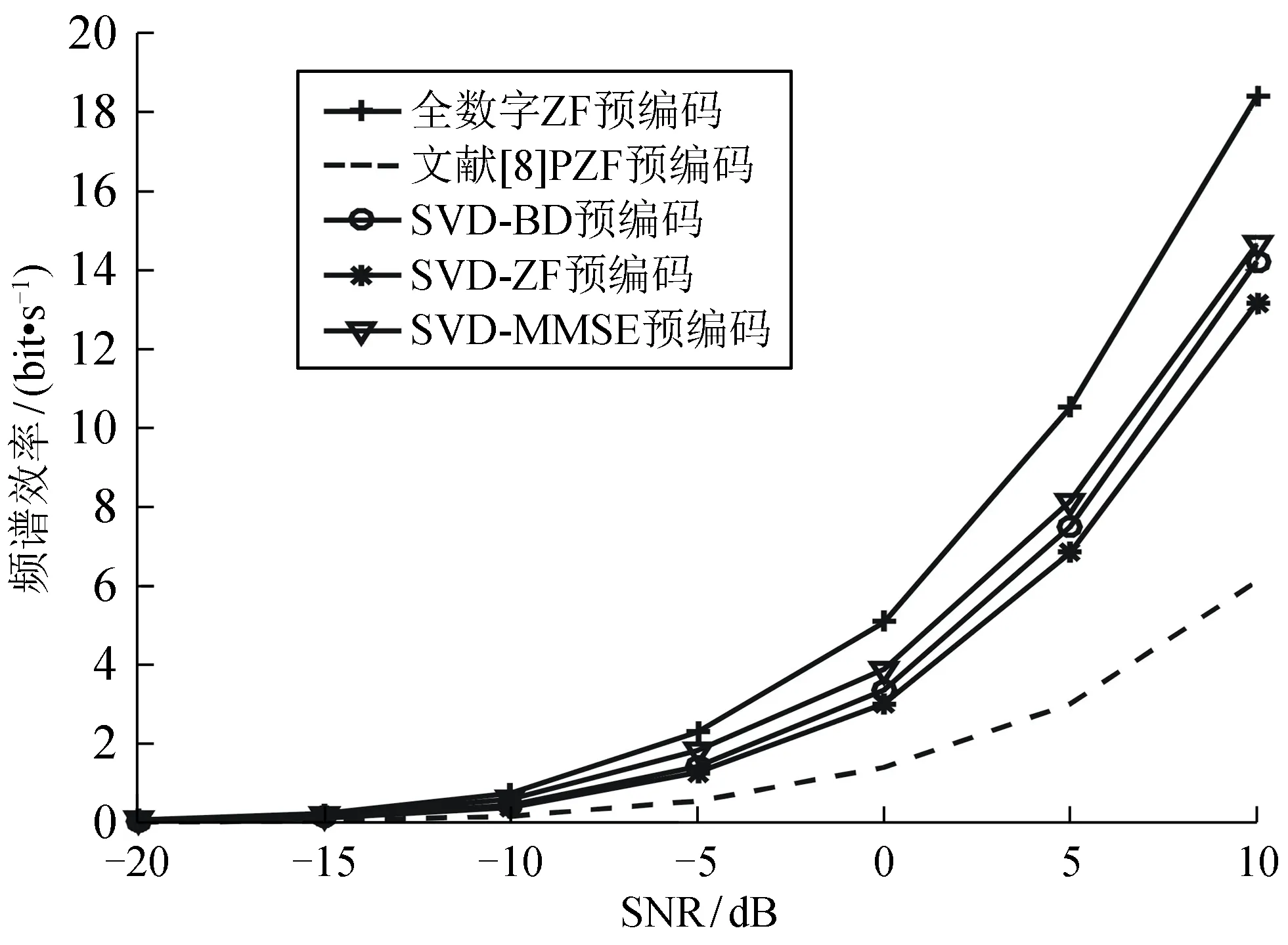
图2 Ns=NRF=K时完美信道下的频谱效率

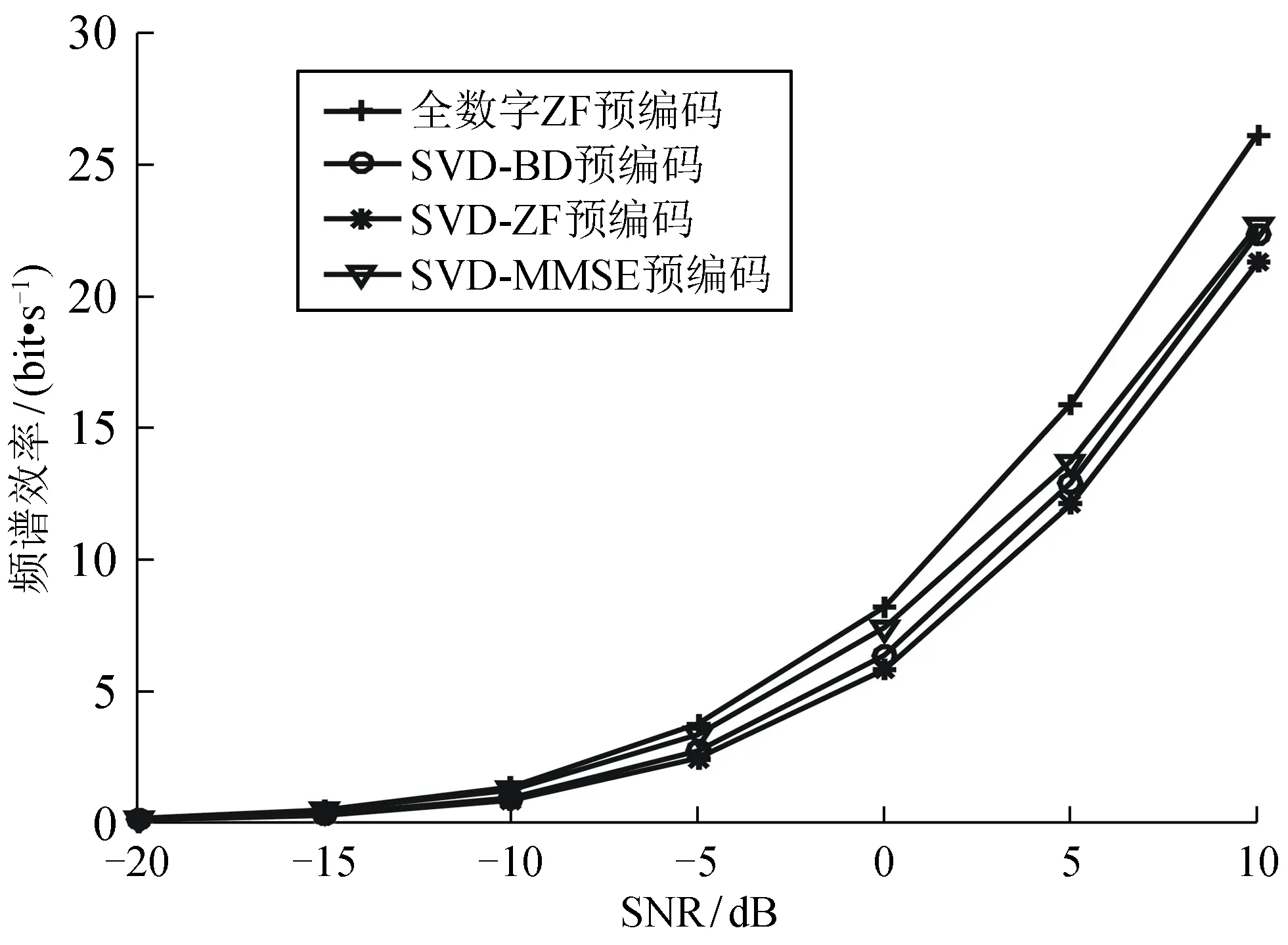
图3 Ns=NRF=2K时完美信道下的频谱效率

4.2 非完美信道

在实际应用中，由于基站与用户之间缺少协作，以及一些不确定因素，如不精确的信道估计、有限反馈等，完美的信道状态信息很难获得。因此，考虑在非完美信道状态信息条件下，对提出的混合预编码算法性能仿真分析。对于信道状态信息的估计，采用最小均方误差信道估计方法[14]，表达式为

(18)

图4为Ns=NRF=K时在非完美信道状态信息条件下，随着SNR的变化，不同预编码算法频谱效率的变化情况。从图4可看出，所提出的混合预编码算法相较于文献[8]的混合预编码算法，在非完美信道状态信息条件下，能够获得更高的频谱效率。另外，结合图2、图4可知，相较于完美信道状态条件下，非完美信道状态条件下几种预编码算法所获得频谱效率都有所下降，SVD-MMSE算法频谱效率下降最多，对系统的性能鲁棒性较差。

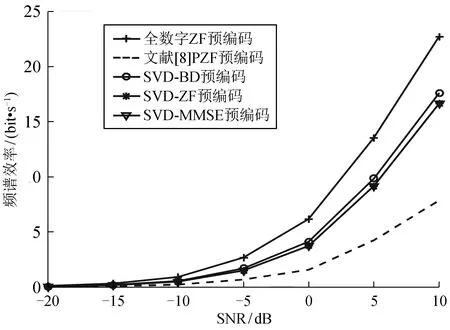
图4 NRF=Ns=K时非完美信道下的频谱效率

5 结束语

针对多用户毫米波大规模MIMO提出的基于SVD分解的混合预编码算法，无需优化方法或任何复杂的迭代设计，且易于扩展到多用户多天线以及多流场景。仿真分析表明，与文献[8]提出的PZF混合预编码算法比较，基于SVD的混合预编码算法在完美信道状态条件下和非完美状态信道条件下都能获得更高的频谱效率。今后将研究毫米波大规模MIMO系统中部分连接混合预编码算法。