基于NMPC-PID的无人机控制算法
2020-12-18谭惠东李天松卢艳菊严一超
谭惠东, 李天松, 莫 雄, 卢艳菊, 严一超
(桂林电子科技大学 信息与通信工程学院,广西 桂林 541004)
四旋翼无人机因体积小、结构简单、机动性能好等特点,使其由单一的航模玩具领域不断向着遥感、航拍、地图绘制、军事侦察、火灾搜救、公安追捕等领域发展,具有非常广泛的研究价值和市场前景[1]。它通过4个电机的不同输入可实现对姿态和位置的调整。由于它拥有4个输入量,具有6个自由度,是一个欠驱动非线性系统,同时各通道之间具有强耦合关系[2],使得对无人机控制性能有较高要求。
传统的PID算法因其稳定性高且不依赖于精准模型的特点被广泛应用于无人机控制算法,但在面对风扰影响时,由于参数难以实时调整,无人机飞行受到限制。在此基础上,文献[3]提出了改进型的双闭环PID控制算法,该算法提高了四旋翼无人机抗干扰能力,但依赖于精确模型,且当外界干扰发生变化时难以适应。文献[4]采用模糊PID来实现四旋翼无人机姿态控制,具有鲁棒性好、调节速度快、超调量小等优点,但模糊控制规则因无成熟的设计方法而难以制定。
在风扰影响下,由于风对无人机产生的力的作用存在不确定性,传统PID控制算法无法使无人机保持稳定。针对这一问题,设计了NMPC-PID无人机控制算法,可对下一时刻无人机机身所受荷载进行预测,并自适应调整PID控制参数。仿真结果表明,NMPC-PID无人机控制算法可提高无人机的抗风能力,实验验证了本控制算法具有适应外界风速变化的特点。
1 四旋翼无人机数学模型建立
四旋翼无人机通过对电机转速的改变,可以实现无人机升力的变化,从而引起无人机姿态和位置的改变。由于PID控制算法的输出为控制电压,可以直接控制电机转速来影响无人机的运动状态,通过PID参数对无人机姿态和高度进行建模,能够更为直观地反映无人机姿态与高度的调整。四旋翼无人机运动规律可从牛顿-欧拉公式得到[5]:
(1)
(2)

(3)
其中:K为增益;T为时间常数。
增益K可通过测试四旋翼无人机的螺旋桨升力得到。将四旋翼无人机放在电子秤上,先测量无人机质量,当给定电机电压时,旋翼开始旋转并产生升力,总质量的减少量即为螺旋桨升力[7]。通过拟合,可得增益K约为0.936。
时间常数T为转速阶跃响应上升到稳态值的0.632倍时的时间。经测量,时间常数T约为0.178 s。因此,电机的传递函数为
(4)
1.1 高度控制模型
对于高度控制,假设只考虑Z轴的改变,保持其他轴不变,仅使用式(1)中的
(5)
已知Z轴误差值eZ为
eZ=Zref-Z>0,
(6)

(7)
同时PID的传递函数为[8]
(8)
其中Kp、Ki、Kd为PID控制算法参数。因此,整个系统的闭环传递函数为
(9)
其中,KB=0.9362,KC=0.178。
1.2 姿态控制模型
四旋翼无人机的姿态仅受横滚角、俯仰角、偏航角的影响,所以选取式(1)中的3个式子进行分析:
(10)
经简化,对其进行拉普拉斯变换,得到四旋翼姿态装置的横滚、俯仰、偏航的传递函数[9]:
(11)
其中:Ixx、Iyy、Izz为各轴的转动惯量;L为无人机质心与旋翼中心的距离。
PID控制算法误差计算式为
(12)
其中:θref、φref、φref为理想值;θ、φ、φ为输入值。
通过电机的闭环传递函数,姿态角闭环传递函数可表示为
(13)
(14)
2 NMPC-PID控制算法设计
传统的PID控制算法参数难以实时改变,因此跟踪风速变化的能力较弱。当受风扰影响时,固定的PID参数难以做出快速而准确的变化,无人机的室外飞行能力受到限制。因此,采用基于动态递归神经网络的NMPC-PID控制算法。相较于本质为静态网络的前馈神经网络,动态递归神经网络具有自身反馈特性,其反馈的内容中存有上一时刻的输入输出信息,因而具有动态建模能力且更容易收敛,更适用于非线性系统。NMPC-PID控制算法框图如图1所示。

图1 NMPC-PID控制算法框图
从图1可看出,NMPC-PID控制算法运用了基于NNI神经网络的系统辨识器和基于NNC神经网络的优化控制器2个神经网络。NMPC-PID控制算法的工作原理为在对控制对象在线辨识的基础上,通过对NNC神经网络的权系数进行实时调整,使系统具有自适应性,从而达到有效控制的目的[10]。
神经网络训练的目标函数[11]为
(15)

(16)
yr(k+j)为柔化序列,其动态方程为
(17)
其中:a为柔化因子,它是系统时间常数的理想值,柔化因子越小表示系统反应越快;r(k)为当前时刻设定值。
2.1 基于神经网络NNI的系统辨识器设计
在风扰情况下,无人机控制系统具有强非线性的特点,传统的PID控制算法难以应对这一情况,因此采用基于对角递归神经网络的辨识器对下一时刻系统所受荷载进行预测。对角递归神经网络是一种特殊的动态递归神经网络,具有结构相对简单且可处理非线性问题的特性。对角递归神经网络结构如图2所示。

图2 对角递归神经网络结构
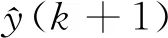
(18)
其中:n为系统输出的阶次;W(k)为所有神经元的权值组成的权值向量。该辨识系统输入输出表达式[10]为
(19)
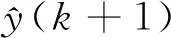
根据对角递归神经网络结构对权值调整算法进行修正,输入层权值调整算法修正为
Wj,o(k)f′(Sj(k))Zj(k-1)。
(20)
隐含层权值调整算法修正为
(21)
NNI神经网络训练的目标函数为
(22)
通过BP算法可以修正权值[10]:
(23)
2.2 基于NNC神经网络的优化控制器设计
由于增量式PID受误差的影响,设计优化控制算法NNC的输入参数为
(24)
NNC的输出结果为PID控制参数,优化神经网络NNC训练的目标函数[11]为
(25)
其权值Wc修正方法为
(26)
其中,
(27)
l可取p、i、d。
3 仿真与实验
对建立的模型以及控制算法进行MATLAB仿真,以验证本设计的控制系统的有效性。四旋翼无人机仿真初始参数设置如表1所示。
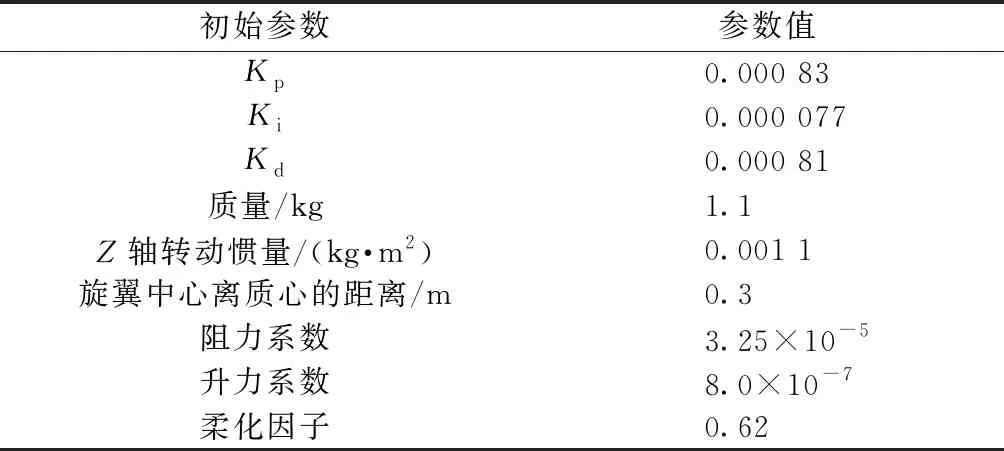
表1 四旋翼无人机仿真初始参数设置
设定高度理想值为1 m,系统阶跃相应测试结果如图3所示。从图3可看出,虽然传统PID算法与NMPC-PID算法具有类似特性,但是传统PID算法最大超调量为15.2%,NMPC-PID算法的最大超调量为3.5%,传统PID控制算法比NMPC-PID控制算法超调严重,且到达稳定的时间比NMPC-PID控制算法长,当风力发生变化时,阻力系数会随之改变。图4为阻力系数逐渐改变时横滚角曲线与阶跃响应比较。从图4可看出,初始时传统PID控制算法超调量较大,响应时间长,在第一个阶跃响应时,可以趋于平稳,但随着阻力系数的改变,传统PID控制算法开始出现震荡,难以适应阻力系数的变化,且无法保持平稳,而NMPC-PID控制算法通过预测下一时刻荷载并实时调整PID参数,可以一直保持稳定的周期性变化。
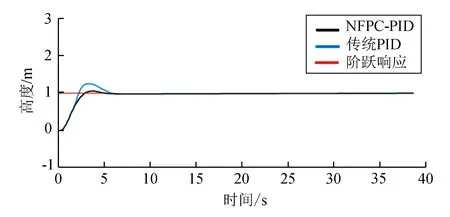
图3 2种算法高度变化曲线与阶跃响应比较
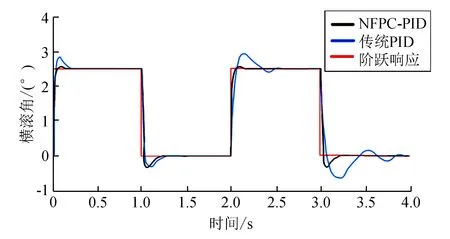
图4 阻力系数逐渐改变时横滚角曲线与阶跃响应比较
为了验证NMPC-PID控制算法在风扰时的控制情况,采用自制的四旋翼无人机进行定点悬停实验。所用四旋翼无人机如图5所示。
设定初始状态时无人机高度为1 m,姿态角均为0°。对无人机3个姿态角进行采样,采样时间间隔为100 ms。用电机旋转带动桨叶产生风,通过风速仪测量风速,约为8.3 m/s,在5级风力的范畴。图6为采用传统PID控制算法的无人机悬停时俯仰角变化曲线。从图6可看出,在约10 s处加入单向风干扰后,无人机姿态角发生了持续剧烈抖动,抖动范围为-12.32°~9.87°,无法进入稳定状态。图7为采用NMPC-PID控制算法的无人机悬停时俯仰角变化曲线。从图7可看出,在约10 s处加入单向风干扰,无人机在受到干扰后10 s内有较大程度的抖动,抖动范围为-9.53°~10.32°。之后,逐渐趋于稳定,并使抖动范围减小到-3.98°~5.36°,标准差为2.566,相较于采用传统PID控制算法的无人机减少了42.09%。在风扰情况下,分别采用NMPC-PID控制算法和传统PID控制算法的无人机悬停时偏航角和横滚角变化如表2所示。从表2可看出,采用NMPC-PID控制算法的无人机抖动范围为稳定以后的抖动范围,而采用传统PID控制算法的无人机因难以跟踪风力的变化而难以趋于稳定,抖动范围较大。采用NMPC-PID控制算法的无人机虽然开始受风扰时抖动明显,但最终能够趋于稳定。

图5 本实验的四旋翼无人机
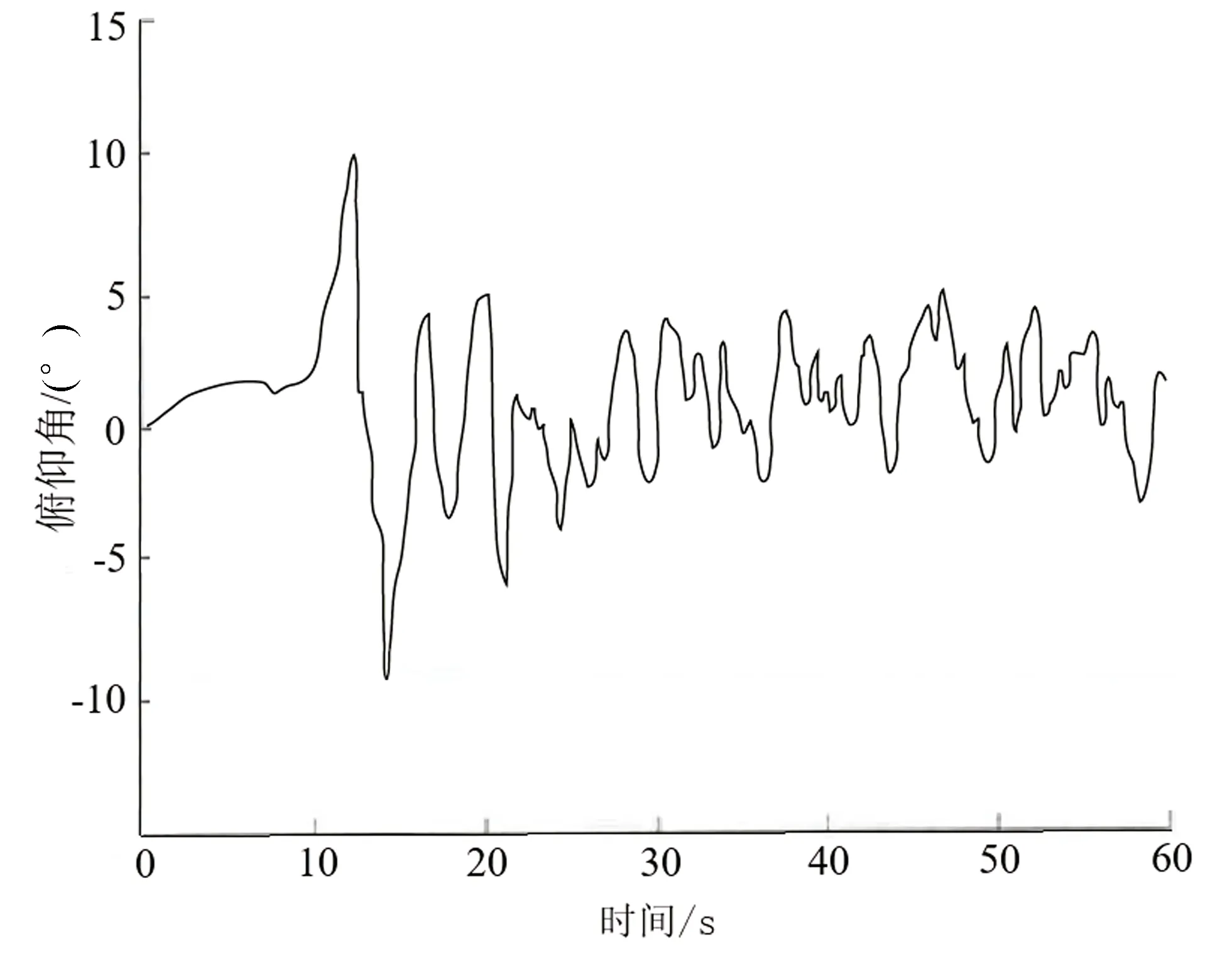
图7 NMPC-PID控制算法的无人机悬停时俯仰角变化曲线

表2 NMPC-PID控制算法与传统PID控制算法的横滚角及偏航角比较
通过仿真与实验分析可知,采用NMPC-PID控制算法的无人机具有超调量小,抗干扰性能强,鲁棒性好,能够适应风速变化的优点。
4 结束语
针对无风扰情况下采用传统PID控制算法的无人机难以“御风飞行”的情况,构建了四旋翼无人机数学模型,设计了NMPC-PID控制算法,并将NMPC-PID控制算法与传统PID控制算法进行对比仿真实验。模型的建立使高度与姿态角直接受PID参数控制,控制算法的设计使无人机在风扰情况下能够自适应调节PID参数。仿真结果表明,NMPC-PID控制算法较传统PID控制算法提高了抗干扰能力与鲁棒性,且具有超调量小的特点。通过对比实验,验证了NMPC-PID控制算法的可行性,比传统PID控制算法更能适应风的影响,在风中能够趋于稳定。
