应用于高速数据采集系统的超低抖动时钟电路

2020-12-18李海涛李斌康阮林波张雁霞

数据采集与处理 2020年6期

李海涛，李斌康，2，阮林波，2，田耕，2，张雁霞，2

（1.西北核技术研究所，西安，710024；2.强脉冲辐射环境模拟与效应国家重点实验室，西安，710024）

引言

近些年来，国内对高速数据采集系统的研究如火如荼，取得很多的成果。在高速数据采集系统中，有几个性能经常被比较提出，包括：模拟输入带宽、采样率、分辨率、有效位和存储深度等，前4 个指标主要由数据采集系统前端来决定（数字增强型的输入带宽、数字增强型的分辨率和数字增强型的有效位不在讨论之列）。数据采集系统的前端主要包括了前端模拟信号调理电路、模拟数字转换器（Analog to digital converter, ADC）、超低抖动时钟产生电路等。

目前，很多应用场合都使用具有高采集率、高分辨率的ADC，为充分利用ADC 的带宽、采样率、分辨率和有效位等性能，必须为ADC 选择极低噪声的模拟信号调理电路、超低抖动的时钟产生电路和超低纹波电源产生电路等。以下将重点讨论ADC 的有效位指标，影响ADC 的有效位（Effective number of bits，ENOB）的因素很多，包括 ADC 自身因素（ADC 的孔径抖动（Aperture jitter）、ADC 的量化噪声（Quantization noise）、ADC 的非线性等、模拟输入信号噪声、采样时钟抖动、电源纹波噪声等，信噪比（Signal to noise ration, SNR）具体可参考式（1），该公式的描述中未体现电源纹波噪声，或者已经将电源纹波噪声等效在其他因素中[1‑5]。

式中：fin为满量程（ADC 输入量程）模拟输入的标准正弦波频率；tjrms为ADC 的孔径抖动和采样时钟抖动的均方根值；ε为ADC 的非线性，包含了积分非线性和微分非线性；N为ADC 量化位数；VNOISErms为模拟输入噪声。在模拟输入满量程（不考虑幅度修正问题）且tjrms=0、ε=0、VNOISErms=0 的情况下，仅考虑ADC 量化噪声贡献，得到ADC 的理想信噪比为

式中信纳比(Signal to noise and distortion ratio，SINAD)为信号功率与噪声、谐波功率之比；ENOB 为ADC 的实际有效位数。

在模拟输入满量程且ε=0、VNOISErms=0 的情况下，将量化噪声等效到tjrms中，得到仅由抖动贡献的SINAD（如式（3））[6]。此处亦可以考虑成将其余因素全部等效为抖动tjrms的贡献，则

在模拟输入满量程且tjrms=0、VNOISErms=0 的情况下，将量化噪声等效到ε中，得到仅由非线性动贡献的SINAD（如式（4））。此处亦可以考虑成，将其余因素全部等效为非线性ε的贡献。

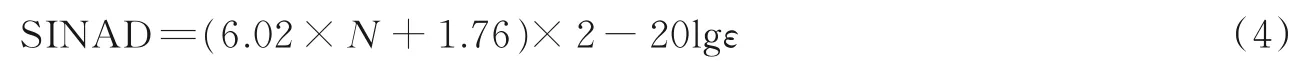
可以看到，fin、tjrms、ε、VNOISErms与外部输入相关，可以通过降低采样时钟抖动、降低电源噪声和提高模拟输入信号品质等途径，提高ADC 的有效位数ENOB[7]。应用举例：在输入信号频率fin=125 MHz且要求ADC 有效位ENOB=10 bits 情况下，根据式（2，3）得到：等效抖动tjrms=1.02 ps，此处的等效抖动包括了ADC 的自身因素和各种外界因素的贡献，实际对采样时钟抖动的要求更高。若在输入信号频率fin=125 MHz 且要求 ADC 有效位 ENOB=14 bits 情况下，根据式（2）和式（3）得到：等效抖动tjrms=64 fs。可以看出，对于高频输入模拟信号且高有效位的ADC 设计，低抖动的时钟设计是一个关键，降低采样时钟抖动，不仅能够提高ADC 有效位ENOB，还能够提高ADC 的模拟输入带宽[8]。

1 时钟相位噪声和时钟抖动

数据采集系统中经常提到的时钟相位噪声和时钟抖动指标，两者是同一项时钟性能在频域和时域的不同表现形式，本质是衡量时钟短期稳定性的指标。时钟的长期稳定性使用频率漂移（Frequency drift）来描述，其短期稳定性使用时钟抖动（Clock jitter）或者时钟相位噪声（Clock phase noise）来描述[9‑11]。

时钟抖动（Clock jitter）。表示时钟抖动的方法有多种[12]：周期抖动（Period jitter）、周期到周期抖动（Cycle to cycle jitter）、时间间隔误差（Time interval error）等，其中周期抖动比较常见。

相位噪声。L(f)定义为在1 Hz 的带宽划分下，频率fm处的功率与时钟中心频率f0（亦称载波频率fc）的功率之比，如式（5），一般用 dBc/Hz 表示[13]，有的文献中将S(fm)写成 PN(fm)，其中S代表频谱（Spec‑trum）；PN 代表相位噪声，S(f)为时钟的功率谱密度 (Power spectrum density，PSD)函数，单位为 W/Hz。

以下讨论的时钟抖动指的是时钟周期抖动，将时钟周期抖动和相位噪声关联起来并进行相互转换，需要借助于相位抖动（Phase jitter）。相位抖动定义为相位噪声功率谱密度上一定频带内的相位噪声能量总和，如式（6），单位弧度，式中，f1，f2为频率积分区间的下限、上限。相位抖动是一个频域的概念，频域的相位抖动和时域的周期抖动之间换算关系为

关于相位抖动的频率积分区间[f1，f2]，理论上讲，积分区间下限f1应该尽量低，f1为1 Hz、10 Hz 等，带宽上限应尽量高，f2为2f0、+∞。实际使用时，需要根据应用场合调整频率积分区间[12]，例如：光纤通道的时钟抖动的积分区间为[637 kHz,10 MHz]，10 GHz 以太网XAUI 中时钟抖动的积分区间为[1.875 MHz,20 MHz]，SATA/SAS 的时钟抖动的积分区间为[900 kHz,7 MHz][14]。

2 时钟产生电路

根据以上理论分析，为了使ADC 芯片可以实现最佳性能，需要为其提供超低抖动的时钟信号。选用了HITTITE 公司（已被ADI 收购）的HMC1035LP6GE[15‑17]（以下简称HMC1035）时钟产生芯片（或称为频率综合芯片），设计实现了超低抖动时钟产生电路，主要验证以下功能：（1）实现整数模式和小数模式下时钟频率输出，比较两者的时钟抖动。（2）整数模式下鉴相频率（Phase detector frequency, PFD）对输出时钟抖动的影响。（3）供电电源对HMC1035 输出的影响等。HMC1035 工作在整数模式、50 MHz 输入、2 500 MHz 输出的时钟抖动典型值为 97 fs[12 kHz,20 MHz]，622.08 MHz 输出的时钟抖动典型值为107 fs[12 kHz,20 MHz]。

图1 为时钟产生电路的原理图。高稳参考信号源采用的是 Crystek 公司的 CCHD‑950‑25‑100M：输出频率为100 MHz[18]，实际测量其时钟抖动为135 fs[10 kHz,10 MHz]；高速信号扇出芯片采用HITTITE公司的HMC987LP5GE 芯片[19]，用于低噪声时钟分配，可以完成1∶9 扇出缓冲器功能。

PCB 设计采用了 4 层板结构：L1（TOP，Signal）→L2（GND）→L3（Power）→L4（Bottom，Signal），FR‑4 板材，1.6 mm 标准厚度。设计时，TOP 层、Bottom 层走线阻抗控制，单线特征阻抗50 Ω，差分线特征阻抗100 Ω，Top、Bottom 层表面铺铜接地。电源设计采用外部电源供电，分析了2 种供电方式对HMC1035输出频率的影响。关于高速电路的电源去耦的设计，有很多专门的文章进行论述[20‑23]，这里不再赘述。

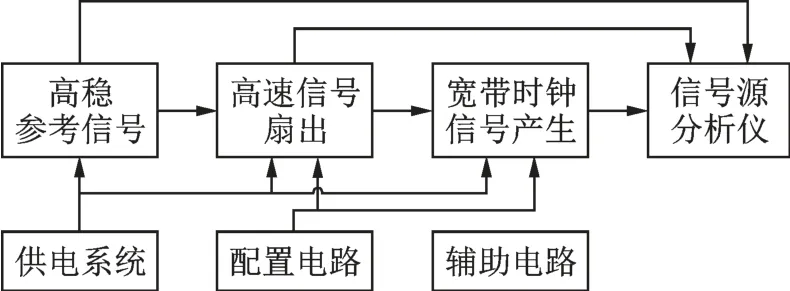
图1 时钟产生电路原理图Fig.1 Block diagram of clock generation circuit

HMC1035 窄带环路滤波的设计关系到PLL 的频率锁定和时钟噪声滤除[24‑25]：宽带滤波器有利于锁定但不利于滤除噪声，窄带滤波器有利于滤除噪声但不利于锁定，最终使用器件手册上给出的127 kHz 的无源四阶低通环路滤波器。

需要特别指出的是，在工作时，高速芯片引脚的连接，除了给定的NC 引脚可以悬空之外，在芯片工作时需要使用的引脚，不推荐悬空，引脚一旦悬空，容易导致引脚状态未知，影响系统的稳定。设计的时钟产生电路实物图如图2 所示。

图2 时钟产生电路实物Fig.2 Clock generating circuit photo

3 时钟电路测试

时钟抖动测试仪器采用ROHDE&SCHWARZ 公司的FSW13 频谱与信号分析仪，采用标准配件，在进行频谱分析时，积分区间[10 kHz,10 MHz]。

3.1 整数模式和小数模式下的时钟抖动比较

采用直流电压源供电，直流电压源型号Agilent E3631A，通过SPI 配置HMC1035 芯片，测量HMC1035 在整数模式和小数模式输出时钟的抖动，其它工作条件都相同，得到表1。表1 中HMC1035 2500 MHz‑50M Hz‑integer 表示 HMC1035 频率综合芯片工作条件为整数模式、50 MHz 鉴相器（Phase detector，PD）频率、2 500 MHz 压控振荡器（Voltage controlled oscillator，VCO）频率。HMC1035 2 500 MHz‑50 MHz‑fractional 表示 HMC1035 频率综合芯片工作条件为小数模式、50 MHz PD 频率、2 500 MHz VCO 频率。测量得到高稳参考信号输出的100 MHz 对应的时钟抖动典型值为135 fs（以下简称为100 MHz VCXO jitter），高速信号扇出后的100 MHz 信号时钟抖动典型值为152 fs（以下简称为HMC987 fanout jitter），以下表1 重复部分不再赘述。

表1 整数模式和小数模式对HMC1035 芯片输出性能的影响Table 1 Comparison of integer mode and fractional mode on output performance of HMC1035 chip

整数模式下锁相环（Phase lock loop, PLL）的输出分频率受限于PD 的频率步进。小数模式的优点在于可以提高PLL 的输出分辨率，显著改善锁定时间，但是小数模式下工作的PLL 的输出杂散水平较高，影响时钟抖动指标。可以看到：小数模式下的输出时钟抖动明显高于整数模式下的输出时钟抖动[26‑27]。原因在于整数模式下，不使用Σ‑Δ 调制器，降低了引入的时钟抖动。按照抖动的平方根值理论，可以看到Σ‑Δ 调制器的抖动贡献约为(1232-982)0.5=74 fs（2 500 MHz 输出频率，单次，未考虑统计涨落）。此处同时给出2 488,622,77.76 MHz 的输出时钟抖动测量值，是为了与手册给出的典型值进行对比。

3.2 整数模式下PD 工作频率对时钟抖动的影响

采用直流电压源供电，HMC1035 工作在整数模式下，PD 工作频率为 100，50，10，1 MHz，测量输出时钟抖动性能，结果如表2 所示，分析PD 工作频率对输出时钟抖动的影响。

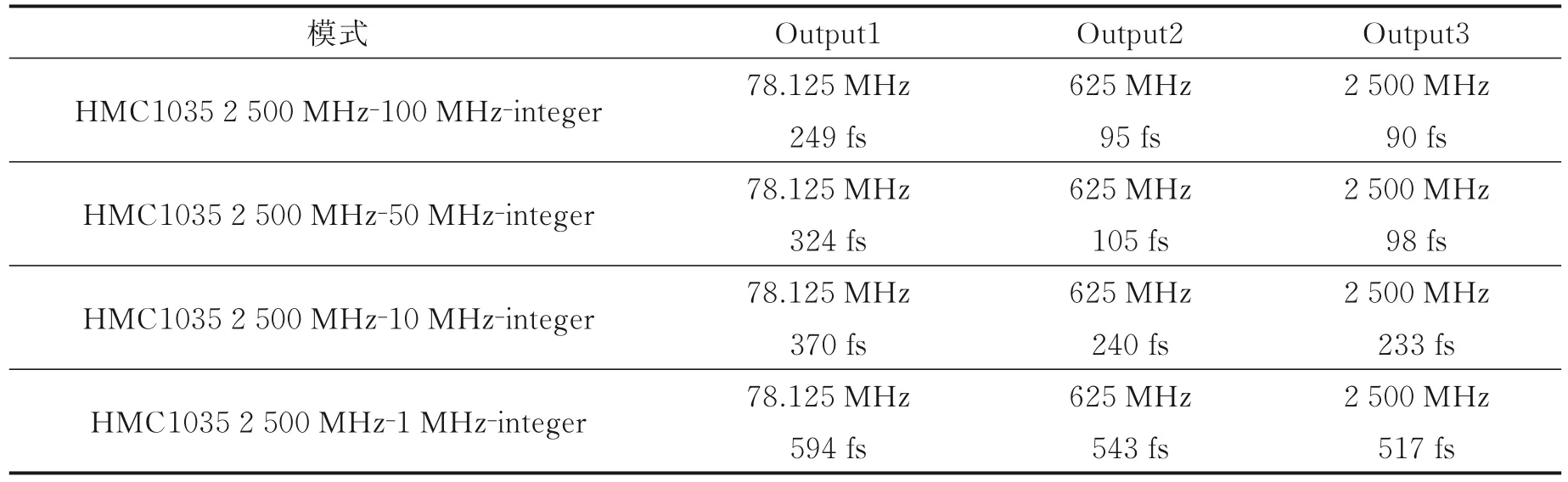
表2 PD 工作频率对HMC1035 芯片输出性能的影响Table 2 Comparison of PD operating frequency on output performance of HMC1035 chip

PD 有2 个输入端，一端接参考输入频率fxtal的R分频，一端接VCO 工作频率fVCO的N分频。PD 稳定工作在整数模式时，PD 无偏置，电流为0，此时，只需要考虑PD 工作频率fPD对输出时钟抖动的贡献，fPD表示为

PD 将fVCO的N分频的反馈频率与输入参考频率的某一分频形式进行鉴相，输出一个电流，经过积分和外部环路滤波，产生一个电压，这个电压驱动VCO 提高或者降低频率，使PD 的输出电流的等效电压接近0，达到平衡。提高fPD，可以降低输出时钟相位噪声，相位噪声是在PD 的最高工作频率上加20 logR，因此R越大，PD 工作频率越低，相位噪声越差，R增大一倍，相位噪声降低3 dB，应该使用可行的PD 最高工作频率，但实际往往需要均衡[28‑29]。文章表格描述的大部分HMC1035 的输出时钟抖动都是基于50 MHz 的fPD，该fPD为器件手册推荐工作频率；但是fPD为100 MHz 时，HMC1035 的输出时钟抖动指标更优，只是锁定时间增加，功耗增加。

3.3 整数模式下供电电源对时钟抖动的影响

HMC1035 芯片在正常工作时，其功耗比较高，为保证PLL 的输出性能，需要选择好供电方式，并做好电源的去耦和PCB 散热等工作。在保证电源去耦的前提下，分析了直流电压源（Agilent E3631A）供电和DC/DC 开关电源（PTH08T240W）供电对PLL 芯片输出性能的影响，如表3 所示。另外给出了直流电压源供电时HMC1035 的典型相位噪声曲线（图3）。

表3 直流供电和DC/DC 电源供电对HMC1035 芯片输出性能的影响Table 3 Comparison of DC power supply and DC/DC power supply on output performance of HMC1035 chip

可以看出，开关电源供电对整个系统的性能影响很大，不仅增加了HMC1035 的输出时钟抖动，而且增加了信号路径上的所有时钟抖动。开关电源供电对HMC1035 的输出时钟抖动贡献较大，预估约为90 fs（2 500 MHz 输出频率，单次，未考虑统计涨落），其贡献主要来源于开关频率及其高次谐波的影响。采用外部直流电压源供电后，HMC1035 的输出频谱上，在300 kHz 的开关频率附近依然有毛刺，如图3 所示。这是因为 SPI 配置 HMC1035、HMC987 的工作状态的芯片由开关电源供电，SPI 配置线路上未做好隔离处理，电源噪声通过SPI 配置线路耦合到HMC1035 电路板上引起[30]。

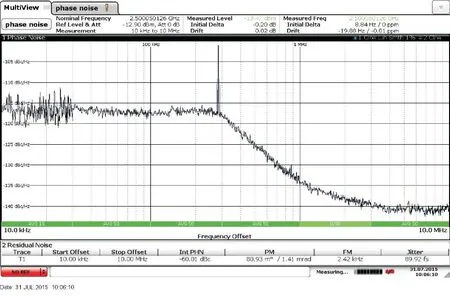
图3 HMC1035 的典型相位噪声示意图Fig.3 Typical phase noise of HMC1035

3.4 分析与讨论

受限于测量仪器的指标限制，本次实验给出的时钟抖动的积分区间为[10 kHz,10 MHz]，器件手册给出的时钟抖动指标的积分区间为[12 kHz,20 MHz]，根据测量得到的噪声功率谱密度图，可以从理论上推出积分区间[12 kHz,20 MHz]的时钟抖动[13]。

根据式（5），如图3 所示，计算得到，在[10 kHz,12 kHz]区间，噪声功率的贡献约为 6×10-9dBc 量级；在[10 MHz,20 MHz]的区间，噪声功率的贡献约为6×10-8dBc 量级。大致计算得到，在[10 kHz,10 MHz]区间，噪声功率总体为10-6dBc 量级。在[10 kHz,10 MHz]区间噪声功率基础上，减去[10 kHz,12 kHz]区间的噪声功率贡献，加上[10 MHz,20 MHz]区间的噪声功率贡献，得到[12 kHz,20 MHz]区间的时钟抖动数值。可以定量分析，[10 kHz,12 kHz]区间的噪声功率和[10 MHz,20 MHz]区间的噪声功率，相对于[10 kHz,10 MHz]区间的噪声功率小很多，理论上讲，[12 kHz,20 MHz]区间时钟抖动比[10 kHz,10 MHz]区间的时钟抖动指标稍低一些，但相差无几。

以ADS5400 为例说明超低抖动时钟在高速数据采集系统中的应用，ADS5400 孔径抖动aperture jitter 为 125 fsrms。当fin=125 MHz，ENOB=10 bits 时，根据式（2，3），得出tjrms=1.02 ps[12 kHz,20 MHz]。与tjrms相比，ADC 的孔径抖动可以忽略，HMC1035 输出采样时钟抖动亦可以忽略，此处影响ADC 有效位的因素主要为模拟输入噪声和电源纹波噪声等其他因素。当fin=125 MHz，ENOB=14 bits 时，根据式（2，3），得出tjrms=64 fs[12 kHz,20 MHz]。与tjrms相比，ADC 的孔径抖动、HMC1035 输出采样时钟抖动已经无法满足要求。当fin=1 250 MHz，ENOB=10 bits 时，根据式（2，3），得出tjrms=102 fs[12 kHz,20 MHz]，与tjrms相比，ADC 的孔径抖动、HMC1035 输出采样时钟抖动已经无法有效满足要求。同理，当fin=1 250 MHz，ENOB=14 bits 时，根据式（2，3），得出tjrms=6.4 fs[12 kHz,20 MHz]，目前所知的ADC 芯片和时钟产生电路都无法满足要求，这种情况下，可以采用下变频等方法对输入高频信号进行下变频之后采样，降低对ADC 芯片和时钟产生电路的要求。该方法在加速器的低电平控制（Low level radio frequency，LLRF）、数字移动通信等场景中应用广泛。

可以看到，针对低频输入信号、对有效位要求不高等情况时，采样时钟抖动对ADC 有效位的影响较小，甚至可以忽略，这时需要注意低噪声的模拟信号调理电路设计和电源完整性设计等。针对高频输入信号、对有效位要求高等情况时，采样时钟抖动对ADC 有效位的影响很大，需要精心设计采样时钟等以充分提高数据采集系统的模拟输入带宽和有效位。