基于联合分簇和LASSO 的室内指纹定位算法

乐燕芬，金施嘉珞，朱一鸣，施伟斌

（上海理工大学光电信息与计算机工程学院，上海，200093）

引 言

智能移动设备和无线传感器网络相关技术的融合发展，使基于位置的服务（Location⁃based servic⁃es，LBSs）如展览馆、仓库、商场等楼宇环境内的定位、导航等受到越来越多的关注［1］。如何在室内复杂的环境布局下实时获得理想的定位精度成为当前的研究热点之一。相比较基于无线信号到达角度或到达时间的定位算法，基于接收信号强度（Received signal strength，RSS）的定位方法由于只利用无线终端的信号收发功能即可实现而获得广泛的研究［2⁃4］。利用位置已知的接入点（Access point，AP）或锚节点（Anchor）来确定目标位置是其中一种方案［5⁃6］，但实际应用中，由于室内无线信号传播中存在的多径现象、斑块效应和天线方向等因素，很难有确定的信号传播模型能准确描述信号衰减量与传播距离之间的关系。因此基于无线信号地图（Radio map）的位置指纹定位算法获得了国内外学者的关注。该方法在目标监测区域内预先设立物理位置已知的参考位置点，构建反映区域无线信号分布的位置指纹库；在线定位时，通过实时接收的RSS 信号与指纹库中各参考位置的指纹进行匹配来估算目标位置。如常用的K近邻（K⁃nearest neighbor，KNN）和加权KNN（WeightedK⁃nearest neighbor，WKNN）算法，选取指纹库中与在线RSS 值欧氏距离最近的K个参考位置点，其质心或加权质心最为目标的估算位置。这一方法简单高效，易于实现，但定位精度相对不高。

基于位置指纹库的定位方法，目前很多研究工作主要集中在两方面：提高定位精度［7⁃11］和减少定位阶段的匹配复杂度来提高算法的实时性［12⁃16］。对于前者，研究的方向具有多样性。如文献［7］采用优化的WKNN 算法，首先用自适应卡尔曼滤波器对在线接收的RSS 信号进行滤波，降低环境噪声影响，同时采用Memetic 算法确定K个最近邻参考位置点的权值；文献［8⁃10］则采用机器学习的方法进行建模，其中文献［8］基于核岭回归（Kernel⁃ridge，KR）获取参考位置与RSS 信号的匹配模型，而文献［9］首先利用线性判别法对原始指纹库提取主要特征，再用这些特征值训练梯度提升决策树构建学习器进行定位。文献［10］采用深度学习中的Autoencoder，利用大量的训练样本基于极限学习机完成定位。文献［11］则通过核主成分分析法提取RSS 信号间的非线性特征，在特征空间进行指纹匹配获得估计位置。这些方法均涉及较大的计算量，提升了目标的位置估计精度。对于后者，分簇是目前研究较多的方法，如文献［12］基于信息熵对离线阶段的参考位置点进行分簇，构建接入点（Access point，AP）子集；文献［13⁃14］采用AP 聚类算法对参考位置点进行分簇。上述方法均涉及每个参考点之间RSS 信号相似度的计算，一般采用信号欧式距离的倒数作为相似度，有一定的计算量。另有部分文献［15⁃16］采用锚节点的覆盖向量对参考位置点进行分簇。具有相似覆盖向量的参考位置点归为一簇。只涉及二进制的汉明距离计算，运算简单。这些方法都基于RSS 信号特征，要求离线阶段锚节点的信号分布较稳定。聚类对定位精度最大的影响是，若在线阶段簇匹配错误，则会引入粗大定位误差。

本文所提算法的基础是分簇和机器学习，首先充分利用复杂环境下RSS 信号的分布特点，提出了基于RSS 信号覆盖向量的联合分簇方法，综合参考位置点覆盖向量的相似度和物理位置分布对参考位置点进行聚类，尽可能避免簇匹配错误；其次针对簇匹配后的二次精确定位，参考位置点RSS 样本数量少，模型容易出现过拟合的问题，引入正则项，选择简单的线性回归模型结合L1范数正则化的最小绝对值收缩和选择因子（Least absolute shrinkage and selection operator，LASSO）算法［17］获得稀疏目标解。所提出的分簇方法兼顾RSS 信号的分布特征和物理位置布局，簇内LASSO 算法在降低计算量的同时尽可能提高定位精度。

1 算法框架和设计

本文提出的基于联合分簇（Hybrid clustering，HC）和LASSO 的室内定位算法，命名为HC⁃LAS⁃SO。图1 给出了算法的框架。

定位算法分离线和在线2 个阶段。离线阶段通过采集的各参考位置点的RSS 信号确定覆盖向量，并据此完成分簇，构建多个簇指纹库；在线阶段，目标节点获取RSS 信号，根据信号的覆盖向量完成簇匹配，确定相应的簇指纹库；利用LASSO 算法，用簇指纹库拟合在线RSS 信号，确定回归系数，并以此回归系数作为权值确定目标位置。

图1 室内定位算法HC-LASSO 的框架Fig.1 Block diagram of the proposed indoor positioning system HC-LASSO

1.1 离线阶段分簇

室内复杂空间环境内有墙壁、电梯井等会严重堵塞信号，使某个区域只能接收到部分锚节点的信号。同时，锚节点也可能存在掉电、故障等原因，这样离线与在线阶段接收的RSS 信号可能并不是来自同一批锚节点，而无法实现指纹匹配。通常对未接收到的锚节点信号统一填充某个信号接收阈值，如-100 dBm 来解决这一问题。这种方法对于离线与在线阶段都适用，简单有效。为充分利用RSS 信号分布提供的位置信息，引入了指纹定位中重要的分簇概念。分簇可实现粗定位，避免在整个监测范围搜索目标节点位置而引入大计算量和大能耗，并且使最大定位误差限制在簇内。但是如果簇选择错误，则引入的定位误差将不可预测。另外基于RSS 信号特征的分簇，同一簇内的成员即参考位置点常有较分散的物理位置。这就使即使在RSS 信号匹配度高的情况下，物理位置仍可能存在大偏差。因此本文采用基于RSSI 信号特征的分簇与物理区域划分相结合的方式进行混合分簇。

图2 给出了本文实验中某个位置锚节点在定位区域的RSS信号分布。

图2 中灰色圆点是锚节点所在位置，未布置参考位置点的区域是电梯和楼梯间，也即锚节点在电梯间的墙后。可以发现由于墙壁阻挡，很多参考位置点无法接收到该锚节点信号，RSS信号分布具有较明显的区域性，而这一块区域有较相近的覆盖向量。因此可利用RSS 信号的覆盖向量作为特征进行分簇来尽可能降低粗定位误差。分簇具体过程如下。

离线采集RSS 信号构建原始指纹库Ψ，根据参考位置点能否接收到锚节点的信号，确定相应的覆盖向量Η。分别表示为

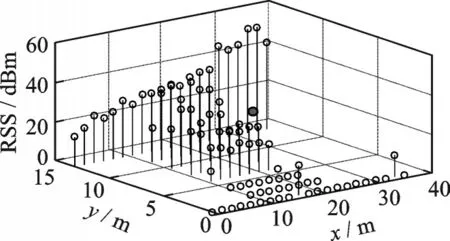
图2 某一锚节点在各参考位置点的RSS 信号强度分布Fig.2 RSS distribution in reference points from an anchor

式中：φi为第i个参考位置点Si的指纹，共N个参考位置点；φi，j为在第i个参考位置点接收到的来自第j个锚节点的RSS 信号，共M个锚节点，实际应用中，该值一般为一段时间内接收到RSS 信号的时间均值；γi为参考位置点Si的覆盖向量，一般形式为

式中j位置的向量元素1 表示在指纹采集时间内能接收到第j个锚节点的信号。反之，则表示无法接收。

分簇首先采用K中心点算法。相较于K均值算法，前者对噪声和异常点数据不敏感，虽然时间复杂度稍大，不过此分簇过程是在离线阶段，不影响在线阶段的定位实时性。按照算法，以覆盖向量为特征，计算每个参考位置点与聚类中心参考位置的汉明距离，把N个参考位置点分成K个聚类。算法过程如下：

（1）从N个参考位置中，随机选取K个，作为初始中心点；

（2）计算其余（N-K）个参考位置与K个中心点的覆盖向量的汉明距离，选取距离最小的为所属簇；

（3）任选一个参考位置R，确定其所属的簇；

（4）在该簇内，以此参考位置R为簇中心点，计算簇内所有成员与R的覆盖向量汉明距离之和作为新的距离代价函数；

（5）与原代价函数比较，若新的距离代价函数较小，则参考位置R作为该簇新的簇中心点；重复步骤（2）—（5）；

（6）若新的距离代价函数较大，则分簇完成；

（7）簇内各成员相应的指纹构成簇指纹库。

相应的原始指纹库Ψ也分为K个簇指纹库，第i个簇指纹库包含n个参考位置点，由属于该簇的位置参考点指纹构成，表示为

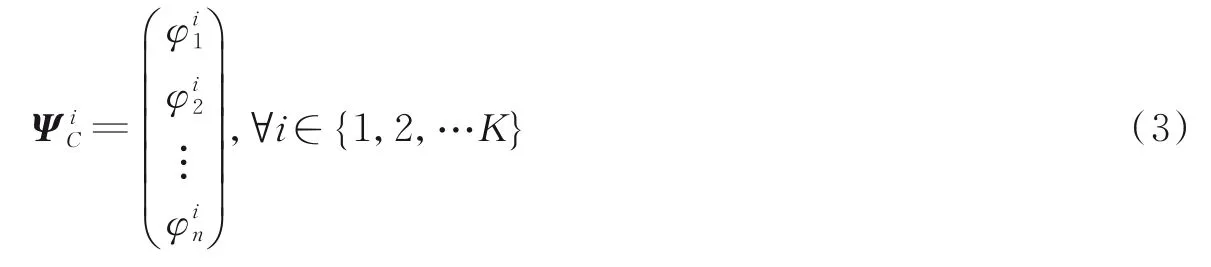
本文以聚类中心对应的参考位置点作为簇头，用于在线阶段的簇匹配。

基于物理位置的分簇则相对简单，按照参考位置点的物理地址，结合具体定位区域的空间布局特点，把指纹库相应分为L个区域指纹库，分别用表示。在线阶段的簇匹配，采用与簇内所有成员计算覆盖向量的汉明距离来完成。

1.2 在线定位

在线定位涉及2 个步骤。首先根据采集到的RSS 信号确定目标节点所属的簇，也即粗定位；其次利用定位算法完成位置估算，也称二次精确定位。

1.2.1 簇匹配

粗定位方法与分簇方法密切相关。比如离线阶段利用RSS 信号相似度进行分簇，那么粗定位时，在线RSS 信号需要与每个簇进行相似度比较。这个相似度比较可以与表征簇特征的簇头比较，也可以与簇内的每个成员比较。对于前者，簇头的选择会极大影响粗定位；对于后者则会引入相对大的计算量。本文采用覆盖向量进行分簇，簇匹配也是利用覆盖向量的相似度来完成。

在线阶段接收的RSS 信号φr表示为

相应的覆盖向量表示为γr。对于聚类产生的K个簇，采用式（5）计算在线RSS 测量值φr与第j个簇头的相似度

式中γHDj为第j个簇头的覆盖向量。选择距离最小的簇头对应的簇作为匹配簇，其指纹记为ΨCP。

对于物理分簇产生的L个簇，采用下式计算测量值φr与第l个簇的相似度

式中γZj为属于簇l的第j个参考位置点的覆盖向量，|ClZ|为第l个簇内的成员数量。同样选择距离最小的簇作为匹配簇，记为ΨZP。最终在线RSS 测量值所对应的匹配簇指纹为

式中簇内的参考位置点表示为集合ΔP。

1.2.2 簇内定位

考虑到某一时刻目标节点只能在某一确定物理空间位置，该位置可能在几个参考位置点的附近或者也可能正巧在某一参考位置点上。从信号分布的角度，可认为目标点的RSS 信号可由所选簇内若干参考位置点的RSS 信号表示。满足

式中y为在线测得的目标位置RSS 信号，ΨP为所匹配簇的指纹，ε为未知的测量误差，而θ为待定的回归系数矩阵。

定位问题就转化为θ的求解。压缩感知（Compressive sensing，CS）算法［13］把θ作为一个稀疏矩阵进行求解，即大部分元素为0。在足够稀疏的情况下式（8）的求解可转化为求解

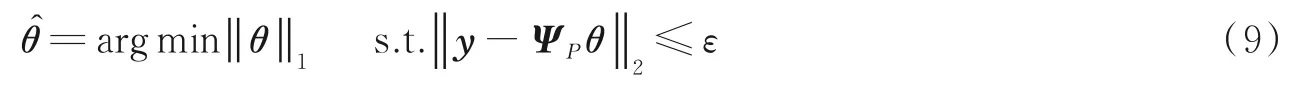
CS 算法要求ΨP指纹中各样本也即参考位置点的RSS 信号是非相关测量，否则需进行正交变换［13］，而实际应用中通常不满足这点，使CS 算法的复杂度增加。如前所述，样本之间存在相关性，使普通最小二乘法不适用回归系数θ的求解。从而引入惩罚方法来同时实现样本选择和参数估计。当惩罚函数为L1范数时，则称为LASSO，其模型为

式中t为调节系数。也即LASSO 算法在使回归系数的绝对值之和小于某个常数的条件下，使残差平方和最小。这一表达式也等价于

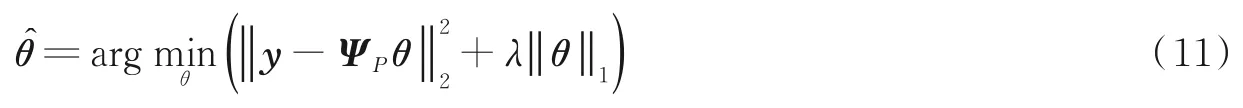
式中：λ为正则项系数，与t一一对应，用于平衡算法复杂度和拟合精度，λ越大，则惩罚程度加大，更多的系数压缩为0，从而达到特征选择或稀疏的效果。总体而言回归系数θ尽可能小，防止过拟合。

若匹配簇ΨP的指纹集合ΔP有N p个元素，此时θ是N p×1 的向量，其中有n个元素不为0，则目标位置表示为

式中Si是匹配簇内的第i个参考位置点，（xi，yi）是其相应的坐标。

从某种角度来说，目标的估计位置是不为0 的元素所对应的参考位置点坐标的加权平均。值得一提的是，线性回归模型的模型复杂度与特征维数有关。簇匹配和簇内LASSO 算法二次定位的方式，使LASSO 算法的复杂度由未分簇前原始指纹库Ψ对应的N维降低到匹配簇指纹ΨP对应的N p维，这在大监控环境下参考点分布数量较大时有利于降低算法的复杂度。

2 实验结果及分析

2.1 算法的定位精度

实验在上海理工大学光电学院9 楼办公层的大厅和走廊进行。整个无线传感器网络定位系统由锚节点、网关节点和移动节点组成，节点采用CC2430 作为主控芯片，搭载TinyOS 操作系统进行RSS 信号的采集。在两侧走廊距离地面约2.2 m 的位置共布置了18 个锚节点。在面积约为40 m×15 m 的监测区域以1.8 m 为间隔共设置90 个参考位置点。每个参考位置点采集的锚节点RSS 信号，均值化处理后构成原始位置指纹库Ψ。按照本文所提的分簇方法，图3 给出了参考位置点各自的所属簇。其中K中心点分簇法把参考位置点分为3 簇，用不同的标记表示了相应的簇；3 个虚线框分别表示了物理分簇后各参考位置点所属的簇。

在上述定位区域随机选取了21 个目标位置点，采集的RSS 信号均值化后作为在线阶段的φr，用本文所提的HC⁃LASSO 定位算法对目标进行了位置估计，并与其他几种算法进行了比较。图4 给出了各算法的误差累计分布函数。

图3 生成的簇分布Fig.3 Example of the clustering result

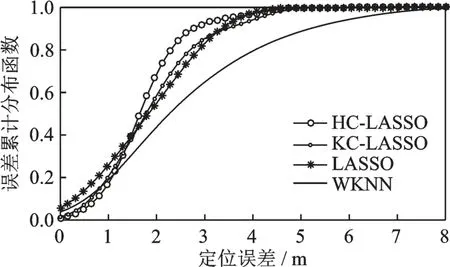
图4 HC-LASSO 算法与其他算法的定位精度比较Fig.4 CDF for HC-LASSO and other positioning methods

图4 中 HC⁃LASSO 是本文所提的联合分簇结合簇内 LASSO 定位算法，KC⁃LASSO 表示K中心分簇结合簇内 LASSO 定位算法；LASSO 表示全局采用 LASSO 算法定位［15］，WKNN 算法中K取 4，采用在线与离线RSS 信号欧氏距离的倒数作为权值。比较过程中，其他未提及的参数均保持一致。4 种算法的平均定位误差分别是：1.74，1.90，1.83 和2.58 m。而从图4 的累计误差分布图也可以看出，HC⁃LASSO 算法与KC⁃LASSO 和LASSO 比较，相对定位误差最小，说明混合分簇法能避免粗定位阶段的簇匹配错误；而LASSO 定位算法总体精度均高于WKNN 算法，说明二次精确定位阶段的LASSO 算法也具有较好的定位精度。

2.2 粗定位阶段分簇和锚节点对定位的影响

避免粗定位阶段粗大误差的关键是避免簇匹配错误，这要求离线阶段对参考位置点要有合理的分簇且在线阶段簇匹配要精确。本文研究了不同的分簇方法对定位精度的影响，结果如图5 所示。

图5 中 Kmedoids⁃LASSO、PC⁃LASSO 和K⁃means⁃LASSO 表示二次精确定位阶段均采用 LASSO算法，但离线阶段分别采用K中心点算法、物理位置和K均值算法对参考位置点进行分簇。图5 中LASSO 则表示无粗定位，直接利用LASSO 算计进行全局匹配定位。4 种算法的平均误差分别是：1.90，2.34，2.21 和1.83 m。从图中看出有几个位置点误差很大，其中第6 个位置点PC⁃LASSO 方法定位误差达到 6.87 m，而K⁃means⁃LASSO 算法有 3 个位置点误差在 4.5 m 左右，Kmedoids 有 2 个位置定位误差在4 m 左右。经分析是由于粗定位阶段簇匹配错误导致，因此本文选择了K中心点分簇和物理区域分簇结合的方式来尽可能避免粗大误差。

除了不同分簇方法会影响目标位置的粗定位，实验也对锚节点数量和分簇数量对定位精度的影响进行了分析。表1 中二次定位阶段均采用LASSO 算法，且参数保持不变。

图5 不同分簇下目标位置点的定位误差比较Fig.5 Comparison of positioning errors under differ⁃ent clustering methods

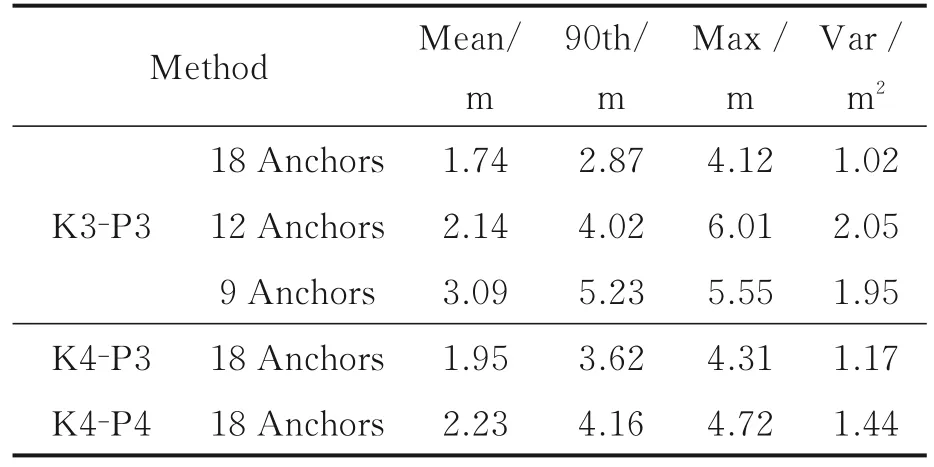
表1 不同锚节点数量和分簇数量的定位精度统计Table 1 Statistics of positioning accuracy under dif⁃ferent numbers of anchors and clusters

表1 中，K 表示采用K中心点算法，P 表示物理分簇，其后的数字表示分簇的数量，如K3⁃P3 表示采用K中心点算法把参考位置点分成3 个簇，物理分簇也是3 个簇。分析表中数据可知，当前的监测区域内，K3⁃P3 对应的定位算法精度最高。说明过多追求分簇的数量容易发生簇匹配错误，从而产生粗大定位误差。实验也研究了锚节点数量在18，12 和9 变化时定位精度的统计特性，其对WKNN 算法的影响，也具有类似的相关性。说明在分簇情况下，较多的锚节点数量更有利于准确的簇匹配。

2.3 在线阶段二次精确定位算法的选择

对于二次精确定位阶段的算法，本文对所提的LASSO 算法与 KR 算法［8］、WKNN 算法、CS 算法［13］和岭回归算法［15］进行了定位精度比较。

图6 给出了5 种定位算法的累积误差分布，同时也获得平均定位误差分别是：1.83，1.58，2.58，2.71 和 3.18 m。从图6 中也可看出核岭回归算法定位精度略高于LASSO 算法。但是考虑到核岭回归算法是训练模型来描述参考点的RSS和物理位置之间的关系，需要利用核函数来完成线性到非线性关系的转换，计算量较大，同时为获得最理想模型需要涉及正则化参数和核函数的带宽2 个参数的搜索，在分簇情况下，意味着对每个簇要分别进行参数选择。因此本文采用了计算量相对小，定位精度也较高的LASSO 算法作为二次精确定位算法。

图6 不同定位算法的误差累计分布函数Fig.6 Cumulative error distribution for dif⁃ferent positioning methods

3 结束语

基于RSS 指纹定位算法，在提高定位精度的前提下为减小在线阶段的指纹匹配量，提出一种联合分簇方法，该方法基于RSS 信号的覆盖向量采用K中心点算法对参考位置点进行分簇，同时利用物理位置对参考位置点进行划分，构建簇指纹库，融合了RSS 信号的空间分布和实际物理空间的分布特点。定位阶段利用簇匹配完成目标的粗定位，在小样本的前提下，采用LASSO 算法完成目标位置的二次精确估计。本文从不同分簇方法、分簇数量、锚节点数量等方面对算法进行了分析，并与其他室内定位算法进行了对比。实验结果表明，本文所提的定位算法通过合理的分簇，在降低在线匹配计算量的同时能保持良好的定位效果。更大规模区域的算法应用及实时在线定位系统的实现是下一步的研究目标。