收敛数列性质的可视化

刘艳　郑慕聪

摘 要 基于数列极限的严格定义，给出数列极限可视化的几何解释，用可视化的几何解释简洁直观地分析和证明收敛数列的三个基本性质。通过可视化的方法让学生感受数列极限定义的精髓，并且更加直观的理解收敛数列的基本性质。

关键词 高等数学 数列极限 收敛 可视化

中图分类号：O171文献标识码：A

0引言

高等数学是以微积分为主要内容，结构严谨，概念抽象，内容深刻，系统性强。基本概念是知识体系的基础，它往往体现了重要的数学思想，却又很抽象。以极限为工具的基本概念和基本方法演绎形成结构严谨内容深刻的这一套现代数学知识体系对学生的抽象思维能力和逻辑推理能力要求高，这让许多刚进大学数学课堂的学生很难适应。特别是，数学语言“”描述的数列极限的概念学生很难理解，由数列极限的定义得到收敛数列的基本性质学生更是难以掌握。如何让学生更好地理解数列极限的概念和收敛数列的性质，这是教师要解决的关键问题。本文从全新的角度，通过可视化的方法让学生感受数列极限定义的精髓，并且用可视化的方法让学生更加直观的理解收敛数列的基本性质。

1数列极限的定义及可视化

众所周知，微积分是由牛顿和莱布尼茨独立创立的。在当时，微积分的理论基础并不完善，特别是没有给无穷小准确的定义，牛顿所谓的无穷小被当时的大主教贝克莱抨击为“幽灵”。后来经过欧拉、达朗贝尔等几代数学家共同努力下，柯西给出了极限概念的准确描述，最终由维尔斯特拉斯给出“”、“”的严格定义。极限严格的定义是数学家们经过100多年的努力最终给出的，学生一开始难以理解是正常的。极限作为高等数学的基本工具是非常重要的概念，教师的任务就是让学生在能够接受的范围内更好更清晰的理解这一核心概念。

定义1：设为一数列，若存在常数，对于任意给定的正数，总存在一个正整数，使得当时，都有，则称是数列的极限或称收敛于。记

或

如果一个数列有极限，就称这个数列是收敛的，否则称它为发散的。

对于数列极限这一概念，学生都可以朴素的理解为：随着无限增大，与无限接近，想要多接近就有多接近。数学的概念都是由精确的数学语言来刻画，对于定义1中抽象的数学符号以及表达式的含义需要给学生清晰的解释。

首先将定义1用更简洁的数学语言来表达

， ，当时有   （1）

事实上，我们可以将数列看作是一个离散变量的函数，

，，                                                  （2）

那么 表达了这个函数的一个变化过程：随着自变量不断变大，朝X轴的正向趋向于无穷，因变量即函数值无限趋向于。这时数列在直角坐标系下的图像就可以直观的反映出来。

观察（1）式，用绝对值来刻画的接近程度。如何表达与想要多接近就有多接近，达到无限接近的程度呢？这时的任意性的价值就体现出来，无论给定有多小，都比还要小。而“”，当不等式成立正好反映了这个函数的变化过程，通常来说，这里的是依赖于的，取得越小，所找到的一般就越大。后面的可视化内容会反映这一点的。只要满足存在性即可，它不是唯一的，也不需要满足唯一性，也就是说一旦给定一个具体的，就能找到一个相应的。事实上，只要存在一个相应的，那么所有比大的正整数都可以满足不等式。

当然，为了让学生更直观的理解上述内容，我们接下来需要将相关概念通过动态图像表达出来。由于即即，也就是说落入到的邻域。从函数的角度看待，它是一个带状区域。由于的任意性，所以带状区域的宽度可以任意收缩。用PPT动画展示带状区域收缩的变化过程，如图1、图2所示，并指出无论多小，总存在相应的，项以后的所有项都落入带状区域内。

最后，我们给出一个具体的例子的图像说明的关系，如图3、图4所示，得到该数列极限的直观的几何解释。

2收敛数列性质的可视化

收敛数列具有三个基本性质：极限的唯一性、收敛数列的有界性和收敛数列保号性。理解这些性质并且能够从收敛数列的定义出发来认识这些性质对理解极限是微积分的基本工具有着重要意义，这种逻辑推理的思想和方法一直贯穿于课程始终。下面我们通过定义1的可视化几何解释来说明这三个基本性质。

定理1：如果数列收敛，那么它的极限唯一。

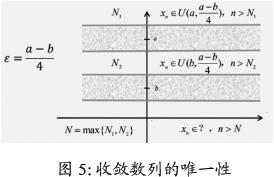
对于学生来说，这个结论显而易见，很好理解。可是被问到为什么唯一，学生第一反应也许是怎么可能不唯一！接下来自然会想到如果不唯一那么就会有矛盾。如何寻找矛盾，这时就必须回到数列收敛概念本身。如果收敛到两个不同的值（不妨设），那么由定义1的几何解释，根据的任意性，取，通过PPT動态展示就会得到如下图5所示的情形。

图5中，项以后的所有项既要进入上面的带状区域又要进入下面的带状区域，这显然是个矛盾。在这种直观的推理解释下，学生对于极限概念和唯一性的认识就有了更为深刻的印象。

定理2：如果数列收敛，那么一定是有界的。

证明有界，就是要证明存在某个正数，对，。还是回到定义1的几何解释，由的任意性，取，就会得到如下图6所示的情形。对于，我们可以找到相应的，项以后的所有项进入到图6中的带状区域，这显然是有界的。前项是有限项，显然也是有界的。于是就找了图6中的，对，。这就说明有界。

定理3：如果，且（或） ，那么存在正整数，当时都有（或）。

定理3刻画了收敛数列的保号性。保号性对于学生来说是一个新概念，所谓保号性就是收敛数列的极限的正负可以保证数列从某项开始以后无穷多项的正负。从具体的收敛数列的图像（图3、图4）来看是显而易见的。如何从条件，且 出发得出结论呢？我们依然回到定义1的几何解释，由的任意性，取，就得到如下图7所示的情形

对于，我们可以找到相应的，项以后的所有项进入到图7中的带状区域，由于带状区域在X轴上方，所以当时都有。对于时的情形如图8所示，不难得出相应的结论。

3总结

数列极限的“”的严格定义中的任意性是定义的灵魂，它保证了与极限可以无限接近。把数列看作离散变量的函数，从函数图像的角度给出数列极限的几何解释可以更直观的反映出的关系。基于的任意性，选取合适的值，由数列极限可视化的几何解释不难得到收敛数列的基本性质：极限的唯一性、收敛数列的有界性和保号性。

高等数学课程是大学理工科专业的基础课程，具有概念抽象，结构严谨，系统性强的特点。极限是高等数学中的基本工具，理解和掌握极限概念对学生学好这门课程起着至关重要的作用。本文提出的可视化的方法让學生更加直观的理解数列极限的概念和收敛数列的性质。当然这只是高等数学课程的开始，如何将抽象的数学理论和方法用可视化的方法或者生动形象的例子展现在课堂上，让学生更好的学，并且激发学生思维的火花将是我们下一步教学研究与改革的方向。

基金项目：陕西师范大学教学改革研究重点项目（17GGK-JG03）;西安科技大学教育教学改革与研究项目（JG18069）。

作者简介：刘艳（1978.9-），女，汉族，陕西兴平人，西安科技大学理学院讲师，硕士，主要研究领域为智能信息处理;郑慕聪（1981.2-），男，汉族，湖北老河口人，陕西师范大学数学与信息科学学院讲师，博士，主要研究领域模糊推理与决策、数学教育教学。

参考文献

[1] 韩雪涛.数学悖论与三次数学危机[M].北京：人民邮电出版社，2016.

[2] Victor J.Katz.数学史通论（第2版）[M].李文林，邹建成，胥鸣伟等译.北京：高等教育出版社，2004.

[3] 同济大学数学系.高等数学（第7版）[M].北京：高等教育出版社，2014.