运用加权TOPSIS 法的学术期刊影响力的定性与定量评价研究
2020-12-17王慧喻琨
●王 慧 喻 琨
随着我国步入新媒体时代,学术期刊的传播途径趋于多样化。因此,衡量一篇学术期刊的影响力,不单单只看传统引文这一单一指标,应将新媒体这一项指标纳入到学术期刊影响力评价体系内。那么,在当前研究成果的基础上学术期刊影响力综合评价体系构建时主要包括哪些新媒体的指标?权重多大?这是本文需要重点解决的问题。本文基于TOPSIS 理论,来对湖南省学术期刊的影响力进行评价,从而确保这一模型方法使期刊评价工作既能便捷有序地进行,又能使评价结果客观公正,并在实践中具有指导价值。
一、基于TOPSIS 的学术期刊影响力理论框架
(一)学术期刊影响力概念
学术期刊是学术研究成果重要体现,学术期刊是推动学术发展与创新的不竭动力。学术期刊的影响力体现的是在一定期间内在某一期刊上发表的学术研究成果,为当前相关研究与应用的发展所提供的贡献力。学术期刊的影响力本质来源于所承载文献的研究价值与应用价值,但其影响力也受到其他相关因素的限制,如该期刊自身传播途径与方式、社会对于该期刊的认知程度以及该期刊的内容是否具有多元化特征。通过定性评价与定量评价方式对学术期刊的影响力进行评价,能够较大程度上提升学术期刊的水平,保障期刊的稳定发展。
(二)学术期刊影响力评价现状
1.定性评价。就当前定性评价方法而言,期刊影响力最基础的评价方法是同行评议。同行评议一般是通过业界内的权威专家对期刊根据不同等级进行分级排序,从而对学术期刊的影响力有一个直观的评价。该方法的优点在于易操作,但缺点也十分突出,耗费大量的人力与物力成本,更关键的一点在于,受主观因素的影响较大,定性评价容易受到学术偏见、人情分、个人理解与见解的差异等因素的影响。因此往往会产生不同专家的评审结果差异十分大的情况出现。
2.定量评价。定量评价主要是通过对期刊文献的计量进行统计分析,以此作为期刊影响力评价的重要指标。其中单指标评价与多指标综合评价是当前学术期刊影响力定量评价的两种方法。
一是单指标评价。指的是通过单一的指标对学术期刊的影响力进行评价,国外的研究表明对于期刊的影响力较大的因素主要有年下载率、文献转载率、H 指数、SJR 指数等。随着信息技术对科研环境的影响,由此诞生出例如Altmetric 等的补充计量指标。为了使评价结果更加科学客观,一些优秀的学者也在不断挖掘新的文献计量指标。有的学者是在已有的成果基础上进行完善,如熊晓英(2005)提出将影响因子同相同期刊的平均影响因子作对比,证明了影响因子适用于不同学科期刊的比较研究①,但该指标依然受期刊不正当自引、批判性引用等因素的影响。邵作运(2015)提出了一种新的期刊影响力评价指标——f(x)指数,综合考虑了期刊的载文量、被引量、篇均被引等因素,以及低被引和高被引论文的差异性,但f(x)指数默认所有引文具有同样的权重,没有排除自引现象对评价结果的干扰②。
二是多指标综合评价。该评价方法是从不同角度、不同层面来构建期刊影响力评价方法,通过统计学方法对指标体系进行综合得分计算。常用的方法有层次分析法、模糊评价法、德菲尔法等。如王建军③选取影响因子、5 年影响因子、即年指数、被引半衰期、他引率、H 指数、Web 即年下载量和基金论文比8 项指标,利用层次分析法对管理学期刊的学术影响力进行综合评价.马虎兆④选取期刊载文量、影响因子、他引总引比、被引半衰期、H指数、即年指标和Web 即年下载率7 项指标,利用层次分析法确定指标权重,最后通过乘法模型计算各指标的综合得分,等等。
(三)基于TOPSIS 的学术期刊影响力内涵
TOPSIS 法是一种常用的综合评价方法,主要是通过对所统计的数据信息进行利用,其最终计算出的结果便能够充分反映出对学术期刊的不同评价方案之间的差异性⑤。其原理是以原始数据矩阵为基础,通过余弦法找到评价方案中的最优项与最劣项,最后根据所评价的对象来决定最优项是否合适,通过该种方法来评价学术期刊的影响力。TOPSIS 主要是根据数据的样本分布来分析,对它的次数没有严格的限制,其优点在于操作简单,容易计算。
(四)基于TOPSIS 的学术期刊影响力评价指标体系
通过对学术期刊能力的影响因素进行分析,基于TOPSIS 评价方法构建出学术期刊影响力的评价指标体系。主要从文献引用分析、新媒体环境、期刊自身发展、基础指标作为一级指标,通过TOPSIS 数学模型来对湖南省学术期刊的影响力因素及湖南省学术期刊的能力水平进行分析,找到影响期刊能力的关键因素,为今后学术期刊的发展提出参考性建议。同时通过对各类学术期刊进行综合评价,为学术期刊找寻准确定位。
二、指标的选取与计算步骤
(一)指标选取
指标选取,要兼顾两方面:一方面,看指标体系能否体现出期刊质量评价发展状态及可持续性特点;另一方面,要看指标是否具备明确的概念,较强的可操作性,若为定量指标,则看是否可度量,若为定性指标,则评价模糊度量能否实现。本文对国内外和期刊质量评价有关的研究进行了搜集整理,最终确定湖南经济管理类期刊质量测评体系,包括一级指标有3 个,二级指标有14 个,从表1 可以看到指标明细。
1.基于引文分析的指标:传统引文分析指标在学术期刊评价工作的发展中已日趋成熟,目前国内外几大权威评价机构所使用的评价指标均为引文分析指标。基于引文分析的指标归纳为6项。
2.基于新媒体环境下的指标:随着新媒体时代的发展,使用网络平台进行学术交流的用户越来越多,利用网络平台进行学术传播也远比纸质媒介传播快得多。本文选择百度指数、微信公众号、新浪微博、万维期刊网以及期刊官网几大平台构建网络指标加入期刊评价的研究,扩展目前基于传统引文分析的指标体系。
3.基于期刊自身发展的指标:基于期刊自身发展的指标由于难以取舍和衡量,且数据值不易量化,较少被人使用。本文基于期刊在创刊办刊、选文编辑、出版发行的过程中所形成的特色,选取创办时间、获奖次数、被重要检索收录、网站建设度为评价指标。
具体指标体系构建如表1 所示。

表1 新媒体环境下的指标和期刊发展指标来源参考
(二)TOPSIS 法评价模型构建的步骤
1.首先建立评价矩阵。有n 个需要进行评价的对象,p 个评价指标,使他们构成一个n×p 的矩阵,如果评价指标中有逆指标,我们需要将其进行正向化处理,最终得到的矩阵如下:

其中:zij=gij×ωij,i=1,2,…,n;j=1,2,…,p;
ωij为第j 个指标的权重
4. 由各项指标最优值和最劣值分别构成最优值向量Z+和最劣值向量Z-。
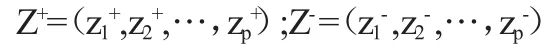
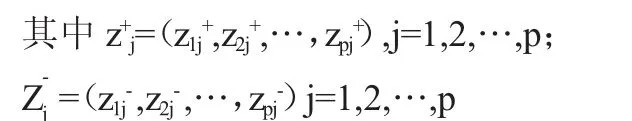
5.计算各评价单元与最优值和最劣值的距离。
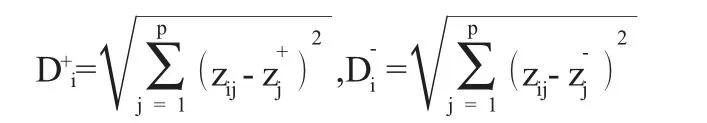
6.计算各评价单元与最优值的相对接近度。
通过正理想解来表示最优解,负理想解表示最劣解,其中正理想解对应于各指标的最大值集合,负理想解对应于各指标的最小值集合。正理想解计算公式为X+j=maxiCij,负理想解计算公式为X-j=miniCij,其中j=1,2,…,m。⑥
假定各参评对象与正理想解之间的距离为D+i,与负理想解之间的距离为D-i。对方案和理想解距离(贴近度)进行计算,即

较大的贴近度意味着此参评对象和理想解拥有极高的贴近度,即非常贴近理想解。就此而言,贴近度高低能够对不同参评对象进行优劣排序。
7.依据接近度数值的大小进行排序,Ci越大,表明第i 个评价单元越接近最优水平。根据Ci大小降序排列,获得湖南省5 种经济管理期刊影响力排名。⑦
8.分别对数据进行权重赋值。一般情况下考虑到这些指标的本身需要和算法的特性,所以赋值的权重相同。
(三)湖南5 种经济管理期刊质量评价实证研究
本文以湖南省5 种经济管理期刊作为研究对象(见表2)。从经济管理期刊办刊现实情况出发,由12 名编辑学相关专业的专家学者确定表1 评价指标的数值,[0,1]为数值确定依据,取小数点后三位。在算术平均法的支撑下,对5 种经济管理期刊的不同指标初始值进行整理核算,由式(1)可将表2 绘制出来。

表2 湖南5 种经济管理期刊质量评价指标数值
以式(2)和式(3)统一处理原始数据,借助于式(4)对不同指标权重进行计算,具体见表1。
利用标准化矩阵R 和表1 得到的评价指标权重得出加权值C 见表3。
根据公式计算正、负理想解,并计算5 个被评价对象距离正、负理想解的差异。详情可参看表4。
计算5 种经济管理期刊质量与理想解的贴近度:
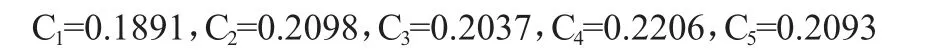
排序为C4>C5>C2>C3>C1
在综合评价5 种经济管理期刊后发现,《经济地理》拥有最佳的期刊质量评价品质,《企业家天地》拥有较差的期刊质量评价品质。
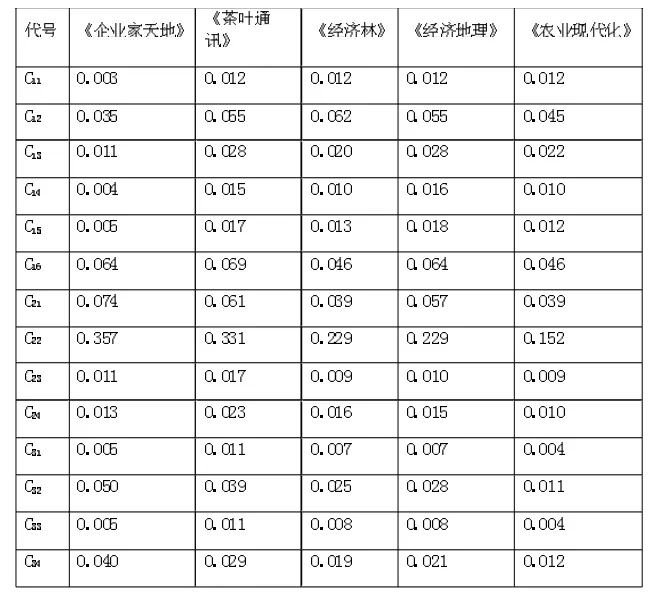
表3 湖南5 种经济管理期刊景观评价指标加权值
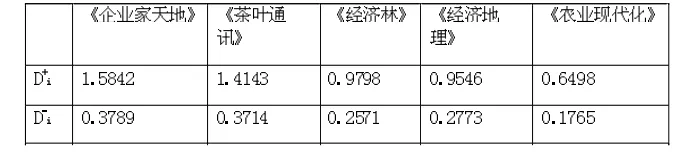
表4 5 种经济管理期刊质量和正/负理想解的差异
总之,本文以TOPSIS 模型为指引,为期刊质量评价指标体系在国内的构建,进行了指标筛选方面的探索。开展后续研究的时候,借助于问卷调研方式,深刻探究指标信度和效度,有助于对期刊质量评价进行规范,让期刊质量评价变得更加有效。
注释:
①熊晓英. 相对影响因子及其意义[J]. 中国科技期刊研究,2005,16(06):912- 914
②邵作运,李秀霞.f(x)指数:期刊学术影响力评价新指标[J].中国科技期刊研究,2015,26(11):1194- 1199
③王建军,杨德礼.管理学CSSCI 检索期刊学术影响力分析[J].情报学报,2010,29(01):142- 150
④马虎兆,于挨福.基于乘法模型和层次分析法的科技期刊学术影响力评价研究——以科学研究类期刊为例[J].情报杂志,2009,28(6):101- 104
⑤曾琳, 蒋平. 地方普通高校大学生创新创业政策导向与路径探析[J].西南师范大学学报(自然科学版),2019,44(08):110- 116
⑥胡列格,李佩,徐其昌.基于TOPSIS 法的公交线网布局方案评价方法研究[J].公路与汽运,2011(03):40- 43
⑦刘江婷,陈岩.基于区间直觉模糊数Choquet 积分算子的TOPSIS方法[J].曲阜师范大学学报(自然科学版),2019,45(03):35- 41
