基于模糊控制的虚拟服务器暴露时间的确定

2020-12-17秦振翔马润年

空军工程大学学报 2020年5期

秦振翔, 马润年

(空军工程大学信息与导航学院，西安，710077)

近些年来，先进可持续性威胁(Advanced Persistent Threat,APT)的发展使网络安全的形势越来越严峻。传统防御网络所特有的确定性、相似性、静态性及漏洞的持续性是现有网络信息系统的致命安全缺陷[1]。这些缺陷将直接导致网络信息系统始终处于被动挨打的局面。因此，完善防卫系统的防御强度就十分必要。然而，无论防御强度有多高，只要主机处于静止状态，攻击者总有办法通过时间成本来换取攻击效益。移动目标防御就是设法打破这种静止状态，从而可以增加攻击成本，使攻击者得不偿失。目前，在对移动目标防御中软件层、平台层、网络层和数据层进行的相关研究中，前人已取得了不少成果。

平台层的移动目标防御通过构建多样化的运行平台，进而动态改变其运行环境，缩短应用在某平台上的暴露时间。文献[3]应用了相关Web服务多样化技术，提出了虚拟服务器软件栈的设计方案，却未进一步对虚拟服务器的最大可暴露时间做定量分析；文献[4]利用多样化的软件栈模板，设计了基于异构平台的虚拟服务器池，未对虚拟服务器的最大可暴露时间进行定量分析；文献[5]在平台暴露时间和随机迁移次序等因素影响下，提出了3种面向隔离区的主动迁移策略，未进一步对迁移时间做定量分析；文献[6]基于前人移动目标防御的研究成果，进行了分类与总结，不需要定量分析虚拟服务器的最大可暴露时间；文献[7]对动态平台技术作为防御机制进行了定量评估，没有进一步分析虚拟服务器的最大可暴露时间；文献[8]基于云计算对Web防御系统进行了相关的研究，不需要对虚拟服务器的最大可暴露时间进行定量分析；文献[9]针对传统 Web 服务可信性难以适应动态评估的问题, 提出了一种基于信息熵权重和带修正指标的动态信任评估模型(Dynamic Trustworthy Evaluation based on Information Entropy and Correction Metrics,DTEIECM)，不需要对虚拟服务器的最大可暴露时间进行定量分析；文献[10]针对传统网络的静态等特性，提出了一种软件定义APT攻击移动防御网络架构(Software Defined Moving Target Defense Ar-chitecture, SDMTDA)，不需要对虚拟服务器的最大可暴露时间进行定量分析；文献[11]针对端信息跳变的有关问题，提出了一种基于非广延熵和Sibson 熵融合的实时网络异常度量算法，不需要对虚拟服务器的最大可暴露时间进行定量分析。而这些都未定量地对防御平台中虚拟服务器的最大可暴露时间进行分析。

不同的虚拟服务器在平台上的暴露时间会有所不同，可能是因为各服务器中的被攻击面不同。目前，很少有文献在保证系统不被攻破的前提下对服务器的最大可暴露时间进行定量的研究。本文假设防御者清楚状态攻击面，且攻击者不能在某个时间段内攻破。那么，保证系统虚拟服务器安全的时间至少大于系统虚拟服务器的最大可暴露时间。因此本文试图基于模糊控制相关理论与技术，以攻击面的度量结果和漏洞评估结果为输入，最终输出服务器的最大可暴露时间，达到保证系统虚拟服务器不被攻破的目的。

1 模型描述

如图1，基于模糊控制技术，对受到攻击的虚拟服务器进行相关攻击信息的采集，分析后得到攻击面数学期望，再根据国家信息安全漏洞库(China National Vulnerability Database of Information Security, CNNVD)中的漏洞分级规范对系统漏洞进行评估，得到一个评估分数，再将这2个指标输入到模糊控制器中，得到该服务器最大暴露时间。再将暴露时间反馈到控制程序，作为确定切换到下一个服务器时间点的参考依据。

图1 基于模糊控制确定平台暴露时间体系结构

虚拟服务器一般由4个部分组成，每一个部分都有具体的构成形式，Web服务多样化即是让各部分的具体构成形式在兼容模式下进行任意组合。

1.1 攻击面定量分析

攻击面是攻击者进入被攻击系统的“桥梁”。一般来说，攻击者可以通过一些系统的内部程序、系统通道(如套接字)等和系统中共享的数据项来对目标系统发起攻击。这些资源在系统中某一时刻存在的可被攻击点统称为攻击面[11]。在此，可以用Nessus对Web虚拟服务器进行漏洞扫描，将漏洞作为攻击面。

为了方便研究，设定9个虚拟服务器。每个虚拟服务器均有3种模式，即在线模式、关闭模式和离线模式。在线模式下，接受攻击并收集攻击者信息；关闭模式下，将收集到的攻击信息进行分析；离线模式下，对存储的攻击信息进行清零操作，为再次收集做好准备。

设Ai表示虚拟服务器i的在线模式,i=1,2,…,9。假定9个虚拟服务器只有一个处于在线模式，并且假设在平稳状态下虚拟服务器i处于在线模式的概率为xi，各个虚拟服务器的模式切换符合马尔科夫链。规定服务器在完成切换的同时，在线模式会自动转变成关闭模式，最后变成离线模式。设状态Ai转移到状态Aj的转移概率(各虚拟服务器间的切换概率)为pij，可得此系统状态转移矩阵为：

(1)

设各个状态间转移时间的间隔相等均为Δt∈[0,1]，随机化程度R∈[0,1]，防御者对攻击者探测报文的拦截率t∈[0,1]，pdi是攻击者探测到漏洞的概率，满足以下函数关系：

式中：T0表示为扫描到该虚拟服务器中所有攻击面(在此指漏洞)所需时间的最大值。

本文假设防御者清楚状态攻击面，且攻击者不能在某个时间段内攻破。在状态空间A={A1，A2，…，A9}中，我们任意设定其中的状态转移(服务器切换)规则为：若转移前它在A2，A3，…，A8,则它分别以1/3的概率向前、向后转移或者保留原处；若转移前，它在A1，则它以概率1转移到A2；若转移前，它在A9，则它以概率1转移到A8。由此可得此系统的状态转移(服务器切换)概率矩阵为：

(2)

由马尔科夫链的相关基础知识可得：平稳状态X=(x1,x2,…,x9)可根据X=Xp可得：

(3)

解得：X=(1/23, 3/23,3/23,3/23,3/23,3/23,3/23,3/23,1/23)

不管初始状态什么样，系统在经过转移后，达到一个马尔科夫平衡状态。据此，可算出攻击面的数学期望值：

(4)

式中：ki表示第i个虚拟服务器中的可被攻击点的个数，在此为Nessus扫描到的漏洞个数。

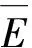
1.2 操作系统漏洞评估

本文基于CNNVD漏洞分级规范来对Nessus扫描到的线上虚拟服务器的漏洞进行相关评估。凡是被CNNVD收录的漏洞，均适用此分级规范，包括采集的公开漏洞以及收录的未公开漏洞，通用型漏洞及事件型漏洞[14]。该项评估主要基于可利用性指标组和影响性指标组来对其进行定量评估。

如表1、表2所示，根据以下7种指标来对系统漏洞进行评估，再根据CNNVD分级规范给定的评分表，即可得出2组指标的评分。2组指标的评分和为评估结果。如：攻击途径为网络、攻击复杂度低、无权限要求和不需要用户交互的情况下，可用性指标组评分为3.89；在高机密性影响、高完整性影响和高可用性影响的情况下，影响性指标组评分为5.87。因此2组评分和9.76即为最终的评分结果。

表1 可攻击性指标

表2 影响性指标

2 模糊控制系统

在目前的平台层的移动目标防御研究中，很少有对服务器最大可暴露时间做出相关定量研究。因此，本文试图运用模糊控制系统在仿真环境中对服务器可暴露时间做出定量分析。

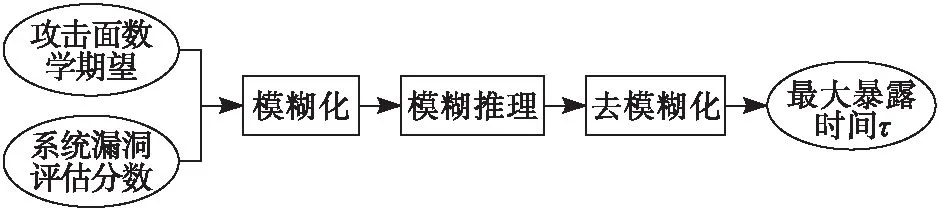
图2 模糊控制原理框图

2.1 模糊化

在模糊控制系统中，为方便研究，将2个输入量分别模糊化成3个子集、输出量模糊化成5个子集，再选取三角形隶属函数。

1)对于攻击面数学期望，选定3个模糊子集：期望值小(ES)、期望值中(EM)、期望值大(EL)。为研究方便，假设输入x的定义域为[0,6]，则可得其隶属函数:

(5)

2)对于系统漏洞评估分数，选定3个模糊子集：分数低(SS)、分数中(SM)、分数高(SL)。根据CNNVD的分级标准，可得评估分数在[0,10]内，大于10的以10来代替。因此，输入y的定义域为[0,10]，则可得其隶属函数:

(6)

3)对于输出量即服务器可暴露时间，选定5个模糊子集：很短(SV)、短(S)、中等(M)、长(L)、很长(LV)。为研究方便，假设输出τ的值域为[0,12]，以min为时间单位，可得其隶属函数如下:

(7)

2.2 模糊推理

根据已有的攻防先验知识，系统越危险，在保证系统不被攻破的前提下，虚拟服务器完成切换越快，其暴露时间就会越短。因此，切换要尽快完成。据此有以下模糊规则：

1)攻击面数学期望越大，漏洞评估分数越高，服务器可暴露时间就越短；

2)攻击面数学期望适中，漏洞评估分数适中，服务器可暴露时间就适中；

3)攻击面数学期望越小，漏洞评估分数越低，服务器可暴露时间就越长。

在此，假设漏洞评估分数对服务器可暴露时间影响更大且更显著。对攻击面数学期望和漏洞评估分数各3种情况进行组合，可得到具体的模糊规则，见表3。

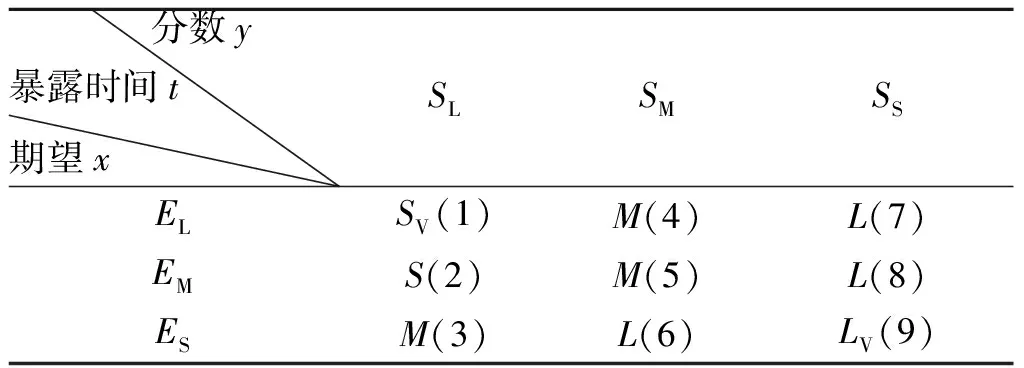
表3 模糊控制的具体规则表

2.3 去模糊化

根据以上的模糊规则，在理想状态下，总的集合应由上述所有的规则进行并集运算得到。然而在一般情况下，由于每次的输入量不可能全部激活上述规则，因此根据这一特点，只取出激活了的规则相并作为研究对象即可，再进行近似推理。最后通过最大隶属度的最小值法得到平台暴露时间，完成系统输出的去模糊化。

3 仿真分析

3.1 仿真环境及参数设置

首先利用Nessus对在线模式下的虚拟服务器进行漏洞扫描，并记录下漏洞数量为ki，再利用国家信息安全漏洞库中的漏洞分级规范逐一对漏洞进行定量评估。表4为Web虚拟服务器构成。

表4 Web虚拟服务器构成

按照表4，构造出9种不同的虚拟服务器后，逐一对在线模式下的虚拟服务器的攻击面进行计量，同时对软件栈中的漏洞进行评估。再将2个数据输入到Matlab中的Fuzzy logic designer，经过仿真即可得到平台暴露时间。

在Matlab中找到Fuzzy logic designer的应用程序，首先添加一个输入量并对两输入进行重命名，再确定其各自的Range。分别对输入/输出量进行双击，按照上文既定的隶属度函数进行设置，编译模糊规则,最终得到仿真结果。

3.2 仿真结果分析

在仿真中，在攻击面数学期望和漏洞评估分数的区间内，任意给定一组数据，可得到服务器的最大可暴露时间。如图3所示，给定77组数据，绘制成三维散点图。根据图中点的分布情况，不难发现漏洞评估分数对虚拟服务器暴露时间的影响确实大于攻击面数学期望的影响，攻击面数学期望越大，漏洞评估分数越高，在尽量保证虚拟服务器不被攻破的情况下，最大可暴露时间越短。