SC-FDE系统中基于压缩感知的慢衰落航空稀疏信道估计

毕号旗，向 新，李 娜，郑万泽，鞠 明

(1.空军工程大学航空工程学院，西安，710038；2.西安电子科技大学通信工程学院，西安，710071；3.空军工程大学科研学术处，西安，710051；4.91313部队，北京，100038)

航空无线信号在传输过程中受到地理环境以及收发机相对运动的影响，其传输信道存在延迟扩展、多径衰落和多普勒频移。同时航空无线传输多强调移动和障碍物阴影衰落的影响，通常建模为具有慢衰落特性的多径信道，即信道响应的变化通常大于传输符号时间。

实测信道[1-2]表明，航空多径信道是一种稀疏信道，即：信道的单位冲击响应系数分散在个别抽头，其余抽头权值为零。通过航空信道的码元之间相互影响，当前码元可以影响其后数十个码元，引起严重的码间串扰(Inter Symbol Interference，ISI)，导致通信质量下降。此时，可以通过单载波频域均衡或者采用OFDM等技术消除信道对信号的影响。但是OFDM存在对频偏敏感、峰均比高的问题，而分块传输的单载波频域均衡(Single Carrier Frequency Domain Equalization，SC-FDE)技术实现较为简单且在航空机载应用环境中使用较佳，因此得到广泛应用[3]。

SC-FDE系统依赖于准确的信道估计，否则会传递误差，导致输出误码率高[4]。目前，信道估计的方法可以分为2类：①借助导频信号估计信道，牺牲带宽换取稳定性；②根据发射信号的统计特性对信道进行盲估计[5]，虽然省去了导频的开销，但是复杂度高。借助导频信号进行信道估计有2种方法：①根据最小二乘(Least Squares，LS)准则进行估计，包括时域和频域估计方法。最小二乘方法对于密集分布的无线信道估计是最优的，当传输信道是稀疏信道时，估计性能下降[6]。②利用伪随机序列(Pseudo-Noise Sequence，PN)的循环相关特性进行估计[7]，复杂度低，但由于序列相关性不理想，存在残留矩阵，导致信道估计精度低于最小二乘方法。以上2种方法主要应用在抽头能量分布密集的信道估计上，没有利用稀疏信道的特点，估计效率不高。在OFDM系统中，经常采用效率较高的压缩感知方法进行稀疏信道估计[8-9]：根据信道的稀疏特征和OFDM系统模型构造测量矩阵，通过恢复算法重建信道响应。由于系统结构不同，OFDM系统中压缩感知估计信道的方法不能直接应用于SC-FDE系统。

因此，为解决SC-FDE系统中航空稀疏多径信道估计不准确影响后续信号处理的问题，本文拟针对航空慢衰落多径信道系数特性，提出一种基于压缩感知框架，利用PN序列构建优化测量矩阵，采用SAMP算法作为恢复算法的航空多径稀疏信道估计算法——PN-SAMP算法，并与PN算法、LS算法和OMP算法进行了比较。

1 单载波频域均衡系统

在发射端，待发送的连续比特流被映射成离散符号并用矢量表示，实现正交调制，同时添加循环前缀完成数据块的构建。在数据块前面添加导频块，得到完整传输帧结构，如图1所示。传输帧成形滤波器变为连续波，再由载波调制发射出去。在接收端，利用滑动相关器对导频信号进行定位，去除CP，提取导频用于信道估计。将数据块部分通过FFT变换到频域完成信道均衡，随后通过IFFT变换回时域，完成信号的判决和输出。图2为单载波频域均衡系统结构图。

图1 传输帧结构

图2 单载波频域均衡系统

根据MMSE频域均衡的原理，得到均衡器的频域表达式[6]：

(4)

式中：“*”表示共轭；N0为噪声功率谱；H为信道的频域表达式。

在频域完成均衡后通过IFFT将频域均衡器输出变换回时域，得到软判决输出：

z=FHCY

(5)

式中：Y为接收信号的频域向量；FH为F的共轭转置矩阵，表示IFFT运算。

最终，根据最大后验概率准则(Maximum A Posteriori Estimation，MAP)对均衡器输出的时域信号z进行硬判决，得到星座输出:

(6)

式中：dec(·)表示信号硬判决输出。

2 利用压缩感知估计航空稀疏信道

2.1 航空多径信道的稀疏性

一般来说，不同的飞行场景对应不同的信道模型，按照地理环境进行建模虽然准确但是复杂度高，且模型可移植性不强。因此，一般依据广义平稳非相关散射(Wide-Sense Stationary Uncorrelated Scattering，WSSUS)准则，通过统计的方式对时变多径信道建模[10]。本文主要关心巡航状态下的航空信道模型。

飞机巡航场景如图3所示，机载天线接收到的信号主要分为2部分，一部分是来自地面发射的直射路径(LOS)信号，另一部分是通过反射路径反射回来的信号，反射信号由多个服从高斯分布的独立信号相叠加，故反射信号服从瑞利分布，机上接收天线接收信号整体服从莱斯分布。

图3 飞机巡航场景

复数值的信道响应：

h=a·ej2πfDLOSkTs+c·hk

(7)

式中：fDLOS为直射径的多普勒频移，a·ej2πfDLOSkTs为主径分量，a为主径幅度，是一个常实数；c·hk是反射径分量，c是常实数，hk是多个不同多普勒频率正弦波的归一化合成波幅度，是一个复变量。莱斯因子定义为：

(8)

一般来说，反射分量是非均匀分布，反射波的波束通常假设为3.5°，其时延功率谱与多普勒功率谱见图4。

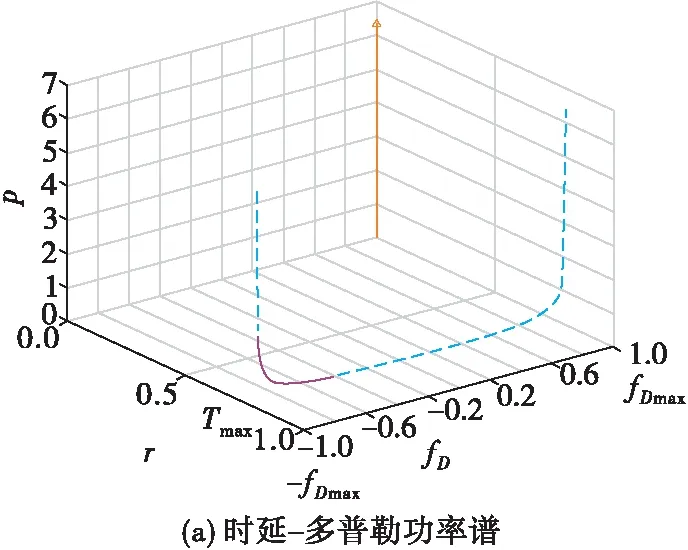
图4 两径信道时延功率谱与多普勒功率谱

此外，实测信道[1-2]表明航空信道除了零时刻和最大延时时刻有能量外，在其他时刻也存在能量分布，但整体仍呈现稀疏特性。

2.2 压缩感知原理

压缩感知(Compressed Sensing，CS)由D.L.Donoho等科学家于2004年提出[11]，被广泛应用于图像处理、计算机科学、信号处理等领域[12-14]。

考虑一维离散信号x∈RN，存在正交基Ψ={ψ1,ψ2,…,ψM}T(Ψ一般为N×N的Hermite矩阵)，使得x在该基底下可以表示为：

x=ΨHθ

(9)

式中：θ=[θ1,θ2,…,θN]T中只有K个较大值，其他值均很小，且K≪N，则信号x在Ψ域上是K稀疏的，θ为x在Ψ域下的稀疏向量。

考虑一般的线性变换，原始信号x与空间RN中一组向量集合Φ={φ1,φ2,…,φM}T的M(M≪N)个内积，得到：

y=Ax=ΦΨHθ

(10)

式中：y=[y1,y2,…,yM]T为观测量；A=ΦΨH为传感矩阵；Φ为测量矩阵。当Φ满足约束等距RIP(Restricted Isometry Property)条件时[15]，可以采用压缩感知恢复算法求解θ，利用式(9)恢复x。

由上面的分析可知，采用压缩感知的方法对信道进行估计的关键是构建满足RIP条件的测量矩阵Φ。同时，为了提高信道估计的精度，测量矩阵Φ还需要满足互不相干特性MIP(Mutual Incoherence Property)[16]。

定义1：对于测量矩阵Φ，互不相干特性要求构成测量矩阵的各列向量(‖φk‖2=1,1≤k≤N)的相干特性要尽量小，以保证估计性能，即：

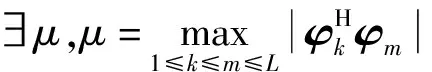
s.t.(2K-1)μ<1

(12)

式中：K为离散信号x的稀疏度，测量矩阵Φ不仅要满足RIP条件，并且μ越小，信道的估计精度越高。

目前，应用在OFDM系统的测量矩阵主要是随机矩阵和部分傅里叶矩阵，这些矩阵虽然满足RIP特性，但其MIP特性不是最优的，信道估计性能下降。因此，需要为SC-FDE系统设计专门的测量矩阵。

2.3 构造测量矩阵

在SC-FDE系统的接收端，由于无法准确获得信道长度L，因此，假设L等于导频块长度N。SC-FDE系统的帧结构使得CP与导频相同的情况下，可以将导频序列与信道冲激响应的线性卷积转换为循环卷积，接收到导频序列为：

yp=p⊗h+n

(13)

式中：p=[p1,p2,…,pN]T为发送的导频信号；h为信道响应，具有时域稀疏特性；n为复高斯白噪声序列；⊗表示循环卷积。

式(13)可以进一步写为：

yp=Ch+n

(14)

式中：C为导频信号组成的导频矩阵：

(15)

下面分析C的MIP特性，验证C是否可以直接作为测量矩阵。C的MIP特性可以表示为：

(16)

式中：cm为C的第m列，mod为取模运算。

由式(16)可知，可以通过具有最优循环相关特性的序列来构造满足MIP特性的测量矩阵。SC-FDE系统中常采用m序列，其循环相关特性表示为：

(17)

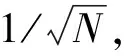
(18)

r=Φh+v

(19)

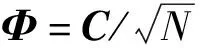
2.4 恢复算法

压缩感知中常见的恢复算法包括：正交匹配追踪(OMP)、压缩采样匹配追踪(Compressive Sampling Matching Pursuit，CoSAMP)和分段匹配追踪(Stagewise Orthogonal Matching Pursuit，StOMP)等算法[23]。这些算法的应用以知道信道稀疏度为前提，而飞行过程中航空信道的稀疏度往往是未知的，因此这些方法存在局限性。基于稀疏度自适应匹配追踪(SAMP)算法，可以自适应信道稀疏度，能准确估计出抽头位置和个数，满足实际需求。

综上，本文针对巡航状态下稀疏度K未知的航空稀疏信道估计问题，基于压缩感知框架，提出了PN-SAMP算法：利用PN序列的循环移位特性构造测量矩阵，在重构算法上选择可以自适应稀疏度K的SAMP算法来恢复信道冲激响应。

2.5 复杂度分析及比较

PN相关算法估计信道的表达式[7]：

(20)

在导频长度为N的情况下，PN相关算法共需要N3次乘法和N2-1次加法。

LS算法估计信道的表达式[6]：

(21)

采用LU分解求逆运算共需要N3次乘法和N3次加法运算，因此，LS算法共需要3N3+N2次乘法和N3+5N2-N-1次加法。

压缩感知类算法分为2步：优化测量矩阵Φ的构造和恢复算法。由于C为N×N的矩阵,因此Φ的构造需要N2次乘法，恢复算法由于涉及迭代、字典查询等运算，统计较为复杂，因此采用比较运行时间的方式来对比算法的复杂度。如图5，在MATLAB R2018b中对4种算法进行500次蒙特卡洛仿真，得到不同信道长度下算法运行时间的统计平均。

图5 算法运行时间对比

从图5可以看出，LS算法的运行时间与PN算法相近，当信道长度较长时，二者运行时间才出现明显差距，原因在于随着信道长度变大，LS算法中求逆的计算量以三次方增长。压缩感知类算法的运行时间明显长于PN算法和LS算法，而PN-SAMP算法的运行时间在信道长度大于50时，几乎是OMP算法的2倍，算法复杂度较高。

3 仿真实验

本节设置2个仿真实验：一是验证利用PN序列构造出的测量矩阵的RIP特性，二是验证本文算法相较其他信道估计算法的性能，主要指标包括信道估计的均方误差以及算法结合MMSE均衡应用在SC-FDE系统中的误码率。

3.1 确定性测量矩阵的RIP特性实验

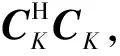
从图6可以看出，由确定矩阵抽样构建的Gram矩阵相较其他2种随机矩阵抽样构建的Gram矩阵，其最大和最小奇异值均值更接近1，因此，由PN序列构造的优化确定矩阵列与列之间的不相干特性更好，信道估计更加准确。

图6 奇异值分布

3.2 不同信道估计算法下SC-FDE系统的误码特性实验

飞机在巡航状态下，航空信道的莱斯因子一般为2～20 dB[10]，设置仿真信道KRice=4 dB，飞机飞行最大速度vmax=440 m/s，信道最大时延τmax=33 μs，设置信道长度L=31，采样周期Ts=1.06 μs，符号速率Rs=Ts=1.06 μs。帧结构参照图1，设置长度为31 bit的m序列作为导频序列，CP与导频序列内容相同，数据块长度为1 024 bit，采用QPSK数字调制方式，生成512个符号。选择滚降系数为0.33的根升余弦成型波进行1∶3的上采样，载波频率设置为300 MHz。以图4的两径模型为基础，设置2个位置随机的中间抽头量，以模拟飞行过程中的非两径航空稀疏信道情况，每个散射分量hk均由200个正弦波合成得到，最终生成服从莱斯分布的稀疏多径复信道h。

图7为第k帧数据传输时的信道抽头绝对值，从图中可以看到，信道的零延迟分量最大，最大延迟分量次之，其他反射分量较小。图8为该信道的幅频特性曲线，表明第k帧数据传输时所面临的是一个深衰落信道，最大可达-20 dB，信道特性极差，接收端不做均衡处理将导致系统无法正常通信。

图7 第k帧数据传输时的信道抽头绝对值

图8 第k帧数据传输时的信道幅频特性曲线

在接收端，同时采用PN算法、LS算法、PN-SAMD算法。图9是信噪比为20 dB的情况下，4种算法对信道实部的估计情况，虚部估计情况类似。从图中可以看出，相较PN算法和LS算法，压缩感知类算法更接近已知信道抽头分布，尤其是OMP算法在输入稀疏度K与已知信道一致时，其性能最优。但是当K输入发生错误时，采用OMP恢复算法的信道估计性能变差，如图10(b)所示，漏掉了一部分反射分量的能量，导致估计不准确。图11为以上4种算法的MSE曲线，同样可以观察到压缩感知类算法的估计准确度要优于PN算法和LS算法。当信道稀疏度的先验知识未知的情况下，OMP算法会出现比较大的估计误差。

图9 SNR=20 dB时，4种算法的抽头实部估计情况

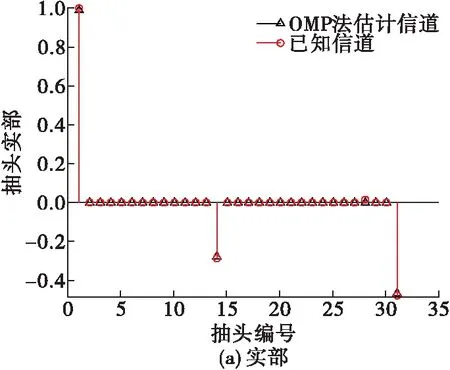
图10 SNR=20 dB,输入K=3时,OMP算法估计信道情况

图11 估计信道的MSE曲线

图12为4种算法估计信道得到的SC-FDE系统误码率曲线，从图中可以看出，PN算法的最终误码率曲线保持在0.1以上，几乎不随信噪比变化，原因在于PN算法估计误差的主要来源是残留矩阵，信噪比提升对算法误差影响不大。LS算法的误码性能优于PN算法，误码特性会随着信噪比的提升而提升。PN-SAMP算法的误码性能优于LS算法，劣于OMP算法，但是当稀疏度输入错误时，OMP算法的误码特性明显变坏(OMP-Wrong)。虽然PN-SAMP算法的误码性能不是最优的，但是由于其可以自适应信道稀疏度，不受稀疏度的先验信息影响，因此，采用PN-SAMP算法作为压缩感知的恢复算法更加稳健，更能满足我们的实际工程需求。

图12 SC-FDE系统误码率曲线

4 结语

针对航空信道稀疏特性，基于压缩感知的框架，本文提出了一种PN-SAMP信道估计算法，该算法利用PN序列构造确定测量矩阵，以SAMP作为恢复算法。仿真结果表明，确定测量矩阵的RIP特性优于随机测量矩阵，在SC-FDE系统的误码率特性中，压缩感知类算法比传统的PN相关算法和LS算法对信道估计更准确，误码率更低，在信噪比为20 dB的条件下，误码率小于10-4。在恢复算法的比较中，SAMP算法比OMP算法更稳健，更能满足稀疏度未知的实际情况下对航空稀疏信道进行估计的需求。