拱肋与系梁连接部位受力分析及设计优化
2020-12-17储胡照中铁上海设计院集团合肥有限公司安徽合肥230011
储胡照 (中铁上海设计院集团合肥有限公司,安徽 合肥 230011)
1 引言
下承式系杆拱桥是无推力的拱式组合体系结构,由拱肋、系杆、吊杆相互联结而成。由于其具有行车道建筑高度低,对基础变位适应性强,景观效果好等优点,正越来越多地在地质条件差、桥下净空受限时被采用。下承式系杆拱桥的拱脚节点是全桥结构传力的关键部位,不仅承担着来自拱肋和系梁的内力,还承受巨大的支座反力,以及系杆锚固的局部压力。由于拱脚节点处的结构构造及受力很复杂,其受载后的应力分布用杆系理论难以给出精确的分析结果,因此采用有限元法对拱脚节点进行局部受力分析十分有必要,得到拱脚节点在三向受力下的空间应力分布规律和大小,从而指导设计对节点构造进行优化,使拱脚节点结构的设计更加合理可靠[1-2]。其中,拱脚构造中拱肋与系梁连接部分可以有多种不同形式,不同的连接方式会对结构的局部受力产生不同的影响,有时候会导致应力集中的产生,所以在进行拱脚节点构造设计时,确定合理的拱肋与系梁连接形式有利于保证结构的安全可靠。
基于此,本文以拟建的某单跨85m下承式钢筋混凝土系杆拱桥为工程背景,采用通用有限元分析软件ABAQUS对此桥拱脚节点进行局部受力分析,研究了不同的拱肋与系梁连接形式,对于拱脚节点局部受力特征的影响。
2 工程背景
某单跨下承式钢筋混凝土系杆拱桥,桥跨布置为3m×25m小箱梁+85m系杆拱+4m×25m小箱梁,全长266m,桥梁全宽41m。为刚性系杆刚性拱,计算跨径L=83m,拱轴线为二次抛物线,矢跨比为1/4,矢高20.75m。拱肋采用工字型截面,拱肋高1.4m、宽1.2m。全桥设置5道工字型混凝土风撑。
系杆采用等截面箱梁,系杆高2.2m,宽1.8m,每片拱片设间距为4m的吊杆18根,风撑设置5道,采用工字型截面,高1.8m、宽1.2m。端横梁高度为2.34m~2.62m;中横梁高度为0.8m~1.83m,梁顶设有0.29m后浇混凝土,桥面双向1.5%横坡,通过横梁高度的变化,调整桥型总体布置和横断面,见图1和图2所示,拱脚局部构造见图3。
3 计算方法及局部有限元模型
3.1 计算方法
结构整体分析通常是以杆系理论为依据,计算出结构在恒载、活载、温度等各种作用下,不同截面处的内力、应力和位移等[3],但由于结构的某些关键部位构造复杂,整体模型的结果不能够准确反映复杂节点部位的分布情况[4-6],所以对于所分析的局部构造,需要建立实体单元的精细模拟,然后进行有限元分析。
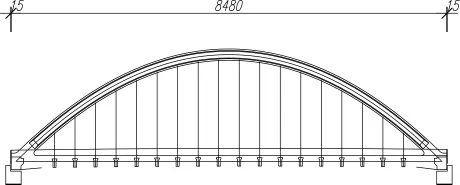
图1 桥型总体布置图(单位:cm)
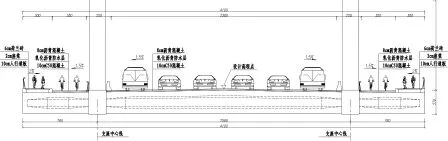
图2 梁标准断面示意图(单位:cm)
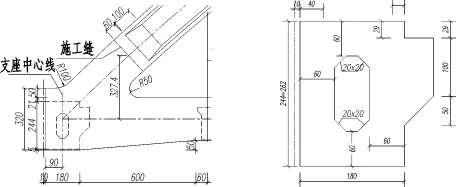
图3 拱脚局部构造(单位:cm)
本文在进行拱脚模型分析时采用了“子模型法”。第一步,采用Midas/civil软件建立全桥的有限元模型,考虑恒载、活载的影响,并且根据相关规范对其进行相应的荷载组合,进行计算分析得到全桥的整体受力情况,全桥的有限元模型如图4所示。第二步,考虑圣维南原理的情况下,截取恰当的拱脚节点尺寸,采用实体单元建立拱脚局部有限元模型,将Midas/civil中提取的所需分析工况拱脚各截面的内力结果,通过刚性面法施加在模型的各断面处,然后再施加边界条件进行分析,即可得到精确的拱脚局部模型的应力状态。
3.2 有限元模型
局部分析时,需要施加内力边界条件和位移边界条件,为了保证节点局部分析结果的精确度,内力边界条件施加位置应离节点较远,但截取长度过长会导致有限元模型单元数太多,耗时低效,故不能太长[3],本文考虑圣维南原理截取范围为:拱肋取4m,系梁沿顺桥向取6m,端横梁取7m(沿拱肋轴线对称各取3.5m)。
采用大型有限元分析软件ABAQUS建立拱脚局部有限元精细化模型,分别建立了三种不同的拱肋与系梁连接形式的局部有限元模型,倒角形式分别为圆角、直角和钝角。在此给出圆角倒角形式的拱脚局部有限元模型,见图5。

图4 全桥有限元模型

图5 拱脚有限元模型(圆角)
3.3 荷载及边界条件施加
在进行拱脚局部应力分析时,应防止结构发生刚体位移,保证整个结构为静定结构。局部模型所施加的荷载是从Midas/civil全桥整体模型的相应位置处提取,包括拱肋、系梁和端横梁位置的内力。下表给出了Midas/civil承载能力极限状态荷载组合下结构的内力,所提取结果为在全桥模型的单元坐标系输出的,根据静力等效的原则,在进行局部模型荷载的施加时,需要将全桥模型的内力结果,转化为局部模型的坐标系所对应的内力。
4 结果分析及优化设计
4.1 圆角
将拱肋与系梁连接部位设置成倒圆角,划分网格,在拱肋、系梁和端横梁截面施加内力,其Mises应力云图、Magnitude应变云图分别见图6、图7。由分析结果可知,拱肋倒圆角时,第一主拉应力在系梁表面交界处为1.25MPa,在拱肋底部下边缘1.79MPa;第二主应力在系梁表面交界处为-0.14MPa,在拱肋底部下边缘为-0.12MPa;第三主压应力在系梁表面交界处为-1.34MPa,在拱肋底部下边缘-17.5MPa。拱肋倒圆角时,结构截面最大变形为5.66mm。

图6 拱脚Mises应力云图(圆角)

图7 拱脚Magnitude应变云图(圆角)
4.2 直角
将拱肋与系梁连接部位设置成直角,划分网格,在拱肋、系梁和端横梁截面施加内力,其Mises应力云图、Magnitude应变云图分别见图8、图9。由分析结果可知,拱肋倒圆角时,第一主拉应力在系梁表面交界处为1.47MPa,在拱肋底部下边缘3.05MPa;第二主应力在系梁表面交界处为1.02MPa,在拱肋底部下边缘为-2.31 MPa;第三主压应力在系梁表面交界处为0.81MPa,在拱肋底部下边缘-16.53MPa。拱肋倒圆角时,结构截面最大变形为3.92mm。
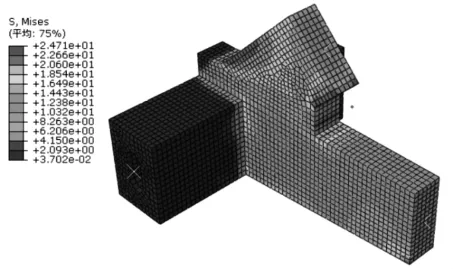
图8 拱脚Mises应力云图(直角)

图9 拱脚Magnitude应变云图(直角)

承载能力极限状态拱脚内力结果
4.3 钝角
将拱肋与系梁连接部位设置成钝角,划分网格,在拱肋、系梁和端横梁截面施加内力,其Mises应力云图、Magnitude应变云图分别见图10、图11。由分析结果可知,拱肋倒圆角时,第一主拉应力在系梁表面交界处为1.39MPa,在拱肋底部下边缘2.76MPa;第二主应力在系梁表面交界处为0.89MPa,在拱肋底部下边缘为-0.17 MPa;第三主压应力在系梁表面交界处为0.45MPa,在拱肋底部下边缘-20.25MPa。拱肋倒圆角时,结构截面最大变形为5.04mm。

图10 拱脚Mises应力云图(钝角)
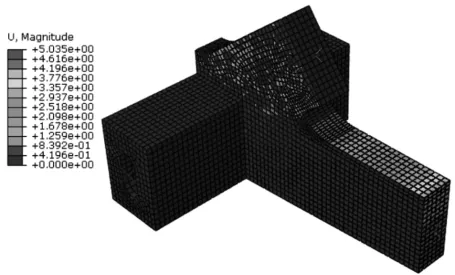
图11 拱脚Magnitude应变云图(钝角)
5 结论
对比三种不同的拱肋与系梁处连接的倒角形式,可以得出以下结论:
①当采用直接倒圆角的形式时,拱脚结构的第一主拉应力远小于混凝土的抗拉强度设计值,能够有很大的安全储备,同样对应的第二主应力、第三主应力均小于材料的容许应力值;
②当采用直角连接的形式时,拱脚结构的第一主拉应力超过了混凝土的抗拉强度设计值,已经发生了开裂,而对应的第二主应力、第三主应力均小于材料的容许应力值;
③当采用钝角连接的形式时,拱脚结构的第一主拉应力超过了混凝土的抗拉强度设计值,已经发生了开裂,而对应的第二主应力、第三主应力均小于材料的容许应力值;
④而对于三种连接形式下,拱脚结构的局部最大变形较为接近,可见不同的拱肋与系梁处连接形式对于结构的局部变形影响较小。
综上所述,对于下承式钢筋混凝土系杆拱桥拱脚系梁处连接形式采用直接倒圆角的形式是较为合理的。
