基于多种材料模型的混凝土/基岩胶结面现场抗剪试验的数值模拟研究
2020-12-17王义鹏赖国伟
王义鹏,赖国伟,程 亮,余 巍,朱 东
(1.中南电力设计院有限公司,武汉 430071;2.武汉大学 水资源与水电工程国家重点实验室,武汉 430072)
0 引 言
重力坝作为人类最早使用的一种水坝坝型,其抗滑稳定一直是学者比较关心的问题,同时,重力坝与基岩的胶结面作为一种特殊的结构面,对重力坝的抗滑稳定起着控制作用。对于沿坝基面的抗滑稳定分析,《混凝土重力坝设计规范(SL319-2018)》[1]推荐了两种计算公式:摩擦公式和抗剪强度公式。这两种公式中的抗剪摩擦系数f和抗剪断摩擦系数f′、抗剪断凝聚力c′的取值对抗滑稳定有很大的影响,如果选取的数值偏大,则坝基的稳定性得不到保证;反之,则偏于保守,造成不必要的浪费。
《混凝土重力坝设计规范(SL319-2018)》[1]规定坝体混凝土/基岩胶结面的f、f′、c′的取值在可行性研究阶段及其后的各设计阶段应经现场抗剪试验确定。李仕胜(1997)[2]认为岩性和试验正应力大小是影响胶结面抗剪强度的主要因素,林伟平等[3]认为胶结面的粗糙度对抗剪强度有显著影响,Haberfield和Seidel[4]通过总结室内试验的结果提出了基于分形几何概念的模拟剪切行为的理论模型。但物理模型试验不能反映剪切过程中的应力状态,不能让人很直观地了解整个试验的剪切破坏过程,而且现场抗剪试验是在假设剪切面的应力分布为均匀分布的条件下得出的,与实际的破坏过程不相符,其结果必然存在误差。如今,随着有限元计算方法的快速发展以及其方法的通用性和有效性,有限元数值计算在工程技术界得到了广泛的应用,王宏硕等[5]通过平面弹性有限元计算,指出混凝土试块与基岩胶结面上的应力分布是极不均匀的;邓建文[6]在王宏硕等[5]的成果上采用三维弹性有限元进一步验证了剪切面上的应力不均匀性及弹模比对胶结面应力分布的影响。前人的研究大多只使用单一的材料模型,缺乏不同材料模型之间的对比,有失客观性。本文采用多种不同的材料模型模拟混凝土/基岩胶结面,通过数值计算分析现场抗剪试验中胶结面的剪切破坏过程及应力、变形状态,进而对现场抗剪试验得出的参数进行评价。
1 材料模型简介
1.1 Mohr-Coulomb 材料模型
Mohr-Coulomb强度准则在岩土工程中的应用非常广泛,大量的岩土工程设计计算都采用了Mohr-Coulomb强度准则[7]。
(1)屈服函数。Mohr-Coulomb材料模型的屈服轨迹如图1和图2所示,表达式为:
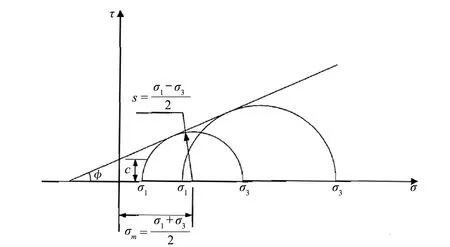
图1 Mohr-Coulomb材料模型
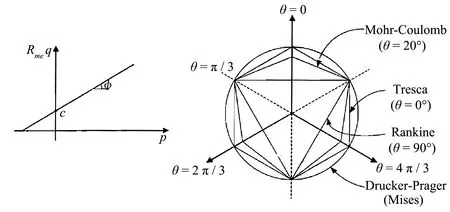
图2 Mohr-Coulomb材料模型在子午面和π平面上的屈服面
(1)
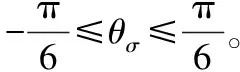
(2)流动势函数。G为流动势函数,表达式如下所示:
(2)
式中:ψ是剪胀角;c|0是初始黏聚力,即没有塑性应变时的黏聚力;∈为子午面上的偏心率,它控制了G在子午面上的形状与函数渐近线之间的相似度。Rmw则控制了其在 π 平面上的形状。
1.2 节理材料模型
ABAQUS/Standard提供了一种节理材料模型[7],该模型可以模拟其裂隙成组出现且有规律的节理岩体。
节理材料模型主要应用于材料受压的情形,但也规定了节理的张开能力,当垂直节理面即将变为拉伸时,此时,假定材料裂隙的法向没有弹性刚度,只有应变,由于节理面的张开,导致了节理面的各向异性弹性。
节理材料模型的塑性行为被单独的分为两部分,一部分是节理体系的塑性行为,另一部分是岩块材料的塑性行为,两者的屈服准则各不相同。
1.2.1 节理体系的塑性行为
节理体系a的滑动破坏面定义如下:
fa=τa-patanβa-da=0
(3)
式中:βa为节理体系的内摩擦角;da为节理体系的黏聚力,如图3所示;τa为节理面上的剪应力;pa是作用在节理面上的法向压应力。当fa<0时,节理体系不发生滑动。当fa=0时,节理体系滑动。此时,塑性应变为:
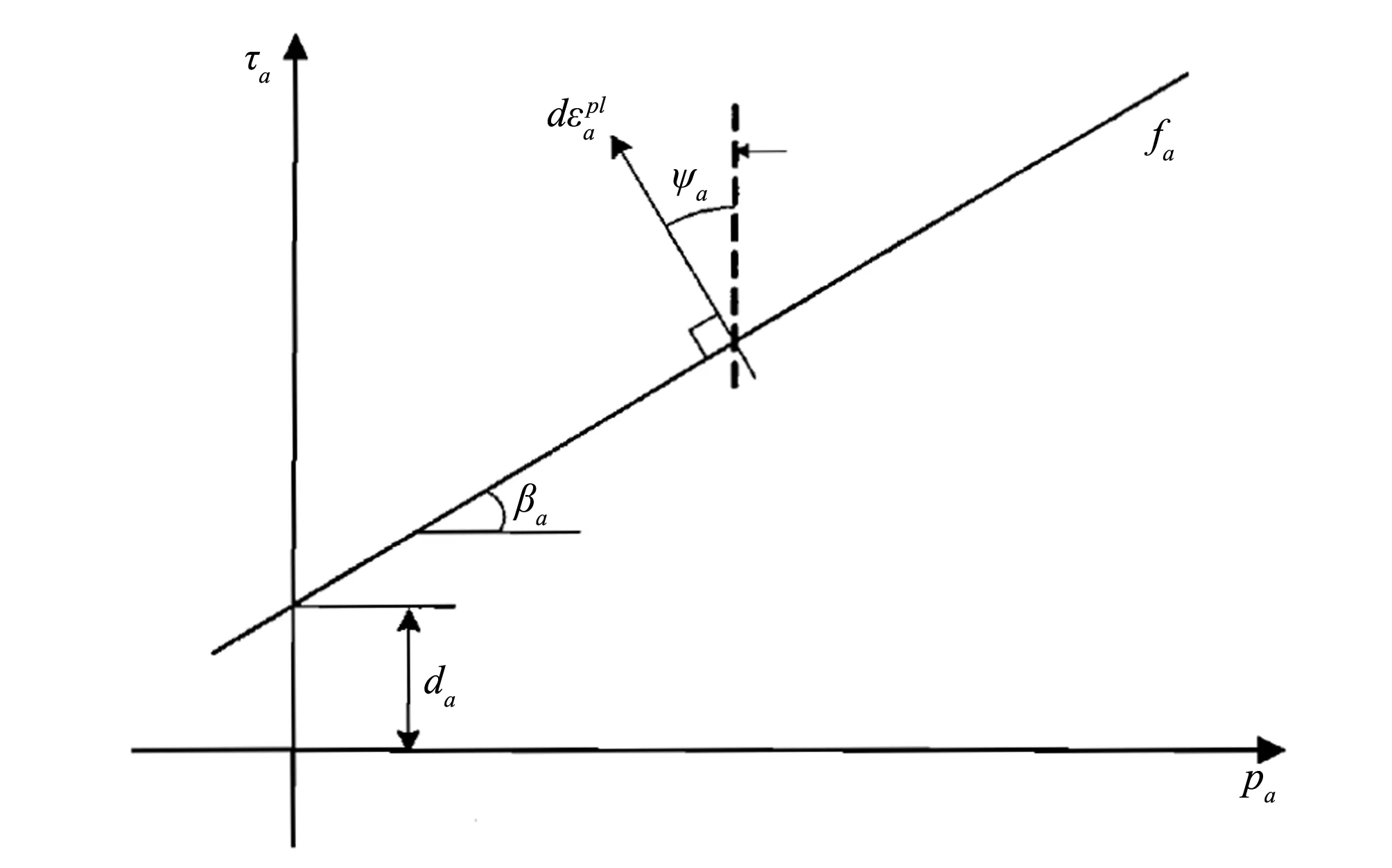
图3 节理材料模型
(4)
(5)
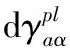
节理材料模型对同一个岩体材料提供3组独立的节理面,即在同一个点可以存在3组独立的滑动节理面,而且每个节理体系的滑动不会改变其他体系的破坏准则和膨胀角。
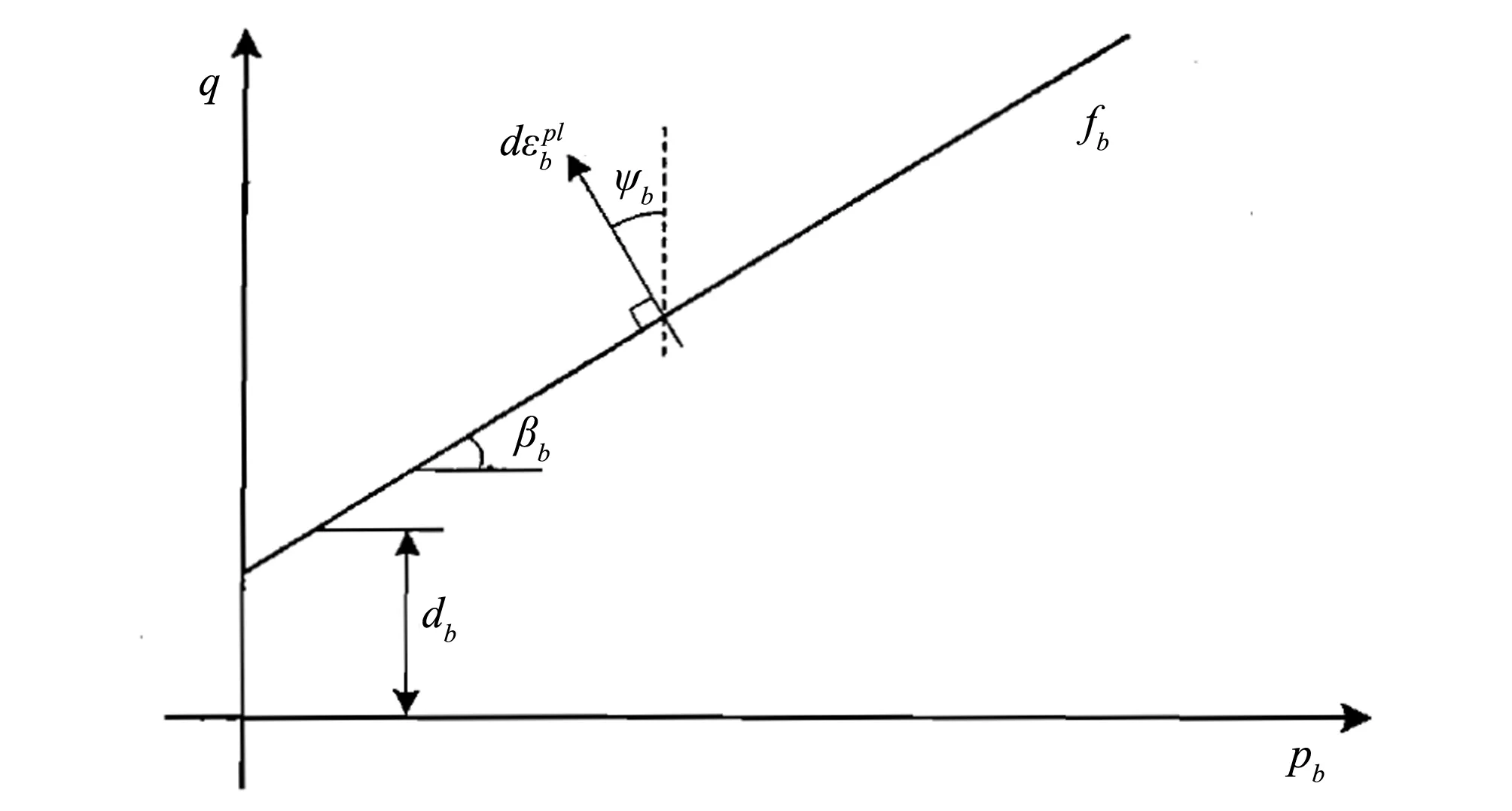
图4 岩块材料模型
1.2.2 岩块材料的塑性行为
岩块材料的破坏服从线性的Drucker-Prager破坏准则,即:
q-ptanβb-db=0
(6)
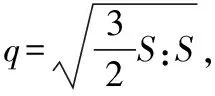
当材料达到屈服时,岩块材料的塑性流动定义为:
(7)
式中:gb=q-ptanψb是流动势函数;ψb为散体材料的膨胀角,该岩块破坏模式是扩展Drucker-Prager模型的简化形式。
岩块材料和节理体系的塑性流动都相互独立,其塑性流动都不会相互影响。
1.3 基于ABAQUS的混凝土损伤塑性模型
ABAQUS软件提供一种连续的、基于塑性的混凝土损伤塑性模型[7],该模型假定混凝土材料主要因拉神开裂和压缩破碎而破坏。
ABAQUS混凝土损伤塑性模型假定混凝土的单轴拉伸和压缩性状由损伤塑性描述,如图5和图6,并自动将用户自定义的应力-“非弹性”应变数据转换成σ-εpl关系曲线来描述混凝土的应力-应变关系。混凝土在应力-应变关系曲线的软化段上卸载时,从图中可以看出卸载的弹性刚度小于初始弹性刚度,这说明材料发生了损伤,用两个损伤变量dt和dc表示单轴拉伸和压缩下的应力-应变关系为:
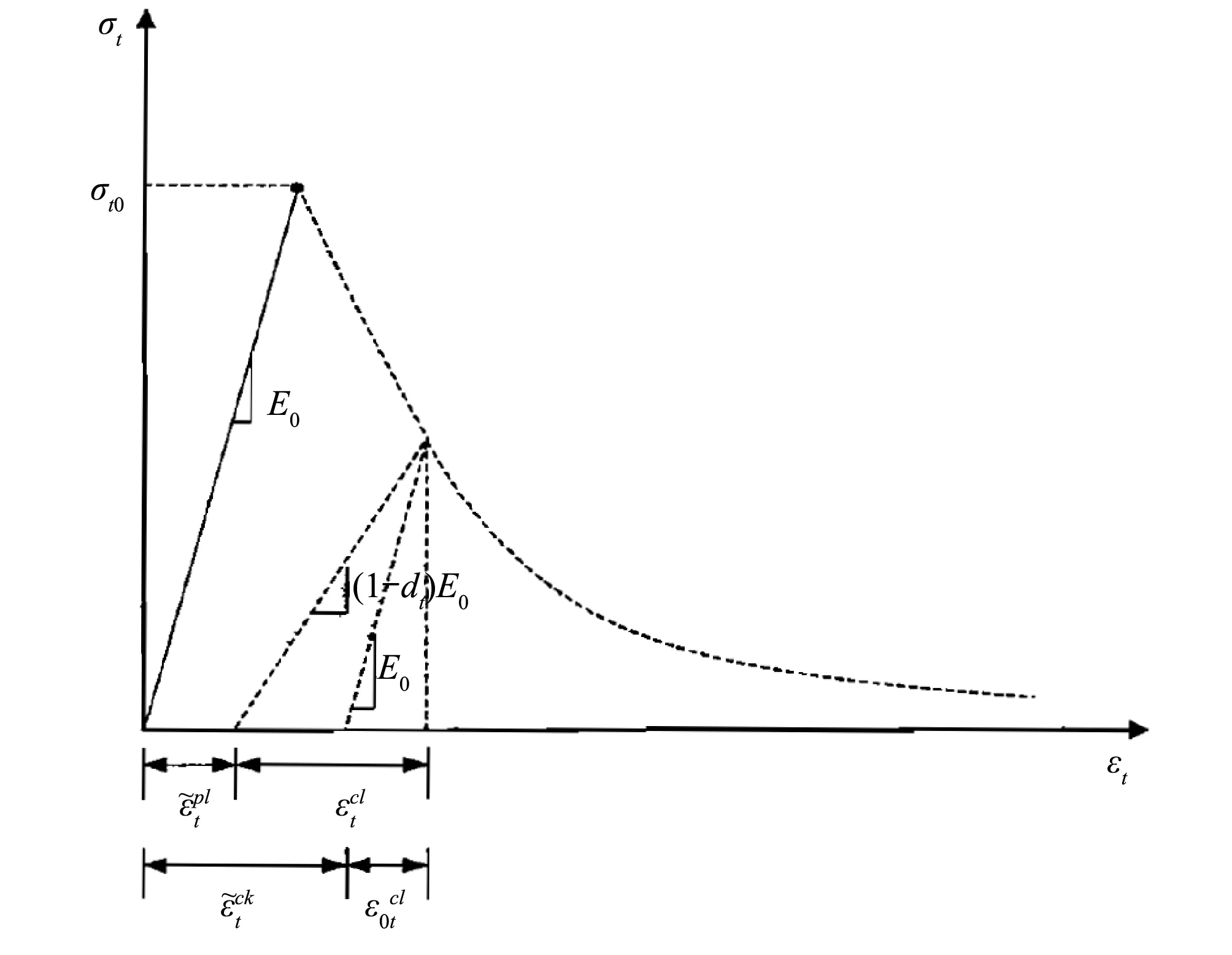
图6 混凝土单轴拉伸的损伤描述
(8)
(9)
(10)
(11)
(1)屈服函数。ABAQUS混凝土损伤塑性模型采用修正Lubliner-Fenves损伤模型的屈服面,如图7,可以考虑拉伸和压缩情况下不同的强度演化,并用有效应力来表达:
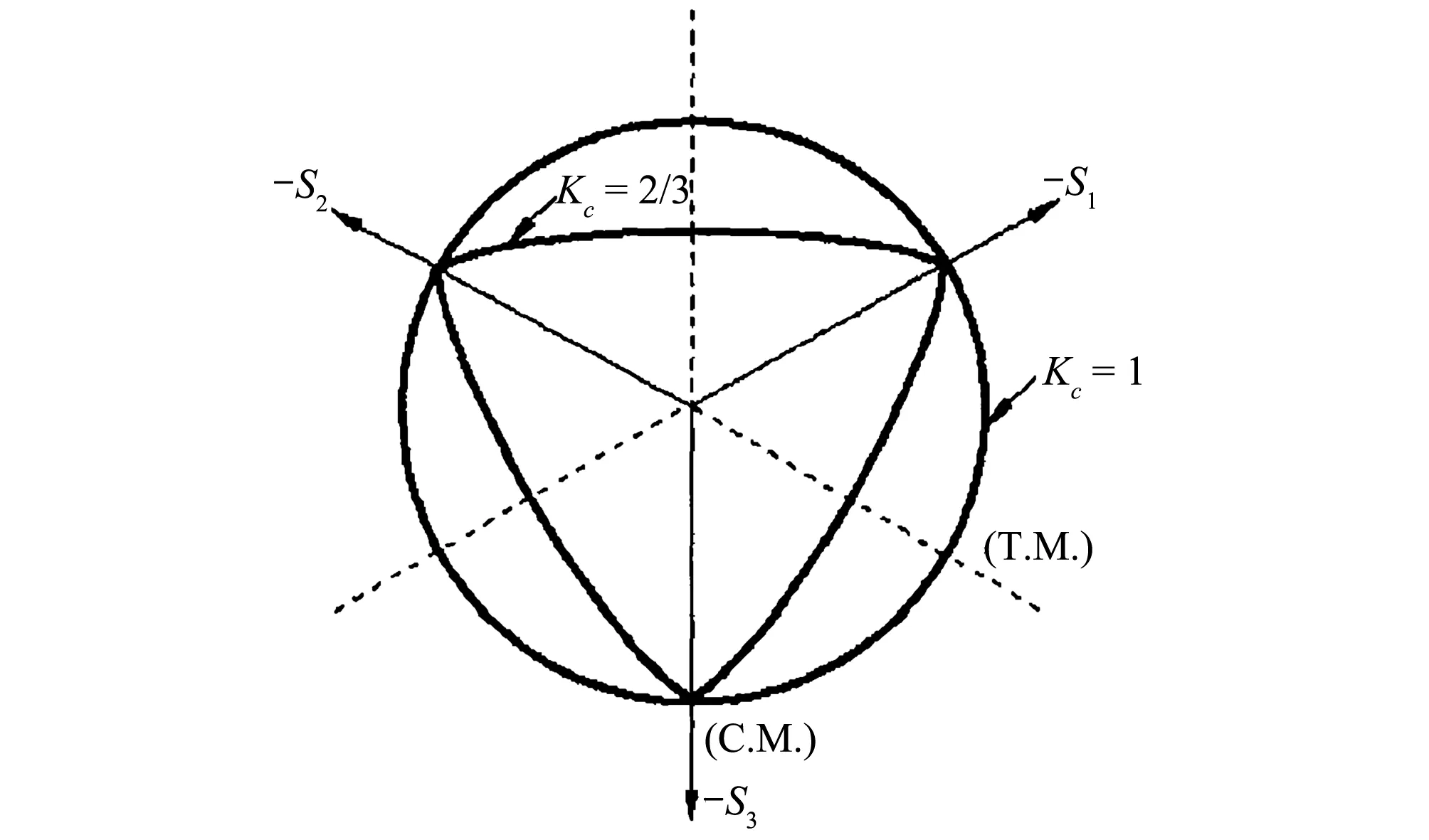
图7 修正Lubliner-Fenves损伤模型在π平面上的屈服面
(12)
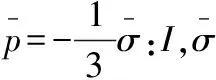
(2)流动势函数。混凝土损伤塑性模型的流动势函数采用非相关联势塑性流动。模型中所采用的流动势G为Drucker-Prager抛物线函数,即:
(13)
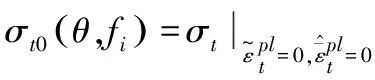
2 混凝土/基岩胶结面现场抗剪试验的数值模拟方法
2.1 有限元模型
根据《水利水电工程岩石试验规程(SL264-2001)》[8]中对混凝土/岩体胶结面直剪试验的描述,建立该试验的二维有限元模型(图8):有限元模型中胶结面沿剪切方向的长度为50 cm,厚度设为1 cm,不考虑其起伏程度;混凝土试件推力面的中心线与剪切面成15°且过剪切面的中点,试件高40 cm;基岩上下游的长度和深度均为两倍胶结面剪切方向长度,即100 cm。
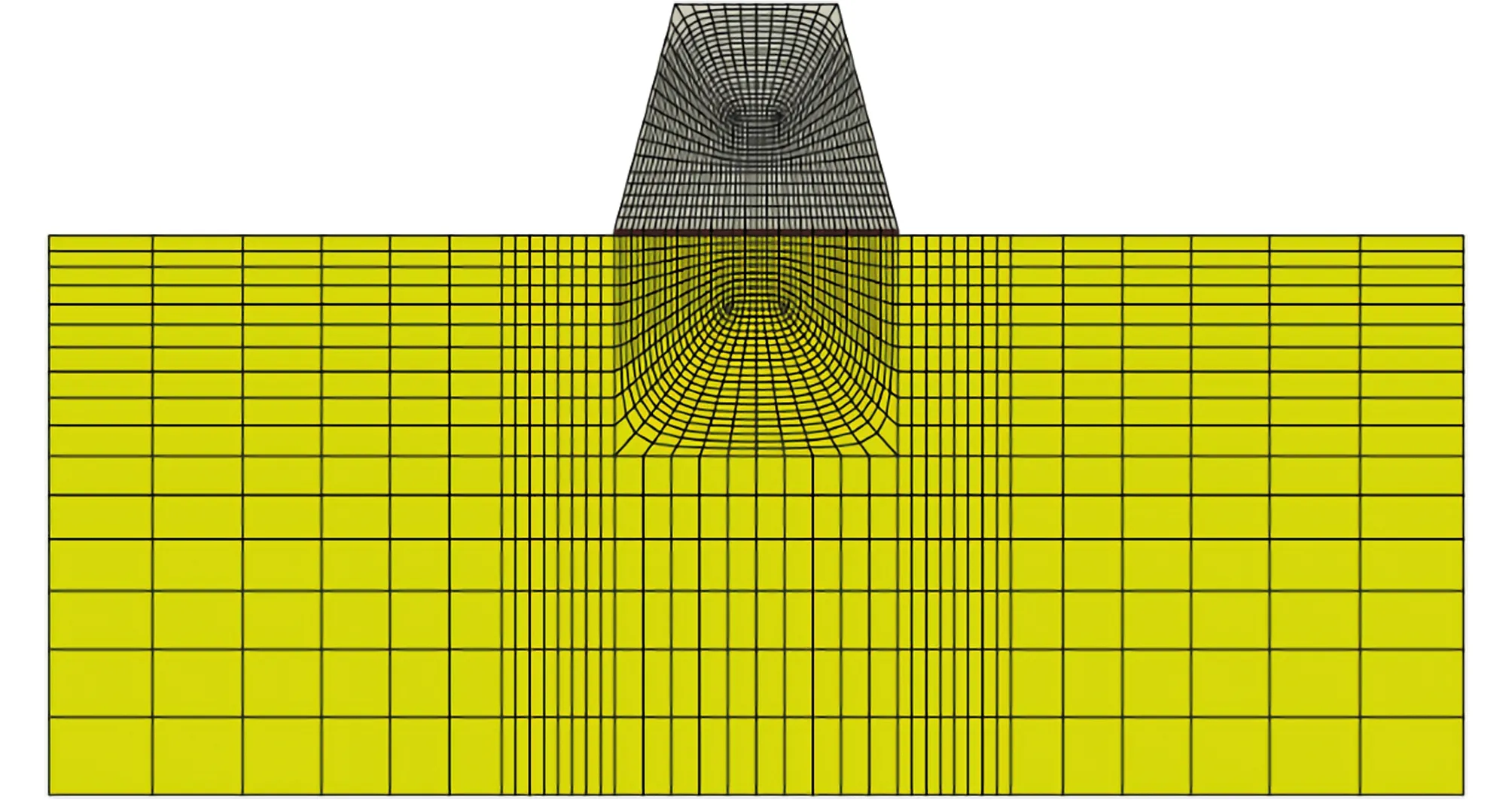
图8 二维有限元网格模型
二维有限元模型选用四边形平面应变单元(CPE4R),有单元2 208个、节点2 279个。
根据《岩基抗剪强度参数》[9]中对503组混凝土/基岩胶结面抗剪试验的统计分析,以及《混凝土重力坝设计规范(SL319-2018)》[1]中对混凝土/基岩胶结面抗剪强度参数的建议值,取混凝土试件的标号为C20(老编号200号),基岩的材料参数参考E2类岩体,具体取值见表1。其中《混凝土结构设计规范(GB50010-2010)》[10]对于C20等级的混凝土只提供了轴心抗拉强度和轴心抗压强度,因此表1中的抗剪强度参数需要通过以下公式换算而得:
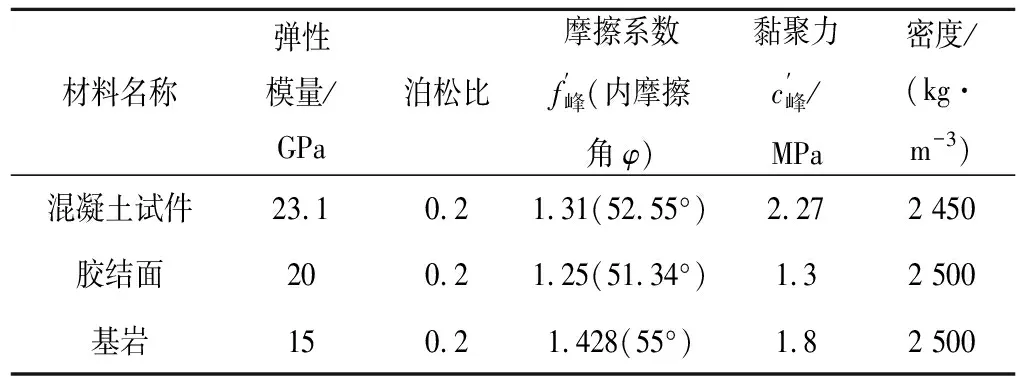
表1 各部分材料参数取值
(14)
(15)
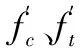
2.2 荷载施加方法
《水利水电工程岩石试验规程(SL264-2001)》[8]中对混凝土/岩体胶结面直剪试验的试验加载规定:每个试件的法向荷载分为3~5级施加;剪切荷载按照预估的最大值分8~10级施加,采用斜推法时,应同步降低因施加剪切载荷而产生的法向分量的增量,保持剪切面上的法向正应力不变。由于本文是为了研究剪切过程中胶结面的应力-应变状态,而在剪切后期胶结面的破坏十分迅速,因此需要细分剪切荷载。本文的具体荷载步骤如下:对混凝土试件顶面施加法向荷载保证剪切面上的平均法向正应力分为4个等级,分别为1.0、2.0、3.0、4.0 MPa;对于每一级法向荷载,其对应的剪切荷载分17级施加,剪切前期推力增量较大,随剪切的进行,增量减小,在增加推力的同时减小混凝土试件顶面的法向荷载,从而保持剪切面上的平均正应力为定值。
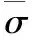
(16)
(17)
公式可简化为
(18)
(19)
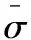
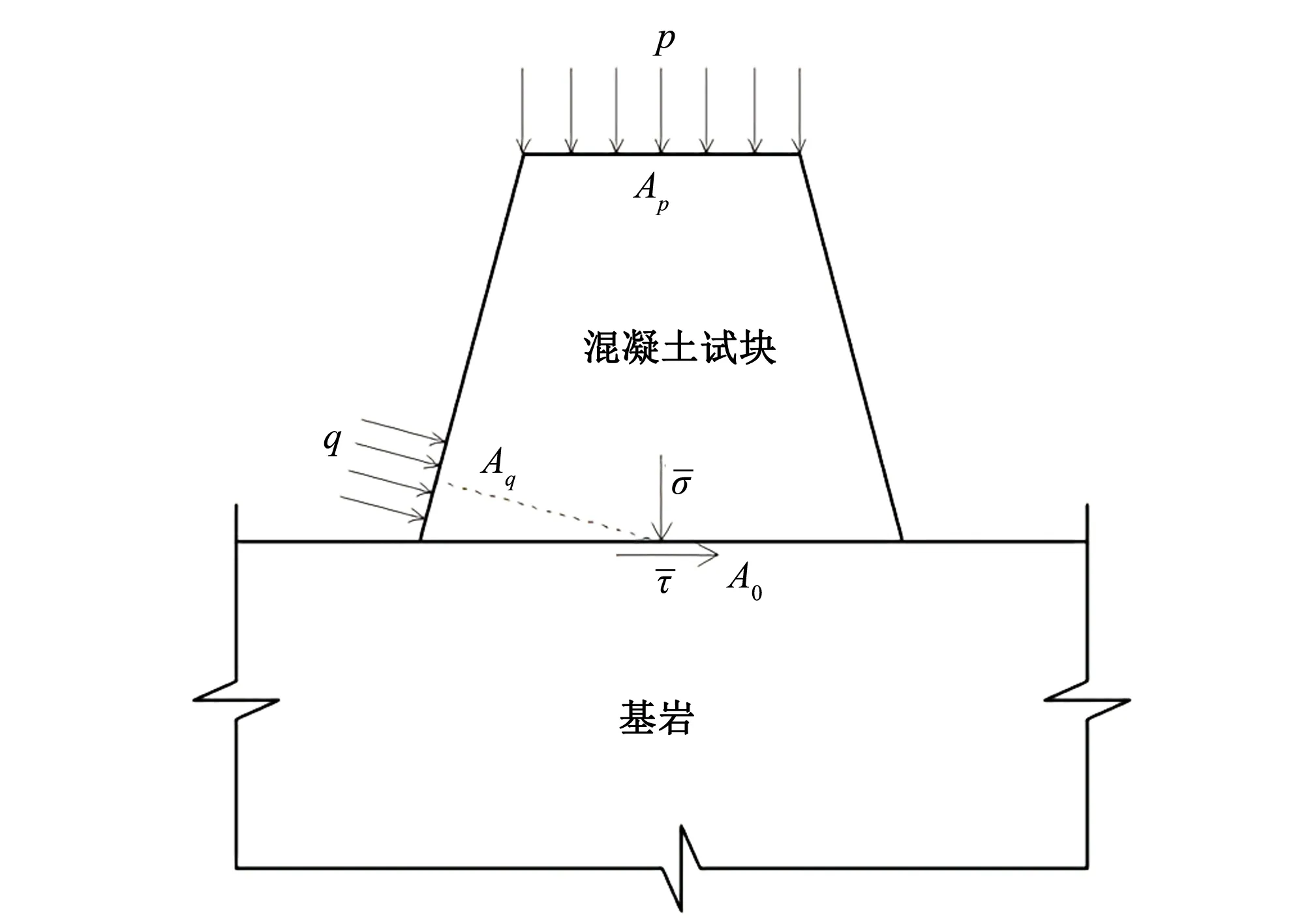
图9 系统受力示意图
2.3 本文名词解释及相关说明
为了方便后文对计算结果的分析,本文特作以下规定:
(1)平均正应力、平均剪应力:是指在假设试验系统为刚体且胶结面上的应力均匀分布的情况下,由混凝土试件顶面的法向荷载和推力面的剪切荷载通过试件几何尺寸关系换算出的胶结面上的法向正应力和切向剪应力,其大小与数值计算结果无关,在概念上等同于外荷载。
(2)法向正应力、切向剪应力:是指通过数值计算得出的胶结面上每个点的真实应力,其大小与数值计算结果相关。
(5)计算结果分析中的符号规定:法向正应力以压为负、拉为正;切向剪应力以剪切方向为正;法向位移以张开为正、压缩为负;切向位移以剪切方向为正。
(6)胶结面各节点及测点的位置说明(图10)。

图10 胶结面各节点及测点位置说明
根据《水利水电工程岩石试验规程(SL264-2001)》[8]中对现场抗剪试验装置的说明,选取图10中x=-20、x=0和x=20处的3对节点分别作为上游测点、中部测点和下游测点(每处有上下两个节点,共同组成一个测点)。
(7)后文中的切向位移和法向位移均为测点位置处上下两节点的相对位移。
3 基于多种材料模型的胶结面应力变形及破坏分析
3.1 胶结面破坏判别依据
对于数值模拟破坏的判别依据有很多,其中使用非常广泛的稳定判别依据主要有以下几种[11]:收敛性判据;屈服区贯通法;位移突变法;能量法。
现场抗剪试验的加载过程类似于拱坝的超载试验,都是在逐步增加外荷载的过程中寻找模型的破坏时刻,因此本文胶结面破坏的判别依据参考拱坝破坏的判别依据:以屈服区贯通法作为胶结面破坏的主要判别依据,胶结面测点的位移突变作为参考依据,其中将等效塑性应变大于10-5作为屈服标准。
3.2 计算结果分析
混凝土试件和基岩采用线弹性模型,胶结面分别采用节理材料模型(下文简称JOINT)、Mohr-Coulomb材料模型(下文简称M-C)、理想弹塑性的损伤塑性模型(下文简称CDP-S)和考虑软化的损伤塑性模型(下文简称CDP)进行破坏分析。
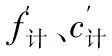
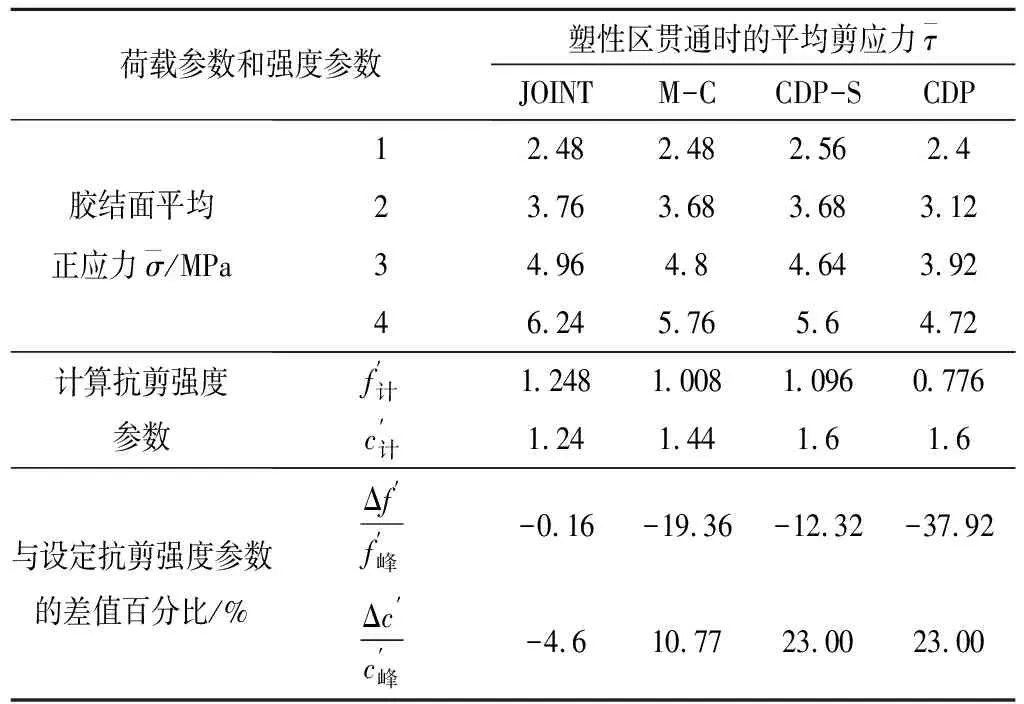
表2 计算抗剪强度参数
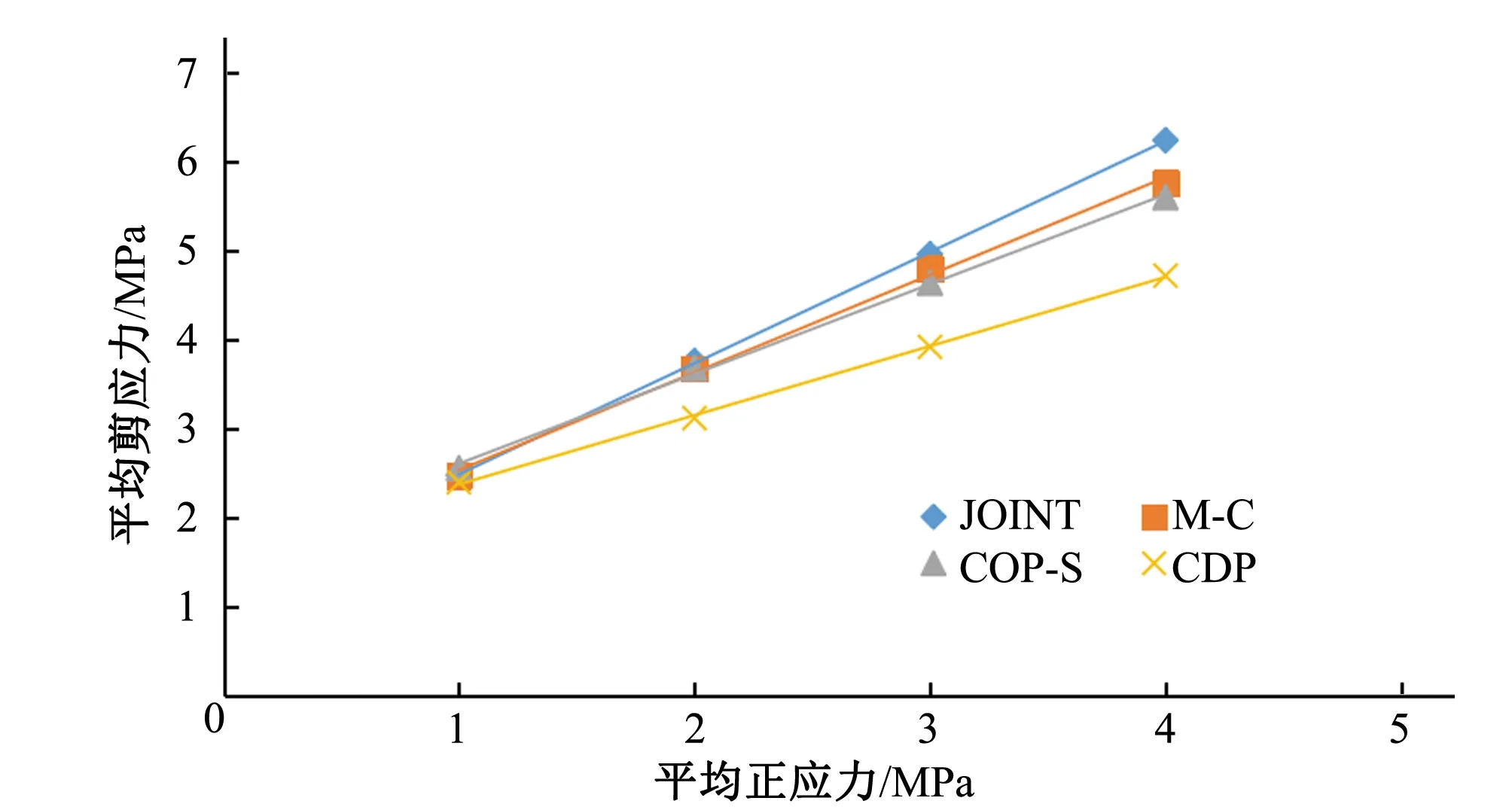
图11 平均正应力与平均剪应力散点图
3.2.2 胶结面应力分布
图12至图19所示的胶结面应力分布曲线均在平均正应力为1 MPa时平均剪应力分别为4、13、15 MPa三个荷载步下获得的。
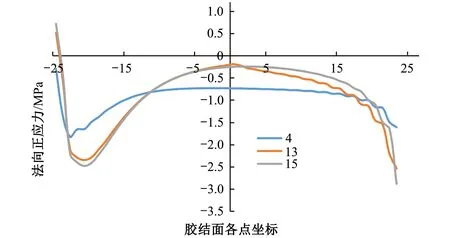
图12 JOINT不同平均剪应力下胶结面的法向正应力分布
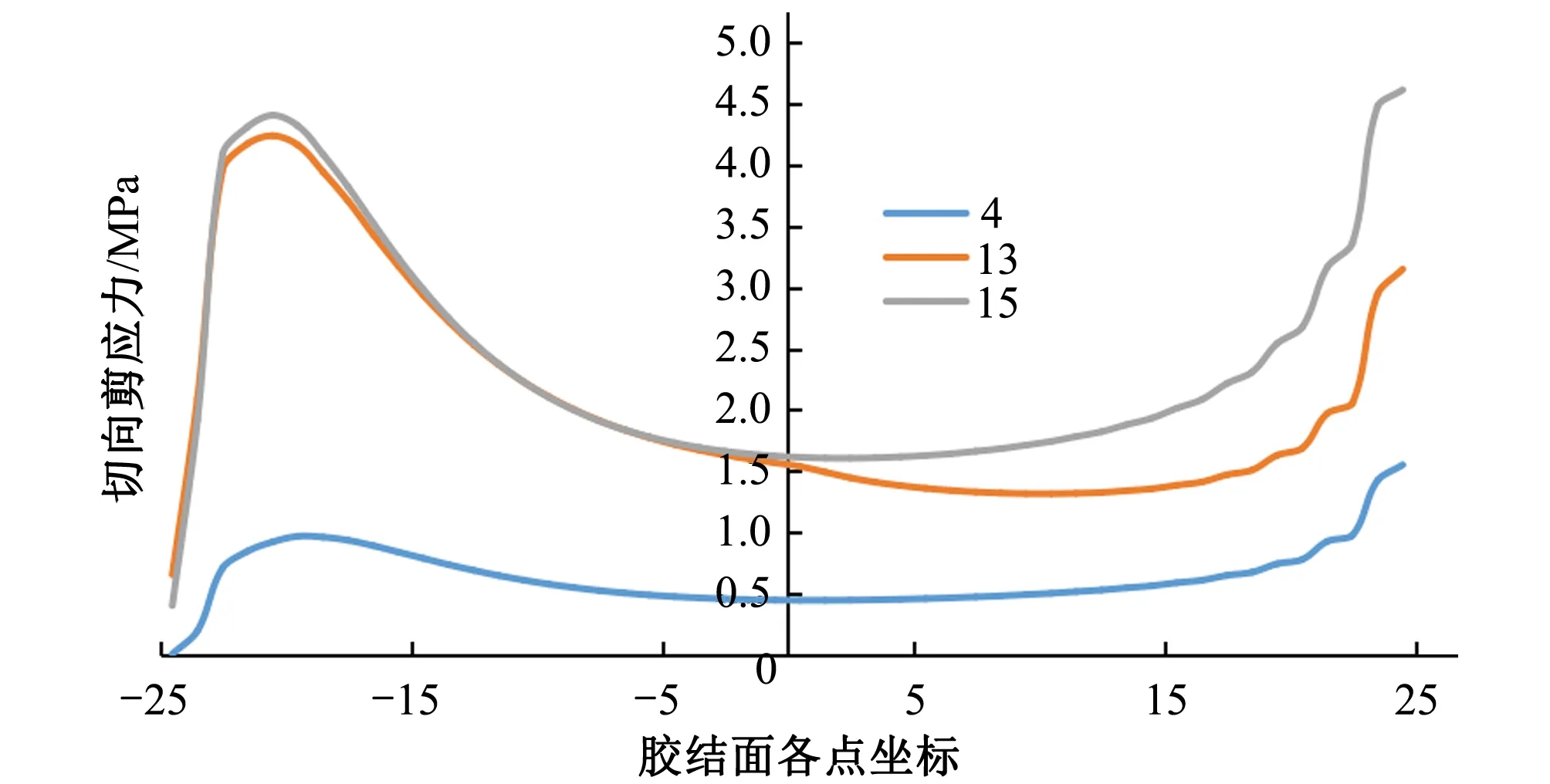
图13 JOINT不同平均剪应力下胶结面的切向剪应力分布
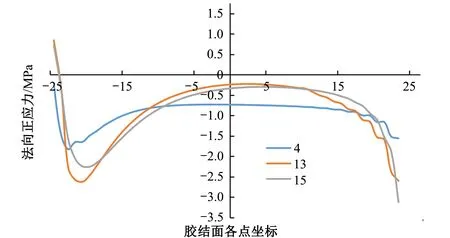
图14 M-C不同平均剪应力下胶结面的法向正应力分布
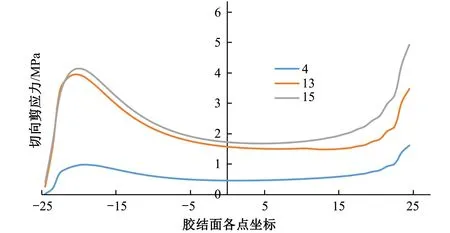
图15 M-C不同平均剪应力下胶结面的切向剪应力分布
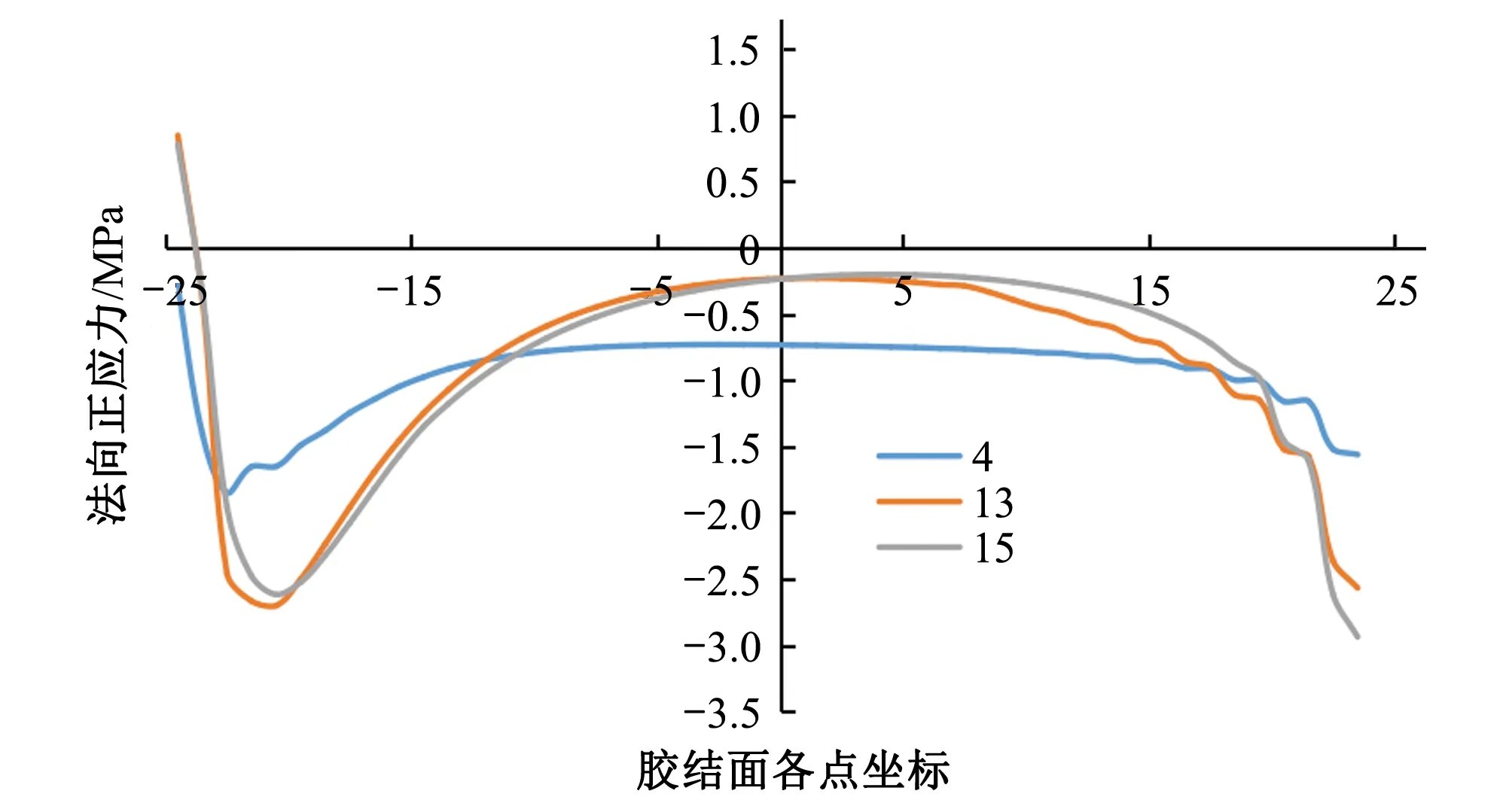
图16 CDP-S不同平均剪应力下胶结面的法向正应力分布
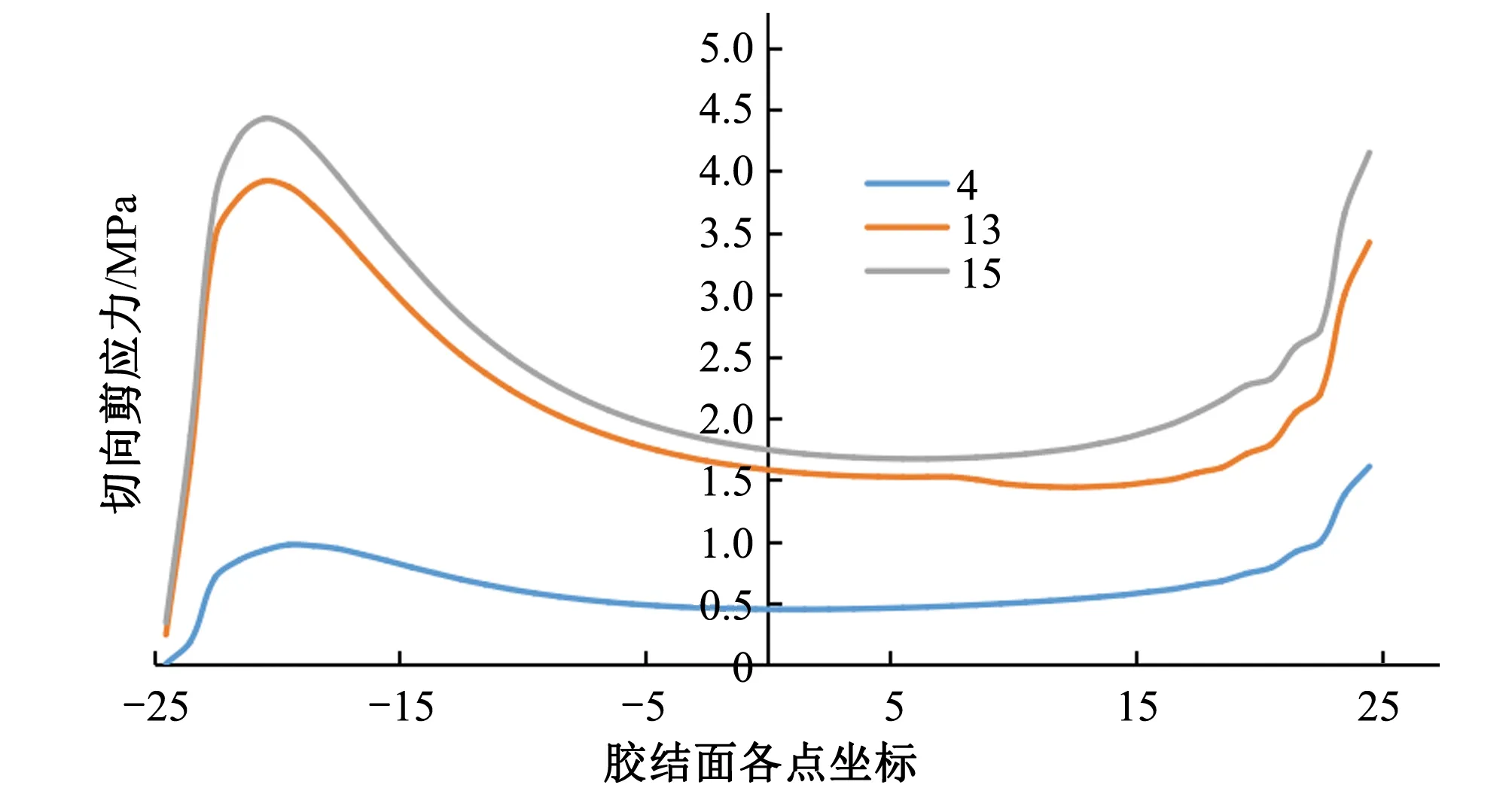
图17 CDP-S不同平均剪应力下胶结面的切向剪应力分布
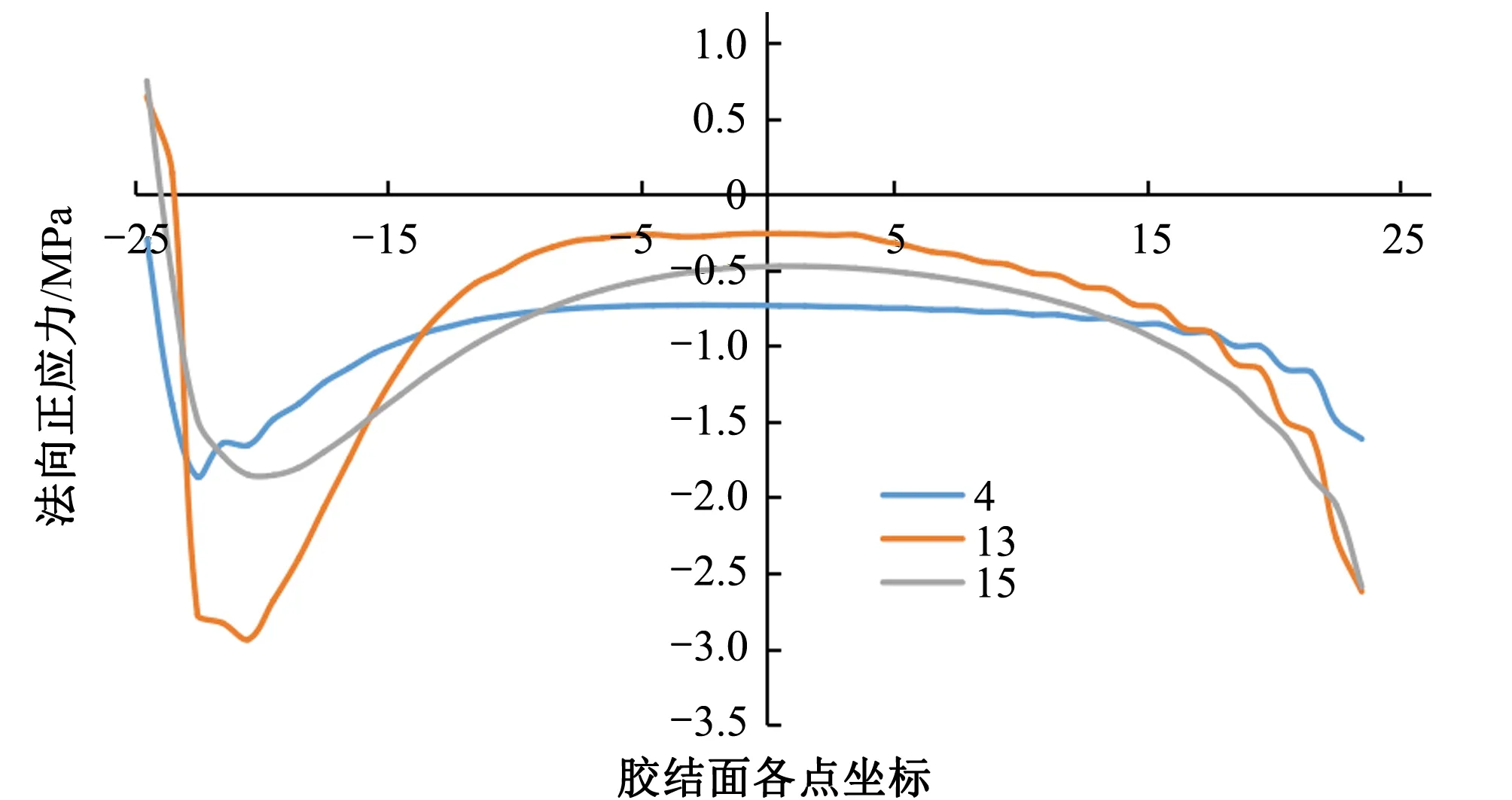
图18 CDP不同平均剪应力下胶结面的法向正应力分布
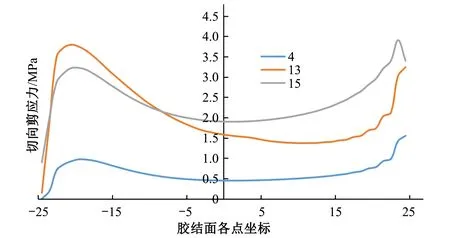
图19 CDP不同平均剪应力下胶结面的切向剪应力分布
当平均剪应力为4MPa时,各材料模型的胶结面仍处于弹性阶段,不同材料模型胶结面的法向正应力分布和切向剪应力分布规律几乎相同,胶结面大约80%的区域应力均匀分布,仅在胶结面首尾两端稍微有些应力集中。
随着平均剪应力逐渐增大,各材料模型的胶结面上的应力分布均越来越不均匀,两端应力集中现象愈发明显。随着推力荷载的增加,JOINT胶结面法向正应力不变的区域其切向剪应力也不变,说明了JOINT破坏方向的唯一性;M-C和CDP-S法向正应力变小而切向剪应力变大,说明了该点处的破坏方向与剪切方向不一致,也体现了M-C和CDP-S各向同性的性质;CDP应力集中处的应力数值反而减小的规律体现了CDP材料应变软化的性质。
3.2.3 剪力位移曲线
图20和图21分别是不同材料模型胶结面上、中、下3个测点的平均剪应力-切向位移关系曲线和平均剪应力-法向位移关系曲线。
从图20中可得,不同材料模型在相同测点处的平均剪应力-切向位移关系曲线大致相同,所有测点的切向位移随外荷载的增加先呈线性缓慢增加,说明在该阶段该测点还未屈服,随后切向位移的增长速率增大,切向位移快速发展。不同材料模型之间在平均剪应力-切向位移关系曲线上的差别仅体现在切向位移发展的速率上,容易发现,M-C和CDP-S测点的切向位移随外荷载呈曲线光滑增长,而JOINT和CDP测点的切向位移曲线有十分明显的拐点,切向位移近似成折线增长。
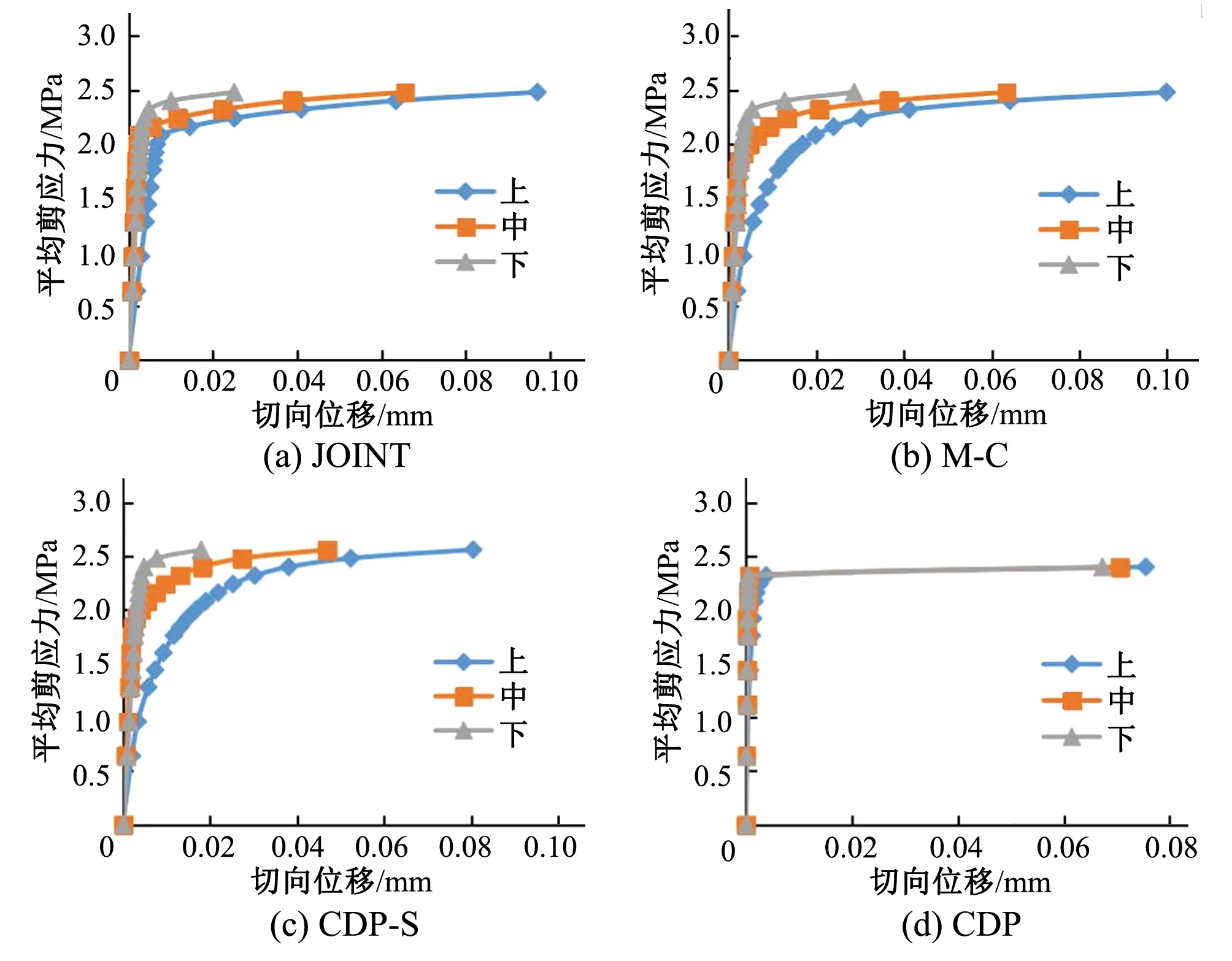
图20 不同材料模型胶结面上、中、下3个测点的平均剪应力-切向位移关系曲线
从图21中可得,不同材料模型下相同测点的平均剪应力-法向位移关系曲线大致相同。在曲线拐点之前(测点屈服之前),测点的法向位移与胶结面平均剪应力近似呈线性关系,法向位移增长缓慢;超过拐点之后(测点屈服之后),位移发展迅速,CDP的拐点最为突出。
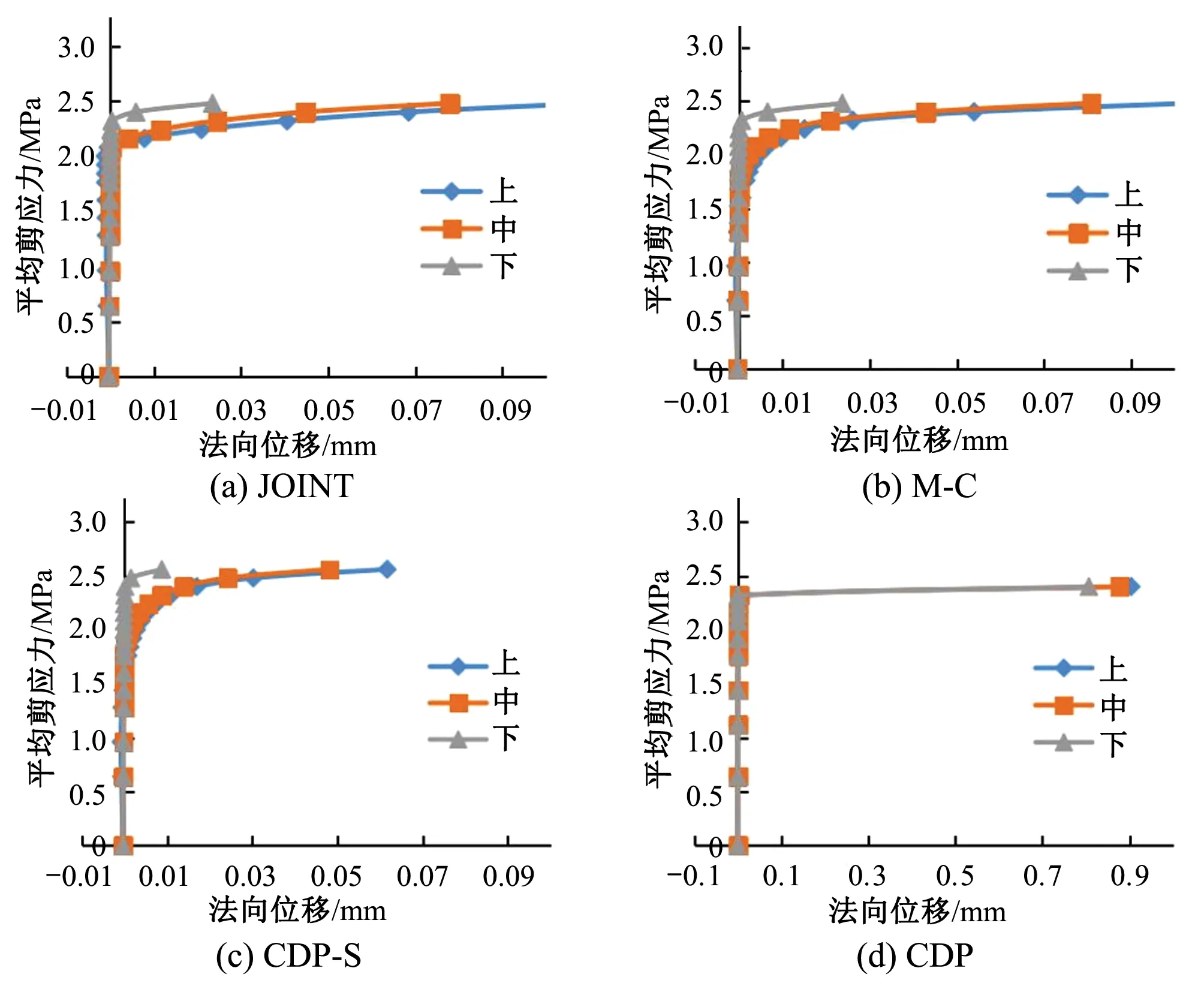
图21 不同材料模型胶结面上、中、下3个测点的平均剪应力-法向位移关系曲线
不同测点的平均剪应力-切向位移曲线和平均剪应力-法向位移曲线也不完全相同,上游测点的位移(切向位移和法向位移)发展相对更加平缓且在相同的外荷载下位移更大。表3是不同测点平均剪应力-位移关系曲线拐点所对应的平均剪应力,从表3也可以看出,除CDP外,其他材料模型的上游测点拐点所对应的平均剪应力最小,下游测点拐点所对应的平均剪应力最大,体现了不同测点的屈服并不同步,也说明了胶结面的屈服区从上游向下游发展的规律。CDP材料模型各测点的拐点对应的平均剪应力相同,超过该拐点,位移迅速增加,材料应变软化的性质导致了胶结面屈服区和位移的突变。
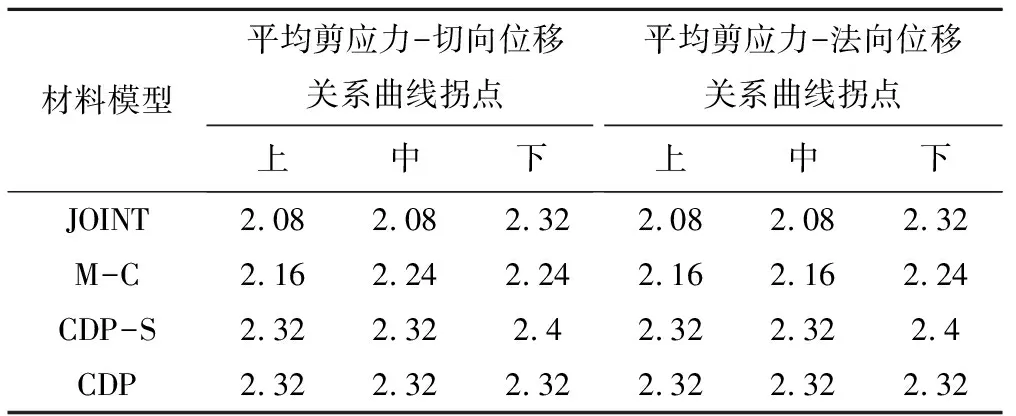
表3 不同测点平均剪应力-位移关系曲线拐点所对应的平均剪应力 MPa
图22给出了重庆鱼嘴长江大桥锚碇混凝土/基岩胶结面抗剪强度试验τN1组应力与位移关系曲线[12]。将数值计算结果(图20,图21)与实际工程试验结果(图22)相比,两者的切向位移发展规律和法向位移发展规律大致相同,说明数值计算结果比较合理。
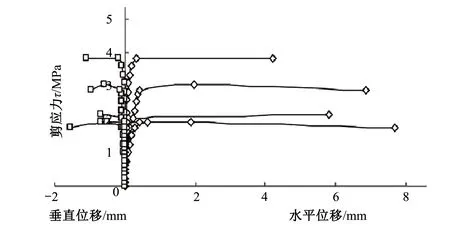
图22 重庆鱼嘴长江大桥锚碇混凝土/基岩胶结面抗剪强度试验τN1组应力与位移关系图
3.2.4 胶结面破坏分析
图23至图27为平均正应力为1 MPa时的计算结果。图23为不同材料模型胶结面屈服区比例随外荷载(平均剪应力)增长的发展曲线。图24-图27为不同材料模型胶结面的屈服区发展云图(红色为屈服区,蓝色为未屈服区)。
从图23可得,M-C、CDP-S和CDP胶结面屈服区比例的发展曲线大致相同,当平均剪应力为0.64 MPa时,胶结面开始出现破坏,随外荷载的增加,屈服区发展相对平缓,最终在平均剪应力为2.5 MPa屈服区比例达到100%,其中CDP胶结面屈服区比例在破坏后期发生突变,从72%直接增长到100%;JOINT胶结面屈服区比例的发展曲线较其他材料模型胶结面屈服区比例的发展曲线差别较大,在平均剪应力为1.28 MPa时,胶结面才开始发生破坏,且曲线存在拐点,平均剪应力超过该点后,屈服区快速发展,最终也在平均剪应力为2.5 MPa左右达到100%。
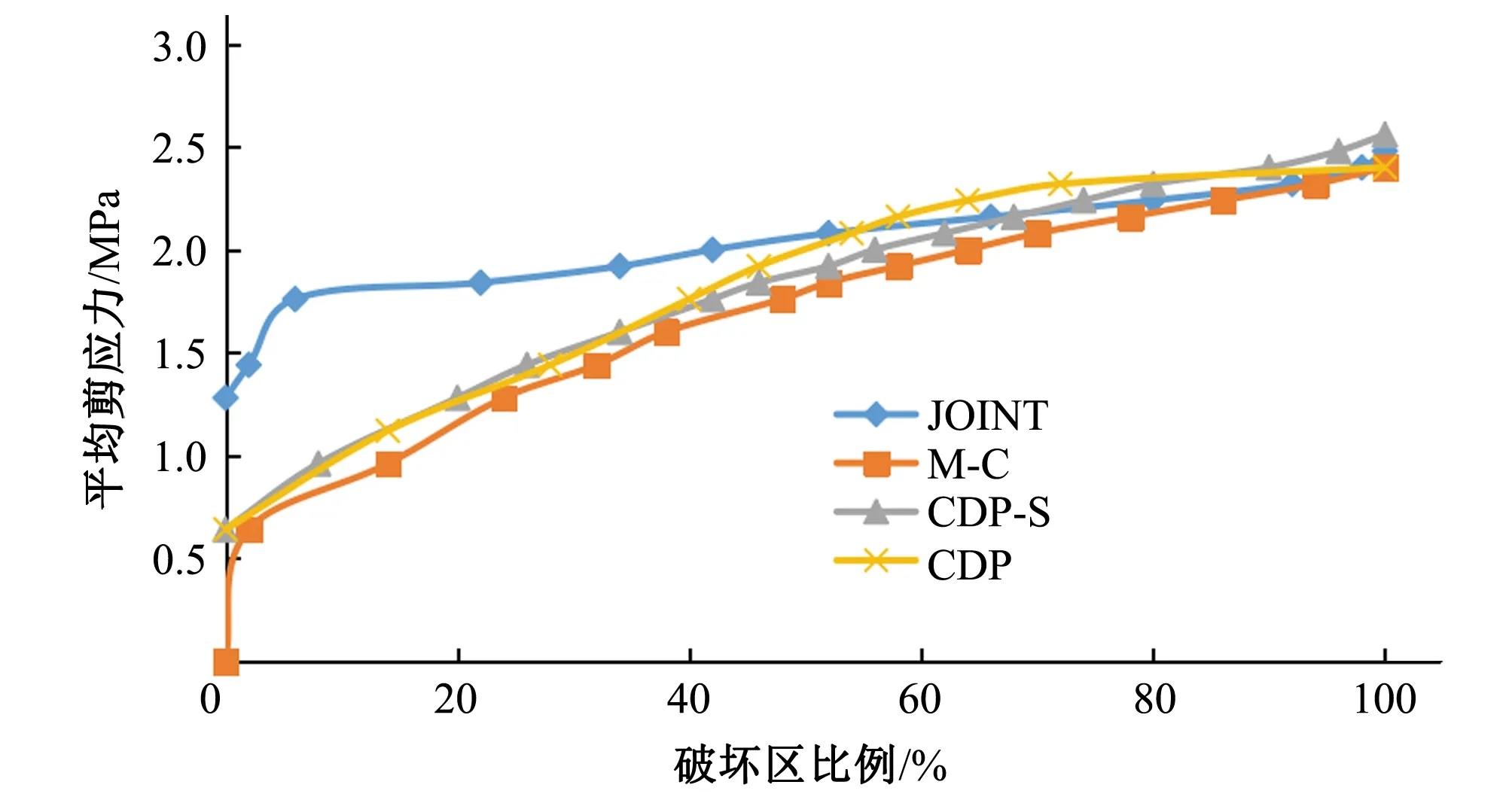
图23 胶结面屈服区比例
从图24至图27可得,不同材料模型下的胶结面屈服区的发展规律大致相同,均从上游逐步向下游发展,直至贯通整个胶结面。

图24 JOINT胶结面的屈服区发展云图

图25 M-C胶结面的屈服区发展云图

图26 CDP-S胶结面的屈服区发展云图

图27 CDP胶结面的屈服区发展云图
4 结 论
本文通过有限元法模拟混凝土/基岩胶结面的现场抗剪试验,分析了不同材料模型下胶结面的应力、位移及屈服区的分布及发展规律。研究结果表明:
(2)通过不同材料模型计算得出的胶结面应力分布规律大致相同,胶结面应力均呈现不均匀分布状态,上下游端部应力集中明显。
(3)通过不同材料模型计算得出的胶结面屈服区发展规律大致相同,随外荷载增加,胶结面屈服区均从上游逐渐向下游发展,直至贯通整个胶结面。
(4)《水利水电工程岩石试验规程(SL264-2001)》[8]中规定通过绘制测点在各法向应力下的剪应力与剪切位移及法向位移关系曲线来确定混凝土/基岩胶结面在各法向应力下的抗剪断强度峰值,这种方法假设了测点处的破坏代表了整个胶结面的破坏,即假设了胶结面的应力分布为均匀分布。由于胶结面的应力分布并不均匀,所以实际上测点处的破坏并不能代表整体破坏,有可能胶结面并没有完全破坏,因此笔者认为通过平均应力整理出来的抗剪强度是偏保守的。
□
