基于Ergun方程的微灌砂颗粒形状系数测定方法研究

2020-12-17李景海翟国亮刘清霞李国强

节水灌溉 2020年12期

李景海，翟国亮，刘清霞，李国强

(1.安阳工学院土木与建筑工程学院，河南安阳 455000；2. 中国农业科学院农田灌溉研究所，河南新乡 453002；3. 安阳市第一中学，河南安阳 455000)

0 引言

在微灌系统中，砂过滤器因其良好的过滤效果而得到广泛应用[1]，由于石英砂具有较稳定的物理性能和化学性能，因而通常将其作为砂过滤器的过滤介质。董文楚[2]对砂滤层过滤机理和堵塞过程进行了分析；Yunkai Li[3]等提出机械过滤是防止灌水器堵塞的主要方法之一；Wenquan Niu[4]等对砂滤层物理堵塞做了进一步研究；翟国亮[5,6]等配制粉煤灰水进行过滤，研究了过滤出水浊度的变化规律；邓忠[7]等配制含沙水进行过滤，对出水浊度与出水粒径级配进行了分析；Tarjuelo[8]等提出砂过滤器在节水的同时，也应注重节能，从而为下游管网提供充足的水压；Mesquita[9]等对砂过滤器水头损失的影响因素进行了分析；Arbat[10]等建立了砂过滤器滤帽水头损失数学模型。Bové[11,12]等研制了一种新型滤帽，并对过滤器水头损失进行了模拟；Jegattheesan[13]等对杂质沉积方程进行了研究；张杰武[14]等自行配制黄河水，对砂滤料过滤水头损失、出水浊度等性能进行了测试；蔡九茂[15]等对砂过滤器水动三向阀性能开展了对比试验；Holtman[16]等采用生物砂过滤系统对葡萄酒厂废水中的有机物去除和pH值中和进行了研究。目前研究多将滤层视为一个整体，而对滤料颗粒形状特征的研究很少。

笔者将砂颗粒近似为理想球体，对砂滤层清洁压降进行了研究，计算出了最佳过滤速度[17,18]，并对砂滤层的反冲洗进行了三维模拟，得出了合理的反冲洗速度范围[19-21]。但由于没有考虑砂颗粒形状对过滤效果的影响[22]，得出的理论值与试验值尚有一定误差。董文楚[23]将砂颗粒形状系数定义为砂颗粒不规则粒径(即筛分直径)与等体积球体直径的比值，并进行了相关研究。由于不规则砂颗粒具有三维尺度，筛分时得到的筛分直径具有随机性，因而对形状系数会造成一定误差。

为了消除砂颗粒空间维度对形状系数测量的影响，笔者在前期研究的基础上，借鉴相关领域研究成果，引入砂颗粒形状系数新定义，该定义采用砂颗粒等比外表面积当量直径代替筛分直径。将砂滤层视为多孔介质，建立了滤层多孔介质阻力压降方程。提出了砂颗粒形状系数的测定方法，即通过砂滤层清水过滤试验测定滤层阻力压降，进而由阻力压降方程确定滤料颗粒形状系数，为砂颗粒测量方法标准[24]的编制提供理论依据，为砂滤料的选型和加工提供技术参考。

1 微灌石英砂颗粒形状系数测定原理

1.1 微灌砂颗粒形状系数计算方法

砂滤层阻力压降与砂颗粒表面积关系密切，砂颗粒与流体接触面越大，则阻力压降越大，为了体现砂颗粒表面积对阻力压降的作用，本文采用与砂颗粒等体积的球体外表面积与砂颗粒外表面积的比值[25-27]作为微灌石英砂颗粒的形状系数，即：

(1)

式中：φ为形状系数，无量纲；S0为砂颗粒外表面积，m2；S为与砂颗粒等体积的球体外表面积，m2。

与砂颗粒体积相等的球体的外表面积表示为：

S=πd2

(2)

式中：d为等体积圆球当量直径，m。

等体积圆球体积公式为：

(3)

式中：V为砂颗粒体积，m3。

由式(2)、(3)可得：

(4)

式中：符号同上。

等比外表面积当量直径定义[28]为：

(5)

式中：符号同上。

由式(1)、(4)和(5)得：

(6)

即石英砂颗粒形状系数也可表示为等比外表面积当量直径与等体积圆球当量直径比值。由于砂颗粒外表面积无法测量，故通过测定滤层阻力压降来计算砂颗粒等比外表面积当量直径，进而计算砂颗粒形状系数。

1.2 石英砂滤层阻力压降方程

液体在固体多孔介质中流动时，液相动量方程为[29]：

式中：t为时间，s；ε为滤层孔隙率，无量纲；p为动压力项，Pa；ρ为流体密度，kg/m3；v为流体在孔隙内的流速，m/s；Ff为作用在流体上的体积力，N。

砂滤层过滤过程中，液相流动为稳定流，且流体仅沿滤层厚度方向流动，因此流速不随时间变化，且在流动方向上不存在梯度，即式(7)左边为0。

体积力由液相压力项、液相黏性项和液相惯性项组成[30]

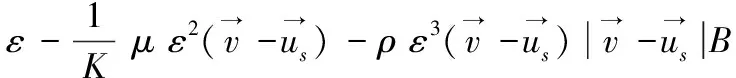
(8)

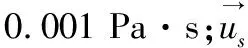
(9)

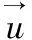
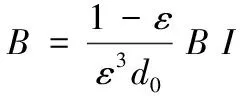
(10)

式中：B为惯性阻力系数，无量纲；I为单位应力张量，在仅考虑流体流动方向时，为1；K为渗透率张量系数，表达式为：

(11)

式中：A为黏性阻力系数，无量纲。

将式(9)、(10)和(11)代入式(7)得多孔介质内流体流动的阻力压降方程，其表达式为：

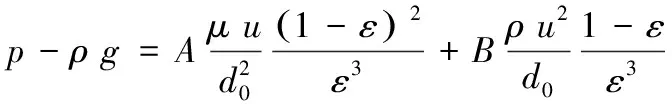
(12)

式中：右边第一项为黏性阻力项，第二项为惯性阻力项；当石英砂滤层进行清水过滤时，砂颗粒表面会形成一层水膜，使砂颗粒表面保持光滑，因此，A取180，B取1.8[31]。式左边为流体的压力梯度，可表示为：

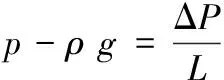
(13)

式中：ΔP为滤层总压降，kPa；L为砂滤层厚度，m。

由式(12)和(13)得Ergun型方程[32]：

(14)

引入雷诺数Re，表达式为：

(15)

对于粒径范围为1.18～1.4 mm的滤层，当Re位于区间[8.4，42]，流体处于过渡流区(液体流态由层流区向湍流区转换时的过渡阶段)；对于粒径范围为1.4～1.7 mm的滤层，当Re位于区间[8.4，68.46]，流体处于过渡流区[17]，在过渡流区，既有层流也有湍流，湍流强度代表速度波动的均方根与平均速度的比值，可用经验公式表示为[33]

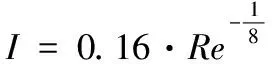
(16)

式中：I为湍流强度，无量纲。

2 微灌砂滤层过滤试验与参数计算

2.1 砂滤层过滤试验

试验在中国农业科学院农田灌溉研究所进行。试验用材料为石英砂，采用由筛分得到的粒径范围为1.18～1.4 mm和1.4～1.7 mm的2种滤层。试验用模型装置如图1所示，过滤器采用透明有机玻璃管制作，管内径200 mm、管高1 200 mm，在其上每隔100 mm高度打1个孔，设为测压取料孔，有机玻管下端安装3个滤帽。石英砂滤料按照自然堆积原则放置于过滤器内部，滤层厚400 mm。试验时，使用水池供水，采用U型压差计测量滤层内部压差，采用涡轮流量计(LWGY-25)测流量，由流量与滤层横截面比值可得水流速度。

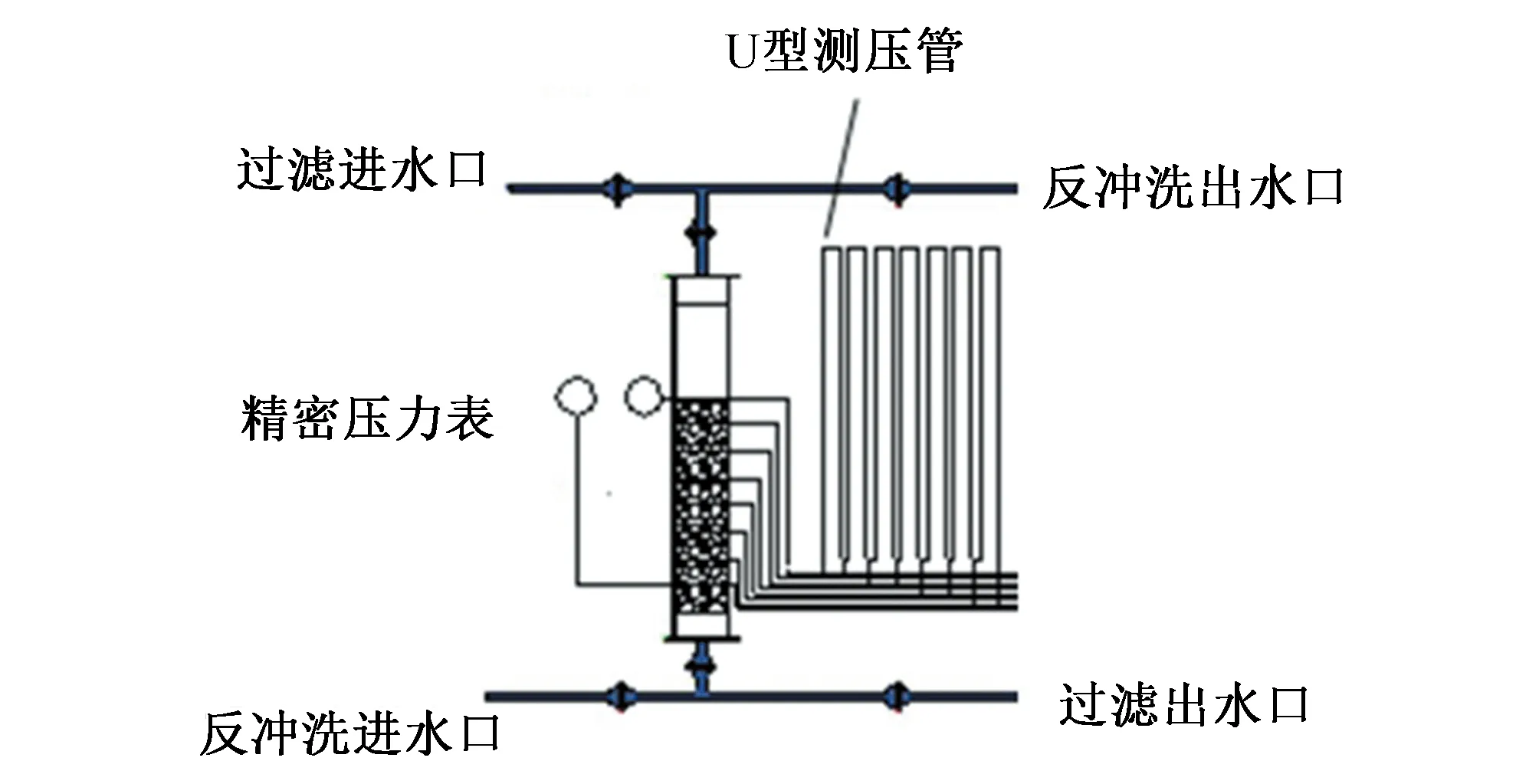
图1 试验装置示意图Fig.1 Schematic diagram of test device

2.2 滤层孔隙率测算

由于石英砂颗粒形状不规则，可以采用注水法测量滤层颗粒间的自由体积，从而计算滤层孔隙率。具体测量步骤：

(1)在容积为500 mL的烧杯内装填石英砂至刻度为500 mL处，装填方法与滤层过滤试验相同，测量滤层与烧杯总质量Msc。

(2)往石英砂孔隙处注水，使石英砂刚好被完全浸没。测量滤层、烧杯和水的总质量Mscw，Mscw与Msc之差即为水的质量Mw，由水的质量得到水的体积。

(3)水的体积与石英砂装填体积(500 mL)的比值，即为滤层孔隙率。

经计算得出，粒径范围为1.18～1.4 mm和1.4～1.7 mm的2种滤层孔隙率分别为0.442和0.444。

2.3 等体积当量直径测算

在粒径范围为1.18～1.4 mm和1.4～1.7 mm的2种滤料中分别随机抽取1 000颗砂粒，用电子天平(梅特勒，ME204E)称出其总质量，得到单个砂粒的平均质量。

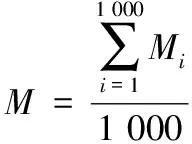
(17)

式中：Mi单颗砂粒的质量，kg；M为砂颗粒的平均质量，kg。

则砂颗粒的平均体积为：

(18)

式中：ρs为石英砂密度，kg/m3，石英砂密度为2 650 kg/m3。

由式(3)、(17)得到砂颗粒等体积当量直径为：

(19)

经计算得到，粒径范围为1.18～1.4 mm和1.4～1.7 mm的2种滤料砂颗粒平均等体积当量粒径分别为1.2 mm和1.5 mm。

3 形状系数计算与分析

3.1 等比外表面积当量直径的计算与分析

在式(14)中，ΔP、ρ、u、L和μ均为已知，因而可计算出等比外表面积当量直径d0。但由于在过渡流区存在湍流，而湍流效应在一定程度上减弱了滤层渗透性能，为了消除湍流效应的影响，采用湍流强度对等比外表面积当量直径计算结果进行修正，得到最终的等比外表面积当量直径dr(见表1)。

dr=d0(1+I)

(20)

由表1可知，随着过滤速度的增加，等比外表面积当量直径呈减小趋势。这是由于当水流流过砂滤层时，在砂颗粒表面会形成一个流动滞缓边界层[34]，随着水流流速的增加，边界层对水流的滞缓作用增强，同时，水流速度的增加，也导致湍流成分的增加，而湍流成分的增加，使能耗和压降快速增加，也在一定程度上减弱了滤层的渗透性能。而根据式(11)，当渗透率降低时，等比外表面积当量直径会随之减小。

同时，随着过滤速度的增加，湍流强度也呈现减小趋势。这是由于在过渡流区，湍流处于发展阶段，随着湍流的不断发展，湍流的稳定性越来越高，则流动速度的波动幅度会越来越小，所以湍流强度会逐渐减小。

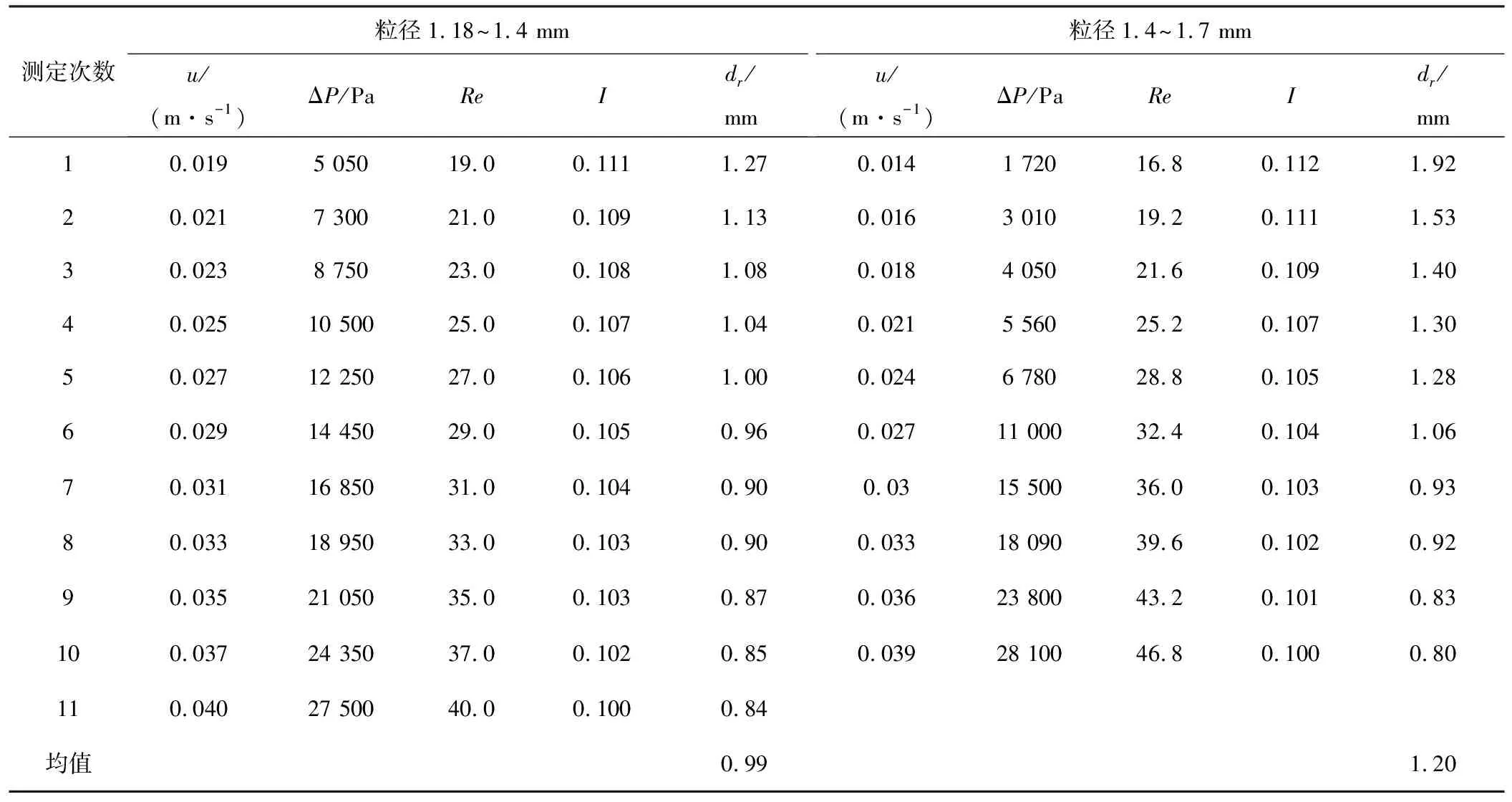
表1 等比外表面积当量直径计算表Tab.1 Specific appearance area-equivalent diameter calculation table

由于湍流的发展会影响滤层渗透性能，需要将湍流对渗透性能的影响控制在一定范围。如果过滤速度太小，则速度和压降的测量将比较困难，如果过滤速度过大，则湍流成分会比较大，将影响到滤层渗透性能的测定。因此，本文以湍流强度为控制指标，湍流强度大于10%时，流体处于高湍流强度区域，说明湍流还没有完全发展，可以作为选取过滤速度的控制范围。