压力式明渠测流装置的数值模拟研究

钟凯月，周义仁

(太原理工大学水利科学与工程学院，太原 030024)>

灌区量水技术可以精确计量进入农田渠系的水量，对节省灌溉用水起着重要作用。传统灌区的量水方法有水工建筑物法、坡降水力半径法、流速面积法等[1]。各量水方法和设备都有其特定的适用范围和条件[2]：水工建筑物量水存在泥沙淤积、建筑物老化的问题，且便捷性差；流速面积法是较常用的量水方法，但市面上的流速仪、超声波流量计等设备价格高昂，不易推广。根据我国目前的量水状况，研发了一种压力式明渠测流装置。该装置不仅成本低、易携带，且测流精度满足要求，具有较高应用价值。

随着信息技术的飞速发展，数值模拟技术在工程上的应用越来越广泛。Fluent软件是市场上占有率最大的CFD软件，可以用来模拟从不可压缩到高度可压缩范围内的复杂流动。流动、传热、化学反应类工程问题都可以用Fluent软件进行分析[3]。为了提高设计效率、检验装置测流精度，采用Fluent模拟软件对压力式明渠测流装置的水力特性进行数值模拟，并进行试验验证。

1 压力式明渠测流装置介绍

压力式明渠测流装置分为水压信号采集部分和机械传动部分。水压信号采集部分集成20个MPX53GP压力传感器，两两一组，均匀布置在如图1所示的10个位置处。每组压力传感器一个正对来流方向，一个垂直来流方向[4]。机械传动部分由不锈钢框架、滚珠丝杠、滑块、步进电机构成。步进电机在单片机的控制下带动滚珠丝杠转动，使水压信号采集部分横向移动，进而测得渠道横断面不同测线的平均流速。

装置的硬件设计分为信号采集模块、数据显示模块、机械传动模块、无线传输模块四部分：信号采集模块负责输出电压信号到单片机；数据显示模块用一块LCD1062液晶显示屏将水流信息以文字、图形形式显示出来；机械传动模块负责水压信号采集部分的水平运动；无线传输模块负责将数据传送到云平台供用户登录查看。装置选用一块24 V的电源供电，如图2所示，各个模块在单片机的调控下进行工作。

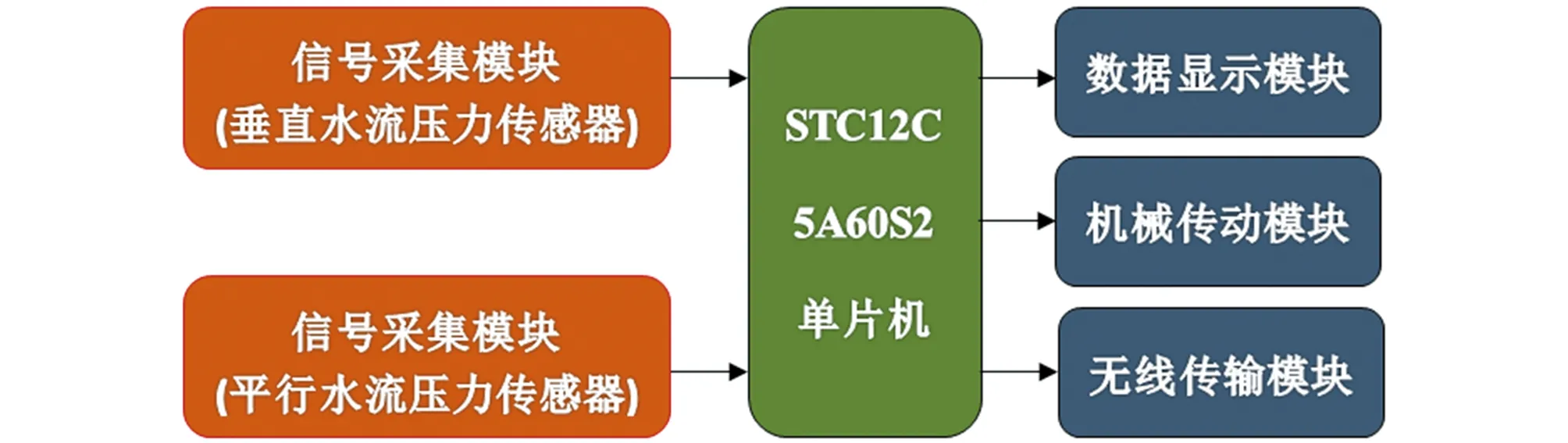
图2 压力式明渠测流装置电气原理框图Fig.2 Electrical block diagram of pressure-type detection device for open channel flow

2 测流原理

压力式明渠测流装置以伯努利方程为基本原理，基于流速面积法进行渠道流量测量[5]。伯努利方程是能量守恒定律在水力学中的一种表现形式，是水力学基本公式之一。伯努利方程是在忽略流体黏性损失的情况下导出的，只适用于不可压缩、无黏性的理想流体。伯努利方程的表达式为：

(1)

(2)

式中：P、P1、P2为流体所受到的压强，Pa；ρ为流体密度，kg/m3；v、v1、v2为流体的流速，m/s；g为当地重力加速度，m/s2；h、h1、h2是流体所在的高度，m；C为常量。

在式(1)中，第一项代表流体的压力势能，第二项代表流体动能；第三项代表流体的重力势能。三项和为一常数，表明在不可压缩理想流体中各种机械能可以相互转换，但流体的总机械能沿流程不变。式(2)则表明流体沿流线运动过程中任意两点的机械能相等。

压力式明渠测流装置正对水流的压力传感器流速为v1，垂直水流的压力传感器流速v2=0。每组压力传感器位于同一高度，故h2=h1。依据公式(2)得：

(3)

整理得：

(4)

由式(4)可知，每组压力传感器压差与该位置处流速呈一一对应关系，流速可以根据该位置处压力传感器压差计算得到。

流速面积法根据过水断面面积和断面上的流速分布计算渠道的流量。本系统中，步进电机带动滚珠丝杠使水压信号采集部分横向移动到达过水断面的各条测线。水面淹没下的压力传感器组可获取对应水深点的流速。流速在过水断面上的空间平均值乘以断面面积即可得出流量值。

3 试验过程

3.1 试验工具

为了验证压力式明渠测流装置的测流精度，在太原理工大学水利科学与工程学院的水流大厅矩形渠道上进行了验证试验。试验所需工具包括压力式明渠测流装置一套、笔记本电脑一台、电磁流量计一个。

3.2 试验步骤

图3为测流试验系统示意图，供水系统由地下水库和离心泵构成，流量调节系统由两个调节阀和一台电磁流量计构成。水从地下水库抽出经输水管到稳流池1，再从稳流池1流入U型渠道，经稳流池2稳定后流入矩形渠道。压力式明渠测流装置放置在矩形渠道上方进行测流。

打开水泵，启动测流装置，待来流稳定后打开上位机开始监测。试验过程中电磁流量计进行同步测流。本次试验选取了3个流量：390、215、120.7。390 m3/h时淹没七个传感器测点，215 m3/h时淹没5个传感器测点，120.7 m3/h时淹没4个传感器测点。分别计算3种工况下过流断面流速空间平均值，乘以过水断面面积得到流量值。记录测量数据，作为模拟结果的对照。

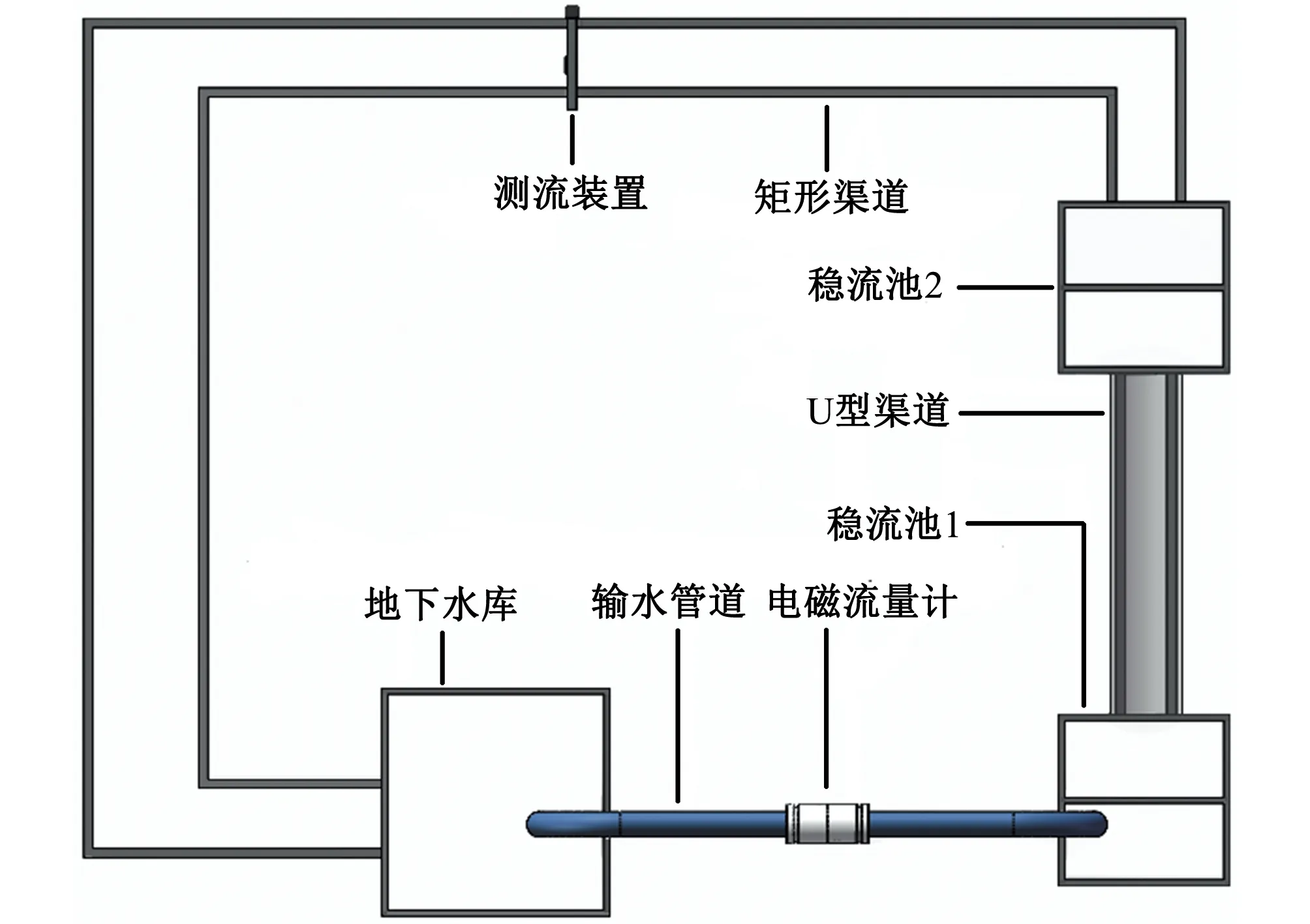
图3 测流试验系统示意图Fig.3 Schematic diagram of flow test

4 数值模拟过程

4.1 几何建模与网格划分

试验渠道宽0.53 m，深0.6 m，底坡为1/1 000。压力式明渠测流装置的水压信号采集部分为长0.47 m、直径0.06 m的圆柱结构。为充分模拟水流在矩形渠道的流态，同时缩短模拟时间，渠道的建模长度选为3 m。水压信号采集部分位于渠道正中央，选取底部圆心处为坐标原点，水流方向为Z轴正方向，重力方向为Y轴负方向，顺水流方向左侧为X轴正方向。模型图如图4所示。

图4 系统建模示意图Fig.4 Schematic diagram of system model

在流体计算软件中经常用到计算网格，计算网格的核心原理是将模型空间的计算区域分割成足够小的计算区域，然后用流体控制方程求解，最后得到全部计算区域上的物理量。从数学的角度，网格划分越密集计算的精度越高，然而实际上计算精度和网格的数量不是线性增长关系，且网格越密集，需要的计算资源越大，计算的时间也越长。所以网格划分尺寸要结合实际综合考虑。压力式明渠测流装置的最大尺寸是渠道的长度，为3 m，最小尺寸为0.06 m。非结构化网格对于细节的捕捉好，适应性强，为了保证计算的精度和网格的质量，网格划分采用非结构化网格，最大尺寸为2.5 cm，网格总数约为52万个。网格划分示意图如图5所示。

图5 网格划分示意图Fig.5 Schematic diagram of mesh

4.2 边界条件

明渠流动是有明显分界面隔开的非混合流体(空气和水)流动，自由水面问题的研究方法主要有：刚盖假定法、弹性盖法、高度函数法(HOF)、标记网格法(MAC)法、体积率法(VOF)和等值面函数法等各种方法[6]。自由液面的处理采用VOF模型。VOF多相流模型通过求解一套动量方程和跟踪穿过计算域的每一种流体的体积分数来模拟两种或多种不能混合的液体，在明渠、水坝水流、灌注、晃动等多种问题上具有很好的适用性和准确性[7]。在气液两相流中，VOF模型的描述公式如下所示。

qa(x,y,z,t)+qw(x,y,z.t)=1

(5)

(6)

式(5)中，等号左侧第一项、第二项分别表示空气和水在某时刻某单元格的体积分数，两者都是时间和空间的函数，在每个单元格内两相体积分数和都是1。式(6)为液相水的体积函数控制方程，液相水的体积分数随着时间和空间的变化而变化，所以计算时需要采用瞬态求解方法。

边界条件是流场变量在计算边界上应该满足的数学物理条件，边界条件和初始条件一起被称为定解条件，定解条件确定后流场的解才唯一存在。Fluent软件在初始化过程中即完成初始条件的设定，边界条件需要单独设置。边界条件设置如下：上游入口设置为速度入口，利用平均流速控制瞬时流量大小；下游出口设置为压力出口；渠道的顶部为压力入口；参考压强为大气压；渠道两侧边壁、渠道底部、水压信号采集部分均设置为无滑移固体边壁，粗糙度常数设置为0.5。

4.3 求解方法

流体模拟实质上是求解一系列偏微分方程，用数值方法求解偏微分方程时需要将方程离散化，即将计算域内的网格节点或者网格控制体中心点上的因变量作为未知量来处理，从而建立一系列关于这些未知量的代数方程。Fluent中常用的离散化方法有有限差分法、有限元法、有限体积法和有限分析法。有限差分法在规则的结构化网格上简单有效，但在不规则区域的适应性不如有限体积法，离散方程的守恒特征也难以保证。有限元法在对流项的离散处理方面不如有限体积法成熟。故求解方法采用有限体积法，有限体积法也是目前应用最普遍的一种数值方法。

有限体积法是对一般形式的控制微分方程在控制体积内进行积分，即求解积分形式的守恒方程，该方程如下所示：

(7)

式中：Φ为广义上的变量，可以是速度、温度、压力等待求解的物理量；Γ是对应Φ的广义扩散项。等号左侧第一项表明变量Φ的总量在控制体积内随时间的变化量，第二项表明变量Φ因对流而引起的沿控制体表面外法线方向n的流出率。等号右侧第一项是扩散项的积分，它的物理意义是控制体内变量因扩散引起的净增加量，第二项是源项的积分，它的物理意义是控制体内由于产生、耗散或其他原因源项引起的变量净增加量。

控制方程离散化之后可以进行求解，Fluent模拟软件提供了压力基求解器和密度基求解器两种。密度基求解器可用于高速可压缩流体，本系统采用压力基求解器即可。在算法选择上选择PISO算法，PISO算法是典型的两步校正算法，常用于网格偏斜严重或非定常流动状况。紊流模型选择Realizablek-ε模型，运行计算时，每10步保存一次。

5 结果分析

5.1 水面分析

水面是模拟明渠流动时的一项基本研究对象，通过对比模拟结果和试验现象可以判断模拟的结果是否符合实际。图6是流量为390 m3/h时水流在渠道内流动的水面图，从上向下依次为计算500 步、1 000 步、2 500 步时的水面图。观察发现，水流在流入渠道时水位逐渐上升，由于测流装置阻隔，在装置下游区出现涡旋。随着水流不断涌入渠道，水位不断升高，达到一定高度后水位趋于稳定。与试验现象吻合。

图6 计算500、1 000、2 500步时的水面图Fig.6 Schematic diagram of water surface at 500、1 000 and 2 500 steps

5.2 精度分析

数值计算数据每10步保存一次，保存的数据对应着计算域内每个网格的物理量。将数据导入后处理工具CFD-POST，在装置的压力传感器处创建观测点可以得到该处的压强值，依据公式(4)计算各点流速。将模拟数据和试验数据进行对比，表1～3是在390、215、120.7 m3/h 3种工况下的流速对比结果。表4是3种工况下的流量对比结果。

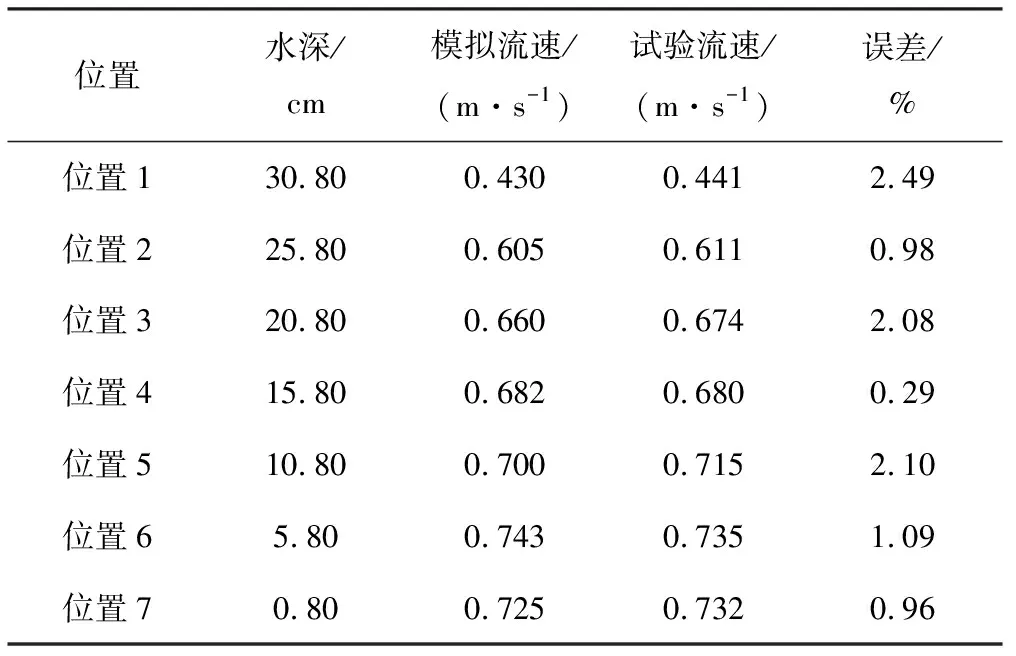
表1 Q=390 m3/h时的流速对比和误差Tab.1 Comparison and error of velocity at Q=390 m3/h

表2 Q=215 m3/h时的流速对比和误差Tab.2 Comparison and error of velocity at Q=215 m3/h

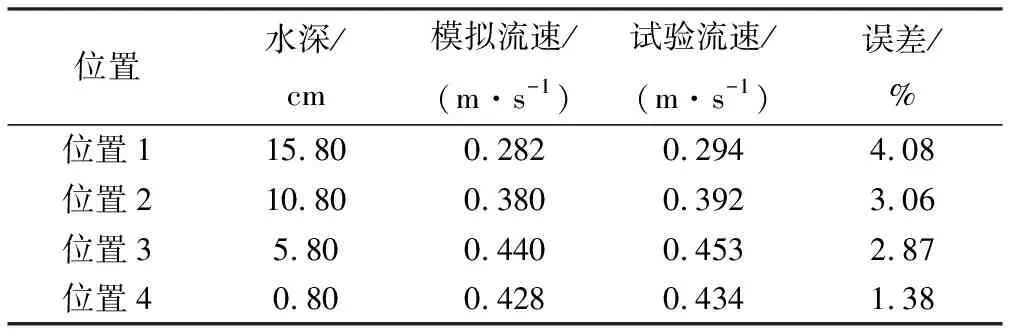
表3 Q=120.7 m3/h时的流速对比和误差Tab.3 Comparison and error of velocity at Q=120.7 m3/h

表4 模拟流量与试验流量对比和误差Tab.4 Comparison and error between simulated flow and test flow

由表1～4数据可知，3种工况下数值模拟的流量误差不超过5%，满足测流精度的要求，证明了压力式明渠测流装置数值模拟的可行性。

从表4可以看出该装置的流量测量值与电磁流量计的测量值相差较小。原因可能在于渠道内或水流里残存的杂质对传感器存在一定的影响，此外明渠水流的过快或过慢也会影响装置的测流精度。数值模拟的流量值和试验流量间也存在差别。主要原因可能是测流装置建模同实物间有细微的差别，计算时水流的密度选择了恒定值，没有考虑到地下水库的水流含有些许杂质。

6 结 语

压力式明渠测流装置适用于宽度不超过1.5 m的矩形、U型、梯形渠道，在使用时可以根据实际情况调整装置的安放位置。利用Fluent软件对压力式明渠测流装置在底坡为1/1 000的矩形渠道下进行数值模拟，通过模拟数据和试验数据的对比分析得到了以下结论：

(1)采用VOF两相流模型和Realizablek-ε模型对矩形渠道内测流装置水力特性的数值模拟表明：来流过程中水面线逐渐升高，最终趋于稳定；水流在装置下游区出现涡旋；自由液面横向流速从渠道中心到渠道两侧边壁逐渐减小，中心断面垂向流速从渠道底部到自由液面先增大后减小，最大流速点位于自由液面以下某一位置。

(2)数值计算得到的流速值、流量值与试验数据的误差小于5%，满足测流精度的要求。为不同工况下的测流模拟提供了可靠度，可节省大量的户外试验时间。

(3)压力式明渠测流装置由点流速到线流速再到面流速实现了断面流速的多点测量，降低了人力投入，具有良好应用前景。