带噪声水平评估的快速灵活盲深度降噪模型

于海雯,易昕炜,徐少平,林珍玉

(南昌大学 信息工程学院,南昌 330031)

0 概述

近年来,受图形处理单元硬件支持的深度卷积神经网络(Deep Convolutional Neural Network,DCNN)被证明具有强大的特征学习和非线性映射能力,将其应用于图像降噪领域后,在执行效率和降噪效果2个关键评价指标上相对于传统降噪算法具有明显优势[1-3]。

目前,IRCNN(Image Restoration CNN)[4]、DnCNN(Denoising CNN)[5]、UDNet(Universal Denoising Network)[6]和FFDNet(Fast and Flexible Denoising Network)[7]等基于DCNN的主流降噪模型,克服了传统降噪算法依赖人工提取图像先验知识的缺点,在改善降噪效果的同时大幅提高了算法的执行效率。上述模型在本质上都是基于数据驱动(data-driven)策略实现的,通过在大量数据集上进行训练,端到端学习噪声图像与无失真图像或残差图像(噪声图像与无失真图像之间的差图)之间复杂的映射关系,从而实现噪声图像的高质量复原。

以DnCNN降噪模型为例,该模型以噪声图像及其对应的残差图像作为深度卷积神经网络的输入-输出训练对(Training Pairs,TP),通过训练实现一个降噪效果好且执行效率高的高斯降噪模型。然而,受技术路线的内在制约,基于DCNN网络构建的DnCNN等降噪模型的降噪性能在很大程度上依赖于训练图像集,只有在待降噪图像的噪声水平值与训练降噪模型所用图像集的噪声水平值相一致或近似的条件下,才能获得最佳的降噪效果。DnCNN模型需要针对给定噪声图像的噪声水平值,调用专门针对这一噪声水平值训练的降噪模型,才能获得最佳的降噪效果,这意味着在噪声水平值变化范围内需要训练多个降噪模型。为解决该问题,FFDNet降噪模型[7]调整了DnCNN网络模型的输入结构,除输入噪声图像外,还增加了噪声水平映射图(Noise Level Map,NLM)作为辅助输入通道。引入的NLM映射图与噪声图像大小相同,但噪声水平图中各个点的亮度值为噪声水平值。经过训练后所获得的FFDNet降噪模型中的网络参数不再依赖图像噪声水平值,这意味着只需训练一个降噪模型就可处理任意噪声图像的降噪问题。此外,FFDNet降噪模型在网络模型的输入端和输出端分别设置下采样和上采样模块,这种结构有助于提高模型的降噪效果和执行效率。与DnCNN等深度降噪模型相比,FFDNet模型具有更好的降噪能力、更快的执行速度以及更高的灵活性,但是发挥这些优越性能的前提是FFDNet降噪模型需要以待降噪图像噪声水平值生成的NLM映射图作为网络模型的输入数据,模型性能取决于能否准确地对待降噪图像中的噪声水平值进行测定。

对给定噪声图像的噪声水平值进行准确测定的方法称为噪声水平估计(Noise Level Estimation,NLE)算法[8-10]。对于NLE算法而言,估计准确性是衡量其性能的重要评价指标。为获得较准确的估计结果,ZORAN等人[11]利用自然图像经DCT(Discrete Cosine Transform)变换后所得到的边缘带通系数的峰度(Kurtosis)统计值具有尺度不变的特性,通过构建目标优化函数并迭代搜索目标函数最优值来估计噪声图像的噪声水平值。ZORAN所提算法在中、低噪声水平下具有较好的预测准确性,但是在高水平噪声条件下预测性能下降。此外,该算法执行时间较长,在目标寻优过程中可能失败。为此,DONG等人[12]综合利用带通域上Kurtosis值的分段平稳性和正则性,将噪声水平估计问题转化为迭代优化拟合Kurtosis模型的问题。DONG所提算法能够准确地估计图像噪声水平值,但其执行效率仍然较低。

GUPTA等人[13]利用DCT滤波响应的局部对比度归一化系数分布统计值的尺度不变性,实现了一种NLE算法,其具有较好的预测准确性,但计算复杂度较高。除了利用图像变换后的统计规律构建NLE算法之外,利用图像中同质图块的协方差矩阵对噪声水平值进行估计也是一种常见的NLE方法。FANG等人[14]利用组合系数对协方差矩阵最小特征值和多个冗余维度的特征值进行线性组合,克服了采用最小特征值估计噪声水平值时的不足,在各个噪声水平下都具有较高的估计准确性和鲁棒性,但是,其仍然需要采用迭代的方式来选择同质图块,执行时间较长。综上,现有的多数NLE算法为保证预测准确性而构造复杂的推演过程,导致算法执行效率普遍较低,而作为各种非盲降噪算法的前置模块,NLE算法的执行效率很重要,其效率较低将影响整个降噪过程的执行效率。

为了使得FFDNet降噪模型在实际应用中能获得最佳的降噪效果并保持较高的执行效率,在分析其网络模型结构的基础上,本文建立一种由浅层卷积神经网络(Shallow Convolutional Neural Network,SCNN)和BP(Back-Propagation)神经网络2种串行网络模块构成的NLE模型,并将其作为FFDNet降噪模型的前置模块。采用与FFDNet模型相同的网络架构,但以SCNN网络方式构建噪声分离模型将噪声信号从噪声图像中分离出来,得到粗略的噪声映射图(Noise Mapping,NM)。NM的标准差与真实噪声水平值之间有一定偏差,但鉴于它们之间具有极高的相关性,本文利用预训练的BP神经网络修正模型,将初估值修正为最终的噪声水平值,从而获得一种准确而快速的NLE模型。将该NLE模型与FFDNet降噪模型相结合,使得FFDNet转换为盲降噪模型BFFDNet。

1 FFDNet降噪模型

1.1 模型架构

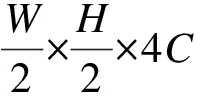
图1 FFDNet降噪模型的网络架构

1.2 模型缺陷

FFDNet降噪模型使用NLM映射图作为辅助信息,有助于提高模型的降噪性能,但仍然需要用户准确地给定σ值的大小才能获得最佳的降噪效果。当设置的σ值与噪声图像中真实噪声水平值不一致时,模型的降噪效果将下降。如图2所示,对原始无失真的Lena图像施加噪声水平值σtrue=40的高斯噪声,使用σtest=10,20,30,40,50,60,70不同的噪声水平值作为FFDNet降噪模型的输入参数分别对该噪声图像进行降噪。从图2可以看出,当设置的噪声水平值σtest小于待降噪图像的真实噪声水平值σtrue时,复原图像中仍然残留了部分噪声,如图2(c)～图2(e)所示,且模型的降噪效果随σtest与σtrue之间差值的增大而降低;当σtest大于σtrue时,复原图像的边缘区域过于平滑,纹理细节丢失,如图2(g)～图2(i)所示,且σtest与σtrue之间的差值越大,模型的边缘保持能力越差;当且仅当σtest与σtrue相等时,模型能够取得最佳的降噪效果,复原图像的PSNR(Peak Signal to Noise Ratio)值为30.25 dB。因此,在实际应用中,采用一个预测准确性好且执行效率高的NLE算法作为FFDNet降噪模型的前置模块,对于保障FFDNet模型的降噪效果十分重要。

图2 不同σtest值情况下FFDNet模型的降噪效果对比

2 基于神经网络的两阶段NLE模型

2.1 问题分析

2.2 本文模型实现策略

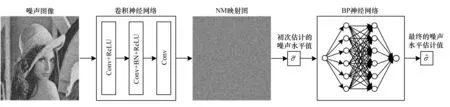
图3 本文NLE模型流程

2.3 噪声水平值初估

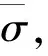
图4 使用不同网络层数构建的初步降噪网络降噪效果对比

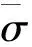
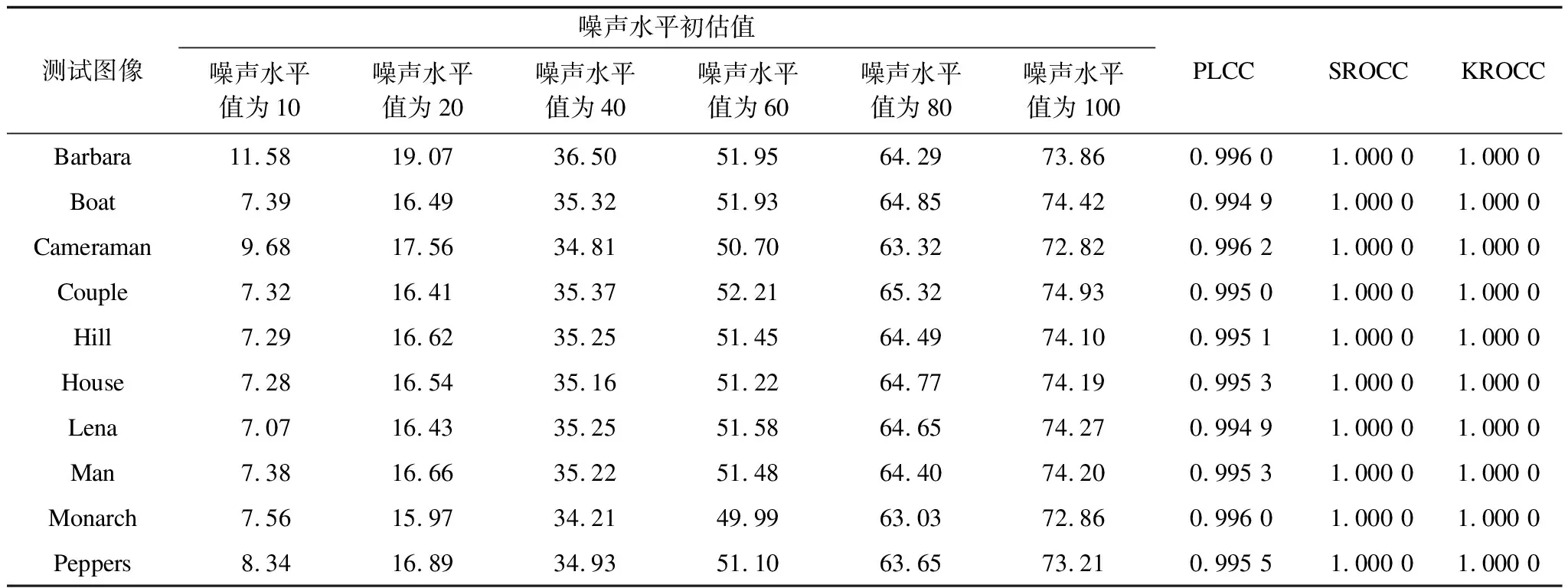
表1 单张图像噪声水平初步估计值与噪声水平真值之间的相关性

表2 多张不同噪声图像噪声水平初步估计值与噪声水平真值之间的相关性Table 2 Correlation between the initial estimated noise level and the true noise level of multiple images with different noises

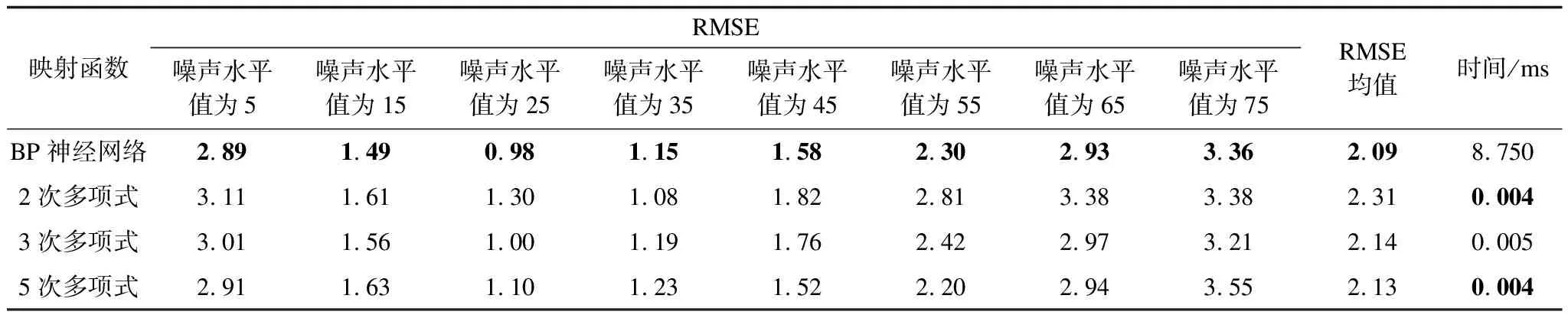
表3 50张BSD图像上噪声水平预测值与真值之间的均方根误差Table 3 RMSE between predicted value and true value of noise level on 50 BSD images

综上,对于一张待降噪图像,本文所提的NLE模型对其噪声水平值进行估计的整个执行过程,只需依靠2个事先训练好的神经网络模型而没有繁琐的迭代过程,执行效率高,这使得其作为FFDNet的前置模型具有一定优势。

2.6 优势分析

与其他NLE算法相比,本文所提NLE模型优点如下:

1)采用预训练的SCNN网络和BP神经网络粗、精相结合,两阶段串行运行即可实现准确的噪声水平值估计,没有过多迭代求解过程,具有较高的执行效率。

2)在模型训练完成后,仅需利用训练得到的网络权重值就可直接将待降噪图像映射为残差映射图,易于使用。

3 实验结果与分析

3.1 测试环境

为了评估本文所提NLE模型的性能,将其与文献[11]算法、文献[19]算法、文献[9]算法、文献[20]算法、文献[13]算法和文献[14]算法共6种代表性NLE算法,在预测准确性、实际应用效果和执行效率3个方面进行比较。测试图像集合是由BSD数据库[17]中的50张图像(不同于NLE模型训练时所使用的图像)构成的纹理图像集,其中,10张具有代表性的图像如图6所示,纹理图像集中的图像内容具有更为复杂的细节特征,适用于测试算法的鲁棒性。所有实验均在统一的环境下完成,硬件平台为CPU Intel®CoreTMi7-6700 @ 3.40 GHz RAM 16 GB,软件环境为Windows 10.0操作系统,编程环境为Matlab R2017b。

图6 BSD数据库中的10张代表性图像

3.2 预测准确性

对BSD数据库中50张图像分别施加噪声水平值为5、15、25、35、45、55、65和75的高斯噪声,然后利用各种对比算法对每张噪声图像的噪声水平值进行估计,计算每个噪声级别下各个算法所获得的噪声水平估计值与真实值之间的均方根误差,结果如表4所示。从表4可以看出,本文NLE模型在所有噪声水平下的均方根误差均值最小,且在各个噪声条件下获得的均方根误差值相差不大,说明其预测准确性更为稳定,且在处理复杂图像内容时具有较高的鲁棒性。

表4 50张BSD图像上各算法噪声水平预测值与真值之间的均方根误差Table 4 RMSE between predicted value and true value of noise level of each algorithm on 50 BSD images

3.3 实际应用效果

为了验证本文所提NLE模型的实际应用效果,将其与FFDNet降噪模型相结合,构建BFFDNet模型,使用噪声水平预测值完成盲降噪任务,并与使用真实噪声水平值的FFDNet降噪模型在常用图像集和纹理图像集2个测试图像集合上进行对比实验。对2个测试图像集的图像依次施加噪声水平值为10、20、30、40、50和60的高斯噪声,计算2个模型在每个噪声比例下复原所有图像获得的PSNR均值,结果如表5、表6所示。从表5、表6可以看出,BFFDNet降噪模型的降噪效果总体上与FFDNet降噪模型相差不大,σtrue=10时差距较大,但在视觉上效果差别较小,当σtrue≥20时两者几乎没有区别,从而有效地验证了本文NLE模型的预测准确性,其估计值可以达到与真实噪声水平值相近的效果。

表5 FFDNet与BFFDNet降噪模型在常用图像集上的PSNR均值比较Table 5 Comparison of PSNR mean values of FFDNet and BFFDNet denoising model on common image sets dB

表6 FFDNet与BFFDNet降噪模型在纹理图像集上的PSNR均值比较Table 6 Comparison of PSNR mean values of FFDNet and BFFDNet denoising model on texture image sets dB

3.4 执行效率

NLE算法作为多种非盲降噪算法的前置预处理模块,其执行效率关系到图像降噪算法的整体性能。为了更全面地评估本文所提NLE模型的执行效率,对大小为512像素×512像素的Lena图像施加噪声水平值为30的高斯噪声,计算各个对比算法估计该图像噪声水平值时的执行时间,结果如表7所示。从表7可以看出,在所有对比NLE算法中,本文NLE模型具有最少的执行时间,其在预测准确性和执行效率2个方面的综合性能最佳,且本文所构建的BFFDNet模型在单张Lena图像上的总执行时间为3.2 s,其中,噪声水平估计模块的执行时间为0.01 s,几乎可以忽略不计,表明FFDNet降噪模型与所提NLE模块相结合后只需花费很少的时间代价便可实现盲降噪,且能获得较好的降噪效果,具有很强的实用性。

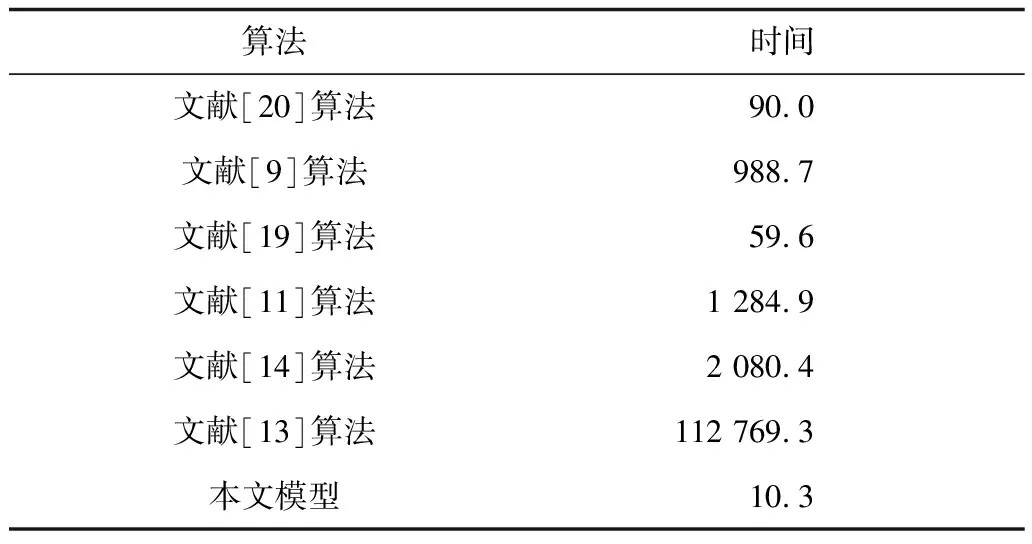
表7 噪声水平值估计的执行时间比较Table 7 Comparison of execution time of noise level estimation ms

4 结束语

引入NLM映射图后的FFDNet仅需训练一个降噪模型即可对具有任意噪声水平值的噪声图像进行降噪,但是其在实际应用中,必须通过准确的噪声水平估计值构建NLM映射图后才能获得最佳降噪效果。为此,本文建立一种基于神经网络的两阶段NLE模型,并将其作为FFDNet降噪模型的前置模块,从而构建BFFDNet盲降噪模型。实验结果表明,该NLE模型具有较高的预测准确性和执行效率,BFFDNet盲降噪模型的降噪效果与原FFDNet降噪模型的最佳降噪效果相近,验证了所提NLE模型的有效性。本文NLE模型除了可以与FFDNet降噪模型相结合外,也可与多数非盲降噪算法兼容使用。下一步考虑将所提噪声水平估计模型中的浅层降噪网络和BP神经网络集成为一个网络,进一步提高模型在训练和应用时的便捷性。