基于随机抽样GMM的城市交通运行状态模式分类

姚博凡,邓红平,蔡 铭

(1.中山大学 智能工程学院,广东 深圳 518106; 2.广东省智能交通系统重点实验室,广州 510006; 3.佛山交通运行监测中心,广东 佛山 528000)

0 概述

在智能交通系统(Intelligence Transportation System, ITS)中,路段交通运行状态模式分类始终是研究者和交通管理部门关注的重点。城市路段交通运行状态模式分类是指按照一定的分类标准,将交通流状态划分为不同的等级,分别代表不同程度的畅通或拥堵情况。相比传统的交通流特征参数(如流量、速度等),交通运行状态更能直观地反映当前路段的交通路况,为交通出行者提供直接的出行参考依据,帮助其制定出行路线,规避交通拥堵,从而提高出行效率,同时也可以分散交通出行量,避免交通拥堵现象进一步恶化。此外,交通运行状态还可以为交通管理者决策提供数据支持,对于城市交通运行具有重要意义。

本文从路网路段全局适用性的角度出发,通过选取合适的聚类指标,从数据中挖掘聚类指标的分布特点,运用高斯混合模型(Gaussian Mixture Model,GMM)对路网的交通运行状态模式进行分类,同时借助分等级抽样聚类的方法,确定能代表路网交通运行状态分布情况的采样路段数,并且给出最合理的交通运行状态分类模式数。在此基础上,将本文方法与模糊C均值聚类(FCM)和K均值聚类(K-means)方法的分类性能进行对比,并对不同模式下的交通运行状态加以分析。

1 相关工作

现有的交通运行状态模式分类方法主要分为以下2类:

1)基于相关标准规范的分类方法。在国外标准方面,比较著名有美国的《道路通行能力手册》[1],其中按照平均行程速度、密度和V/C值对交通流运行状态进行分级评价,共分为6个等级,此外,日本、德国、澳大利亚和新西兰也提出了相应的标准规范[2-4];在国内标准方面,有相应的国家标准《城市交通运行状况评价规范》[5],其中以路段行程速度与自由流速度的比值作为分类指标,将交通运行状态分为5种模式,即畅通、基本畅通、轻度拥堵、中度拥堵和严重拥堵,也有部分城市(如北京、上海、广州等)提出了相应的地方标准[6-8]。

2)基于聚类的分类方法。在以往的研究中,常用的聚类方法包括模糊C均值聚类(FCM)[9-10]、K均值聚类(K-means)[11-12]和高斯混合聚类(GMM)[13-14]。前两种方法的研究较多,而应用GMM开展交通运行状态模式挖掘的研究相对较少。文献[15]以流量、速度和占有率作为聚类指标,运用FCM聚类算法将交通运行状态分为5种模式。文献[16]在流量、速度和占有率的聚类指标基础上,新增了流量富余度这个指标,将其定义为路段的当前流量与最大流量的差值除以最大流量。文献[17]同样基于FCM聚类算法,以流量、速度和占有率作为聚类指标来进行交通运行状态聚类。文献[18]基于K-means算法对高速路流量特征进行聚类,从而划分交通运行状态模式,并将结果与《道路通行能力手册》中的分类结果进行比较。文献[19]以交通流量、时间占有率和平均车速作为聚类指标,利用K-means聚类将交通运行状态分为4种模式。文献[20]选取流量和密度作为聚类指标,分车道进行K-means聚类,同时对比欧氏距离和曼哈顿距离应用于K-means聚类的不同效果,参考《道路通行能力手册》将聚类类别数设置为6类。文献[21]结合行程时间的高斯分布特点,利用GMM算法进行聚类,并对比聚类类别数分别设置为2和3时聚类结果的优劣性。

基于标准规范的分类方法适用性较差,因为不同地区的交通路况和交通基础设施存在差异,对于交通运行状态的评价标准也会有所不同。此外,不同标准规范对于分类指标的要求不一样,部分指标很难做到全路网获取,如流量、密度等。而基于聚类的分类方法大多以单一路段为研究对象,没有考虑路网的整体情况。针对以上不足,本文综合考虑城市路网中多种等级的路段,并参考《城市交通运行状况评价规范 GB/T 33171—2016》[5],以平均行程速度和自由流速度的比值作为聚类指标,结合聚类指标自身的数据分布特点,通过GMM分等级随机抽样聚类算法,提出一种适用于城市路网的交通运行状态模式分类方法。

2 数据描述与清洗

2.1 实验数据

本文研究数据主要包含两部分,即来自国内某导航地图的路段速度数据和路网地图数据。路段速度数据所在区域为佛山市路网,共计40 497条路段的377 375 568条数据记录,数据时间范围为2017年12月1日—2017年12月31日,时间粒度为2 min。路段速度数据的主要字段及其释义如表1所示,其中道路等级字段共包含8种类型,分别为高速路、国道、快速路、主要道路、次要道路、省道、县道和乡公路。

表1 路段速度数据字段释义Table 1 Field interpretation of road speed data

路网地图数据为佛山市路网,共计52 752条路段,并且通过meshiid与road_id字段与路段速度数据相匹配,其主要字段及其释义如表2所示。

表2 路网地图数据字段释义Table 2 Field interpretation of road network map data

2.2 数据清洗

在路网地图数据中,存在无数据路段、无效数据路段以及缺失数据路段,为避免对研究结果造成影响,需要对这些路段进行清除,保留有效数据路段。无数据路段指的是在数据时间跨度内没有数据记录的路段;无效数据路段指的是在数据时间跨度内有数据但数据的速度值多数为0的路段;缺失数据路段指的是在数据时间范围内出现全天没有数据的路段。这3种路段会对本文研究造成影响,因此,需要进行剔除。此外,考虑到县道和乡公路属于低等级道路,很少有车辆行驶,也可能导致数据的可信度降低,因此,也需要剔除这部分路段。最终,实验保留了高速路、国道、快速路、主要道路、次要道路和省道这6种主要城市路段,清洗后路网总路段数为34 039条,其中包含1 935条高速路路段、1 672条国道路段、952条快速路路段、14 737条主要道路路段、8 418条次要道路路段和6 325条省道路段,对应的导航地图路段速度数据总量为317 574 210条。

3 交通运行状态模式分类方法

3.1 高斯混合聚类原理

高斯混合聚类模型利用高斯分布概率模型来进行聚类。假设x为n维样本空间X中的随机向量,若其服从高斯分布,则概率密度函数可以表示为:

(1)

(2)

假设样本生成过程服从高斯混合分布,首先根据先验分布α1,α2,…,αk选择高斯混合成分,αi为选择第i个高斯混合成分的概率;然后根据被选择的高斯混合成分的概率密度函数进行采样,从而生成样本。

若数据集D={x1,x2,…,xm}由上述高斯混合过程生成,则令随机变量zj∈{1,2,…,k}表示生成样本xj的高斯混合成分。显然,zj的先验概率P(zj=i)=αi。根据贝叶斯定理,zj的后验分布为:

(3)

当高斯混合分布pM(x)已知时,高斯混合聚类将把样本集D划分为k个簇C={C1,C2,…,Ck},则每个样本xj的簇标记κj由最大后验概率决定,可以表示为:

(4)

对于模型的求解,关键在于求解参数{(αi,μi,Σi)|1≤i≤k}。根据给定样本集D,可以采用最大化对数似然的方法,计算公式如下:

(5)

为使式(5)最大化,常用的求解方法是利用EM算法进行迭代优化,在迭代过程中不断更新参数αi、μi和Σi。参数更新公式如下:

(6)

(7)

(8)

3.2 分等级随机抽样聚类

城市路网由不同道路等级的路段组成,如高速路、国道、快速路、主要道路、次要道路和省道,而不同道路等级的路段有着不同的限速,这也导致各自的自由流速度有所不同,使得不同等级路段的交通运行状态模式分类标准有所差异。为消除这种差异,同时建立适用于全路网路段的交通运行状态模式分类方法,本文借助归一化的思想,利用路段的自由流速度对路段平均行程速度进行归一化处理,并以此作为聚类指标,在高斯混合聚类的基础上,提出分等级随机抽样聚类的方法。在此基础上,分等级抽取等量的路段进行多次抽样聚类实验,计算前后两次聚类结果的标准化互信息(Standardized Mutual Information,NMI)指标,通过NMI的收敛情况选择路段抽样数。此方法不仅可以大幅提升聚类效率,而且还能涵盖路网各个等级路段的交通运行状态模式。

3.2.1 聚类指标

交通运行状态模式分类的指标有多种选择,如流量、速度、密度等。然而,很多指标的获取依赖于固定的交通检测设备,如流量、密度、占有率等,这也导致这些指标无法用于大规模路网交通运行状态模式分类。而速度的获取则相对灵活简单,在浮动车技术和导航地图软件的普及下,大规模获得路网中路段的实时平均行程速度变得相对容易。因此,基于实验数据,本文采用相对速度作为聚类指标,即路段平均行程速度与自由流速度的比值,这与《城市交通运行状况评价规范 GB/T 33171—2016》[5]中的分类指标是一致的。采用该指标的好处是可以消除因道路等级差异导致的限速差异对聚类的影响,相当于对路段平均行程速度进行归一化处理。相对速度的计算公式如下:

(9)

其中,Ri表示路段i时刻的相对速度,vi表示路段i时刻的速度,vf表示路段的自由流速度。

3.2.2 抽样聚类流程

由于路网数据量过于庞大,如果将其全部纳入聚类将会耗费大量的时间。实际上,许多路段数据的交通运行状态模式是相似的,如果从路网中选取足够的路段样本,使得路段样本的数据足以代表整个路网的交通运行状态分布,就可以在大幅提高聚类时间效率的同时,对路网中存在的交通运行状态模式进行挖掘分类。

基于以上思路,同时考虑到不同等级的路段,本文采用分等级随机抽样的思想,分别从高速路、国道、快速路、主要道路、次要道路和省道中随机抽取n条路段,抽样总数为6n条,以保证抽取的样本能涵盖6种道路等级路段的交通运行状态模式,从而适应不同道路等级路段的分类需求。本文进行多次采样聚类实验,保留每次实验的分类模型以便调用。分等级随机抽样聚类流程如图1所示,目的是选取一个合适的采样路段数,在加快聚类效率的同时,保证选取的样本量足以代表整个路网的交通运行状态模式分布。

图1 分等级随机抽样聚类流程Fig.1 Procedure of hierarchical random sampling clustering

分等级随机抽样聚类步骤如下:

步骤1设置实验次数N,初始化循环次数n=1。

步骤2分别从6类道路等级路段中抽取n条路段,从历史数据集中筛选相应的6n条路段的数据。

步骤3对抽样的路段数据进行高斯混合聚类。

步骤4存储计算完毕的分类模型。

步骤5判断是否达到实验次数,达到则退出循环,否则n递增1,重复步骤2～步骤4。

3.2.3 采样路段数确定流程

采样路段数确定流程如图2所示。通过随机选取1 000条路段的数据作为验证集,对上文中得到的n个聚类模型进行验证,得到对应的n种交通运行状态分类结果,按聚类样本量从小到大的顺序计算前后2种分类结果的NMI指标,得到(n-1)个NMI值。随着聚类样本量的增加,当NMI基本保持不变时,可以认为随着聚类样本量的增加,模式分类结果基本不变。可以将此过程看作是一个近似收敛的过程,说明此时采样路段具有代表性,采样路段的交通运行状态模式分布足以代表整个路网的交通运行状态模式分布。

图2 采样路段数确定流程Fig.2 Procedure of determining the number of sampled roads

采样路段数确定步骤如下:

步骤1随机选取1 000条路段数据形成验证集数据。

步骤2设置实验次数N,初始化循环次数n=1。

步骤3调用第n个分类模型,计算分类结果。

步骤4存储第n个分类模型的分类结果。

步骤5判断是否达到实验次数,达到则退出循环,否则n递增1,重复步骤3和步骤4。

步骤6计算NMI值。

NMI是聚类中常用来衡量两个聚类结果相似度的指标,取值范围为[0,1],越接近1代表两次聚类结果越接近。实验对前后两次聚类的模式分类结果计算NMI值,如果前后两次聚类的NMI非常接近1且基本保持不变,说明采样路段数已达到合适的值。

4 实验与结果分析

4.1 分等级随机抽样聚类结果

实验中聚类的历史数据时间为2017年12月1日—2017年12月24日,将聚类模式数设置为5,关于聚类模式数的选取依据将在下文进行说明。聚类实验循环进行850次,得到对应的850个聚类模型。通过图2流程确定采样路段数,验证集的数据时间为2017年12月25日—2017年12月31日,绘制NMI变化曲线,如图3所示。从中可以看出,当采样路段数大于3 000时,曲线大致收敛在0.95以上,说明此时的交通运行状态模式分类结果的差异较小。因此,确定采样路段数为3 600条,因为即使再增加采样数,不仅对分类结果的影响很小,而且聚类时间也会增加,说明此时的采样数是较为合理的。

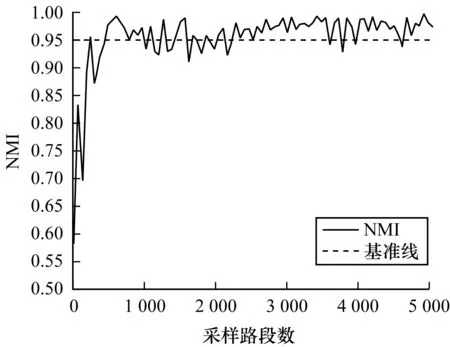
图3 NMI随采样路段数的变化曲线Fig.3 Changing curve of NMI with number of sampled roads

4.2 相对速度分布模式

为探究数据自身的模式分布特点,对相对速度的分布进行分析,计算其分布频率。相对速度是一系列离散值,范围为[0,1],为进行频率统计,将[0,1]划分为100个小区间,区间长度为0.01,统计每个区间内的样本数,采样路段数为3 600条。计算其在2017年12月1日—2017年12月24日期间的相对速度分布频率,并利用高斯分布函数进行拟合,从而得到相对速度的分布频率直方图和密度曲线,如图4所示。从中可以看出,基于相对速度指标可以将交通运行状态模式分为5类,并且每一类均大致服从高斯分布,这也是本文采取GMM聚类模型对数据样本进行模式分类的原因。

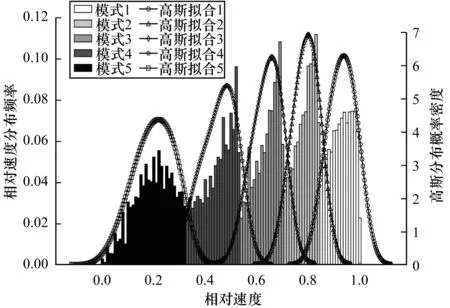
图4 相对速度分布模式Fig.4 Distribution mode of relative speed

4.3 不同聚类模式数比较

现有的研究和相关标准通常将交通运行状态模式分为3类～6类不等,进而分别描述不同程度的畅通和拥堵状态模式。为使得模式数的确定有客观依据,本文比较不同模式数下的聚类结果。实验中将模式数a设为2～9,对于每一组单独进行聚类实验,每一组聚类结果对应的各个模式的聚类中心相对速度如表3所示。从中可以看出,当模式数大于5时,部分模式的聚类中心出现了明显的重叠,即交通运行状态模式无法被明显区分,显然此时的模式数设置过大,数据中的交通运行状态模式数应小于等于5。

表3 不同聚类模式数下的聚类中心相对速度Table 3 Relative speeds of cluster centers underdifferent numbers of clustering mode

由表3可以看出,当模式数大于5时,交通运行状模式已经出现重叠,因此,不考虑模式数大于5的情况。为进一步比较模式数为2～5的聚类结果,本文计算DBI指标。DBI是聚类中常用来评价聚类效果优劣的指标,其值越小,表明类内距离越小,类间距离越大,聚类效果越好。由图5可以看出,随着聚类模式数的增加,DBI逐渐减小,当模式数为5时,DBI最小,表明此时聚类效果最优。因此,本文将聚类模式数确定为5。

图5 DBI指标随聚类模式数的变化曲线Fig.5 Changing curve of DBI index with number ofclustering modes

4.4 不同方法比较

将本文GMM聚类结果与国标(GB/T 33171—2016)、FCM聚类和K-means聚类的结果进行相关性分析,分析相对速度与模式分类标签的相关性,并计算不同方法分类结果的DBI指标,从而对比不同分类方法的优劣性。首先可以确定的是,相对速度与模式分类标签是呈现负相关的,因为实验中模式标签越大,平均相对速度越小。由表4可以看出,GMM聚类的负相关性最强,DBI虽然比FCM和K-means聚类的略大,但是由于聚类样本量是千万级的,因此DBI的差异分摊到每个样本上几乎为0,对结果的影响可忽略。综合对比来看,GMM聚类对于相对速度分布的可解释性更好,而且相关性比其他方法更强。此外,国标分类结果的相关系数表现不佳,说明了国标不能适应各地的交通路况实情。

表4 不同方法的相关系数与DBI指标Table 4 Correlation coefficients and DBI indexes ofdifferent methods

4.5 不同模式下交通运行状态分析

本文对不同模式下的整体交通运行状态进行分析,并且对其时间分布频率进行统计,结果如图6所示。由表3可知:在模式数为5的情况下,模式1～模式5的聚类中心点相对速度逐渐减小,表明交通运行状态在逐渐变差;模式1与模式2的相对速度较大,表明这两类模式的交通运行状态比较接近自由流下的交通运行状态,属于畅通的状态。从图6中也可以看出:这两类模式在时间分布上比较均匀,没有出现明显的峰值;而从模式3开始,相对速度明显变小,特别是模式4和模式5,并且它们在时间分布上呈现出明显的双峰现象,集中在早晚高峰,此时是交通出行高峰期,最大的特点就是会出现交通拥堵,说明这三类模式是属于拥堵状态;模式3是从畅通到出现拥堵的过渡状态,双峰分布初步显现;模式4和模式5的双峰分布则十分显著,并且模式4的拥堵程度高于模式3,模式5的拥堵程度高于模式4。

图6 不同模式的时间分布Fig.6 Temporal distribution of different modes

5 结束语

针对现有城市路段交通运行状态模式分类研究适用性差和研究对象单一等不足,本文提出一种基于高斯混合分等级随机抽样聚类的交通运行状态模式分类方法。以佛山市为例,利用导航地图的路段速度数据,在参考国标分类指标的基础上以相对速度为聚类指标分析相对速度模式分布,发现交通运行状态模式存在类似高斯混合分布的特点,因此采用高斯混合聚类的方法。面对大样本量聚类,进一步提出基于分等级随机抽样的聚类方式以提高聚类时间效率。实验结果表明,GMM聚类具有较好的可解释性,同时能合理划分交通运行状态模式。本文方法结合分等级随机抽样的思想和数据自身特点,通过高斯混合聚类实现了大规模数据下城市路段交通运行状态模式的有效挖掘,具有较好的可解释性和适用性。下一步将在本文研究基础上采用深度学习方法对交通运行状态进行预测,并基于交通运行状态模式分类探究路网交通运行状态的演变趋势。