无源无线应变传感器的模拟与测试

薛松涛 徐康乾 谢丽宇，* 薛 科 万国春

（1.同济大学结构防灾减灾工程系，上海200092；2.日本东北工业大学工学部建筑学科，日本仙台；3.同济大学电子与信息工程学院，上海201804）

0 引 言

在使用荷载以及环境作用下建筑结构的性能会逐渐发生退化，因此结构健康监测在近几十年来得到了广泛的发展，用于监测和评估结构的状态［1］。

在结构健康监测中，应变监测是一个重要的内容，通过监测应变判断结构构件的受力状态，为结构评估提供合理的依据。应变监测中常用的传统应变传感器有电阻应变传感器［2］、光纤光栅传感器［3］和弦振式应变传感器［4］等。这些传统的传感器性能可靠，使用方便，但是需导线为传感器提供电源以及进行数据传输。当大范围布置传感器时，大量的导线使传感系统变得冗杂，并且在灾害发生时容易损坏致使传感系统不能正常工作。

土木工程有其自身的特点，对传感器有着与其他领域的不同要求，需要针对土木工程的特有环境开发出满足需要的传感器［5］。将健康监测系统应用在大规模的土木工程，为了监测局部的物理量，需要大量的传感器，形成具有分布式传感器的监测系统（distributed sensor-based SHM），要求传感器造价低、可靠性好，这样才可以提高传感器空间分布的密度［6］（spatial granularity）。因此，需要寻找一种无须能源供应、可无线传输、耐久性好且价格低廉的传感器，用于结构局部损伤的监测。RFID（Radio Frequency Identification）即射频识别技术可满足这些要求［7-8］，为大规模分布式传感器监测系统的应用提供了可能［9］。

在RFID 系统中，天线起着重要的作用，它是接收和辐射电磁波的装置，必须具有合适的形状、结构和馈电方式。随着进一步的研究，学者们发现天线经历应变时，天线的电学性质（如谐振频率）发生改变，因此天线可同时作为应变传感单元和信息传输单元，实现传感的无源和无线。Yi等［10，11］开发了一种矩形贴片天线传感器用以检测应变，贴片天线频带较窄，谐振频率易于提取。2017年，薛松涛等［12］提出了一种不带芯片的矩形贴片天线应变传感器，天线的工作频段为2.45 GHz，通过数值模拟和试验证实了贴片天线可作为可靠的应变感应单元，具有良好的线性，精度可达万分之一个应变，但其传输方式仍采用了同轴线。本文在该研究的基础上，增加了芯片，重新设计了电路［13］，实现了贴片天线应变传感器的无源和无线。

本文设计了一种工作频率为920 MHz的四分之一矩形贴片天线应变传感器。相比于传统电阻应变传感器，天线传感器的厚度尺寸较大，这导致因剪力滞后效应引起的传递效率将不可忽略。本文将采用数值模拟和试验的方法验证该现象并确定传递效率系数，结合理论推导进而给出传感器灵敏度系数的计算公式。最后设计拉伸试验将传感器灵敏度系数的计算值与实测值相对比，验证天线传感器检测应变性能的可靠性。

1 RFID应变传感系统

RFID 是一种利用射频通信实现的非接触式自动识别技术，按照是否需要外部供电分为有源和无源（Passive）两种。如图1（a）所示，基于RFID技术的无源无线应变传感系统由RFID 阅读器和RFID 天线传感器组成。天线传感器（图1（b））包括贴片天线和IC 芯片两部分。其中，贴片天线为应变感应和信息传输单元，由基板、上辐射贴片、下辐射贴片、过孔和匹配线构成；IC 芯片为回路的负载，可存储位置等信息。

图1 RFID应变传感器系统Fig.1 RFID Strain sensing system

天线传感器与阅读器通过电磁波完成能量的传递以及信息的传输。天线传感器接受电磁波后贴片天线产生电流与负载形成回路，其中在贴片天线中电流的方向即为传感器的长度方向，如图1所示。

该应变传感器是根据贴片天线的谐振频率检测应变。谐振频率是天线的最佳工作频率，即在此频率下RFID 系统的功率传输达到最大化。接下来，第1.1 节将讨论如何进行贴片天线的设计；第1.2节将对天线的谐振频率与应变的关系进行理论推导；第1.3节将介绍试验中谐振频率测量的原理与方法。

1.1 RFID天线设计

对于四分之一波长的矩形贴片天线，其初始谐振频率由下式近似计算［14］：

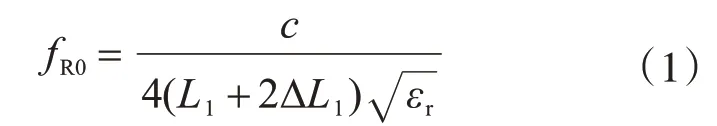
式中：fR0为初始谐振频率；c为真空中光速；L1为上辐射贴片的长度；εr为基板的相对介电常数；ΔL1为考虑介质板效应的补偿介电长度。

依据式（1）对贴片天线进行设计，基板材料选用RT/duroid®5880，相对介电常数为2.2，尺寸选为69 mm×61 mm×0.5 mm，上辐射贴片和下辐射贴片均为镀铜层，上辐射贴片尺寸选为54.9 mm×50 mm×0.1 mm，下辐射贴片尺寸为69 mm×61 mm×0.1 mm，与基板平面尺寸相同。天线具体尺寸见图2与表1，将尺寸参数带入式（1），计算得天线初始谐振频率为918.10 MHz。

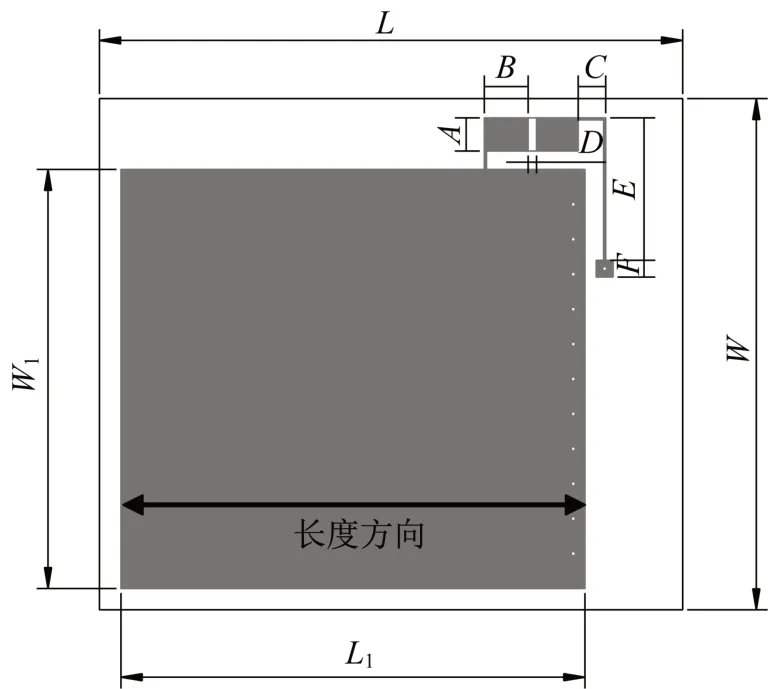
图2 天线尺寸参数Fig.2 Dimensions of antenna

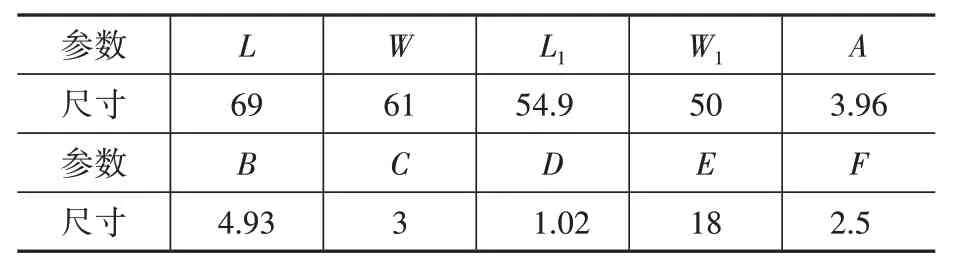
表1 天线具体尺寸Table 1 Antenna specific dimensions mm

1.2 应变测量的原理

根据式（1）可知，天线谐振频率fR受上辐射贴片的长度L1和补偿介电长度ΔL1的影响。一般L1》ΔL1，若忽略ΔL1的影响，当贴片天线在长度方向经历应变ε时，上辐射贴片的长度将变为L1(1+ε)，代入式（1）可得对应的谐振频率fR：

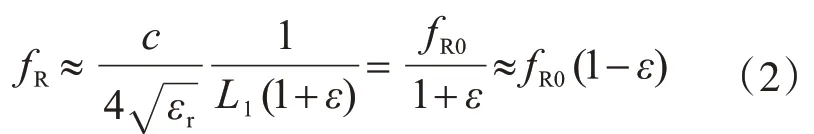
可发现贴片天线的谐振频率fR与其长度方向的应变简化为近似的线性关系，斜率的绝对值为初始谐振频率fR0。也即天线的长度方向为传感器的应变感应方向，而因泊松效应引起宽度方向的变形对谐振频率的影响可忽略。因此，通过测量天线的谐振频率变化可推算出天线长度方向所经历的应变变化。

1.3 天线谐振频率的测量

如图1（a）所示，假定阅读器与天线之间无障碍物，由Friis 自由空间公式可得天线的接收功率P2［15］：

式中：P1为阅读器发射功率；G1为阅读器天线增益；G2为贴片天线增益，λ为阅读器所发射电磁波的波长；d为阅读器与贴片天线之间的距离；f为阅读器所发射电磁波的频率，即天线的工作频率。

天线接收来自于阅读器的功率并向负载传输，其中一部分功率被反射而不能被利用，定义反射系数η(f)为

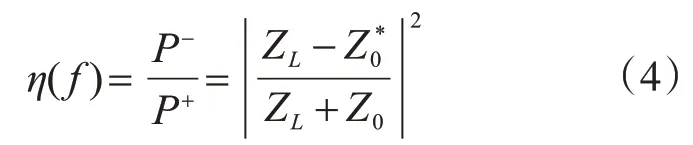
式中：P-为反射功率；P+为输入功率；ZL为负载阻抗；Z0为贴片天线的特性阻抗；Z*0为贴片天线特性阻抗的共轭，其均为天线工作频率的函数。当天线的工作频率等于谐振频率时，天线与芯片的阻抗最佳匹配，η(f)取得最小值，即谐振频率是天线的最佳工作频率。

通过反射系数可得芯片所接收的功率P3为

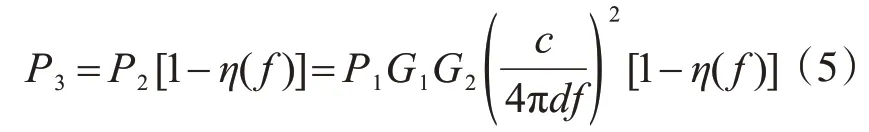
功率由芯片再次返回贴片天线时，同样有一部分功率被反射，反射系数同式（4），所返回的功率P2'为

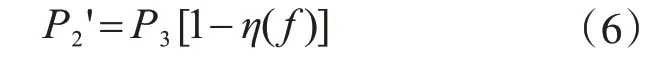
此时贴片天线作为一个功率为P2'的发射源发射电磁波，类比式（3），阅读器天线接收到的功率即反射功率P1'为

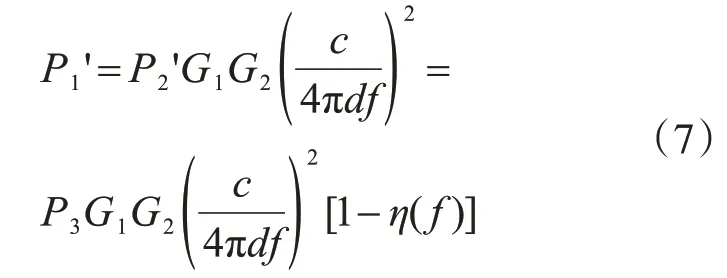
芯片作为一个负载，正常工作所需的最小激活功率为PIC，其不随天线工作频率f改变。在某一频率f下，当芯片恰好被激活时，芯片的接收功率为

将式（8）带入式（5），可得该频率f下的阈值发射功率P1S：

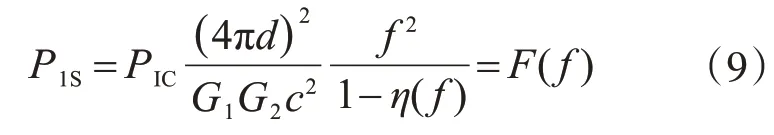
将式（8）带入式（7），对应的阈值反射功率P1S'为

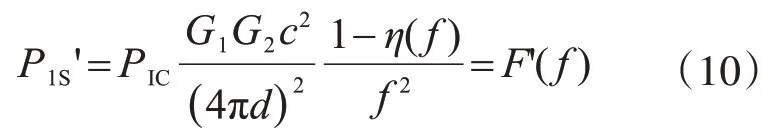
阅读器天线和贴片天线的增益G1和G2均为一常数，其间距固定时d也为定值。当阅读器所发射电磁波的频率f改变时，根据函数η(f)的特性可知，函数F(f)有最小值，函数F'(f)有最大值，即在某一频率范围内阈值发射功率最小值点和阈值反射功率最大值点对应的频率为天线的谐振频率（图3）。因此，可根据采集的阈值发射功率曲线和阈值反射功率曲线确定天线的谐振频率。

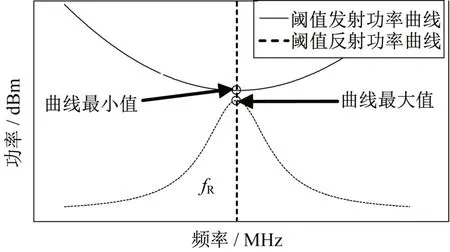
图3 阈值功率曲线示意图Fig.3 Threshold power curves

2 应变传递效率验证

通过强力胶将RFID天线粘贴在试件表面，进行试件的拉伸试验，由于存在剪力滞后效应，天线上辐射贴片的应变不会达到试件表面应变的大小。本节通过数值模拟及拉伸试验对剪力滞后效应进行验证，并根据试验结果计算应变的传递效率系数。试件单向拉伸时的拉伸方向定义为纵向，垂直于拉伸的方向为横向，在复杂应力状态下两个主应变方向分别定义为纵向和横向。则纵向传递效率系数η可按下式计算：

式中：εc为上辐射贴片的纵向应变；εs为试件的纵向应变。

横向传递效率系数η'的定义类比式（11），为上辐射贴片与试件横向应变的比值。但若天线的主要部件基板与试件的泊松比不同，则会引起纵向传递效率系数与横向传递效率系数的差异。

选用铝板作为拉伸试件，由于所用夹具（WDW-50，济南测试厂）的限制，端部尺寸不得超过3 cm，而粘贴天线的区域不得小于天线最大尺寸6.9 cm，故本试验所用试件模型如图4 所示。其中区域I 为加载区域，区域II 为力传递区域，区域III 为传感器粘贴区域。经过传递区域可保证中间传感器粘贴区域所受到的拉应力均匀分布。

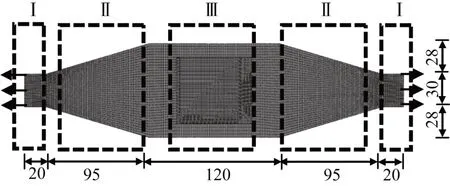
图4 有限元模型（单位：mm）Fig.4 The finite element model（Unit：mm）

2.1 数值模拟

采用ABAQUS 软件建立有限元模型，其中铝板和基板采用实体单元，上、下辐射贴片采用壳单元，各部件厚度及材料参数如表2 所示。模型中不考虑胶水的影响，即假定天线与铝板之间界面的变形是连续的，没有应变的损失。

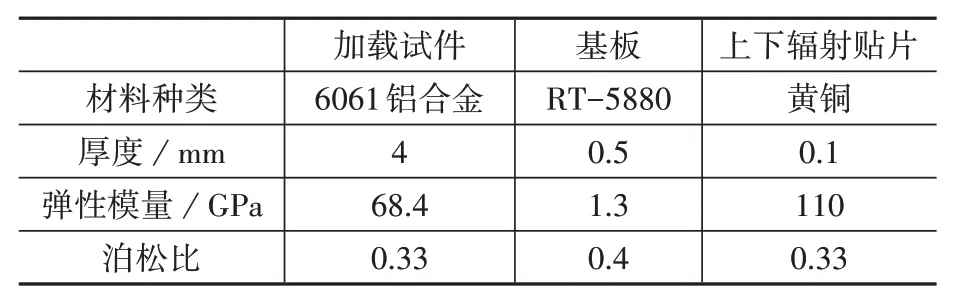
表2 材料参数Table 2 Material parameters

划分网格时，考虑到天线边缘应变变化可能较大，所以网格划分较细密，以保证计算精度；铝板的力传递区域由于拐角的存在会产生应力集中，但不是本文所研究的重点，所以网格划分相对稀疏，以提高计算效率。划分网格之后的ABAQUS有限元模型平面图如图4所示。

在3 kN 荷载作用下，粘贴天线的试件与未粘贴天线试件的纵向应变云图如图5 所示。可见两试件应变云图基本一致，即粘贴天线后对铝板应变的影响可忽略，所以铝板的纵向平均应变可通过公式近似计算得到，此时平均应变为127.5με。

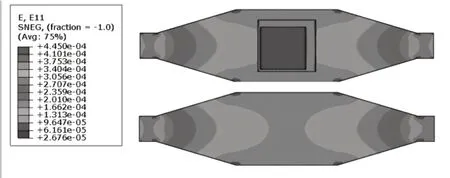
图5 有无天线时的纵向应变云图Fig.5 Strain contour with and without antenna

天线及附近铝板的应变云图与天线上贴片天线的应变云图如图6 所示。在上辐射贴片的边界区域，应变值由铝板的平均应变127.5με快速衰减至 90.6～96.4με之间，如图6（b）所示。提取上辐射贴片的平均应变为94.5με，计算得纵向应变传递效率系数为74.12%。

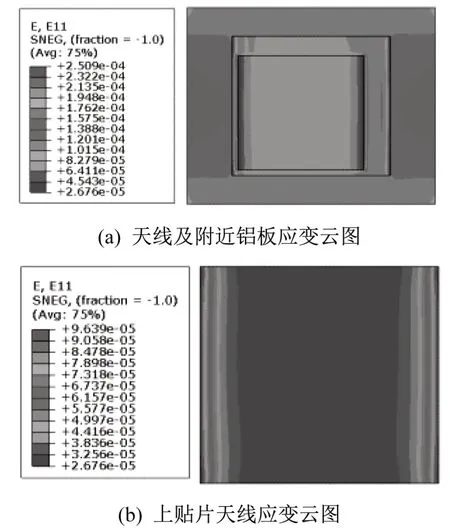
图6 局部应变云图Fig.6 Local strain contour

在此荷载作用下提取铝板横向平均应变为42.2με，与铝板纵向平均应变比值为0.331，接近铝材泊松比；提取上辐射贴片横向平均应变为37.5με，与上辐射贴片纵向平均应变比值为0.397，接近基板泊松比。因此，可知纵向传递效率系数与横向传递效率系数之比约为铝板与天线基板泊松比之比：

式中：vA为铝板泊松比；vS为基板泊松比。

2.2 传递效率试验

通过强力胶将RFID天线粘贴在试件表面，并在上辐射贴片表面和试件表面粘贴应变片，进行试件拉伸试验，验证应变的传递效率。试样如图7（a）所示，应变片①和②粘贴在上辐射贴片表面，应变片③和④粘贴在铝板表面。其中应变片①和③的应变感应方向与拉伸方向平行，应变片②和④的应变感应方向与拉伸方向垂直。拉伸机型号为SJV-30000，拉伸装置如图7（b）所示，应变采集仪选用LC1007。试验采用分级加载，以3kN 为一级，加载至24 kN共八级，总共拉伸3个试样，所得荷载-应变图如图8所示。

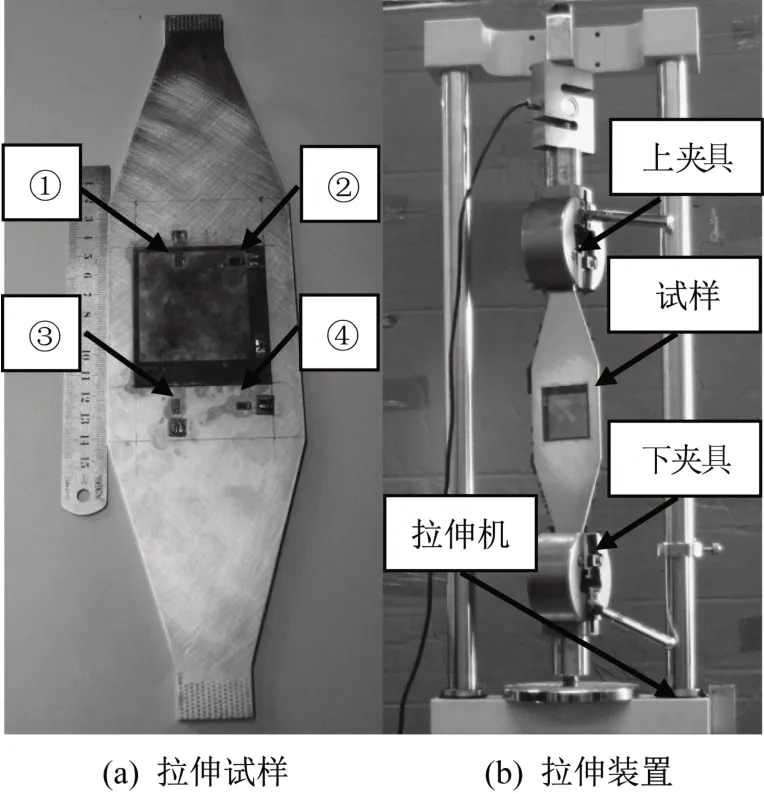
图7 传递效率试验Fig.7 Transfer efficiency experiment

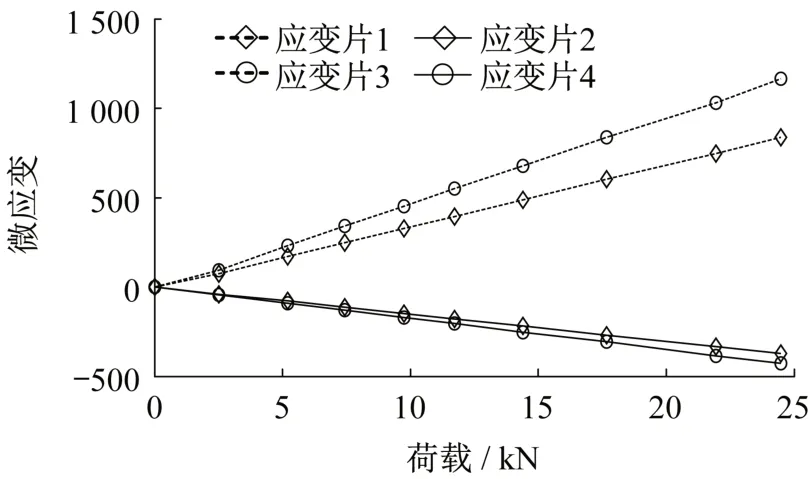
图8 荷载-应变曲线图Fig.8 Load-strain curve

应变片①与③的应变比值为纵向传递效率系数，应变片②与④的应变比值为横向传递效率系数，计算结果如表3 所示。将横向传递效率系数平均值代入式（12）换算为纵向传递效率系数，其值为73.54%，与直接所得的纵向传递效率系数74.23%的相对误差仅为0.93%，非常接近。因此取二者平均值73.88%作为纵向传递效率系数的试验值，与数值模拟所得传纵向递效率系数74.12%的相对误差为0.3%，两者符合较好。

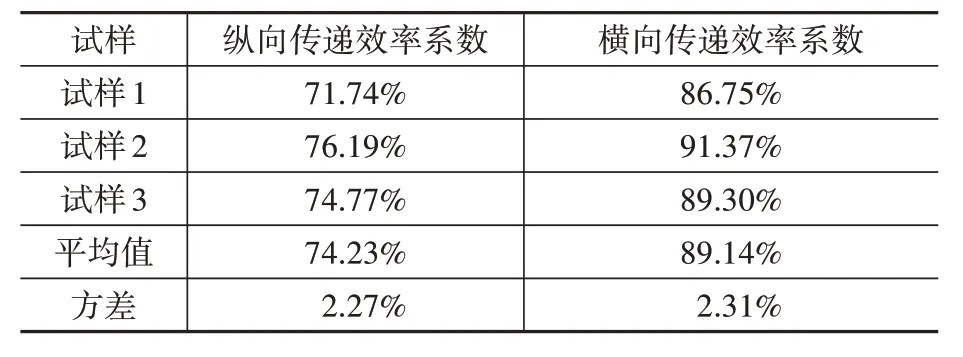
表3 传递效率试验结果Table 3 Experimental results of transfer efficiency

2.3 灵敏度系数

试件在传感器应变感应方向的单位应变所引起天线谐振频率的改变量为天线应变传感器的灵敏度，结合章节1.2推导可得灵敏度系数R：

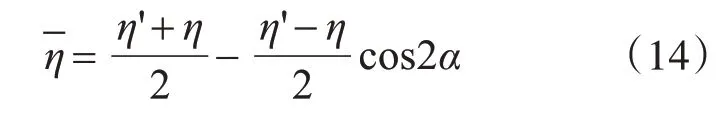
夹角α的取值介于0～90°之间。若为复杂应力状态，则α应为应变感应方向与主应变方向的夹角。

3 天线传感器的测试

当天线传感器的应变与谐振频率有着较好的线性关系时，灵敏度系数的精确性便直接决定了应变检测的准确性。因此，本节采用数值模拟和拉伸试验的方法，探究RFID天线传感器经历应变时谐振频率与应变的线性度以及传感器灵敏度系数的精确度。

其中，数值模拟直接控制天线的应变，此时不需考虑传递效率，所拟合直线的斜率即为传感器的灵敏度系数，根据理论推导直接将其与天线的初始谐振频率进行比较，验证与理论值的符合程度。

设计拉伸试验时，考虑传感器的应变感应方向与拉伸方向平行和垂直的两种情况。试验所得应变-谐振频率拟合直线的斜率即为实测灵敏度系数，将其分别与经式（13）所得计算灵敏度系数相对比，验证传递效率对灵敏度系数的影响。

3.1 数值模拟

在HFSSTM中建立模型，假设天线发生均匀变形，通过改变天线尺寸L、W、L1以及W1等相关参数的方法模拟天线应变［16］，此时不需考虑应变传递效率的影响。由于软件求解精度的限制，若相邻两级的应变增量较小可能会出现较大误差。故在数值模拟中，天线应变以2 000με为一级，加载至10 000με，所得的回波损耗曲线如图9所示，其中回波损耗系数S11定义为

由1.3节中函数η(f)的性质可知，当回波损耗曲线取得最小值时的工作频率为天线的谐振频率。依此提取各级应变下的谐振频率，绘制应变-谐振频率关系曲线，如图10 所示。所得天线初始谐振频率的模拟值为917.88 MHz，与章节1.1 中式（1）的计算值918.10M Hz的相对误差为0.02%，结果十分一致。拟合直线的相关系数为0.999 1，说明天线的谐振频率与应变具有较好的线性关系；拟合直线的斜率为-915.43 MHz·ε-1，表示每单位应变使谐振频率产生915.43 MHz 的漂移量。其绝对值与初始谐振频率模拟值的相对误差为0.27%，符合式（2）的理论推导。在实际测量中当采样频率小于所测应变对应的谐振频率漂移量时，将不会对测试结果造成过大的影响。

3.2 拉伸试验

为减少环境干扰，拉伸试验在微波暗室里进行，试验装置如图11 所示。阅读器固定在三脚架上，与贴片天线之间的距离为0.4 m。

试验中RFID 阅读器选用Tagformance Pro，可检测工作在超高频段天线的阈值发射功率曲线和阈值反射功率曲线，其所采集的功率为对数功率（单位：dBm），与式（9）和式（10）计算所得功率P（单位：W）的换算关系为

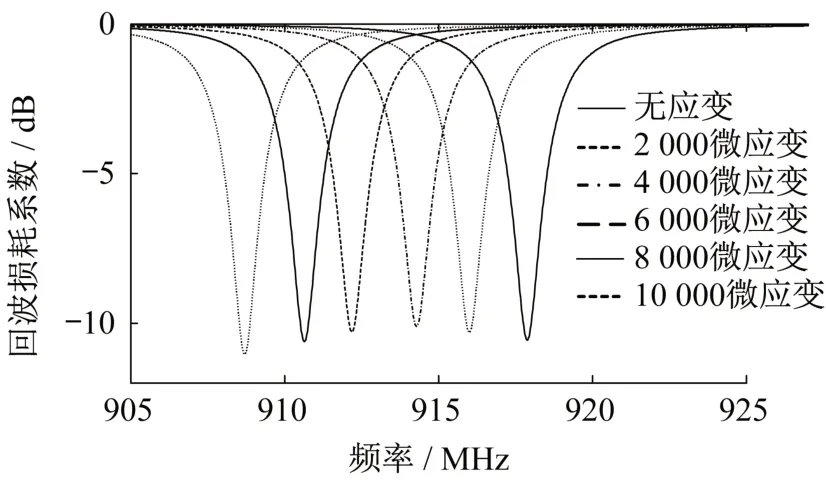
图9 谐振频率偏移曲线Fig.9 Curves of resonant frequency shift

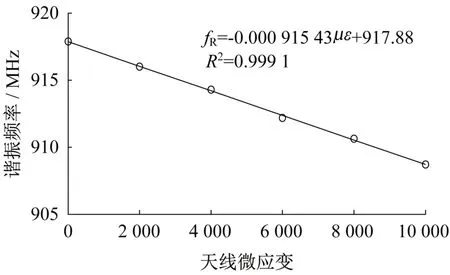
图10 应变-谐振频率拟合直线Fig.10 Fitted line of strain and resonant frequency

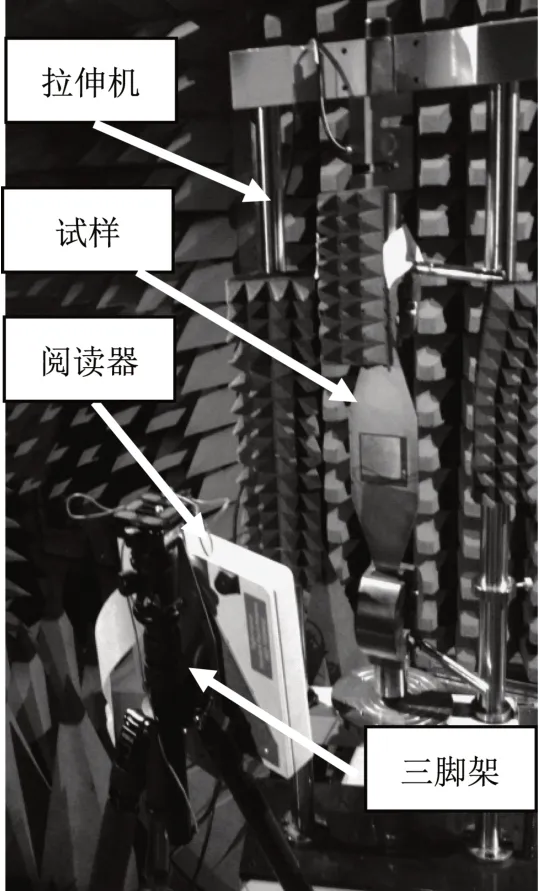
图11 试验装置Fig.11 Experiment setup

试验所用铝板尺寸如图4 所示，采用拉伸机（SJV-30000）对试样分级加载，3 kN为一级共加载8级，与传递效率试验相同。

为探究不同情况下经式（13）所得计算灵敏度系数与实测灵敏度系数的相符程度，将RFID天线传感器粘贴在铝板表面进行拉伸，方案一使天线长度方向与拉伸方向平行，即纵向粘贴，试样如图12（a）所示；方案二使天线长度方向与拉伸方向垂直，即横向粘贴，试样如图12（b）所示。

图12 天线铝板试样Fig.12 Experiment sample

3.3 结果分析

为减小试验误差，每级荷载下分别记录五组数据，其中每组数据包括频率-阈值发射功率曲线和频率-阈值反射功率曲线，分别按式（17）取平均值，所得曲线如图13 所示。可见频率-发射功率曲线波谷相对较平缓，提取最小值时容易引起较大的误差，所以本文中采用频率-反射功率曲线提取谐振频率，以提高精度。

为进一步减小环境噪声的影响，选取频率-反射功率曲线最大值附近的局部曲线，采用四次多项式进行拟合，取局部拟合曲线的最大值点作为天线在该级应变下的谐振频率点，如图14（a）所示。某一试样在无荷载、12 kN 和24 kN 荷载作用下的局部频率-反射功率拟合曲线如图14（b）所示，可见曲线随荷载的增加向着谐振频率减小的方向漂移，与数值模拟的规律一致。提取每级应变下贴片天线的谐振频率，由于加工误差的存在，不同贴片天线初始谐振频率的试验值不相同。为了方便对比，选用谐振频率漂移量作为纵坐标，分别进行应变-谐振频率漂移量的直线拟合，结果如图15所示。

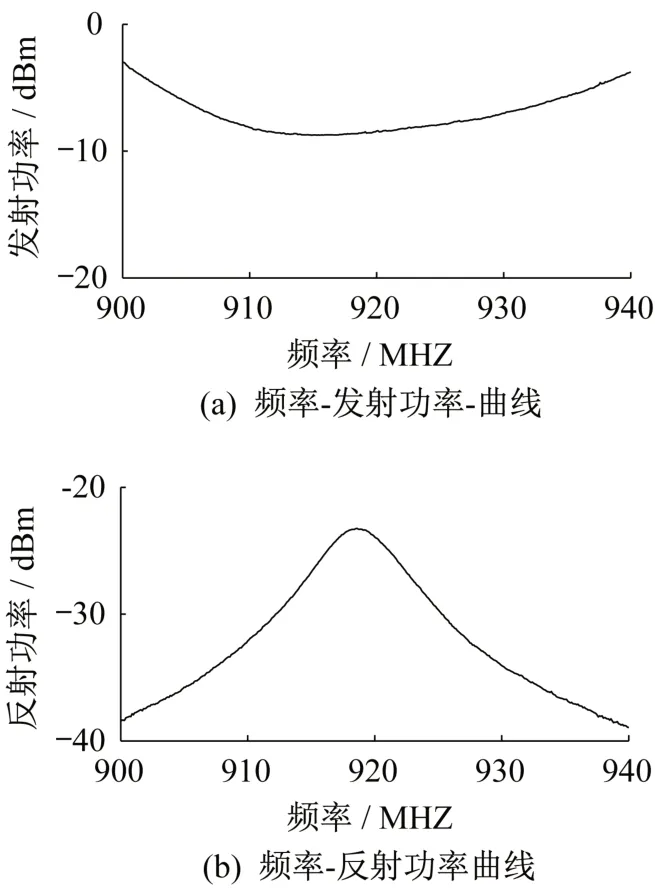
图13 采集数据曲线图Fig.13 Collected data curves

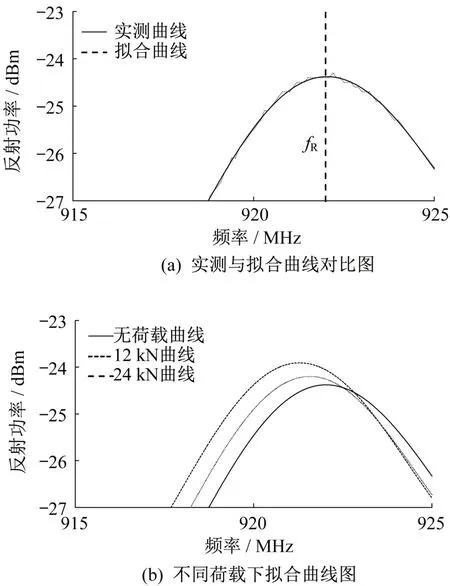
图14 谐振频率的处理及对比Fig.14 The processing and comparison of resonant frequency

对于纵向和横向粘贴的天线，其初始谐振频率与实测灵敏度系数如表4 所示，并根据式（13）得出计算灵敏度系数，其中天线传感器纵向粘贴时传递效率系数取为第2 章节试验结果的平均值73.88%，天线横向粘贴时传递效率系数按式（12）取为73.88×0.4÷0.33=89.55%。

表4 天线初始谐振频率与灵敏度Table 4 The initial resonant frequency and sensitivity

由表4 可见，两组试验所得灵敏度系数的计算值与实测值相对误差的偏差较大，主要是因为采用强力胶粘接天线和试件，而天线的粘接底面积较大，涂胶不均匀会导致局部粘接不牢靠，引起传递效率的偏差。但纵向粘贴和横向粘贴时平均相对误差分别为3.98%和3.52%，均小于5%，满足工程需求。这表明当天线传感器的应变感应方向与拉伸方向平行或存在夹角时均可较准确地检测试件在该方向上的应变。

当天线纵向粘贴时所拟合直线的相关系数接近于1，说明天线谐振频率与应变有着较好的线性关系，与理论推导和数值模拟结论一致。当天线横向粘贴时拟合直线的线性度稍差一些，主要是由于横向粘贴时应变步长以及对应的谐振频率漂移量仅为原先的0.33 倍，在同样的谐振频率测量误差下也会引起拟合直线线性度的降低。因此减小谐振频率的测量误差以提高该传感器的测量精度也较为重要。

4 结 论

本文基于射频识别技术设计了带芯片的贴片天线传感器，实现了应变传感器的无源无线。通过数值模拟和拉伸试验对粘贴在试件上的天线所存在的剪力滞后现象进行了验证，且所得传递效率系数二者相符较好，并依此给出了天线传感器灵敏度系数的计算方法。然后通过模拟和试验对天线进行拉伸，验证了应变与谐振频率的线性关系，且在传感器的感应方向与拉伸方向平行和垂直的两种情况下，实测灵敏度系数与计算灵敏度系数的相对误差均小于5%，试验结果表明该应变传感器可准确检测万分之一量级应变的传感器。

基于贴片天线的特性可知，当天线尺寸不发生变动时其谐振频率的漂移量可以忽略，但当温度改变时会对谐振频率产生影响，下一步将会对温度补偿展开研究。此外，由于该传感器较电阻应变传感器具有较大的尺寸，因此其适用于表面平坦且应力变化较小的结构构件处，未来也将会对此传感器进行小型化的研究。