基于径向基神经网络的Delta机器人位置精度补偿

董慧芬， 高爽笑， 宋金海

(中国民航大学机器人研究所， 天津 300300)

并联机器人的位姿精度是衡量其工作性能好坏的重要指标之一[1-2]。相较之串联机械臂，并联机械臂的多运动链结构能够抵消串联机械臂存在的关节累积效应，因此并联机器人具有高精度的优点。使得并联机器人在分拣、医疗等领域中具有广泛的应用前景。

但是，在实际应用中，由于加工公差、装配误差以及在运动学分析时的一些理想条件达不到、并联机器人运动参数求解的偏差等原因，使得并联机器人的高精度优势难以充分发挥。

为了解决这个问题，通常采用标定和误差补偿的方法来减小Delta并联机器人的运动学参数不精确引起的误差。梅江平等[3]利用激光跟踪仪对并联机器人进行数据测量得到位姿数据，用标定算法进行循环计算，得到机构参数误差，进行误差补偿；任晓栋[4]通过保持动平台上的单轴倾角仪读数分组恒定,构造了一种新型的恒定约束,在此基础上进行了标定。这些标定的方法都在一定程度上提高了机构控制精度，但鲁棒性相对较差，且高精密仪器的成本很高。谢志江等[5-6]提出了一种基于BP(back propagation)神经网络的并联机构正解位移补偿方法，该方法在一定程度上提高了从关节变量空间到工作变量空间的非线性映射精度，虽然对控制器的设计并没有指导意义，但为多耦合映射问题提供了一种快速有效的解决思路。毛冰艳等[7]利用粒子群算法寻优驱动杆参数,修正并联机器人期望轨迹，达到误差补偿的目的。该方法虽然很好地实现了期望轨迹与理想轨迹的偏差补偿，但将并联机器人位姿误差补偿转化为驱动杆参数组合优化问题，导致其普适性不好。陈君杰[8]通过单目视觉对Delta机器人末端位置进行测量，采用误差矢量插值法，实现非实时测量来预测机器人在运行过程中的位置误差情况，达到了不错的效果。但受限于运动速度和系统随机误差，使得该方法鲁棒性不好。彭志文等[9]针对Delta并联机器人动力学问题，提出了一种基于径向基函数(radial basic function,RBF)神经网络的末端计算力矩控制补偿方法，该方法着眼于解决由动力学模型不精确而带来的基于模型控制的精度低问题，为本文研究的运动学问题提供了很好方法借鉴。参看文献[10-11]，RBF神经网络在复杂函数的拟合方面表现优异，在传感器的性能补偿方面也已经取得了显著的成果。

因此，针对Delta并联机器人运动参数求解存在的偏差问题，将RBF神经网络应用于并联机构控制器的设计，结合Delta并联机构运动学逆解，对并联机器人末端位置进行控制，并在Delta并联机器人平台上进行实验验证。

1 Delta机构简化及运动学逆解

1.1 Delta机器人机构简化

如图1所示，Delta并联机器人的机构由静、动平台和3条对称分布的支链组成。各支链中，主动臂与静平台经转动铰连接，从动臂为2条等长的从动杆组成的平行四边形结构，两端分别与主动臂及动平台由球铰连接。3个主动臂在伺服电机驱动下可独立转动，进而使动平台实现三维平动。

图1 Delta机器人模型Fig.1 Delta robot model

可将机构简化，图2所示为Delta机器人的一条支链结构图。

bi为向量与x轴正方向的夹角；θi表示主动臂关节的转角；r表示向量的长度；l1、l2为主、从动臂臂长图2 Delta机器人支链模型简化图Fig.2 Simplified diagram of Delta robot single branched chain

1.2 Delta机器人运动学逆解

并联机构逆解问题表述为：已知并联机构末端移动平台的位置坐标(x、y、z)，求解到达目标位置时，机构三个主动臂关节所需要的转角θ1、θ2、θ3的值。

参看文献[12]，Delta机器人运动学逆解可以表述为

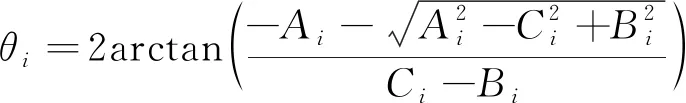
(1)

式(1)中：Ai=2l1(r-ci)Te3，Bi=-2l1(r-ci)T(e1cosβi+e2sinβi)，Ci=(r-ci)T(r-ci)+l12-l22,e1=(1 0 0)T，e2=(0 1 0)T，e3=(0 0 1)T。

2 RBF补偿设计

2.1 控制精度影响因素分析

在Delta机器人运动学逆解的计算中，一般进行诸多理想化的假设，如将关节视为质点、臂杆视为线等，这些假设条件降低了模型复杂度，减小了因模型复杂度引起算法实时性低的影响。但实际应用中很多假设条件无法满足，将导致控制精度降低。另外，运动学逆解求解过程中各种参数测量的不精确，也会引起Delta机器人的实际控制精度下降。

除此之外，加工的公差、装配的误差、工作环境的干扰也是影响控制精度的原因。

通过以上分析可以得出造成控制精度不高的主要原因有以下几点：

(1)逆解模型的理想化，例如，忽略了球铰的大小，将各关节之间的连接看作质点；忽略了电机轴、主从动臂的半径，将其看作线；忽略了电机大小、动静平台厚度，分别将电机和静平台、末端位置和动平台看作在同一平面内。

(2)Delta机器人各参数的测量。如：动静平台外接圆半径测量；主从动臂的长度测量；以及末端位置实际位置的检测。

(3)加工和装配造成的误差。

(4)当前工作环境的干扰。

2.2 RBF神经网络模型设计

RBF神经网络已经被证明能够以任何精度逼近任何非线性函数，并且不存在局部最优的情况。其网络结构简单，具有很强的泛化能力。RBF神经网络的神经元模型如图3所示。

本文要逼近的模型为Delta机器人的实际位置与位置差之间的映射关系模型，该模型有三个输入：实际位置x、y、z和三个输出Δx、Δy、Δz，所以可以得到图4所示的径向基神经网络结构。

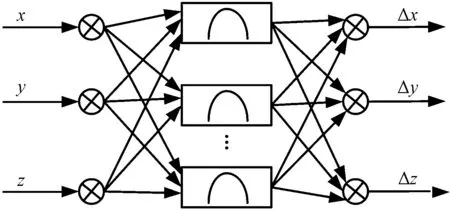
图4 径向基神经网络模型Fig.4 RBF network model

RBF神经网络算法需要求解参数有3个：基函数中心ci、方差σi以及隐含层到输出层的权值ωi。根据径向基函数中心选取方法的不同，RBF神经网络有多种学习方法，如随机选取中心法、自组织选取法、有监督选取中心法和正交最小而成法等。本方法采用自组织选取中心的RBF神经网络学习法。算法流程如图5所示。

图5 RBF神经网络流程图Fig.5 RBF neural network flowchart

(2)

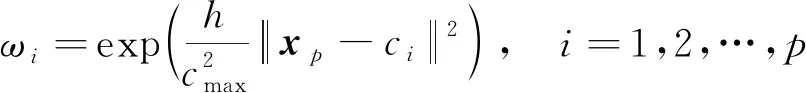
(3)

式中：cmax为所选取中心之间的最大距离；h为隐含层节点总数；p为样本总数；xp为第p个输入样本点；ci为基函数中心。

2.3 基于RBF补偿模型的控制系统设计

由于前述分析的诸多误差产生的原因，当给控制器输入期望的末端位置后，逆解解算出的电机需要的偏转角度与实际的角度存在误差，降低位置控制精度。

为了提高控制精度，将Delta并联机器人运动学逆解与训练后的RBF神经网络结合，来补偿运动学模型的末端位置误差，从而达到精准控制的目的。基于RBF的Delta末端位置补偿控制框图如图6所示，图6中，(x、y、z)p表示期望的位置；Δ(x、y、z)表示期望与实际的位置偏差；RBF神经网络表示输入的位置与位置偏差之间的非线性映射。

图6 基于RBF的Delta末端位置补偿控制Fig.6 Delta end position compensation control based on RBF

控制器部分，如图7所示。图7中：(θ1、θ2、θ3)为电机转动的角度；IK为Delta并联机器人运动学逆解。由图6和图7可知，通过期望位置的输入即可得到能使末端到达该期望位置的运动学逆解输入，再由运动学逆解得到各电机应转动的角度，从而驱动Delta机器人末端到达期望位置。

图7 控制器设计Fig.7 Controller design

3 样本采集、训练及实验验证

为了验证上述提出算法的正确性并描述Delta机器人的可达工作空间，在实验室搭建的Delta机器人平台进行试验，机器人结构具体参数如表1所示。

表1 Delta机器人的参数

3.1 工作空间求解

根据现场工作情况将Delta机器人主动臂输入角度限制在0°～80°。运用搜索算法[13]进行逐点搜索，并将符合条件的坐标点进行存储。使用MATLAB软件生成可视化的工作空间如图8所示。

图8 Delta机器人工作空间Fig.8 Workspace of Delta robot

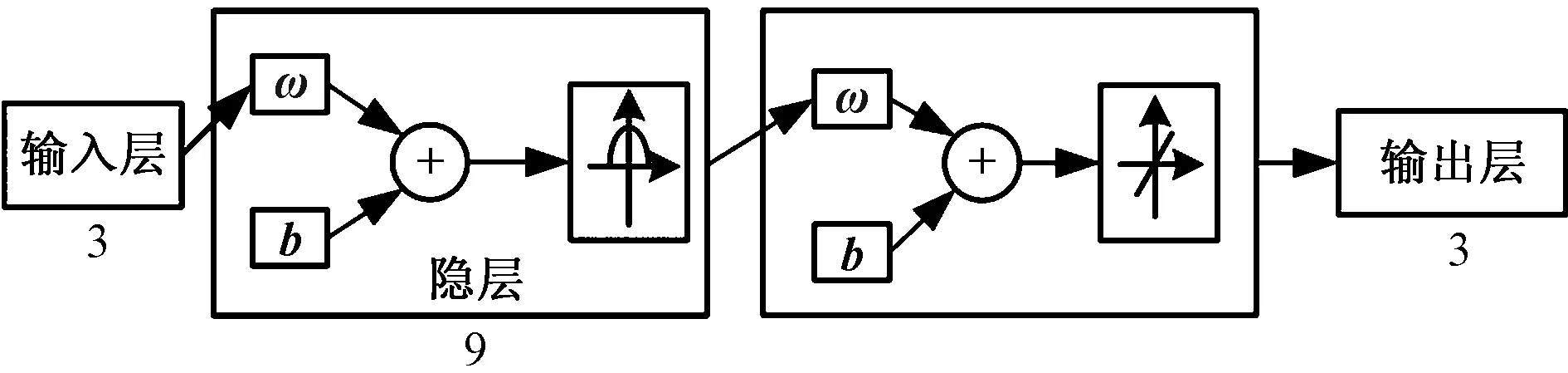
图9 训练后RBF神经网络结构图Fig.9 Structure diagram of trained RBF neural network

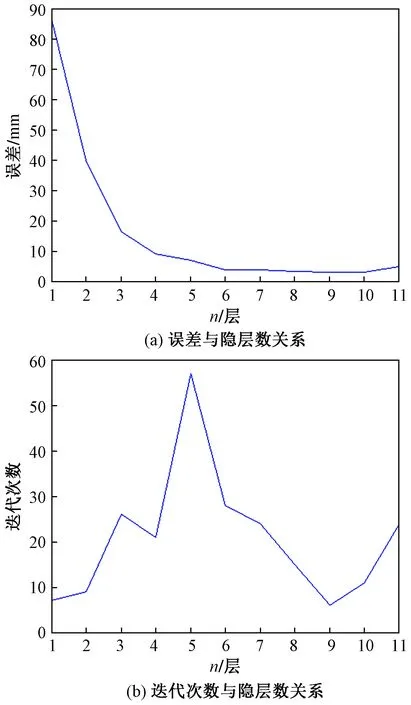
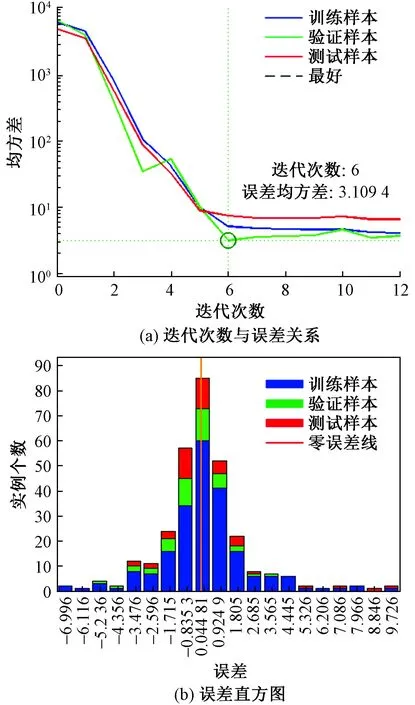
由图8的MATLAB仿真图可知，工作空间全部集中在U={-400

3.2 RBF神经网络样本采集和训练

在当前的输入输出条件限制下，考虑到并联机器人实际项目需求，对末端的位置精度在低点要求较高，因此运动学误差补偿神经网络的训练样本选为：W={-200

按照第3节流程图中给出的算法步骤，可得如图9所示的RBF神经网络。ω和b分别为隐层(hidden)和输出层(output)权值ω和偏置项。

经多次测试，得到图10，隐层层数n与迭代误差和迭代次数的关系图。综合考虑误差大小和迭代速度，选择隐含层基函数个数，可得n=9时最优，此时神经经网络训练图和误差直方图如图11所示。

图10 隐层层数选择依据图Fig.10 The basis of selection of hidden layers

图11 隐层为9时的结果图Fig.11 Results when the hidden layer is 9

由图11(a)可知，当隐层为9时，迭代次数达到6次后，验证集误差上升，证明训练可以结束，整个数据集的误差均方差为3.109 4 mm。由图11(b)可知样本在零误差线周围聚集程度越高，表示神经网络预测效果越好。

此时RBF神经网络的隐层和输出层权值ω和偏置项b矩阵如下。

加载训练好的RBF模型，将测试样本输入，绘制训练前后位置误差对比，如图12所示。

图12 RBF网络测试结果对比Fig.12 Comparison of RBF neural network test result

将实际的位置误差与RBF神经网络输出(补偿的位置误差)做差，即：Δ(x、y、z)-ΔRBF (x、y、z)可得如图13所示结果。

由图12、图13可知，用样本训练而得的神经网络，在测试样本的测试下误差为±3 mm，该RBF神经网络能较好地反映输入输出样本之间的映射关系。

图13 RBF网络训练样本误差分析图Fig.13 Error analysis diagram of RBF neural network training samples

4 Delta平台实验验证

为了进一步验证该方法的可行性，在Visual Studio2017环境下将该神经网络结果进行编译，并使用图8所示的逆解加RBF补偿的控制策略代替Delta逆解控制策略，规划如图8所示轨迹，按照《工业机器人标准测试大纲》中关于机器人实验的重复性及可靠性要求进行实验，以保证验证结果的可靠性，结果如图14所示。

图14 验证实验的结果Fig.14 Verify the results of the experiment

从图14可以看出，使用RBF神经网络训练结果作为控制器的方法使得控制误差由±30 mm 减小到±5 mm。由于实验过程中随机误差的存在，以及实验取值为多次测试的平均值的原因，使得真实的实验结果与RBF仿真模型存在一定偏差。但从实验结果分析表明，该补偿方法在实现精准控制上起到了很好的效果，在一定程度上解决了由于加工公差、装配误差、建模不精确等原因引起的控制精度不高的问题，在控制器设计方面，该控制策略仅仅是将RBF训练后的结果进行离线编译，对原有的基于运动学逆解的控制器进行补偿，所以在稳定性和实时性方面也能得到保障。

5 结论

针对Delta并联型机器人控制精度问题，设计并实现了基于RBF神经网络的精度补偿控制策略。

(1)结合装配、加工以及运动学分析分析了Delta机器人末端位置误差来源，并在此基础上分析了以往的提高控制精度的方法及优缺点。

(2)提出了一种基于RBF神经网络补偿的Delta机器人控制方法。训练后的RBF神经网络验证集样本验证结果表明补偿误差为±3 mm。

(3)将训练后的神经网络应用于Delta并联机构控制器设计，实验结果表明Delta机器人末端位置误差由±30 mm减小到±5 mm，有效地减少了由加工、装配、测量以及模型简化而引起的控制误差。为Delta并联机构的精准控制提供了一种简单易行的方法。