串列不等直径双圆柱海流能发电振子涡激振动数值模拟

2020-12-16白旭，陈云

可再生能源 2020年12期

白旭，陈云

（江苏科技大学船舶与海洋工程学院，江苏镇江 212003）

0 引言

涡激振动是一种常见的流固耦合现象，即流体经过圆柱体时会产生周期性脉动力，进而引发柱体振动，当圆柱体的自振频率与旋涡脱落频率相近时，两者会发生共振，从而产生较大振幅。研究表明，利用圆柱体涡激振动产生的振幅进行发电，能够减少不可再生能源消耗量，具有重要的现实意义[1]。

涡激振动的研究多采用数值模拟和试验分析的方法，在试验分析中，雷诺数Re≥104，在数值模拟中，雷诺数Re≤102。有研究表明，涡脱落过程产生的大尺寸尾流在一定程度上呈高、低雷诺数（102量级）相似的特征[2]。高雷诺数的主要现象和特征可以从低雷诺数问题的研究中得到。在涡激振动发电装置的研究方面，美国密歇根大学发明的VIVACE （Vortex Induced Vibration for Aquatic Clean Energy）能量转换装置的发电原理是将圆柱涡激振动产生的位移通过变速装置带动发电机产生电能[3]。研究表明，在获取能量方面，多柱体较单柱体有较大优势[4]。针对涡激振动多柱体的研究主要从双圆柱入手，进而揭示多柱体的振动规律。

目前，针对双圆柱涡激振动的研究主要集中在等直径串列、并列双圆柱旋涡脱落形式、振动特性等方面。对于直径不等的多圆柱绕流及涡激振动现象的研究相对较少。 Wang H[5]对上、下游圆柱直径比为2 的串列圆柱体进行了数值模拟（50≤Re≤200），其中上游圆柱静止，下游圆柱做垂直流向的单自由度运动或同时做顺流向、垂直流向的双自由度运动，研究结果表明，下游圆柱做垂直流向的单自由度运动时产生的振幅比单圆柱振动和两个等直径圆柱体同条件振动产生的振幅均要大。 Lam K M[6]对并列布置、串列布置和交错布置方式下的上、下游圆柱直径比为2 的双圆柱进行了试验研究，其中上游大圆柱固定，下游小圆柱弹性支撑，研究结果表明，在串列及并列布置方式下，弹性支撑的下游小圆柱的流体诱发振动会受到抑制，而在交错布置方式下，流体诱发振动会被放大。Wang Y T[7]对串列不等直径双圆柱进行了数值模拟（100≤Re≤150），模拟结果表明，直径比（d/D）和间距比（G/D）对升、阻力系数、圆柱周围的压力分布和涡旋脱落频率均有重要影响。

综上可知，针对不等直径圆柱体涡激振动的研究主要集中于双圆柱静止绕流或上游圆柱静止，下游圆柱做单自由度运动的情况，而有关不等直径双圆柱均弹性支撑同时做单自由度运动的研究较少。因此，本文计算分析了上、下游圆柱弹性支撑同时沿垂直流向做单自由度振动的情况，旨在观察该工况下间距比和直径比对双圆柱体涡激振动响应特性及尾涡特征的影响，从而为海流能发电振子系统的直径选取及布置提供理论依据。

1 计算模型

本文计算条件为雷诺数Re=300，位于亚临界雷诺数区间，该范围内的尾涡以固定频率周期进行脱落，便于观察分析。涉及的计算参数：来流速度U=0.14 m/s，空气密度ρ=1.225 kg/m3，流体的动力黏度系数υ 为1.48×10-5m2/s，上、下游圆柱的间距为G，间距比G/D=2～6，上、下游圆柱的质量之比均为2.4，阻尼比ζ=0.001，上游圆柱的直径D=0.032 m，下游圆柱的直径d=0.2D～0.8D。

图1 为计算域及边界示意图。圆柱圆心距离进口边界为15D，距离上、下边界均为15D。进口采用速度入口，出口采用压力出口，上、下边界采用对称边界，圆柱为壁面边界。限定上、下游圆柱均做垂直流向单自由度振动。

2 数值计算方法

2.1 控制方程

不可压缩粘性牛顿流体的控制方程为Navier-Stokes 方程。笛卡尔坐标系中连续性方程和动量方程分别为

式中：u=（Ui，υ）T为流体的速度矢量；Ui为某时刻的速度分量，m/s；P 为压力，Pa。

柱体振动方程可以表示为

2.2 重叠网格技术

在重叠网格方法中，可以使用两种类型的网格（可以针对不同区域独立生成）来离散流场。第一种类型的网格是主要网格（背景网格），它是一个全局笛卡尔网格（整个计算域的H 型网格），该网格固定在空间中。第二种类型的网格是与主要网格重叠，并可以静止或移动的次要网格。对于每个网格分别求解控制方程，并且使用插值算法在主网格和次网格之间有效地传输和交换数据[8]。

在本文中，次要网格（O 型网格）覆盖了圆柱周围的区域。网格之间的数据转换是通过被称为边缘点的特定点来完成的。主要网格（背景网格）的边缘点是放置在圆柱体外部和其表面附近的节点，而次要网格的边缘点是放置在每个次要网格外部边界线上的节点。另一组点称为孔点，在网格中切割并与固体表面相交。为了将信息从网格中的边缘点传输到其他网格中的节点，本文采用搜索算法指定对象网格中该边缘点的周围节点[9]，[10]。

图2 离散化的计算网格Fig.2 Discretized computational grid

2.3 可靠性验证

为了验证本文模型的可靠性，将利用本文模型计算得到的单圆柱及串列双圆柱静止绕流的结果与文献结果进行对比。

2.3.1 单圆柱验证

为了验证程序的正确性，对Re=200 情况下的单圆柱匀速绕流进行了数值模拟。计算得到的升力系数Cl和斯托罗哈尔数St 如表1 所示。由表1 可以看出，本文的计算结果与前人的计算结果吻合较好，验证了程序的正确性。

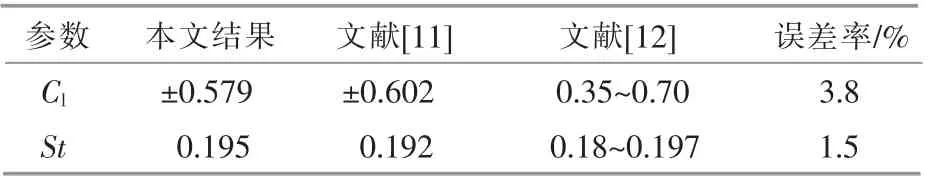
表1 单圆柱绕流结果对比Table 1 Comparison of single cylinder flow results

2.3.2 等直径串列双圆柱验证

为进一步验证计算程序的可靠性，本文对串列等直径双圆柱绕流进行了数值模拟（G/D 分别为1.5，2，3 和4）。计算得到的阻力系数Cd1、阻力系数Cd2和斯托罗哈尔数St 如表2 所示。由表2可以看出，本文的计算结果与前人的计算结果非常接近。因此，验证了本文网格划分、时间步长设置和数值求解格式等程序的有效性和准确性。

表2 双圆柱绕流结果对比Table 2 Comparison of the results of flow around a double cylinders

3 结果与分析

3.1 振幅响应

选取每个周期内振幅的均方根（Yrms）作为振幅幅值，利用振幅比A*=Yrms/D 来分析振幅响应。在不同间距比下，上、下游圆柱的振幅响应随直径比的变化曲线如图3 所示。

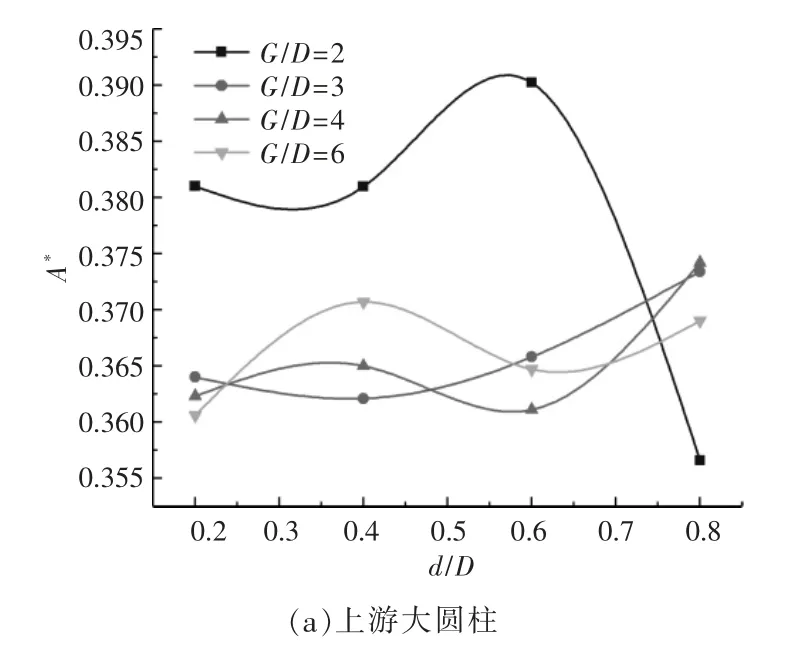
图3 不等直径比下振幅响应示意图Fig.3 Schematic diagram of amplitude response under unequal diameter ratio

从图3 可以看出：上游大圆柱和下游小圆柱的振幅比最大值均在G/D=2 时取得，其中上游大圆柱在G/D=2，d/D=0.6 时取得振幅比A*的最大值（约为0.39D）；下游小圆柱在G/D=2，d/D=0.2 时取得振幅比A*的最大值（约为3.2 d）。在小间距比下，圆柱间的干涉作用较强，上游圆柱的自由剪切层包围整个下游圆柱，增强了下游小圆柱的振幅响应；当d/D 大于0.6，G/D=2 时，随着直径比的逐渐增大，上游大圆柱的振幅比A*逐渐减小；在其他间距比下，上游大圆柱的振幅比A*均随着直径比（d/D＞0.6）的增大而缓慢增加；随着直径比的逐渐增大，下游小圆柱的涡激振动阻力逐渐增大，不同间距比下的振幅比A*均逐渐减小。在串列不等直径双圆柱系统中，在小间距比下，直径比的变化对系统振幅响应的影响较大。

3.2 受力特性

3.2.1 升力特性

在不同间距比下，上、下游圆柱的升力系数均方根Clrms 随直径比的变化曲线如图4 所示。

图4 不同直径比下升力系数均方根的变化曲线Fig.4 Root mean square variation curves of lift coefficient under unequal diameter ratio

从图4（a）可以看出：对于上游大圆柱，当G/D=2，直径比较小时，Clrms 较小，随着直径比的逐渐增加，Clrms 变化明显，并在d/D=0.6 后出现陡增趋势，说明耦合不等直径的双圆柱振动时，圆柱间有较高流速的射流，随着直径比的逐渐增加，下游圆柱对上游圆柱的影响逐渐增强；当G/D=3，4，6 时，随着直径比的增加，Clrms 变化缓慢，且Clrms 随着G/D 的增大而增大；当G/D=6 时，Clrms 的变化趋近于单圆柱的振动情况。从图4（b）可以看出：对于下游小圆柱，当d/D＜0.35 时，Clrms 在G/D=3 时取得最大值；当d/D＞0.35 时，G/D=4 下的Clrms 始终大于其他间距比下的Clrms；随着直径比的逐渐增大，下游小圆柱承受的来自上游圆柱形成的脱落涡的冲击力逐渐增大，上游大圆柱对下游小圆柱的干扰作用逐渐增强，下游小圆柱的Clrms 逐渐增大。在不同间距比（G/D=2 除外）下，下游小圆柱的Clrms 明显高于上游大圆柱的Clrms。

3.2.2 阻力特性

在不同间距比下，上、下游圆柱的阻力系数均方根Cdrms 随直径比的变化曲线如图5 所示。

图5 不同直径比下阻力系数均方根的变化曲线Fig.5 Root mean square variation curve of resistance coefficient under unequal diameter ratio

从图5（a）可以看出：对于上游大圆柱，当G/D 一定时，随着直径比的逐渐增大，Cdrms 出现较强的波动性，这说明当间距比一定时，下游小圆柱的直径变化对上游大圆柱的影响较大；当G/D=3，4，6 时，随着直径比的逐渐增大，Cdrms 的变化趋势相似，但与G/D=2 时的变化趋势相反；当直径比较小时，上游圆柱的自由剪切层重附在下游小圆柱上，下游圆柱处在上游圆柱的尾涡范围内，对上游圆柱的影响不明显。从图5（b）可以看出：对于下游小圆柱，在不同的间距比下，Cdrms 均随着直径比的增大而呈现出增大趋势；当直径比较小时，下游圆柱处于上游圆柱的绕流回流区段，受到与原水流方向相反的作用力，使得Cdrms 较小；随着直径比的逐渐增大，圆柱间的干扰作用减小，下游小圆柱的振动状态逐渐趋近于单圆柱振动状态，使得Cdrms 逐渐增大。

3.3 频域特征

工程中一般用斯特罗哈尔数（Strouhal，St）来确定旋涡脱落的频率。 St 的计算式为

式中：fS为旋涡脱落的频率，Hz。

计算串列不等直径双圆柱绕流时发现，大小圆柱的涡脱落频率相同，但均比单圆柱绕流小。图6 给出了d/D=0.6 时不同间距比对应的升力信号的功率谱密度。

图6 升力的功率谱密度分布示意图Fig.6 Schematic diagram of power spectral density distribution of lift

从图6 中可以看出：当G/D=2，3，4，6 时，上游大圆柱对应的旋涡脱落频率分别为0.908 7，0.931 4，0.933 2，0.934 9，将其带入式（7），计算得到St 分别为0.207 7，0.212 9，0.213 3，0.213 7；随着间距比的增大，旋涡脱落频率逐渐增大，同时St也有略微增大的趋势，但St 总体保持在0.21 左右，这说明St 有一定的鲁棒性且尾流中旋涡泄放规则有序。本文的仿真结果与文献[15]，[16]中的仿真结果相接近，证明了本文仿真结果的有效性。

3.4 尾流特征

当G/D=2 时，不同直径比下的串列双圆柱的瞬时涡量如图7 所示。

从图7 中可以看出：当间距比相同时，随着直径比的增大，尾流形态不断发生改变。当d/D=0.2时，大圆柱分离的剪切层附着于下游小圆柱表面，大、小圆柱后的涡脱落形态较为稳定，呈现双旋涡脱落形态，尾流双旋涡呈现近似平行状态，旋涡脱落不明显，呈现相互连接的状态；当d/D=0.4 时，大圆柱分离的剪切层附着于下游小圆柱上表面，剪切层接触小圆柱表面部分减少，大、小圆柱后均出现稳定的涡脱落现象，旋涡脱落明显；当d/D=0.6 时，大圆柱分离的剪切层不再附着于下游小圆柱下表面，大、小圆柱后均出现稳定的涡脱落现象，旋涡脱落明显，稳定单旋涡数量增加；当d/D=0.8 时，大圆柱分离的剪切层不再附着于下游小圆柱表面，大、小圆柱后均出现稳定的涡脱落现象，旋涡脱落明显，尾流涡之间的连接明显减少，圆柱之间的干涉效应逐渐消失，基本呈现单涡形态。