基于改进云分段模型的光伏功率缺失数据补齐研究
2020-12-16张弘鹏刘家庆段志伟徐志英
张弘鹏, 刘家庆, 段志伟, 徐志英, 方 渊
(1.国家电网公司东北分部, 辽宁 沈阳 110180; 2.国电南瑞科技股份有限公司, 江苏 南京 211106)
0 引言
随着光伏发电在电网中的占比逐渐增大,该技术越来越受到人们的重视。 完整、可信的光伏功率数据成为开展光伏功率预测、电网优化控制和发电性能评估等研究的基础[1]~[4]。在光伏电站实际运行的过程中,由于光伏发电设备和通信会发生偶然性故障,导致光伏功率数据出现大量异常和缺失的问题,极大地影响了研究人员挖掘光伏功率数据所蕴含的信息,因此,补齐光伏功率缺失数据不仅保证了光伏功率数据的完整性,也为光伏发电的研究奠定基础。
导致光伏功率数据缺失的原因包括采集过程中的光伏功率数据缺失、处理异常数据后的光伏功率数据缺失[5],[6]。 目前,光伏功率缺失数据补齐的研究方法可分为3 类:第1 类方法为通过光伏功率数据本身的时序性补齐缺失数据,主要有均值法和相似片段法等,该类方法所用的模型比较简单,且易于实现,但由于该类方法未考虑光伏功率缺失数据的影响因素,过于依赖光伏功率数据本身的连续性,因此,高比例缺失数据和连续缺失数据的数据补齐效果较差[7],[8];第2 类方法为机器学习法,文献[9]利用相关向量机回归模型,基于互信息理论和最大相关、最小冗余原则,通过机器学习挖掘光伏功率与其他各影响因素之间的关系, 并利用上述关系对风电功率缺失数据进行补齐,该方法能够在保持有效信息的基础上,对高维数据进行降维,利用机器学习法时,须要对较多数据样本进行训练,由于计算的复杂度较高,因此, 需要较长的时间才能够补齐缺失的大量光伏功率数据; 第3 类方法为通过构建光伏功率的条件概率分布模型实现光伏功率缺失数据的补齐,文献[10]利用Copula 理论建立风电输出功率的条件概率模型, 基于风机输出功率的相关特性实现缺失数据的补齐,分析结果表明,该方法的补齐效果优于多项式补齐法、持续法和平均值法。通过构建光伏功率的条件概率模型实现缺失数据的补齐,既考虑了缺失数据的相关影响因素,又能够降低运算的复杂度。
由于光伏发电本身具有周期性、 波动性和随机性等特点,因此,上述关于风电功率缺失数据和其他邻域的补齐方法, 对光伏功率缺失数据的补齐效果有待考证。目前,国内对于光伏功率缺失数据补齐方法的研究尚处于起步阶段, 而国外已有一些关于光伏功率缺失数据补齐方法相关研究的资料。 文献[11]通过K-means 聚类算法,以相似的、 含有完整数据的历史日期替代含有缺失数据的日期,该方法在一定范围内是可行的,且可以用于不同类型的时间序列,但该方法过于依赖历史数据的完整性和准确性。 文献[12]首先建立了神经网络方法;然后,运用该方法推测出太阳辐照度缺失数据;最后,通过太阳辐照度-光伏功率模型计算出对应的光伏功率数据。 该方法适用于太阳辐照度和对应光伏功率数据均缺失的情况,但利用神经网络方法和太阳辐照度-光伏功率模型会不可避免地造成二次误差。 文献[13]通过插值方法对太阳辐照度进行缺失数据补齐,再通过神经网络方法训练生成的太阳辐照度-光伏功率模型,对光伏功率缺失数据进行补齐,该方法同样会造成二次误差。
本文对某光伏电站2018 年的光伏功率进行描述和预处理;然后,根据光伏功率输出模型对光伏功率数据进行分段,并利用正向云算法建立传统云模型;接着,利用联合经验函数拟合出太阳辐照度和光伏功率的联合概率密度分布,从而得到各云分段的光伏功率条件概率拟合值,并结合云理论构建改进云模型,根据光伏功率缺失数据的波动性以及云模型的改进结果构建光伏功率缺失数据补齐模型;最后,利用不同方法对不同种类、不同数据缺失比例的光伏功率缺失数据进行补齐,并以准确率和平均相对误差作为指标对各个数据补齐方法进行评价。 本文旨在探索一种更加适合光伏功率数据特征的缺失数据补齐方法。
1 光伏功率数据描述及预处理
本文采用吉林省吉林市高台子区某光伏电站的光伏功率数据进行分析,该电站装机容量为20 MW,光伏功率数据采集时间间隔为5 min。 2018年,高台子地区某光伏电站输出功率的时序图如图1 所示。
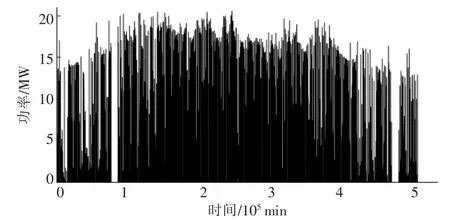
图1 2018 年,高台子地区某光伏电站输出功率的时序图Fig.1 Timing diagram of the output power of a photovoltaic power station in the Gaotaizi area in 2018
由图1 可知,在光伏功率数据采集的过程中,存在某些光伏功率数据缺失的情况。其中,两个较长的连续光伏功率数据缺失时段为1 月19 日6:10-1 月24 日22:30 和10 月20 日4:00 -10月26 日3:45。 此外,还存在某些随机光伏功率数据缺失的时段,该组数据的缺失比例为4.67%。为达到国家电网公司发布的《光伏发电功率预测系统功能规范》 中关于实验数据量的完整性须达到99%以上的要求[14],同时为了构建准确的光伏功率条件概率分布模型, 本文将剔除光伏功率缺失数据、光伏功率超过20 MW 的数据和无太阳辐照度,但仍有光伏功率输出的数据,处理结果如图2所示。
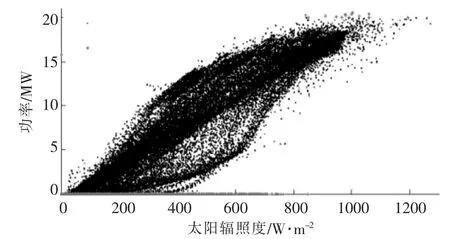
图2 2018 年,高台子地区某光伏电站发电功率数据预处理图Fig.2 Preprocessing of photovoltaic power data of a photovoltaic power station in Gaotaizi district, 2018
由图2 可知, 光伏功率大致会随着太阳辐照度的升高而增加,但由于电池板温度、空气湿度、风速和光照入射角的影响, 某太阳辐照度下的光伏功率数据会分布得比较分散。
2 传统云分段模型及实现
云模型由中国工程院院士李德毅于1995 年提出并应用于智能控制、 数据处理和数据挖掘等诸多领域。正向云算法通过正向云发生器实现,令太阳辐照度为x,通过云模型得到的光伏功率(功率云滴)为gi,i=1,2,…,n。 云模型算法的计算步骤如下。
①以拟合的绝对残差作为指标, 对光伏功率数据样本进行拟合,若拟合的函数为Gaussian 函数,得到光伏功率数据样本的近似表达式为
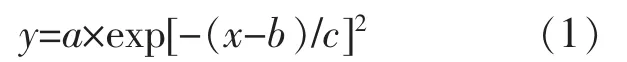
式中:y 为光伏功率数据;a,b,c 为拟合参数。
②逐渐改变拟合表达式中c 的大小, 使上包络线y1与下包络y2之间的数据约为整个实测数据的99%, 得到区间宽度Δc,Δc=|c1-c2|,c1,c2分别为上、 下包络线的拟合参数,y1,y2的计算式分别为
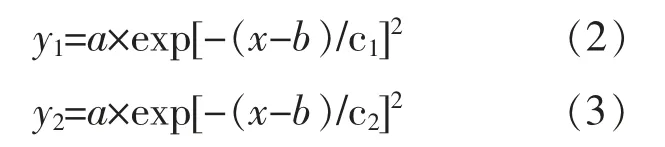
③设光伏功率数据的3 个数字特征Ex=b,En=c,He=Δc/3。
④由云模型熵Enw和超熵Hew生成正态随机熵为En2′=N(En,H)。
⑤求得一定太阳辐照度下的功率云滴gi。 gi的计算式为
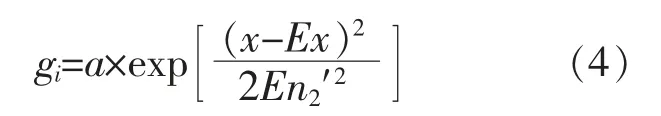
⑥重复步骤④,⑤,直至生成各太阳辐照度下的功率云滴。
为了更加精确地包裹样本数据,拟合曲线n(x)、上界函数h(x)和下界函数d(x)不采用同一种拟合函数。 通常,Hew为一个定值,Hew=c/3。 上、下包络线的正态随机熵Hes(x),Hed(x)的计算式分别为
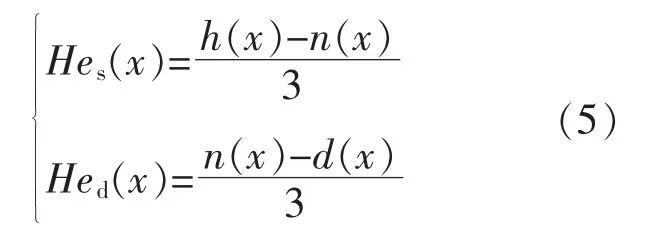
本文参照文献[15] 提供的理想光伏功率模型,确定了某一特定太阳辐照度x1,在该太阳辐照度下光伏出力与光照强度的关系开始由非线性关系变为线性关系;此外,还确定了另一特定太阳辐照度x2, 在该太阳辐照度下光伏出力与光照强度的线性相关性减弱。x1,x2分别为400,1 000 W/m2。
根据上述参数, 将太阳辐照度-光伏功率散点分为3 个云分段:当x∈[24,x1)时,太阳辐照度-光伏功率数据为下分段, 最小输出功率所对应的太阳辐照度为24 W/m2;当x ∈[x1,x2)时,太阳辐照度-光伏功率散点数据为中分段; 当x∈[x2,1 270)时,太阳辐照度-光伏功率散点数据为上分段。
本文所采用的的包络函数为高斯函数G(x)和线性函数P(x),二者的计算式分别为
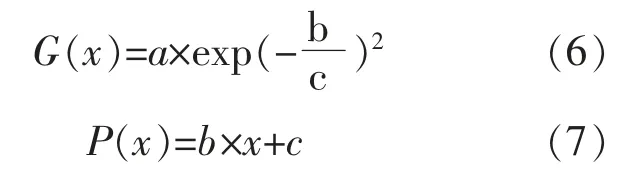
光伏功率数据归一化后, 对各云分段进行拟合, 为了满足实验要求以及剔除部分异常光伏功率数据,本文以包络率为99%作为指标,得到拟合参数值,并分别用P(b,c)和G(a,b,c)表示各云分段的上、下包络线,所用函数及参数如表1 所示。

表1 各云分段拟合或包络函数表Table 1 Table of segmentation fit or envelope function
基于表1 的拟合包络结果对光伏功率数据进行实际的拟合、包络,得到的结果如图3 所示。
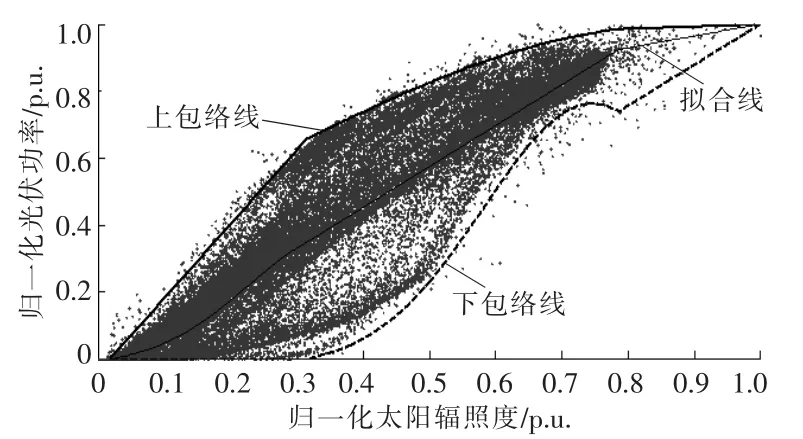
图3 利用拟合包络得到的光伏功率随太阳辐照度的分布图Fig.3 Distribution map of photovoltaic power with solar irradiance obtained by fitting envelope
当包络率为99.35%时, 传统云分段模型算法结果如图4 所示。
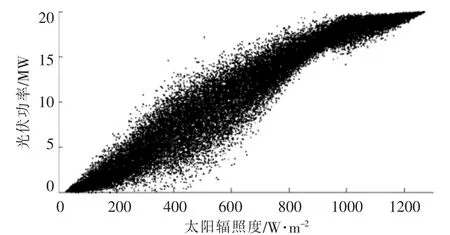
图4 当包络率为99.35%时,传统云分段模拟结果Fig.4 When the envelope rate is 99.35%, the result of trad itional cloud segmentation simulation
由图3,4 可知, 云模型结果并不能表示出太阳辐照度-光伏功率散点的聚散程度。
3 基于改进云分段模型的缺失数据补齐方法
本文基于Copula 理论的随机熵算法提出了不同光伏功率数据片段的云分段模型算法如下。
①对光伏功率数据样本的散点进行分段,得到光伏功率数据样本的近似拟合表达式n(x),同时,进行上包络线表达式h(x)与下包络线表达式d(x)的拟合,使包络率在99%以上。
②将实际的光伏功率数据样本的散点分成上包络点与下包络点, 各云分段的太阳辐照度和光伏功率归一化后, 求取太阳辐照度和光伏功率分布函数的联合经验函数 (具体模型见文献[16]),从而得到特定太阳辐照度下光伏功率的条件概率分布。
③依照条件概率分布确定所需要的2 个熵:hiu(x),hid(x),其中,i∈[1,N],N 为云滴数,N 由包络线与拟合线之间的宽度决定。
④设正态随机常数ki=|N(0,1)|,该常数表征由于光伏功率存在复杂的影响因素导致自身产生随机性。
⑤计算不同太阳辐照度条件下的功率云滴,以一次函数为例,上、下包络线的云滴数表达式分别为
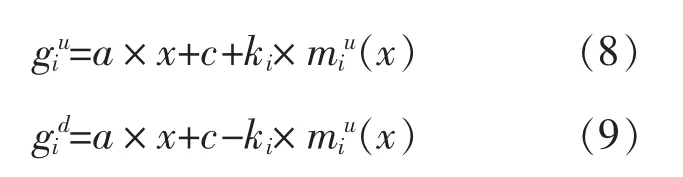
⑥重复步骤④,⑤,直至生成各太阳辐照度下的光伏功率云滴。
以中分段的上包络点为例,太阳辐照度与光伏功率归一化后的联合经验函数值如图5所示。
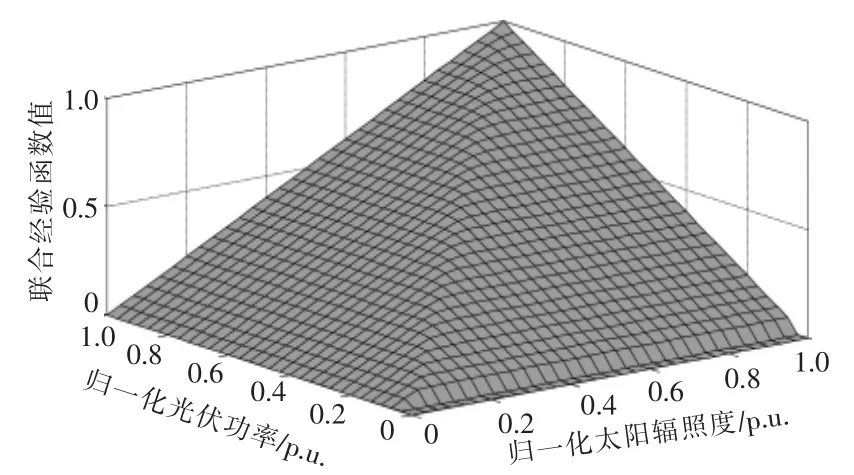
图5 中分段上包络点联合经验分布Fig.5 Joint empirical distribution of envelope points on mid-segment
改进云分段模型的计算结果如图6 所示。 由图6 可知, 改进的云分段模型更加符合实际光伏功率散点分布特征。 改进云分段模型能得到完整的光伏功率散点条件概率分布密度P (gi|xi)。 其中:xi为不同时间点的太阳辐照度i ∈N+。
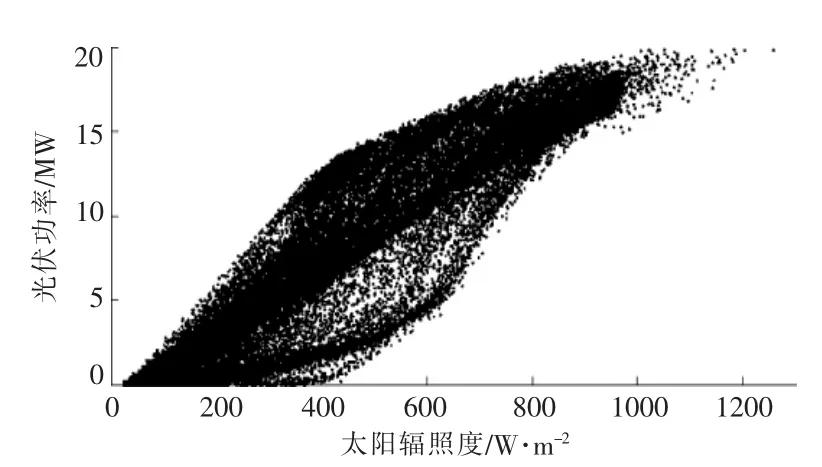
图6 改进云分段模型结果Fig.6 Result of improve segmentation cloud model
设光伏功率数据缺失片段的数据点为(xk,gk),其中,k∈N+。 假设在光伏功率数据采集过程中,太阳辐照度数据完整且正确,即xk已知,gk未知,构建缺失数据补齐模型为
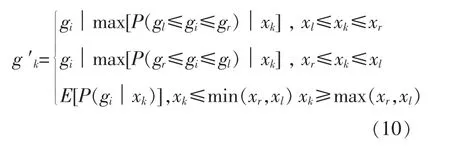
式中:(xl,xr) 为该缺失数据左侧最接近已知光伏功率的散点;(xr,xl) 为缺失数据右侧最接近已知光伏功率的散点;E[P(gi│xk)]为特定太阳辐照度下光伏功率散点的期望;g′k为光伏功率补齐的功率值。 该模型能够针对不同波动性的缺失数据片段进行特定方法补齐。
4 算例分析
将光伏功率缺失数据补齐后,利用本文提出的方法、 滑动平均法、 传统云模型和BP 神经网络补齐方法同时对一定比例的光伏功率缺失数据进行补齐[17]。传统云模型的补齐方法通过传统云分段模型得到功光伏功率条件概率分布结果,然后通过式(3)补齐光伏功率缺失数据。BP 神经网络方法将数据归一化后,以太阳辐照度作为输入, 光伏功率作为输出,利用历史完整光伏功率数据作为训练集。通过平均相对误差和准确率对光伏功率数据补齐效果进行评价。
w 的表达式为
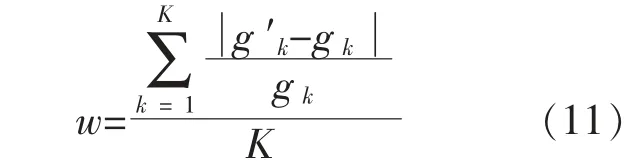
r 的表达式为
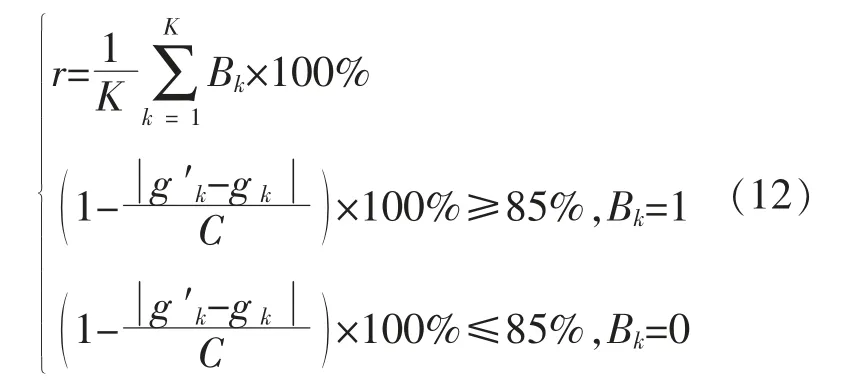
式中:gk为缺失的功率值;g′k为补齐的功率值;C为装机容量;K 为缺失数据的个数。
本文对10%,20%和30%的光伏功率数据进行随机缺失和连续缺失。 利用不同方法对20%的光伏功率随机、连续缺失数据进行补齐,结果分别如图7,8 所示。
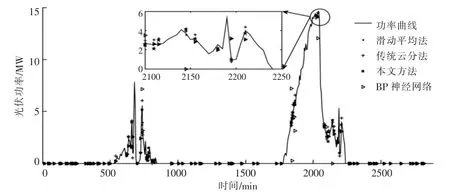
图7 对20%光伏功率随机缺失数据进行补齐的结果图Fig.7 Figure of the result which completes random missing data for 20% PV power

图8 对20%光伏功率连续缺失数据进行补齐的结果图Fig.8 Figure of the result which completes continuousmissing data for 20% PV power
由图7,8 可知,与其他3 种方法相比,对于光伏功率数据的随机缺失和连续缺失, 本文方法的数据补齐结果,更加贴近实际光伏功率。
对于不同缺失条件下的补齐结果, 计算出各个方法补齐光伏数据的平均相对误差和准确率,如表3 所示。
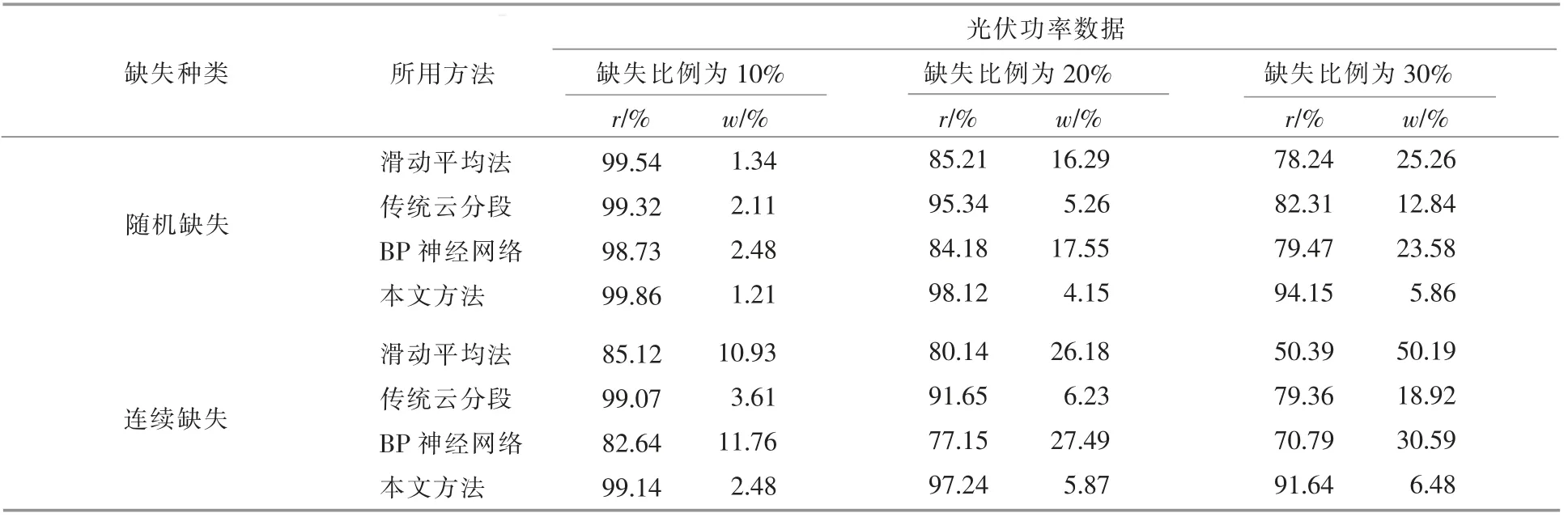
表3 不同缺失条件下,不同方法补齐光伏数据的平均相对误差和准确率Table 3 Under the circumstance of different data missing, each method evaluates index statistics
由表3 可知, 随着光伏功率数据缺失比例的增大,数据补齐的难度也在增大;光伏功率数据随机缺失的补齐效果优于连续缺失的补齐效果。 滑动平均法对小比例光伏功率数据随机缺失的补齐效果较好 (光伏功率数据缺失率为10%的情况下,准确率为99.54%),但由于该方法仅依靠光伏功率数据缺失片段左右的2 个数据,随着光伏功率数据随机缺失比例的增大,该方法的补齐效果逐渐变差; 在光伏功率数据连续缺失情况下,该方法表现出严重的不适应性, 误识别率达到10%以上。 对于传统云分段模型数据补齐方法,数据补齐效果的稳定性优于滑动平均法,但在大比例光伏功率数据缺失的情况下(数据缺失率为30%),该方法的准确率低于83%,误识别率高于13%。 对于BP 神经网络方法在大比例光伏功率数据缺失情况下(数据缺失率为30%),数据补齐效果的准确性(参照准确率)和稳定性(参照平均相对误差)略优于滑动平均法,但其他方法的数据补齐效果的准确性和稳定性都低于传统云分段方法和本文方法。 对于本文所用的方法,在不同光伏功率数据缺失情况下,数据补齐效果优于其他3 种方法,在30%光伏功率数据缺失的情况下,数据补齐的准确率高于94%,误识别率低于5.9%;对于30%光伏功率数据连续缺失情况下,数据补齐的准确率高于91%, 误识别率低于6.5%。 综上可知,本文方法对光伏功率缺失数据补齐效果有一定的提高。
5 结术语
①在光伏电站实际运行中, 光伏功率缺失数据阻碍了光伏功率的相关研究。 对于不同研究对象,采用的数据补齐方法不同,因此,对光伏功率缺失数据的补齐方法须进行特定研究。
②正向云分段模型体现了太阳辐照度-光伏功率散点的分布界限, 但特定太阳辐照度下光伏功率分布特点并不适合用正态随机熵进行描述。本文通过对各分段太阳辐照度与光伏功率的分布构建联合经验函数, 对光伏功率条件概率分布进行拟合,结合云分段模型的随机熵理论,改进了对太阳辐照度-光伏功率散点分布特点的描述。
③本文基于改进的云分段模型的结果能够得到符合光伏功率数据分布特点的条件概率分布,根据该条件概率分布并考虑数据缺失片段的波动性建立了缺失数据的补齐模型,分析结果表明,本文方法对比传统云模型、 均值法和BP 神经网络方法更具有效性和实用性。
