基于均匀分布阵列的海上多能联合发电规划及优化

刘 宁， 米志伟， 刘 栋， 谷怀广， 魏书荣

（1.上海电力大学 电气工程学院， 上海 200090； 2.国家电网全球能源互联网研究院有限公司， 北京102209）

0 前言

随着化石能源的日渐枯竭，以风能为代表的新能源备受关注。 我国海上风能储量丰富，海上风电技术发展迅猛，但在海上风电巨大发展潜力下仍存在制约其发展的阻力。海上风机可及性较差，导致其运维便利性降低，使海上风电场的运维成本约为同等容量陆地风电场的2 倍[1]。 目前，海上风电场运维成本约占全寿命周期成本的23%左右[2]。 因此，合理规划海上风电场的运行维护， 对降低海上风电场运维成本， 提高现有海上风电场的可用性具有重要意义。当前，针对海上风机运维的研究主要集中在设计新型运维监测系统、 开发运维策略和研究风电场运维后勤管理优化方法[3]。 然而，这些研究仅考虑了对风电场的自身运维， 并未统筹考虑联合场内其他资源来提高风电场运维的便利性。波浪能发电作为风能的衍生能源发电方式，具有装置多样、 安装便利和操作简易等优点，其商用占比逐年提升。 研究显示，风能与波浪能联合发电可有效降低风电场区内部综合波高，改善风机可及性，提升风电场运维便利性[4]～[6]。

风浪能联合发电包括两种形式：混合系统发电形式和共存系统发电形式[7]。

混合系统发电形式的研究主要针对两种装置的结合形式进行风浪装置一体化设计[8]，[9]。 然而，针对目前已投运的海上风电场，在原来基础上进行风浪联合发电规划属于非同期联合发电规划，其选址及应用存在一定的局限性，研制及架设费用过于昂贵， 很难在实际工程应用中满足经济性要求。

共存系统发电形式是通过相同并网设备将波浪能装置与场区内的风机并网。这种发电形式既能够降低投资成本， 保证联合发电经济性，又不会对原有风电场发电形式产生干扰， 因此，对非同期的联合发电规划影响程度较低，是今后风浪联合发电的主要形式。 目前，共存系统联合发电形式主要集中于外围分布阵列（PDA）[7]。 文献[10]研究了在外围分布阵列形式下，不同阵列布局间波浪能发电场与风电场协同作用对风电场运维便利性的影响。 文献[11]，[12]针对外围分布阵列布局下多能联合发电系统的风电场阴影效应进行研究，通过量化指标研究了波浪能发电场产生的阴影效应对风电场波高降低的影响程度。上述研究均未兼顾风电场内单台风机受波高影响程度和风浪联合发电系统的经济性。波高是影响波浪力数值的主要因素，当场区内波高超过一定数值时，风机运维船只受波浪力的影响无法进入风电场区内部，此时出现故障的风机机组将得不到有效维护。 此外，波高的变化也会改变波浪能装置的输出功率，对风浪联合发电的经济性产生影响。 目前，兼顾海上风电场运维可靠性和经济性的规划方法尚待研究。

针对上述问题， 本文基于均匀分布阵列（UDA） 提出一种海上多能联合发电规划及优化方法， 在考虑经济性和可靠性指标的基础上，增加波高降低百分比指标来共同衡量方案的最优性，以此满足海上风电场运维需求。 通过建立风机与波浪能装置间的最优布局， 以度电成本、等效停运率和波高降低百分比为量化指标，验证了本文规划及优化方法对现有海上风电场经济性和可靠性的提升程度，为海上多能联合发电规划提供参考思路。

1 联合发电并网方式的选取

均匀分布阵列是基于已投运的海上风电场，对场区内所有风机采用相对统一的布局方式进行波浪能装置布置。在采用均匀分布阵列布局方式进行风浪联合规划及优化之前，须研究风机和波浪能装置并网的可行性。首先对风机与波浪能装置间海缆连接位置进行研究，并分析其装置间的并网方式。 风机与波浪能装置相关布局如图1所示。

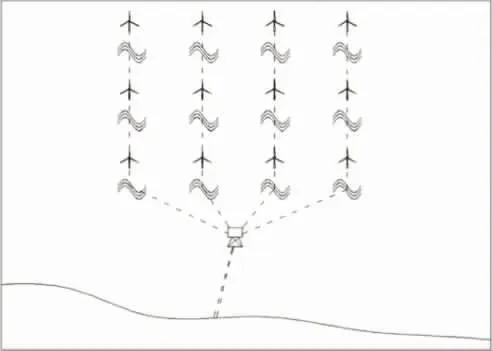
图1 风机与波浪能装置相关布局图Fig.1 Layout of offshore wind turbine and wave energy device

根据波浪能装置出口连接位置，可将风机与波浪能发电装置间的并网方式分为两种 （图2）。第一种并网方式是对波浪能装置配置独立的升压变压器及线路，将波浪能装置产生的电能升压后输送至中压汇流母线。 第二种并网方式是通过小型变压器将波浪能装置并网于风机低压侧，再通过风机箱式变压器进行升压，将电能送至中压汇流母线。

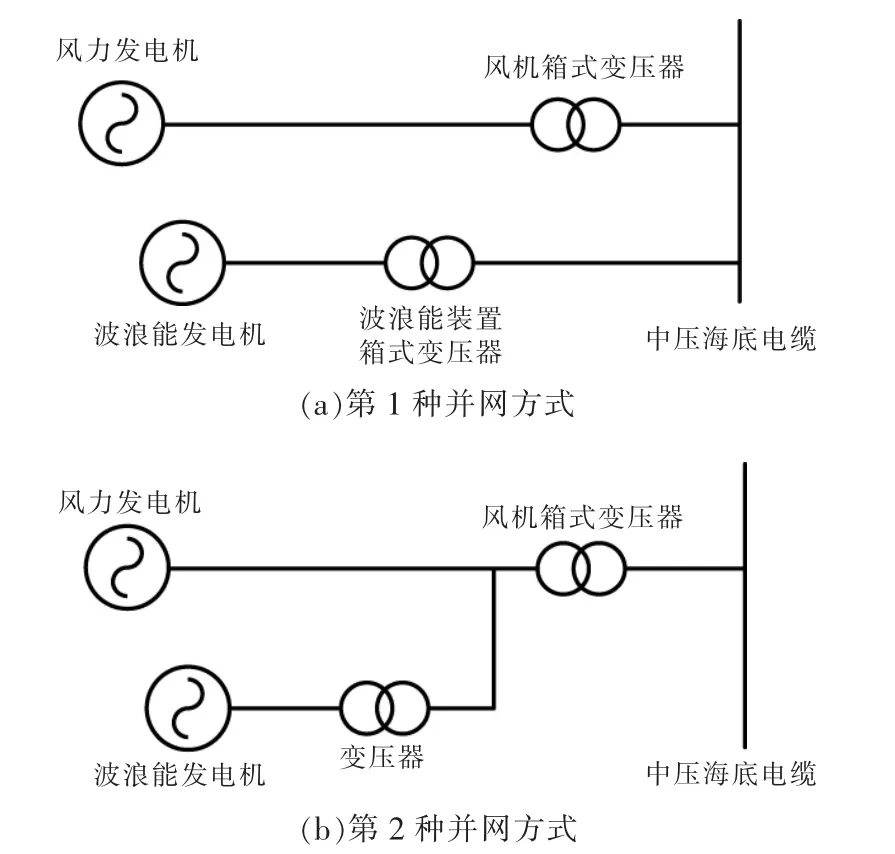
图2 装置间并网方式Fig.2 Parallel operation between devices

为选择风机与波浪能装置间合适的并网方式，须进一步分析两种并网方式的抗扰动能力，相关故障设置参考文献[13]。 图3 为不同扰动情况下的系统功率波动图。 其中，图3（a）为小扰动下的有功动态响应图，图3（b）为大扰动下的有功动态响应图。 在小扰动仿真中， 设置系统电压跌落0.04 p.u.，时间为0.02 s。 在大扰动仿真中，设置输电线路中一条线路发生接地故障， 故障接地阻抗为9 Ω，0.03 s 后故障切除。

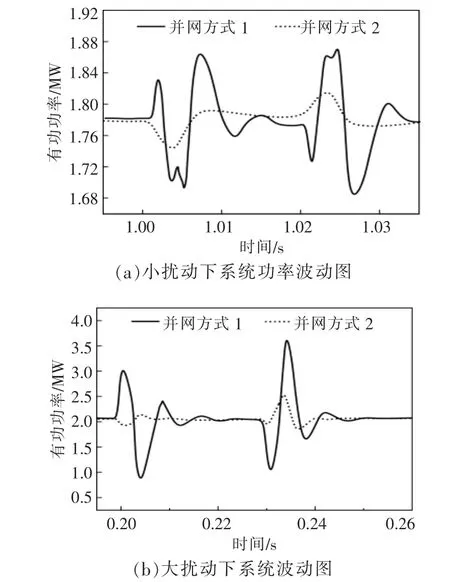
图3 扰动下系统功率波动图Fig.3 Power fluctuation diagram of a combined power generation system under disturbance

如图3 所示， 第2 种并网方式在两种不同扰动状况下，均具有较高的稳定性。 另外，考虑利用已投运的海上风电场进行联合发电， 第一种并网方式的工程可操作性较低。在正常运行风电场中，波浪能装置采用与风机相同方式接入海底电缆，须对输电海缆进行切割并增加分接头装置， 增大了故障几率，同时降低联合发电的经济性。 因此，本文中联合发电装置选取第2 种并网方式进行连接，并对并网后的布局进行规划分析。

2 联合发电规划及优化方法

分析不同布局方式下风机和波浪能装置所能承受的波浪力强度，以此来优化两者的相对布局，可在保证风机所受波浪力最低的基础上， 提高联合发电的经济性和可靠性。

2.1 联合发电布局规划

在海域中，波浪遇到障碍物时会发生绕射、折射等现象，使得障碍物后方区域波高发生变化，影响波浪力强度。因此，对风浪装置间相对布局进行分析，须首先研究这种情况下波高的变化情况。

装置相对布局如图4 所示。 图中：θ 为入射波与水平夹角；ai为波浪能发电装置浮子i 的半径；ak为风机k 的机筒半径；Lik为装置间距；α 为装置间连线与水平夹角。

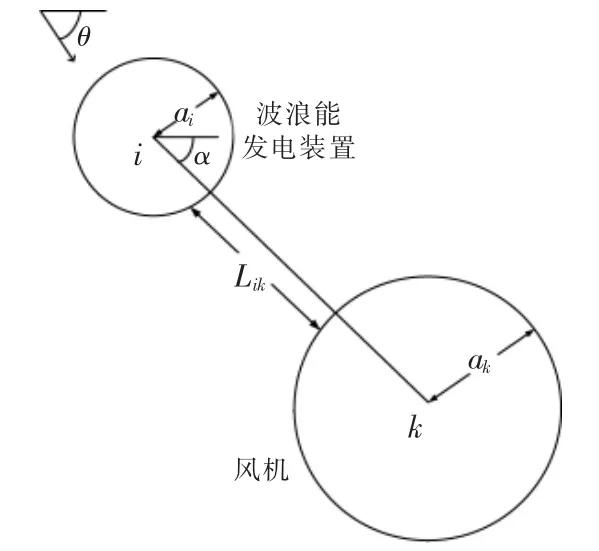
图4 装置间相对位置布局图Fig.4 Layout diagram of corresponding positions between devices

当风机和波浪能装置等效的圆柱体尺寸不同且距离较近时，受迎波面装置的影响，背波面的波高将发生变化， 导致背波面装置所受波浪力发生变化[14]。 引入入射波速度势对背波面装置所受波浪力进行分析，其表达式如下：

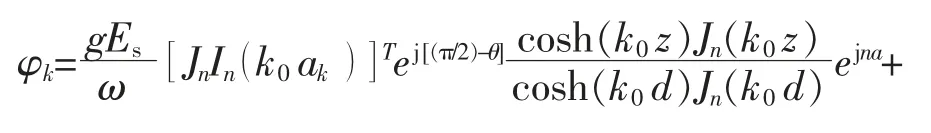
式中：g 为重力加速度；Es为波高；ω 为角频率；n为阶数；Jn为第一类Bessel 函数；In为第一类修正Bessel 函数；k0为入射波的波数；z 为波浪能浮子底部距离海底的高度；d 为水深；Hn为第一类Hankel 函数；β 为θ 与α 的差值角；f 为风机处受波浪入射角对应的阶数。

在装置型号尺寸及所处海域固定的情况下，即z 与d 为常数时，对式（1）进行化简可得：

式中：W 为与装置及海域有关参数；x=k0Lik为Hankel 函数自变量；Hn由第一类Bessel 函数Jn（x）和第二类Bessel 函数Yn（x）共同构成：

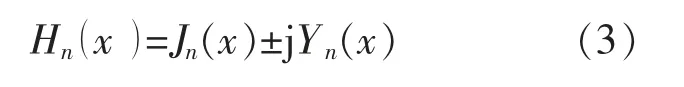
Bessel 函数曲线如图5 所示。

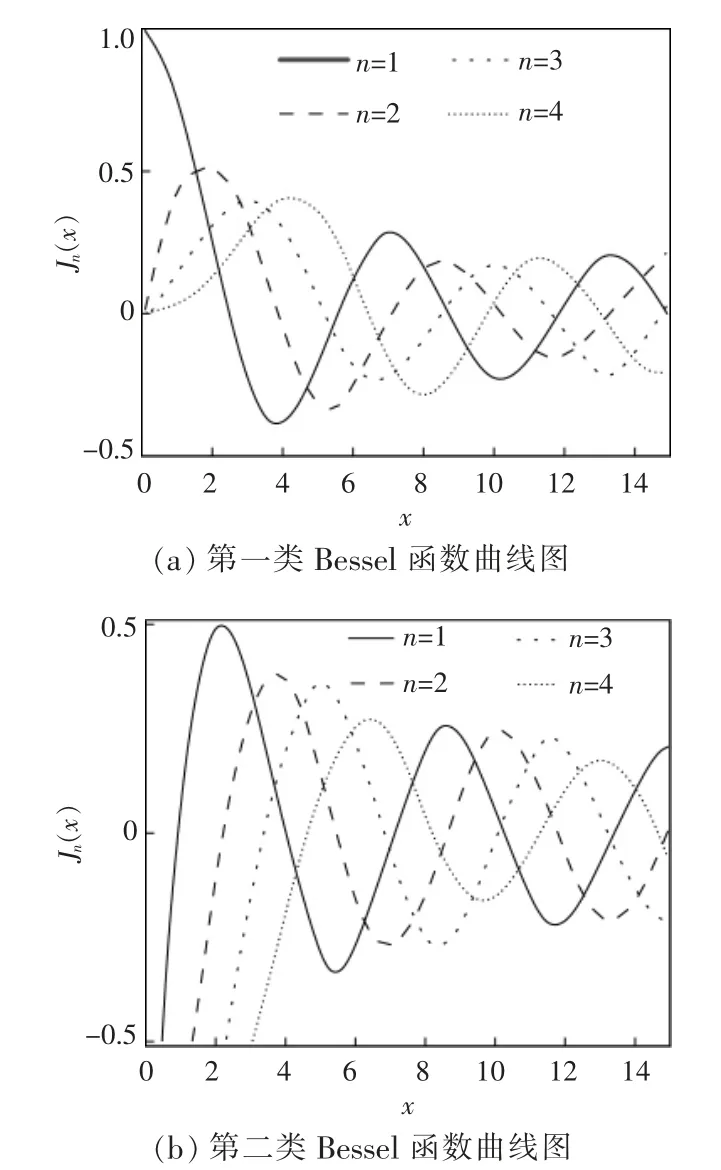
图5 Bessel 函数曲线图Fig.5 Graph of bessel function

在理想海域下，入射波波数k0及波浪入射角度不发生变化，x 主要由装置间距Lij决定。 考虑到曲线波动幅度的有效性，本文Hankel 函数中阶数n 选取1。由图5 可知，当x＜10 时，Hn（x）振幅有效值随x 发生变化，结合式（2）可知影响速度势的因素为间距和装置间差值角；当x＞10 时，Hn（x）振幅有效值不发生变化。 由此可知，间距对速度势的影响较小，影响速度势的主要因素为装置间差值角。

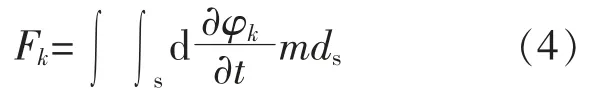
式中：m 为单位外法矢量；Fk为风机所受波浪力；t 为时间变量。

联立式（2），（4）进行分析可知，在风机位置及海域固定时，风机所承受的波浪力由装置间距Lik和装置间差值角度β 决定。

本文案例在装置相对布局不同的情况下，分析波浪冲击对风机和波浪能装置的影响。其中，装置相对布局是由间隙比和差值角确定的。 间隙比定义如下：

2.2 计及最优布局的联合发电模型

本文提出的计及最优布局的联合发电模型中，考虑系统经济性、可靠性和风机可及性，分别选取度电成本、 等值停运率和波高降低百分比作为衡量方案优劣的指标。

度电成本作为衡量方案经济性的指标， 其定义如下：

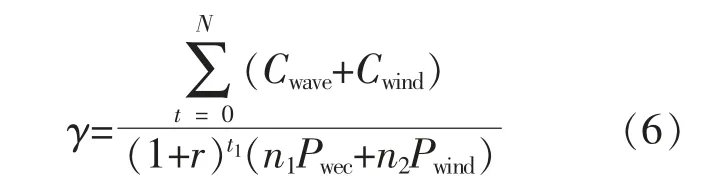
式中：γ 为度电成本；Cwave为生命周期内波浪能装置总成本；Cwind为生命周期内风机总成本；t1为生命周期总时间；r 为折现率；n1为波浪能装置数量；n2为风机数；Pwec为生命周期内波浪能装置产生的总能量；Pwind为风电场生命周期内输出总功率。

度电成本中成本模型由波浪能装置总成本和风电场总成本构成。

式中：Cwecequipment为波浪能装置费用；Cwecmaintenance为波浪能装置运维费用。

风电场总成本由风机费用和风电场运维费用构成：

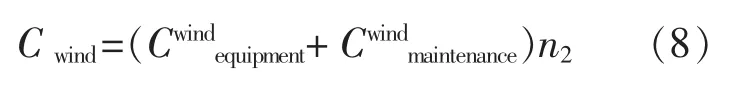
式中：Cwindequipment为风电场风机费用；Cwindmaintenance为风电场运维费用。

忽略投资费用随时间的变化，引入折现率，将风机费用和风电场运维费成本后续费用折算至第一年进行计算。

度电成本中的功率模型由波浪能装置模型和风机功率模型构成。

波浪能装置模型[15]：

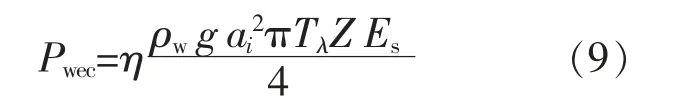
式中：η 为波浪能装置整机转换系数；ρw为水密度；ai为浮子半径；Tλ为与波长有关的参数；Z 为与浮子震荡运动振幅有关的参数；Es为波高。

风电场输出功率模型：

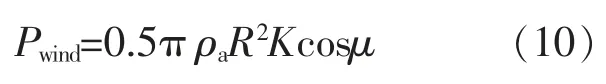
式中：ρa为空气密度；R 为桨叶半径；K 为风能利用系数；μ 为偏航角。

等值停运率作为衡量联合发电线路可靠性的指标，定义如下：

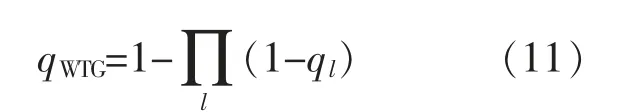
式中：ql为图2中各元件的停运概率。

在模型中，装置间距及差值角均固定，装置所受波浪力仅由波高决定。 利用风电场区内波浪观测站对风机装置处联合发电前后的波高进行数据采集， 引入波高降低百分比作为风机所受波浪力降低水平的指标。

波高降低百分比定义如下：

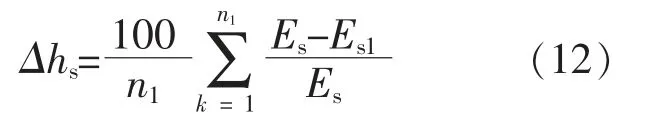
式中：Es为风电场风机处原波高；Es1为联合发电后风机处波高。

3 算例分析

将已投运的某海上风电场作为案例进行分析，利用matlab 编写相应程序，对接入波浪能装置的海上风电场进行仿真建模。 该海上风电场一期包括34 台3 MW 海上风电机组，相关风机参数如表1 所示。已知该风电场运维成本、风机输出功率和投运年限。 联合发电的250 kW 振荡浮子式发电装置输出参数参考文献[16]。 根据所查阅的风电场数据和所选波浪能装置的参数可知， 单台风机仅能满足1 台波浪能装置的并网需求。 利用海域波浪观测站采集的数据分析年综合流向，采用频率较高的角度作为波浪入射角θ。 同时利用波浪观测站对场内波高采样，区域采样间隔为5 m，周期为2 min。

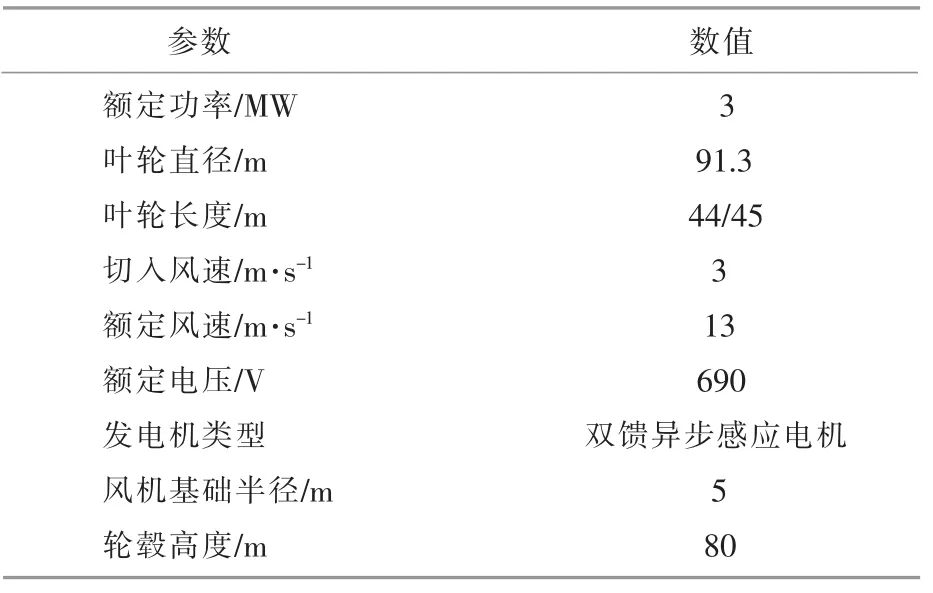
表1 海上风电场风机参数表Table 1 Wind turbine parameters for offshore wind farm

3.1 最优布局仿真分析

在两装置间距和差值角不同的情况下， 为了解风机与波浪能装置所受波浪力的冲击程度，引入双柱绕流模型进行装置所受波浪力的分析。 利用ANSYS FLUENT 流体软件进行海洋多圆柱绕流建模，相关参数的设定参考文献[17]。

在波高为常数的理想海域情况下， 通过对两种装置的不同间距及差值角的受力研究， 选取其最优布局。两装置可等效为两直径不等的圆柱，其中波浪能装置等效为半径3 m 圆柱， 风机等效为半径5 m 圆柱。 本文主要考虑层流影响，模型雷诺数设定为500，水流流速设定为1 m/s。 当装置间距较大时，装置间距对其所受波浪力的影响较小。为保证间距的影响不超出波浪力对装置的影响范围，选取间隙比ε为0.5，1.0，2.0，3.0，∞，（其中，ε=∞， 可看作原有风电场运行方式下风机所受波浪力），选取差值角β为0，45，90，135，180°。 本算例利用5种差值角与4 种间隙比对装置的受力情况进行建模分析。 图6（a）～（e）为差值角0，45，90，135，180° 下的装置布置图。 图7 为差值角在0～180°和不同间隙比下，风机与波浪能装置所受波浪力的变化趋势拟合曲线。

图6 不同间隙比、差值角下装置相对布局图Fig.6 Graph of relative layout of devices with different spacing ratio and difference angle

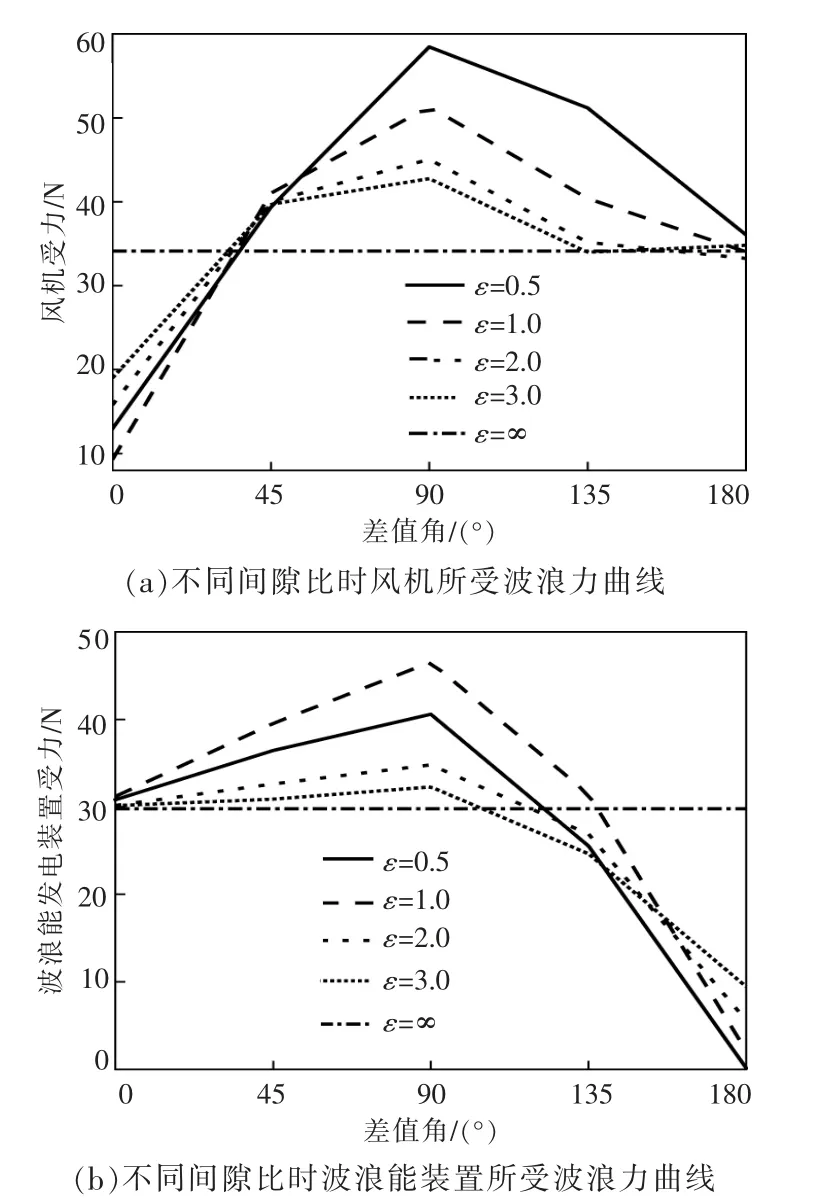
图7 不同间隙比、差值角时装置所受波浪力曲线图Fig.7 Graph of wave force on wind turbine and wave energy device under different clearance ratio and difference angle

由图7（a）可知，在4 种不同间隙比情况下，风机所受波浪力均随着差值角的增大而呈现先增大后降低的趋势。对比4 种间隙比与间隙比ε=∞时风机所受波浪力曲线可知， 仅在差值角为0～45°时，风机在4 种间隙比下所受波浪力均小于间隙比ε=∞时所受的波浪力，故仅分析差值角为0～45°的最优间隙比。通过分析可得，当装置间隙比ε=1时，风机所受波浪力最小，具有较好的可及性。

由图7（b）可知，在4 种不同间隙比情况下，波浪能装置所受波浪力均随着差值角的增大呈现先增大后减小的趋势。 结合图7（a）分析可知，差值角为0～45°时，4 种间隙比下风机均具有较好的可及性。在此基础上，进一步分析波浪能装置的受力情况。 由图7（b）拟合曲线可知，当差值角为0～45°时，4 种间隙比下的波浪能装置所受波浪力均大于波浪能装置独立运行时所受的波浪力。 由此可知，当间隙比ε=1 时，波浪能装置受力最大，具有较好的发电效率。

通过以上对风机与波浪能装置受力拟合曲线分析可得，当差值角β=0°、间隙比ε=1 时，联合发电系统具有较好的风机可及性和经济性。 采用上述差值角和间隙比对波浪能装置及风机进行组合，联合发电拓扑如图8 所示。

图8 计及影响因素的联合发电最优拓扑图Fig.8 Graph of optimal topology of combined generation with consideration of influencing factors

3.2 布局优势分析

为进一步证实本文所提模型的有效性， 采取4 种布局方式进行对比分析。 布局方式A：差值角β=0°，间隙比ε=1；对比布局B：差值角β=0°，间隙比ε=0.5；对比布局C：差值角β=45 °，间隙比ε=0.5；布局方式D 即原有风电场。将布局方式A，B，C 和原风电场D 进行对比分析， 其中装置、隔离开关等元件的故障率参考文献[18]。 联合发电布局如图9 所示。

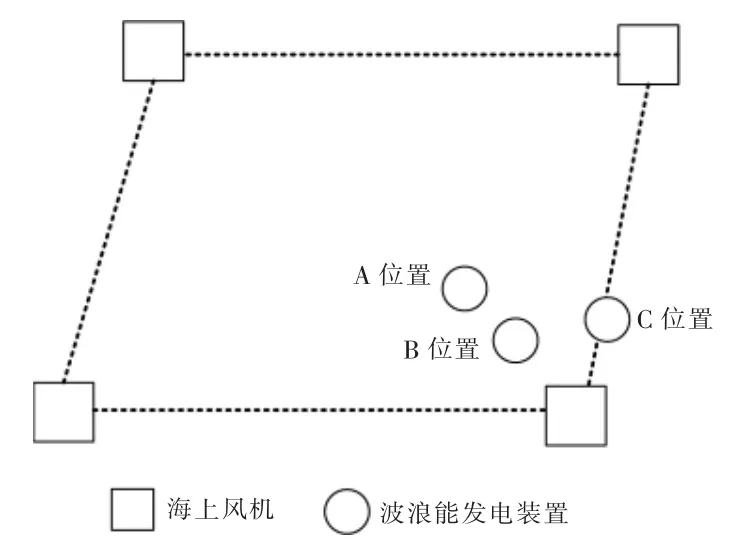
图9 联合发电布局图Fig.9 Graph of corresponding layout with combined power generation

利用本文提出的联合发电规划方法， 结合观测站观测信息分析联合发电情况。 A，B，C 3 种布局的度电成本、 等值停运率和波高降低百分比的计算结果见表2。

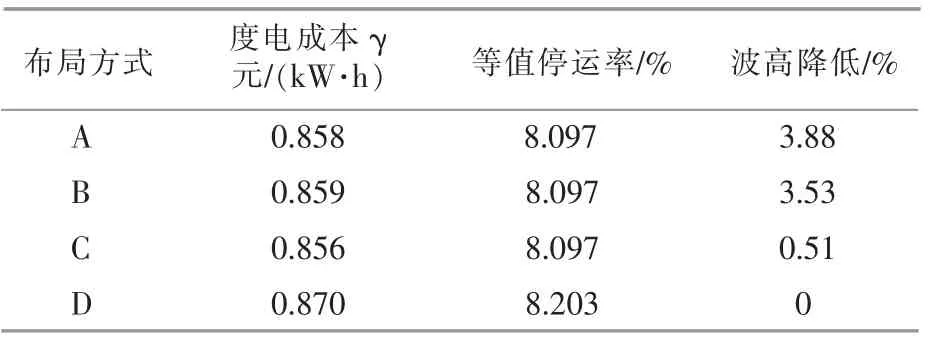
表2 联合发电布置方案结果对比Table 2 Comparison of results of combined power generation layout scheme

通过仿真分析所得结果如下。

①A，B，C 3 种布局方式均降低了系统的度电成本。3 种布局方式具有相同的并网方式、装置数量以及并网设备， 因此3 种方案全寿命周期内的总费用较为接近。但是，波浪能装置与风机间不同的布局方式会导致波浪能装置所受波浪力不同，从而影响系统总输出功率，最终导致度电成本的改变。 其中，布局方式A 和B 比原风电场D 的度电成本降低约1.38%， 布局方式C 比原风电场D 的度电成本约降低1.6%。

②A，B，C 3 种布局方式均降低了系统的等值停运率。 采用风机箱式变压器低压侧并网的连接方式， 布局方式A，B，C 具有相同的等值停运率，比原发电方式的等值停运率降低了1.3%。

③布局方式A 可最大程度地降低风机所受波浪力，提高风机的可及性，降低系统维护成本。在仅1 台波浪能装置并网的情况下， 采用布局方式A 的风机所受波浪波高比原风电场D 减少3.88%, 比布局方式B 的波浪波高降低率增加了0.35%；采用布局方式C 时，风机所受波浪波高与原风电场运行时风机所受波浪波高接近， 波高降低程度较小，可忽略不计。

对比联合发电度电成本、 等值停运率以及波高降低百分比可知， 本文所提出的联合发电方案在经济性和可靠性方面均比原发电方案具有更明显得优势。 因此，在选择合理布局方式的前提下，本文所提方案能够有效降低系统的维护成本。

4 结束语

本文针对已投运的海上风电场， 提出一种规划及优化波浪能装置布局方案， 在改善海上风电场运维便利性的基础上， 提高联合发电经济性及可靠性， 为提升海上风电场多能联合发电规划提出了新方法。

通过扰动试验分析了装置并网方式， 验证了波浪能装置通过小型变压器并网于风机低压侧为最优并网方式。 针对不同工况下的装置布局进行建模， 分析风机与波浪能装置间相对布局对风机与波浪能装置所受波浪力的影响程度， 得到了风机与波浪能装置间最优布局时的差值角和间隙比。 本文还分析了不同情况下联合发电的影响因素， 验证了所提出的规划及优化方法可提升现有海上风电场的经济性和可靠性。