考虑水火电多场景协调的电力系统阻尼优化控制模型
2020-12-16潘晓杰张文朝徐友平边宏宇朱思宇张立伟
潘晓杰, 张文朝, 徐友平, 边宏宇, 朱思宇, 张立伟
(1.国家电网公司华中分部, 湖北 武汉 430077; 2.北京科东电力控制系统有限责任公司, 北京100192; 3.华北电力大学, 河北 保定 071003)
0 引言
随着风电、光伏等非同步发电系统并网规模的不断扩大,水电机组作为可再生能源的同步发电系统,在电力系统安全稳定控制中成为系统惯性和阻尼特性调节的关键环节。 我国水电装机的选址大多处于远离负荷中心的水利资源富集区,使水电具有大容量、长距离的特点,对电力系统静态、暂态稳定和系统动态振荡问题的影响也很突 出[1]~[4]。
目前,国内外针对电力系统稳定和振荡问题的研究,大多通过电力系统稳定器(PSS)来抑制励磁高增益带来的负阻尼转矩[5],[6]。受临界增益的限制,电力系统稳定器的正阻尼补偿效果在较多应用场景下受到影响。 水电机组励磁系统一般采用较高增益控制参数以提高其暂态响应特性,这种控制方式易使励磁系统产生负阻尼特性[7]~[9]。针对常规水电机组和抽蓄水电机组占比相对较高的电网,将水电励磁参数与网内火电机组励磁参数协调优化,根据电网运行状态的不同场景对系统总阻尼参数进行优化控制,可有效提高电网动态稳定性能及水电、风电、光伏与火电打捆远距离输送能力。
励磁控制系统动态增益直接影响发电机的电压动态响应速度, 改变增益有利于提高发电机动态性能和阻尼效果, 而且励磁系统动态增益也会影响发电机暂态稳定性[10]。 绝大部分水轮发电机均为自并励励磁系统,在工程实际当中, 往往将励磁系统的动态增益与暂态增益设为相同。 目前,对励磁系统动态增益影响发电机暂态稳定的认识上仍然存在模糊之处。 文献[11],[12]重点分析了非线性控制等不同控制方式对系统暂态稳定的影响, 但是对机组广泛采用的励磁比例-积分-微分(PID)控制参数影响尚未进行具体和深入的研究。 文献[13],[14]提出了励磁增益越大对暂态稳定越有利的观点。
本文通过分析励磁系统的控制原理及参数要求,研究励磁增益对系统静态稳定极限、暂态稳定极限和动态稳定极限的影响, 提出了基于自并励励磁系统的水火电协调电力系统励磁控制系统模型;在水火电协调励磁系统模型基础上,研究了多水电机组和多火电机组的电力系统转子运动方程及其阻尼参数优化控制模型;以多场景扰动下的电力系统整体能量不平衡量最小为优化目标,建立了基于阻尼优化控制的励磁系统参数优化策略模型及其求解算法。 本文以华中某电网的实际运行数据建立算例仿真模型。 仿真结果表明,该水火电协调阻尼优化控制模型能够对主导振荡模式下的水电、火电机组励磁参数协调优化,有效地提高水电、火电协调励磁调节场景下的暂态稳定性和动态稳定性。
1 水火电协调励磁调节模型
水电机组与火电机组协调励磁拓扑结构如图1 所示。 当电力系统进入稳态小扰动、暂态大扰动或动态振荡过程时, 系统内的水电机组快速励磁响应与火电机组励磁响应系统根据扰动能量、功角、 电压等输入信息和各自的励磁响应能力进行信息交互,实现系统总励磁参数的协调优化调节,为系统提供最佳的阻尼系数, 提高系统稳定性能和振荡抑制能力。
图2 为进行阻尼优化控制的自并励励磁系统模型。 图中:VERR为电压偏差信号;VS为目标电压信号;K 为水电或火电励磁电压响应比例参 数;T1,T2,T3,T4为 水 电 或 火 电 机 组 励 磁 响 应各环节延迟参数;KV为励磁响应环节积分参数;KA,TA为调压环节电压变化速率参数和电压变化延迟参数;KF,TF为调压环节稳定控制比例参数和稳定控制延迟参数; VL为低励约束参数;VH为过励约束参数;EFD为励磁系统输出的励磁电压。
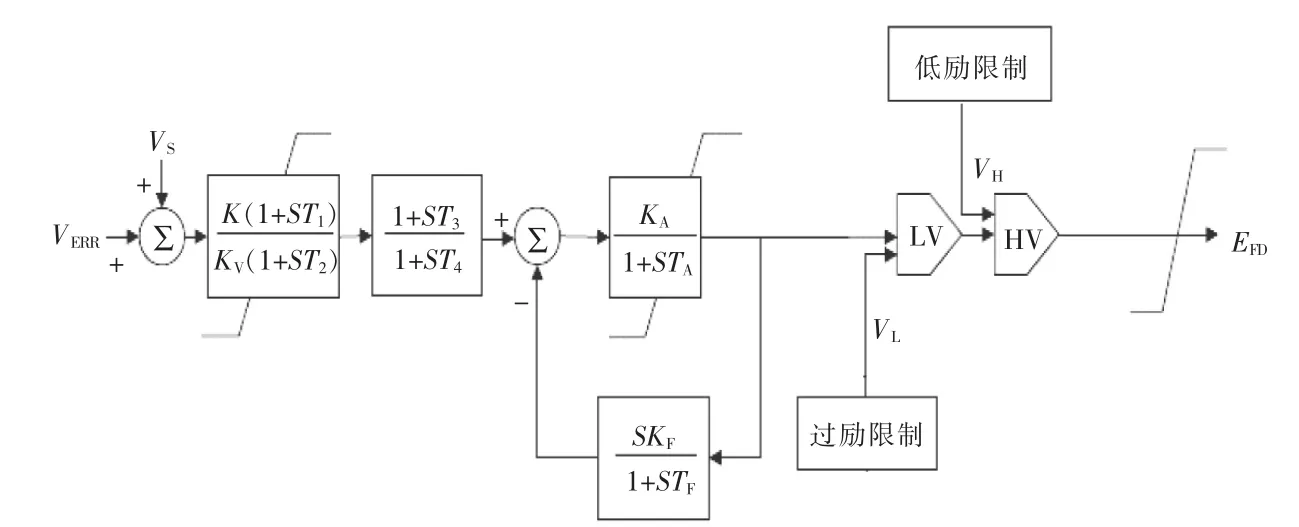
图2 自并励励磁系统模型Fig.2 Typical self-excitation excitation system model
在静态稳定、 暂态稳定和动态稳定的不同系统扰动场景下, 电力系统须要针对水电和火电进行协调调节,既能提供足够的励磁电压调节比例,又能够提供恰当的系统阻尼特性, 以保证在各场景均能够在较短的时间尺度内恢复稳定。
2 多机系统励磁模型
水电和火电机组励磁系统调节励磁电压的直接结果是改变发电机机端电压、机组间无功分配、发电机输出有功功率和整个电力系统的阻尼特性。 根据系统中所有参与励磁调节的自并励励磁系统产生的同步力矩和阻尼力矩间的协调, 可以在多种扰动场景下对系统的阻尼特性进行优化控制。
水火电协调的多机系统转子运动方程:
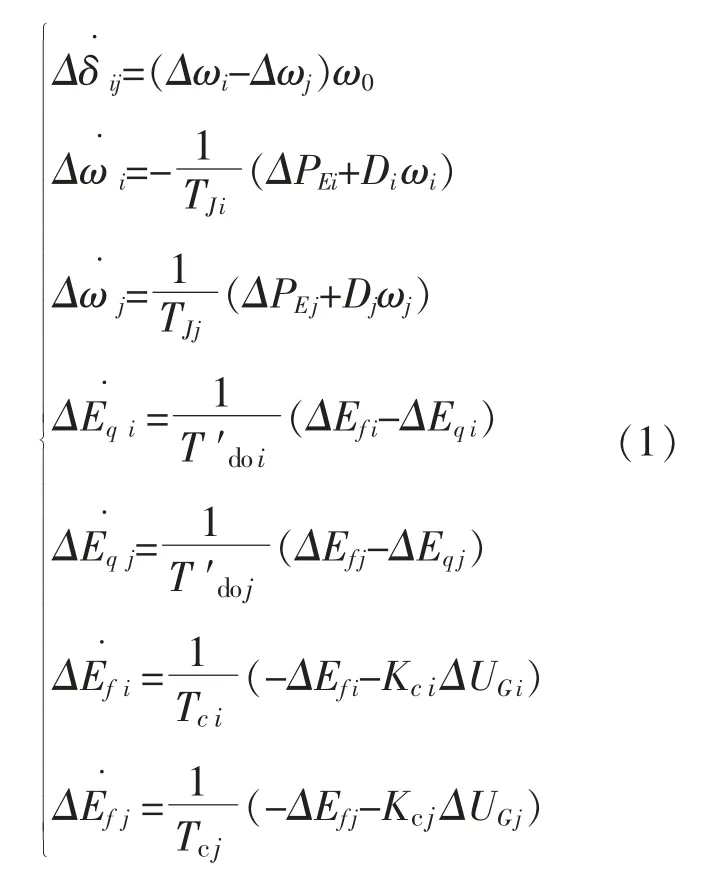
由式(1)可得多机系统状态方程为
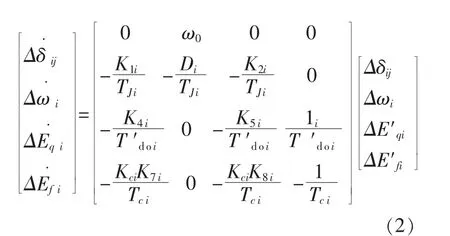
本文建立的水电火电多场景协调优化模型拓扑结构如图3 所示。 由图3 可见,在实际运行中,考虑不同运行状态下励磁电压和机端电压的限幅时,根据水电和火电励磁系统的不同参数特性,交互水电火电励磁系统间的控制信息,经过滤波、比例和移相环节后, 再与给定的参考电压和系统实时测量电压进行比较; 以整个电力系统中的所有水电和火电机组励磁电压、电网电压水平为基础,优化电力系统内能够参与励磁协调控制的机组的励磁参数, 得到系统在不同扰动和动态振荡场景下的最优阻尼参数。
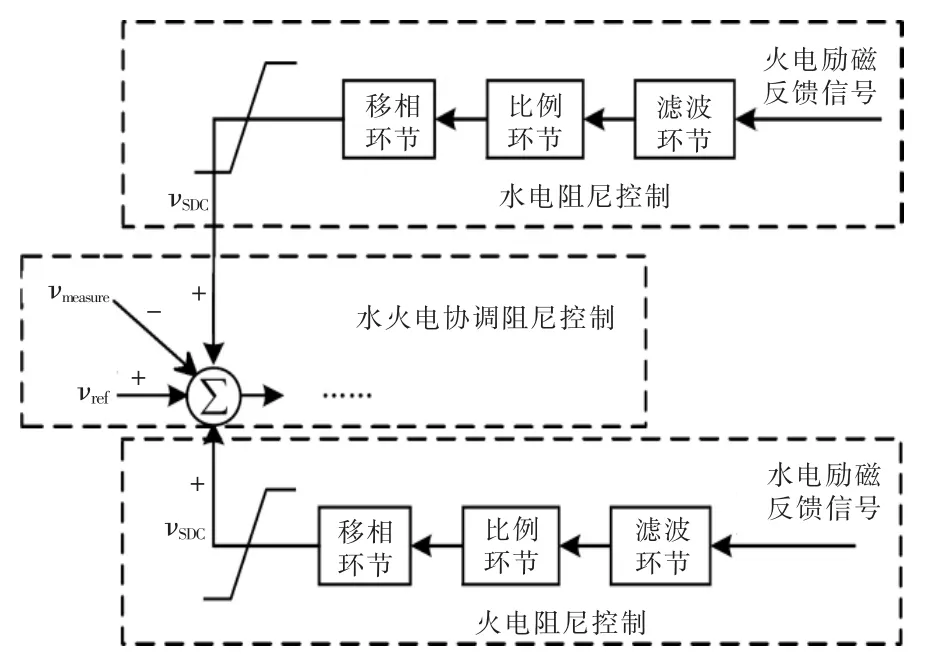
图3 水电火电多场景协调优化模型拓扑结构Fig.3 Topological structure of multi-scenario coordination optimization model for hydropower and thermal power
同步发电机(尤其是大型水力同步发电机)的励磁控制系统, 对电力系统的安全稳定运行具有重要的影响。励磁控制系统的作用很多,其主要作用是在可靠性高的前提下维持发电机或其他控制点的电压在给定值水平上, 提高电力系统运行的稳定性。下面分别从静态稳定、暂态稳定和动态稳定3 方面分析励磁系统的作用。
(1)静态稳定性
若发电机的空载电动势恒定, 则发电机的有功功率将随功率角变化, 通常将功率差与时间差的导数作为电力系统静态稳定的判据。 对于无自动励磁调节的发电机来说,在功率角<90°的情况下,系统是不稳定的,即稳定极限角为90°。 若发电机在运行中可自动调节励磁, 则此时空载电动势即为变化值。 当空载电动势的增加引发发电机定子电流增加,使发电机机端电压减小时,励磁调节装置将调节励磁电流,增加空载电动势,使发电机电压稳定在一定水平,实现了静态调节功能。
(2)暂态稳定性
当发电机受到大的扰动时, 能否继续保持同步运行,是暂态稳定研究的问题。 通常认为,提高励磁系统的强行励磁能力, 加大电压强励倍数及电压上升速度, 是提高电力系统暂态稳定性的最经济有效的手段之一。
(3)动态稳定性
动态稳定是指电力系统受到扰动后, 恢复至原始平衡点或过渡到新的平衡点过程的稳定性。可以将动态稳定性理解为电力系统机电振荡的阻尼问题。 当阻尼为正时,动态是稳定的;当阻尼为负时,动态是不稳定的;阻尼为零时,是临界状态。对于零阻尼或很小的正阻尼, 都是电力系统运行的不安全因素,应采取措施提高阻尼。励磁控制系统中的自动电压调节作用, 是造成电力系统机电振荡的阻尼变弱甚至变负的最重要原因之一。 在正常应用的范围内, 励磁电压调节器的负阻尼作用会随着开环增益的增大而加强。 提高电压调节精度的要求和提高动态稳定性的要求是矛盾的,须要平衡二者的关系。目前,大多采用电力系统稳定器(PSS)来提高电力系统的动态稳定性。
3 水火电协调多场景阻尼优化模型
3.1 阻尼优化控制模型
将电力系统中的小扰动、 大扰动和动态振荡视为水电、 火电协调励磁控制系统的稳定控制问题。在不同场景下,对励磁系统传递函数中K1t~Kct各参数所决定的状态方程进行线性化, 并根据电力系统运行状态中实时测量采集的数据进行离散化处理, 得到励磁系统阻尼优化控制的离散小信号模型,即可优化系统阻尼控制器的参数。
水火电协调的励磁控制系统可表示为一个离散非线性切换系统:
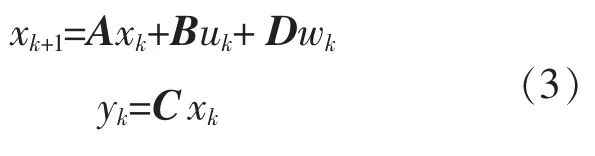
式中:A∈Rn×n,B∈Rn×m,C∈Rl×n,D∈Rn×r为离散线性水火电协调励磁控制系统动态矩阵;xk∈Rn为离散线性水火电协调励磁阻尼控制的电力系统运行状态数据;uk∈Rm为水火电协调励磁控制系统各控制参数输入向量;wk∈Rr为小扰动、大扰动和动态振荡条件下的多场景扰动输入向量;yk∈Rl为水火电协调励磁控制系统在最优阻尼控制目标下的阻尼参数输出。
定义励磁控制系统阻尼控制优化指标:
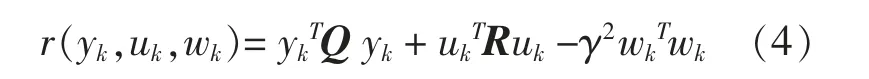
式中:Q,R 为水火电协调励磁控制系统参数初始值正定矩阵;γ 为给定的扰动修正系数,γ 的取值对应于小扰动、 大扰动和动态振荡等多场景下的扰动修正值;ykTQ yk为考虑电力系统运行状态测量误差下的水火电协调励磁控制系统输出变化量;ukTRuk为电力系统中各个参与阻尼控制的机组励磁系统对电力系统状态测量数据输入变化范围的约束值;γ2wkTwk为系统针对不同扰动场景下为了获得最优阻尼参数须进行的修正量。
根据不同扰动下的电力系统阻尼优化控制目的, 最优水火电协调励磁控制参数优化策略为使能量不平衡量指标最小。 将电力系统在特定扰动场景下的能量不平衡量作为在时域上的阻尼优化控制优化指标:
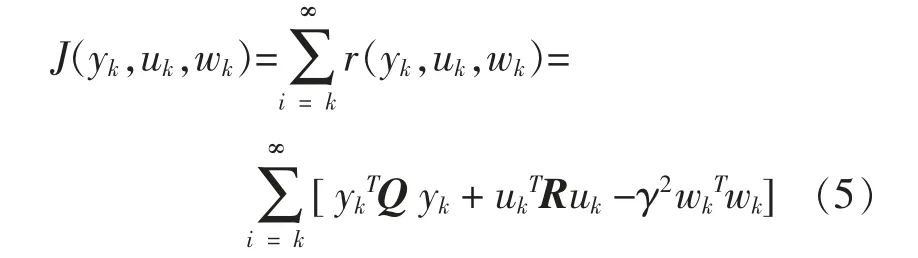
式中:uTk为水火电协调励磁控制系统各控制参数的最优解向量。
根据式(5)可知,电力系统扰动下的能量不平衡量指标,既与水电、火电协调励磁控制系统提供的阻尼特性有关, 也与扰动wk有关。 小扰动、 大扰动和动态振荡条件下的多场景扰动wk为不可控扰动量。考虑到多场景扰动对能量不平衡量指标影响,本文选取较为保守的阻尼优化控制策略,以保证在系统最严重扰动下的稳定。 因此,水火电协调的电力系统阻尼优化控制策略可描述为
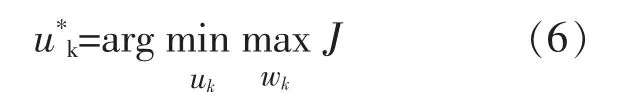
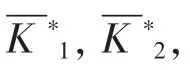

水火电协调励磁控制系统各控制参数的最优解向量u*k中, 最优解向量与u*i的关系为u*k=u*iTRu*i。
令:
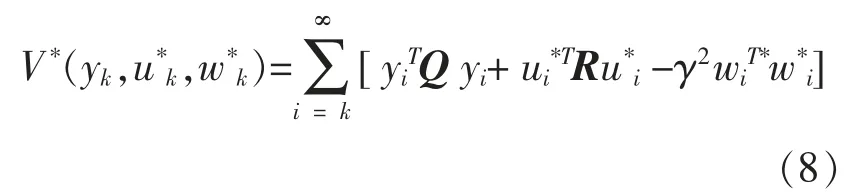
则有:
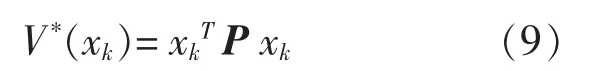
式(9)中矩阵P 满足:

由式(8)~(10)可得:

3.2 阻尼优化控制模型求解算法
在以上提出的多场景扰动阻尼优化控制模型基础上, 在水火电协调励磁控制系统模型拓扑结构已知的条件下, 通过电力系统运行状态数据反馈来求解阻尼优化控制的励磁系统控制参数最优解。 算法具体步骤如下。
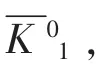
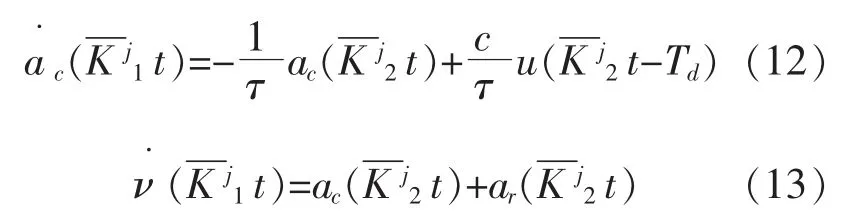
式中:t 为时间;ac(t)为水火电系统等值同步电源转子加速度;ar(t)为水火电系统功率控制拟获得的目标加速度;τ 为水火电系统总的惯性时间常数;Td为水火电系统功率控制系统的时延。
③更新P,矩阵P 的修正方程为
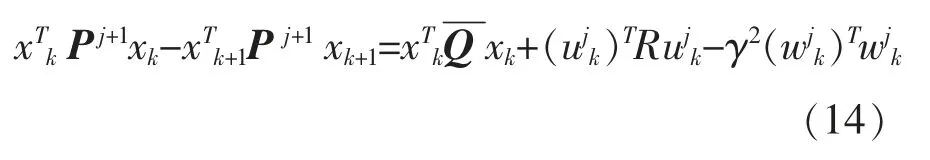

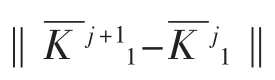
4 算例分析
4.1 单机无穷大示例
以实际电网中的某台发电机搭建如图4 所示的单机无穷大系统。发电机相关参数:惯性时间常数为11.15 s;直轴暂态开路时间常数为8.72。 系统的励磁参数: 自并励静止励磁系统的励磁稳态增益为377 p.u.; 等效励磁时间常数T1,T2 分别为0.3,0.06;暂态增益为75 p.u.。PSS2B 型PSS 为速度偏差与加速功率共同输入,初始增益为1.0 p.u.。
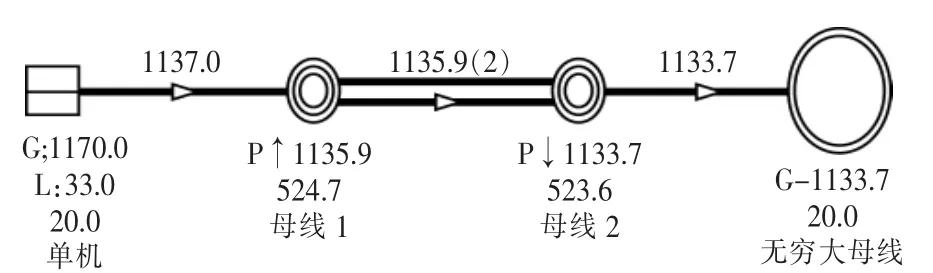
图4 单机无穷大系统Fig.4 Single machine infinity system
在母线1-母线2 线路三永N-1 故障下,系统存在动态稳定问题。 振荡频率0.747 Hz, 阻尼比为-0.0162。调整发电机出力后得系统静态稳定极限为1 850 MW,暂态稳定极限为1 235 MW,动态稳定极限为1100 MW。PSS2B 型PSS 的增益为临界增益的1/3~1/2。假设PSS 初始增益为1/3,则PSS 增益最多可由1.0 调至1.5, 系统动态稳定极限增至1 170 MW,与暂态稳定极限差值为65 MW。
由系统励磁参数及式(11)可知,励磁增益K的最小值为168 p.u.。 为继续提高系统输电能力,将励磁增益K 由377 p.u.降至352 p.u.,系统稳定极限变化示于表1。 由表1 可知,降低发电机励磁暂态增益, 系统暂态稳定极限下降至1 190 MW,而动态稳定极限提高至1 185 MW,动态稳定极限与暂态稳定极限基本持平, 整体输电能力较原始参数增加了8%,即85 MW。

表1 励磁增益对系统输送极限的影响Table 1 Effect of excitation gain on system delivery limit
图5 为输送功率1 100 MW 情况下, 发生母线1-母线2 三永N-1 故障的原参数、 调整PSS参数、调整PSS 与励磁参数时,故障另一回路有功功率变化的情况。 系统低频振荡现象得到了有效抑制,且无暂态稳定问题发生,验证了本文模型的有效性。
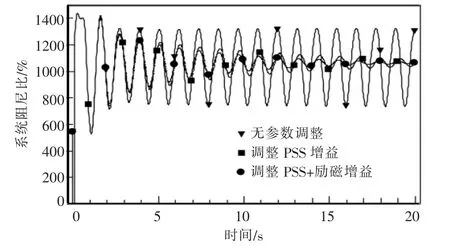
图5 励磁暂态增益对系统阻尼比的影响Fig.5 Effect of excitation transient gain on system damping ratio
4.2 华中电网算例
华中地区多大型水电,电网的动态稳定问题严重。 图6 为华中电网某年地理接线图,各省电网规模及联络线功率如图所示。 此方式为夏季、大负荷、水电大发的豫北-湖南对冲方式,湖南外送功率1 000 MW,豫北外送功率3 600 MW。
表2 为运行方式及部分小干扰分析结果。 由表2 可知,豫北-湖南振荡模式系统阻尼比最小,为主导振荡模式。
统计主导振荡模式的主要参与机组,满足条件的发电机共60 台,其中交轴暂态开路时间常数为0 的机组为水轮发电机。 发电机均为典型的自并励静止励磁系统,主导振荡模式部分参与机组如表3 所示。

图6 华中电网分区图Fig.6 Huazhong power grid zoning map

表2 初始运行方式部分小干扰分析表Table 2 Initial operation mode partial small interference analysis table

表3 豫北-湖南振荡模式湖南部分参与机组Table 3 Partial participation of the North-South Hunan oscillation mode

续表3
假设全部参与机组PSS 增益均满足整定要求,且为临界增益的1/3。 为提高系统动态稳定极限,将PSS 增益加大为原来的1.5 倍,即临界增益的1/2。经计算,PSS 调整后豫北断面动态稳定极限增至5 800 MW, 与暂态稳定极限7 250 MW 之差为1 450 MW。表3 中给出了主要参与机组的直轴暂态开路时间常数、 励磁稳态增益及励磁暂态增益。 将当前励磁稳态增益与最小励磁增益作为边界, 以可调励磁增益比例和延时环节时间常数为待优化参数, 运用本文提出的水火电协调励磁系统阻尼优化控制算法进行参数优化控制, 表4 为优化后部分参数结果。
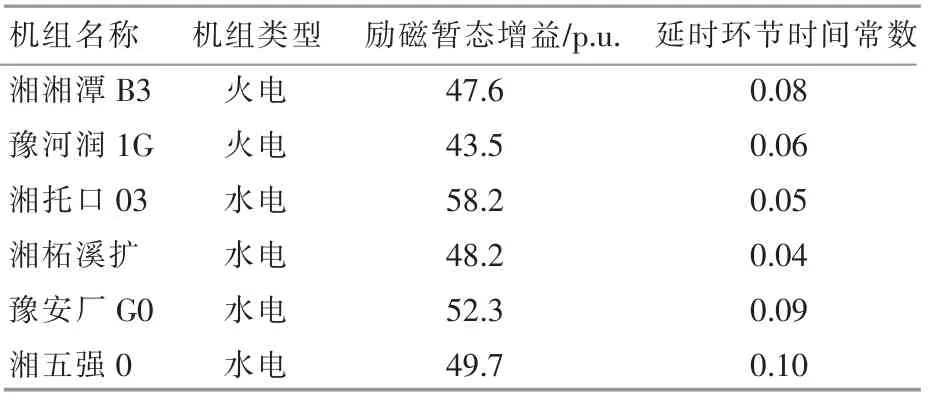
表4 部分励磁系统优化后参数Table 4 Parameter list after excitation system optimization
豫北断面动态稳定极限增至6 200 MW,与暂态稳定极限6 220 MW 基本相同, 输电能力与调整前相比增加了400 MW。 图7 为调整励磁前后,豫北外送5 800 MW 发生惠济-获嘉单永N-1 故障时,宋家坝-岗市线路有功功率曲线,系统动态稳定性有一定的提高,验证了本方法的有效性。

图7 励磁增益变化对宋家坝-岗市线路功率的影响Fig.7 Effect of excitation gain variation on line power of Songjiaba -Gang City
5 结语
针对水电高占比地区存在的动态稳定与暂态稳定等多场景稳定控制参数不协调问题, 本文提出了基于水火电协调的励磁参数协调优化方法。通过算例仿真得出以下结论。
①以系统多场景扰动下的能量不平衡量最小为目标函数,通过对系统参数的优化,能有效地协调系统的动态稳定性和暂态稳定性。
②水火电协调励磁系统的阻尼优化控制模型及其求解算法适用于励磁参数的优化。 励磁系统作为低频振荡的根源, 其参数的合理性可在PSS无调整裕度的情况下提高系统的整体输电能力。
③本文所提出的水火电协调阻尼控制方法,能够有效地协调电力系统中多场景扰动下的励磁系统控制, 有效提高水电占比较高的电力系统多场景稳定能力。
