基于可能性c 均值聚类和模糊评判的调峰负荷辨识
2020-12-16孙亚璐张中丹毕文瑾郑伟强查雯婷
孙亚璐, 张中丹, 陆 军,毕文瑾, 郑伟强, 查雯婷
(1.国网甘肃省电力公司 经济技术研究院, 甘肃 兰州 730050; 2.中国矿业大学(北京) 机电与信息工程学院,北京100083; 3.国网营口供电公司, 辽宁 营口 115000)
0 引言
可再生能源出力具有波动性及反调峰特性,大规模风电并网增加了系统调峰难度,导致弃电现象严重, 亟待寻找消纳可再生能源的有效方法。 现代柔性工业负荷(如电解铝、碳化硅、钢铁及水泥等)具有灵活的调控能力,且调控容量大,响应速度快,可用于消峰填谷等控制,从而促进风 电的消 纳[1]~[3]。
在进行负荷辨识前, 须根据不同的负荷特征,将综合负荷聚类。 文献[4]将负荷归纳出可调节特性和可中断特性,将一类高载能负荷进行了特性区别,便于后续负荷特征提取及聚类。 针对传统的模糊c 均值聚类方法不适于非正态分布数据集的聚类,且处理高维数据集收敛速度缓慢的问题[5],[6],文献[7],[8]分别提出了一种基于核的模糊c 均值逐层聚类方法和改进的模糊c 均值聚类方法。 针对模糊c 均值聚类算法须要人为确定聚类数目和模糊加权指数m。 文献[9]以聚类有效性判别指标为基础自动确定聚类数目,并通过模糊决策的方法确定最优的m 取值,但分配的隶属度缺乏合理性。
针对上述问题,本文首先将综合负荷分为连续/离散型调峰负荷和不可调峰负荷,提取不同负荷的特征参数。 以连续调节特征参数表示连续型调峰负荷跟踪可再生能源出力波动的能力, 以阶跃变化特征参数及调节间隔特征参数表示离散型调峰负荷的能力;其次根据特征参数,基于可能性c 均值聚类算法进行负荷聚类。 可能性c 均值聚类算法反映了数据点到聚类中心的真实距离,对消除噪声具有较好的鲁棒性, 有效地解决了模糊c 均值聚类算法对噪声和野值敏感的问题[10]~[12]。可能性c 均值聚类算法, 可有效降低不可调峰负荷被误划分为调峰负荷的概率; 再次计算特征参数对聚类中心的隶属度, 采用模糊评判方法辨识综合负荷中两类调峰负荷的占比; 最后通过算例验证方法的可行性和有效性。
1 调峰负荷特征参数提取
1.1 柔性工业负荷参与调峰的特性分析
柔性工业负荷具有一定的可调节能力, 通过提高用电功率来消纳风电,也可跟踪电源变化。它分为连续型和离散型调峰负荷。
(1)连续型调峰负荷的调节特性
连续型调峰负荷主要包括铁合金和碳化硅等负荷。连续型调峰负荷的爬坡率较小,但一次调节完成后不需要等待就可以进行下一次调节。 图1为典型铁合金负荷运行曲线。 该铁合金负荷的可连续调节范围为6.5%~101.8%, 响应调节时爬坡率可达到±8 MW/min。
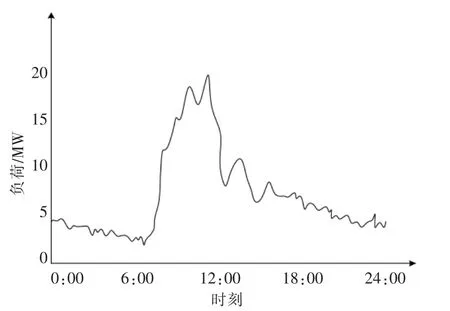
图1 典型铁合金负荷运行曲线Fig.1 Typical operational curve of a ferroalloy plant load
(2)离散型调峰负荷的调节特性
离散型调峰负荷主要包括电解铝等负荷。 电解铝在生产过程中,可调节范围为60%~105%,在此范围内调节不影响产品质量和设备安全,只影响产量。 离散型调峰负荷调节速度快,但每次调节结束后需要等待一定时间才能进行下一次调节。图2 为典型电解铝厂负荷运行曲线。该电解铝负荷在响应调节时的爬坡率可达到±50 MW/min,但其两次调节的时间间隔较长,为4 h 以上。
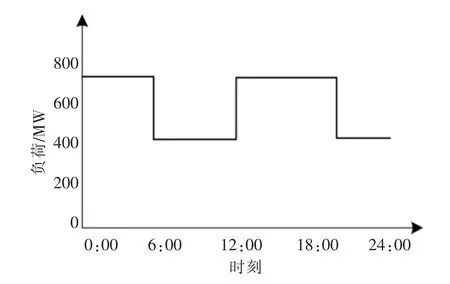
图2 典型电解铝厂负荷运行曲线Fig.2 Typical operational curve of an electrolytic aluminum load
1.2 提取连续调节特征参数
连续型调峰负荷基于调节指令响应改变自身用电功率,用电曲线可跟踪可再生能源出力波动曲线。 因此,将负荷用电曲线与可再生能源出力曲线变化趋势相关程度定义为连续调节特征参数,从而在综合负荷中提取连续型调峰负荷。
在相关程度的比较中,考虑负荷连续调节功率与可再生能源发电功率数量级相差较大引起的误差,首先进行数据标准化处理。 设X=[x0,x1,x2,…,xn]q(n+1),其中xi=[xi0,xi1,…,xiq-1]T, x0为可再生能源一天q 个点的日出力曲线,x1,x2, …,xn为n组综合负荷一天q 个点的日用电功率曲线,则:
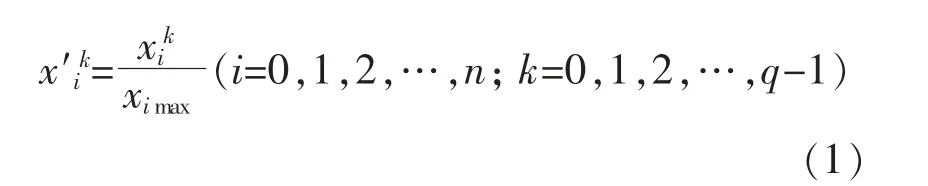
式中:标准值X′=[x′0,x′1,x′2,…,x′n]q(n+1);x′i=[x′i0,x′i1,x′i2,…,x′iq-1]T;ximax=max(xi0,xi1,xi2,…,xiq-1)。
采用负荷用电功率变化率与可再生能源发电变化率之间的距离的倒数Ji表示第i 组综合负荷的连续调节特征参数。Ji越大,连续型调峰负荷占比越大,负荷响应调节能力越强,其表达式为
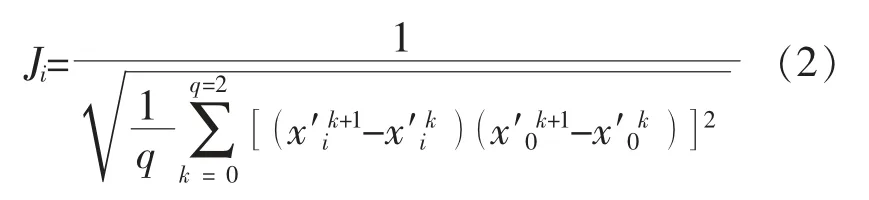
式中:x′0k为可再生能源发电出力曲线中的第k 个点标准化后的值;x′ik为负荷i 用电功率曲线中的第k 个点标准化后的值。
图3 为大规模风电接入时, 包含和不包含连续型调峰负荷的综合负荷特性曲线及可再生能源出力波动曲线。

图3 含连续型调峰负荷的综合负荷及风电波动曲线Fig.3 Output curve of wind power and synthetic load's characteristic curves with continuous load
由图3 可知, 包含连续型调峰负荷的综合负荷具有较好的跟踪风电出力的调节能力, 根据式(2)计算,图中连续调节特征参数为27.957 2。
1.3 提取阶跃变化特征参数及调节间隔特征参数
离散型调峰负荷与连续型调峰负荷的相似之处在于两者均能响应电源出力调节自身用电功率,而离散型调峰负荷在接受指令后,可以直接投切部分设备改变用电功率, 即负荷曲线会发生阶跃性变化。因此,定义阶跃变化特征参数表示负荷响应可再生能源发电出力时的负荷阶跃变化率,即:找到跟踪风电出力波动而阶跃变化的点,记为T={tk│x′0k<x′0,up或x′0k>x′0,down,0≤k<q-1},T 为可再生能源出力低于下设定值x′0,up或高于上设定值x′0,down的时刻tk的集合。 计算此时负荷的功率变化率, 取绝对值最大值记为第i 组综合负荷的阶跃变化特征参数Δxi,即:
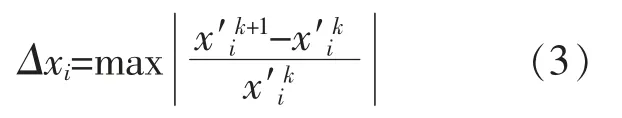
离散型调峰负荷每次调节结束后需要等待一定时间才能进行下一次调节, 因此将响应调节的间隔时间定义为调节间隔特征参数。 将相邻的阶跃变化特征参数超过阈值的时刻点为起始点,计算相邻两阶跃变化点之间的间隔时间, 取最大值为第i 组综合负荷的调节间隔特征参数Δti,若负荷无阶跃变化,则调节间隔特征参数取0,即:
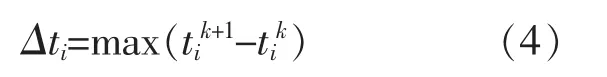
图4 为大规模风电接入时, 包含和不包含离散型调峰负荷的综合负荷特性曲线及可再生能源出力波动曲线。

图4 含离散型调峰负荷的综合负荷以及风电波动曲线Fig.4 Output curve of wind power and synthetic load's characteristic curves with discrete load
由图4 可知, 包含离散型调峰负荷的综合负荷具有较好的跟踪风电出力调节用电功率的能力。 根据式(3)和(4),计算图中阶跃变化特征参数和调节间隔特征参数分别为0.304 2 和0.246 9。
利用这3 个参数进行负荷聚类, 不仅可以提取出跟踪可再生能源出力波动特性的两类调峰负荷,而且特征参数个数少、计算速度快。
2 基于可能性c 均值聚类和模糊评判的连续/离散型调峰负荷辨识
基于上述特征参数, 采用可能性c 均值聚类算法求解连续/离散型调峰负荷和不可调峰负荷的聚类中心,从而将综合负荷分为3 类。然后根据聚类结果,采用模糊评判方法计算连续/离散型调峰负荷在综合负荷中的占比, 实现调峰负荷的有效辨识。
2.1 基于可能性c 均值的调峰负荷聚类
可能性c 均值聚类算法在模糊c 均值聚类算法基础上,放松了隶属度约束条件,令Y=[y1,y2,…yn] 为给定的样本集合;s 为样本空间的维数;n为样本个数(即n 组综合负荷);c 为对Y 进行划分的聚类个数。 可能性c 均值聚类模型为
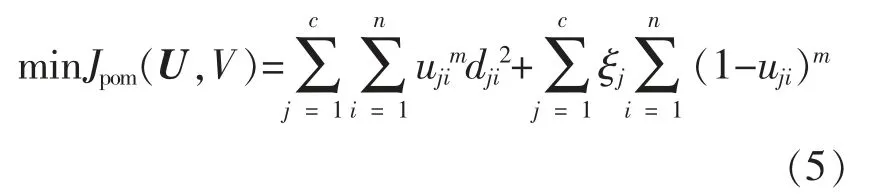
式中: m 为模糊系数,m>1; U 为可能性划分矩阵,U=[uji]c×n;uji为第i 个数据属于第j 类的可能性;V 为由c 个聚类中心向量构成的s×c 型矩阵,V=[ν1,ν2, …,νc];dji为从样本点yi到中心νj的距离,本文采用欧氏距离,dji=‖yi-νj‖;ξj为用户定义的参数,取值为
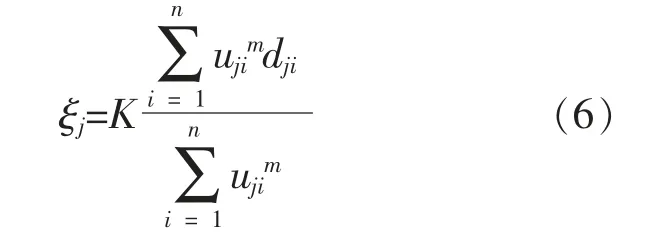
式中:K>0,通常取值为1。
目标函数的第一项与模糊c 均值聚类算法相同,体现了不同数据点到各类中心的加权距离;第二项是惩罚项,用来避免可能性矩阵为0 的情况。可能性c 均值聚类算法迭代公式为
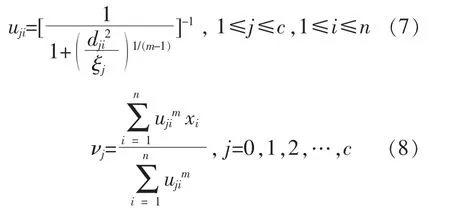
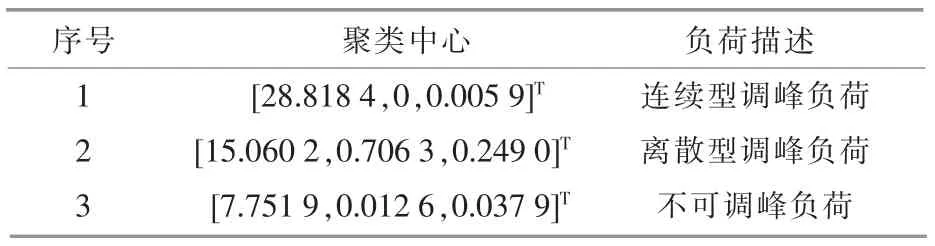
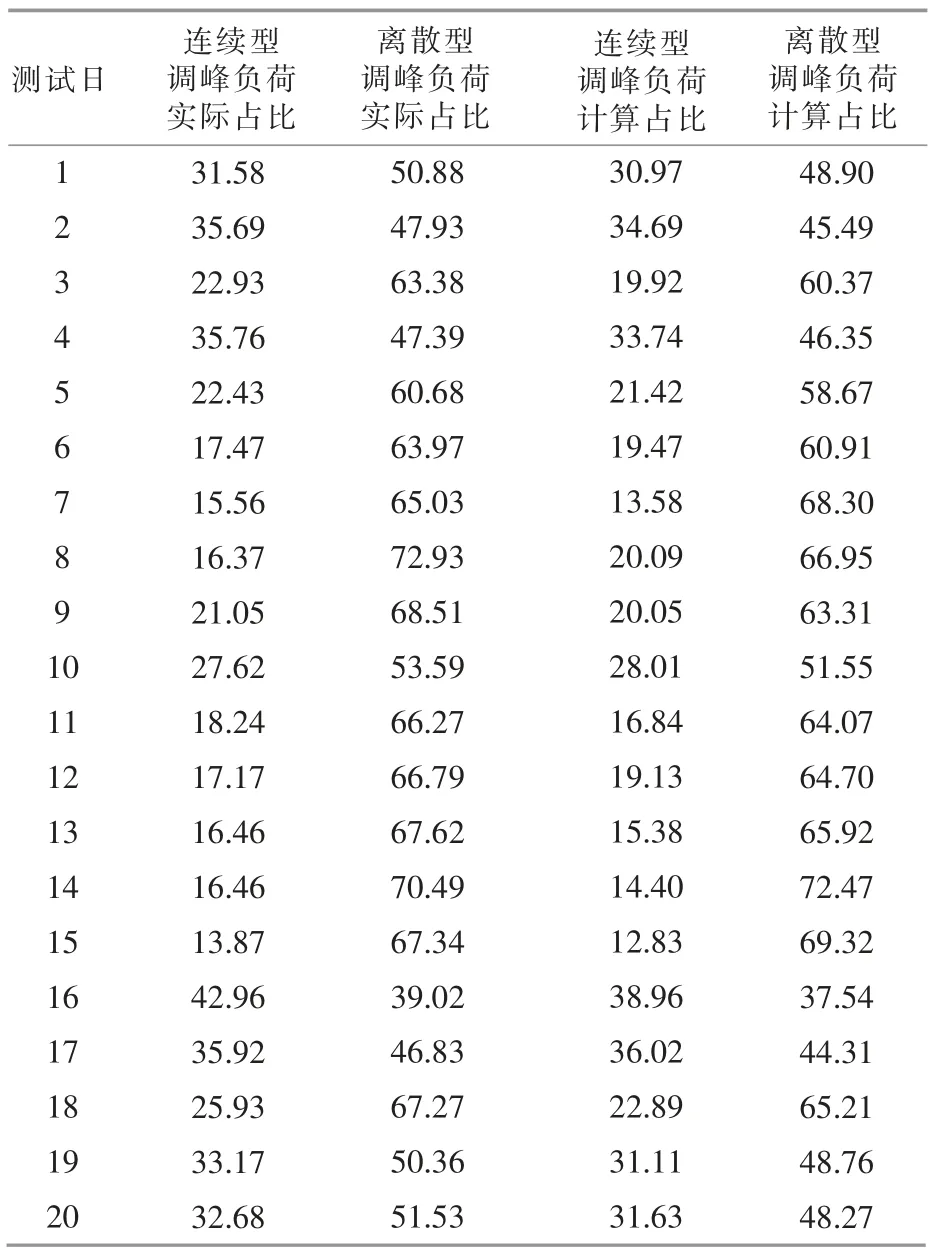
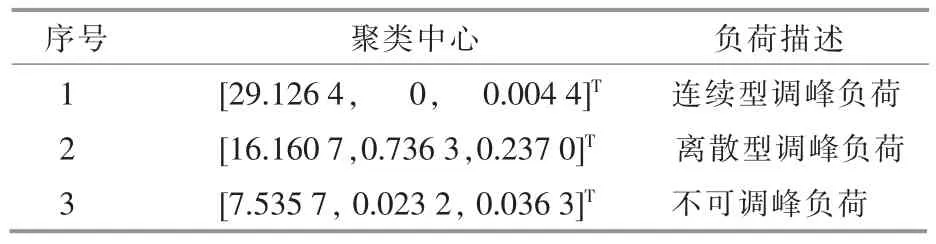
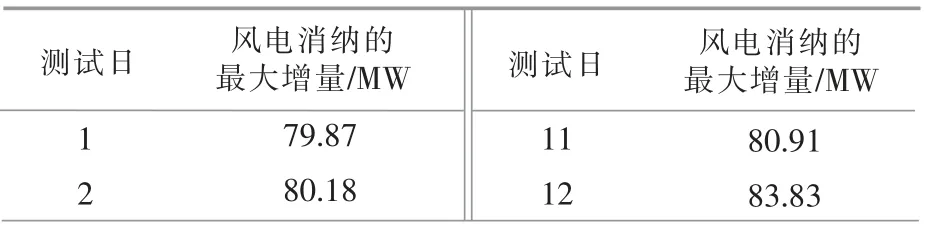
由式(7)可以看出,可能性c 均值聚类算法中距离dji>djn,等价于uji 基于可能性c 均值聚类算法的3 类负荷聚类方法步骤如下。 ①采集n 天的变电站综合负荷曲线、 可再生能源出力曲线作为原始样本。 ②采用式(1)对原始样本数据进行标准化。采用式(2)~(4)计算原始样本特征参数,构成样本特征参数向量yi=[ji,Δxi,Δti]T,j=(1,2,…,n)。 ③设置分类数为c=3, 初始化各类中心V0=[ν10,ν20,ν30]3×3; 设置模糊系数m 及收敛精度ε,以及初始化迭代次数f=0 。 ④用式(6)计算ξj,带入式(7)计算Uf+1。 ⑤用式(8)计算Vf+1,令f=f+1。 ⑥重复步骤④,⑤,直到满足终止条件: 从而得到聚类中心V=[ν1,ν2,ν3]3×3。 基于模糊评判的调峰负荷占比辨识步骤如下。 ①对于第i 个样本,连续、离散型调峰负荷和不可调峰负荷的综合评价比例向量为pi=[pi1,pi2,pi3],其特征参数对各聚类中心的隶属度构成的隶属度向量为gi=[gi1,gi2,gi3], 其中gij为样本i 的特征参数向量yi属于第j 个聚类中心的隶属度,其表达式为 ②根据上述负荷的特征参数ji,Δxi,Δti, 对应出典型连续/离散型调峰负荷和不可调峰负荷的特征参数矩阵为Ytypicd=[Jtypicd,Δxtypicd,ttypicd]T3×3, 应用式 (10) 计算出其对各聚类中心的隶属度矩阵Gtypicd=[gtypicd,gtypicd,gtypicd]3×3,Gtypicd即 为pi到gi的 映射;G-1typicd即为反映射。 ③样本i 中3 类负荷的综合评判比例向量为 由式(11)可得3 类负荷在样本i 中的占比为 式中:Σp=pi1+pi2+pi3。 本文以甘肃电网某110 kV 变电站为例,对本文所提方法进行验证。该变电站包含17 条负荷馈线,含碳化硅、电解铝负荷和民用负荷3 种负荷,接入此变电站的4 个电厂中包含1 个装机容量为300 MW 的风电厂。 选取该变电站20 d 的负荷数据和接入该变电站的风电厂出力数据作为原始样本。 按照式(2),(3)计算各组数据的特征参数Y,如表1 所示。 表1 特征参数Table 1 Characteristics parameters 聚类数c=3,计算各类的聚类中心,结果如表2 所示。 表2 聚类中心Table 2 Cluster centers 表3 调峰负荷的实际占比与计算占比Table 3 Load's calculation proportion and real proportion% 采用均方误差计算, 本文所提方法各类负荷占比的误差ω 为 计算得到, 连续型调峰负荷占比误差为0.45%,离散型调峰负荷占比误差为0.63%。 误差均小于1%,表明本文所提方法的可行性。 为证明本文提出的基于可能性c 均值聚类算法比传统的模糊c 均值聚类算法更能精确的辨识调峰负荷, 对上述算例采用模糊c 均值聚类算法进行聚类后再求占比,特征参数保持不变,聚类中心如表4 所示。 表4 聚类中心Table 4 Cluster centers 得到各类负荷聚类中心后, 仍采用2.2 节的方法求各类负荷在综合负荷中的计算占比, 如表5 所示。 根据式(13)计算得到连续型调峰负荷占比误差为1.2%,离散型调峰负荷占比误差为1.4%。 采用模糊c 均值聚类算法的误差为可能性c 均值聚类算法的两倍以上。因此,本文采用的基于可能性c 均值聚类的调峰负荷辨识方法更有效。 在风电受阻时期, 可通过上调调峰负荷的用电计划,达到增加风电消纳的目的。 按照负荷总量为1 000 MW,调峰上调幅度为10%,调峰同时率为1,计算风电消纳的最大增量,如表6 所示。 表6 风电消纳的最大增量Table 6 Maximum increment of wind energy dissipation 续表6 本文针对大规模可再生能源接入电网后系统调峰困难的现状, 提出了一种基于可能性c 均值聚类算法和模糊综合评判方法的调峰负荷辨识方法。通过对调峰负荷特性进行分析,得到反映连续型和离散型调峰负荷的特征参数。 利用不同负荷特征参数, 基于可能性c 均值聚类算法对综合负荷进行聚类,得到连续/离散型调峰负荷和不可调峰负荷的聚类中心。在此基础上,制定不同负荷特征参数对聚类中心的隶属度, 基于模糊评判方法辨识综合负荷中连续/离散型调峰负荷的占比,为负荷参与调峰提供依据。最后,算例验证了所提方法的可行性和有效性。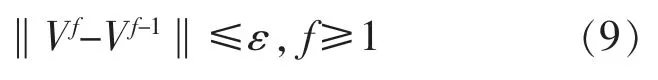
2.2 基于模糊评判的调峰负荷占比辨识

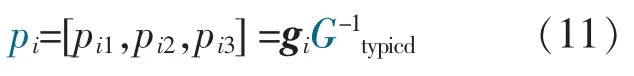
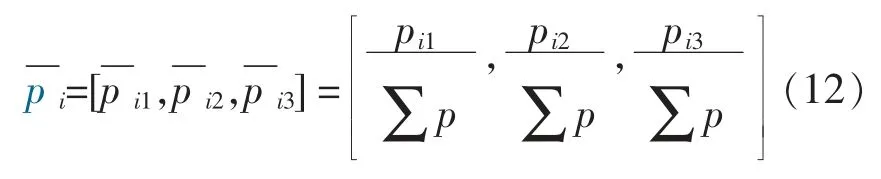
3 算例分析
3.1 方法的可行性


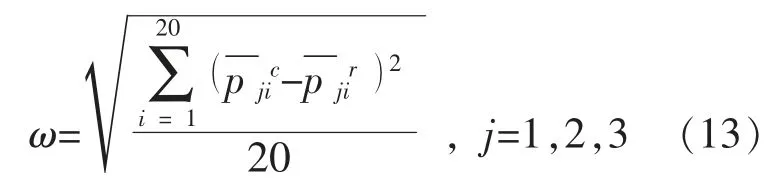
3.2 方法的有效性

4 结语
