基于单粒子寻优算法的铺层装备支架梁结构优化设计

2020-12-16李金亮王景华张磊安

可再生能源 2020年12期

王侃，李金亮，王景华，张磊安

（1.中海油（天津）管道工程技术有限公司，天津 300452； 2.淄博职业学院机电工程学院，山东淄博 255000；3.山东理工大学机械工程学院，山东淄博 255049）

0 引言

随着风电装机需求的不断提高，作为风电动力源的叶片，其结构设计至关重要。风电叶片内部为空芯结构，为保持叶片工作时能够平稳运行，内部通过主梁支撑，而主梁的制作通过在模具上铺放若干层玻璃纤维布来完成。目前的铺层工艺，完全采用人工，精度和效率低下[1]～[3]，据此开发了一套面向风电叶片玻璃纤维布铺放的专用装备。工程应用发现支架梁作为铺层装备的核心部件，其结构设计直接影响着叶片生产质量。因此，在考虑对其材料进行加强的同时，应对其结构参数进行优化，以提高其结构性能。

在优化方法的研究上，Alexandrem Nana[4]使用遗传算法成功对支架结构进行了结构优化。Abbasnia Reza[5]使用粒子群优化方法对机械结构进行了参数优化。刘显为[6]使用粒子群算法对叶轮结构进行了结构优化。王仲林[7]基于模态法对叶片结构进行分析计算，并据此进行结构优化以提高叶片结构的动态性能。赵丹阳[8]采用基于有限元的结构优化方法对装备进行优化重建。在结构优化方面，虽然粒子群算法与遗传算法寻优结果精确，但其计算次数随迭代次数增加而不断增大，在多数量计算中不具备优势[9]。

鉴于此，本文改进粒子群算法，提出一种寻优效率极高的单粒子寻优算法，结合装备的数学模型进行双参数迭代优化，既解决了铺层装备承载结构的应力不分散及材料冗余现象，又提高了结构可靠性。

1 算法设计

1.1 单粒子寻优算法

针对支架梁的双参数优化计算，本文提出一种类似粒子群算法的单粒子寻优算法，粒子群算法与单粒子寻优算法的对比如图1 所示。图1（b）中的单粒子寻优算法将寻优粒子下降到一个，减少了迭代计算的次数。

图1 粒子群算法与单粒子寻优算法的对比Fig.1 Comparison of particle swarm optimization and singleparticle optimization

借鉴粒子群算法，寻优粒子首先选中一个方向随机数α（α∈[0°，360°]），初始步长w0在坐标活动范围值的0.05～0.1 倍之间选取，步长wt在寻优中不断变化，设定寻优方向单位矩阵Dp。

粒子的移动矢量Xp可由初始化设定的wt与移动方向决定。

因此，粒子的位置迭代方程表示为

式中：P 为粒子的位置矩阵；0P 为粒子的初始位置矩阵。

同时，为准确移动至目标区域，须对寻优方向进行判断。图2 所示为寻优方向的选取，粒子随机选取方向为α（α∈0～360°）。

图2 单粒子算法寻优方向选择Fig.2 Choose of single-particle algorithms optimization direction

若初始α 为1 方向，则将1 方向初始点划定与1 方向垂直的边界，在限定方向（α-90 °，α+90°）外选取；若随机方向为2 方向，则以粒子初始点划定垂直于2 方向的边界，二次限定寻优方向；而后进入3 方向的选取，3 方向区域为最优选取方向。综上，方向选取的3 种情况为1-2-3，1-3，3。以上方向选取法则可表示为

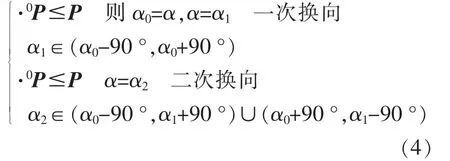
如因步长太长而在进行3 方向寻优后未找到目标值，则对wt进行下式中的赋值。

式中：mP 为中段粒子位置矩阵。

为避免粒子大幅移动，错过最佳位置，粒子的移动步长采用中段判断法，即中段位置优于初始点与终点。步长改变的同时，若此次寻优值优于先前值，则P 按式（3）进行赋值；否则，当前最佳位置P 赋值为mP。单粒子寻优算法以wt或迭代次数n 作为结束条件，随步长的减半及迭代运算的增加，程序根据wt及n 判断优化是否结束。

1.2 机构介绍及承载梁结构优化建模

根据铺层技术要求，本文设计了铺层装备模型（图3）。图3 中：地轨与承载结构采用滚轮导轨传动，两者的相对运动保证了放料装置的纵向（x方向）运动；横梁小车沿承载结构内置的导轨运动，通过齿轮齿条传动控制放料装置的横向（y 方向）运动；横梁小车与吊臂借助双丝杠相连接并沿z 轴方向传动；放料装置与吊臂通过双齿轮啮合沿y 轴方向转动。4 自由度放料装置可进行x，y，z轴的移动及绕y 轴方向的旋转，保证玻璃纤维布沿斜面的精准铺放。

图3 风电叶片玻璃纤维布铺层装备设计模型Fig.3 Design model of glass fiber fabric laying equipment for wind turbine blade

支架梁为对称机构，因避障需要，承载梁下支撑有两处折弯。 x 为下支撑上半部分高度，θ 为下支撑外翻角度，即下支撑与竖直面的夹角。实际运行中，支架梁承受自重及吊臂引起的集中载荷，须对其结构进行优化，使应力尽可能分散。以x，θ 为优化参数，对其进行结构建模，目标函数f（x，θ）为支架梁的应力分散程度，分散程度以数值高低表示，见式（6）。在约束范围内，进行优化使目标函数达到最大。

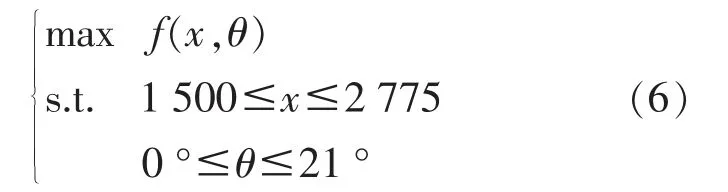
式（6）中，两参数范围较大将严重影响寻优效率，角度值与高度值的比值接近60。为方便计算，将式（6）中的角度值范围以100∶1 放大进行寻优，而在实际运算中将寻优值按1∶100 缩小，即步长在角度值层面缩小至w0的0.01 倍，以保证计算的准确性。

2 结构优化

根据计算，设置迭代的结束条件为

设置寻优范围的横向坐标为x，纵向坐标为θ，优化流程见图4。在初始化完成后，基于单粒子寻优算法对承载梁的最优值进行选取。

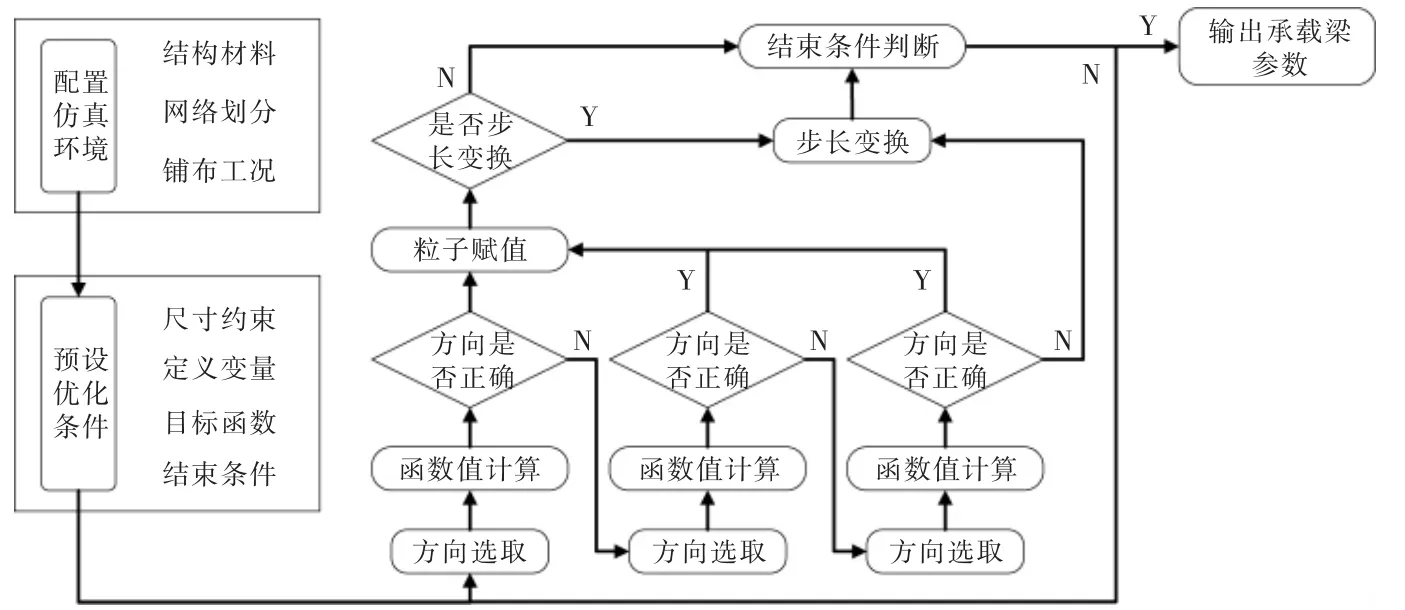
图4 迭代优化过程流程图Fig.4 Flow-process diagram of iterative optimization

单粒子寻优经48 次数值迭代后结束，输出两参数的变化如图5 所示。由图5 可知，x 的幅度变化相对较大，经过24 次迭代后，两参数数值趋于平稳。在wt到达0.048 8 后，退出寻优过程，最优结果为（2 369.704，10.108）。

图5 参数数值变化阶梯图Fig.5 Step diagram of parameter numerical variation

为了验证单粒子寻优算法的有效性及高效性，根据文献[10]和[11]，使用粒子群算法对支架梁进行了结构参数优化。设置粒子个数为10，经过多次迭代，计算结果如表1 所示。相比于粒子群优化算法的平均步数，单粒子寻优的计算效率提高了267%，且计算结果相近。

表1 粒子群算法寻优结果Table 1 Results of particle swarm optimization algorithm

3 试验及仿真验证

3.1 拓扑计算

为对支架梁优化结果进行验证，使用仿真优化计算软件Simright 对优化前后的结构进行结构拓扑验证，得到的模拟结果如图6 所示。图6 中，拓扑变量百分数表示结构应力强度的分布，数值越小说明此处材料越不能发挥其承载能力，数值为0 处的材料相当于闲置。隐藏应力数值低于10%的材料，并在右侧展示，做优化前后的应力数值效果比较。图6（a）中，支架梁应力集中现象明显，且存在大量的材料闲置；图6（b）中，相比于图6（a）的优化结果，集中应力得到了分散，材料闲置区域减小，结构性能得到了较好地发挥。拓扑模拟结果证明了此次优化的有效性。

图6 支架梁的拓扑数值分布Fig.6 Distribution of topological variables of support beam

3.2 现场铺布测试

使用优化参数制造的风电叶片玻璃纤维布铺层装备试验现场如图7 所示，据此对优化后的支架梁进行铺层试验验证。整个装备（涂装完成）重7 432.3 kg，上梁与支架采用螺栓连接，其余连接选用焊接。

图7 支架梁试验现场Fig.7 Field test of support beam

使用该装置进行铺层试验，模具长度为60 m，玻璃纤维布宽为1.2 m。取模具中段21～23 m进行检测，模具样本长度为2 m。使用此模具进行铺层后的玻璃纤维布表面数据如图8 所示。

图8 实测玻璃纤维布表面数据Fig.8 Measured surface data of glass fiber fabric

图8 中，铺层表面基本呈对称趋势。整体高0.15 m，沿y 轴方向呈现先下降后上升的趋势。选取x 计数点（数值为4）处的截面数据，进行模具与实际铺层表面的误差分析，分析结果如图9 所示。由图9 可知，本次试验中模具表面截面与铺层后玻璃纤维布表面截面的数值及其两者的差值，最大铺层误差为2.84 mm，位于支架梁中间部位对应图9 中铺层数据y 轴的0.6 m 处。实际运行中，支架梁中部承载部件较少，在承受吊臂及放料装置重量后，产生的变形较大。测试中得到的支架梁铺层数据虽有误差值，但铺层误差数值微小，对叶片的典型铺层生产不会造成影响，在工艺误差技术要求允许范围内，符合设计的要求。