某小口径枪弹弹头挤进过程数值仿真与分析
2020-12-16周克栋
唐 欣,周克栋,陆 野,沈 超
(南京理工大学 机械工程学院, 南京 210094)
弹头挤进是一个十分复杂的力学过程,随着计算机技术的迅速发展,越来越多的数值模拟方法运用于弹头挤进研究。Balla[1]以SPH77型152 mm榴弹炮和T72型125 mm坦克炮为研究对象,得到了挤进过程中变形、应力及相互作用结果。Deng等[2-3]运用非线性有限元方法分别对5.56 mm和9 mm枪弹弹头挤进及沿膛运动进行了数值仿真。
仿真计算过程中网格划分的数量和精度直接影响有限元计算的精度和效率,众多学者针对网格密度对仿真的影响进行了大量研究。邓记松[4]针对筒体开孔接管应力强度计算,分析了不同单元类型、单元技术和网格密度对计算结果精确性的影响。阎文兵[5]针对柴油机前托架模态分析,分析了不同网格密度对有限元分析的影响。但是针对挤进过程仿真时网格密度的影响却少有研究。
为研究身管内膛结构变化对挤进过程的影响,陆野[6]在满足设计要求的条件下改变坡膛角度,得到了坡膛受力条件最优的坡膛角度。闫利斌[7]建立了30 mm口径无膛线燃烧轻气炮弹丸弹裙挤进身管坡膛的有限元模型,分析弹裙高度对弹丸速度的影响。蒋泽一[8]对5.8 mm弹头挤进身管的过程进行了数值模拟,研究了坡膛长度变化对挤进过程的影响。但针对身管制造过程中的误差对弹头挤进的影响研究较少。
本文针对网格密度对弹头挤进过程中的挤进阻力、应力等参数影响开展了研究,并在此基础上分析阳线直径对弹头挤进过程的影响规律。
1 弹头挤进有限元模型
本文以某小口径枪弹弹头动态挤进过程为研究对象,弹头与身管三维模型如图1所示,采用前处理软件HyperMesh对身管、被甲、铅套、钢心进行网格划分。力边界条件为施加在弹头底部的火药气体压力随时间的变化曲线,该压力曲线是基于改进的内弹道模型编程求解获得的,是一个动态载荷,由于所分析的身管为实际身管的一部分,该部分身管在枪上的固定形式为完全固定,因此位移边界条件为施加在身管两端面的固定约束,采用自动接触算法,防止弹头挤进仿真过程出现网格畸变,计算过程中采用ALE自适应网格技术,确保计算的精度及效率。
身管材料采用30SiMn2MoVA,被甲材料为铜,弹头内部由铅套包裹着钢心,材料性能参数如表1所示。
由于弹头和身管材料在挤进坡膛的过程中出现了高应变率、材料温度升高、应力软化等一系列复杂的非线性力学形态,有限元仿真材料均采用Johnson-Cook材料本构模型[9-10],表达式为:
(1)
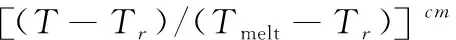
(2)
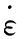
材料有塑性变形时,以等效塑性临界应变εr作为损伤的判活依据:
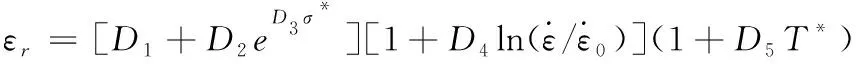
(3)
式中:D1~D5为材料断裂失效参数;σ*为应力三轴度。
采用线性损伤演化规律[10]描述材料刚度下降,材料累积损伤参数为
(4)
式中:D为材料内单元的损伤值,当单元损伤值D=1时,单元失效失去承载能力并从仿真中删除;Δε为等效塑性应变变化量。
2 网格密度对有限元仿真的影响
2.1 仿真研究方案
有限元分析方法的核心思想就是分块近似,因此网格密度或者结构的离散化的程度对计算的精度有很大的影响[11]。本文研究的是弹头挤进身管的动态过程,采用增加单元网格数量的方式来提高有限元仿真的计算精度。弹头在挤进的过程中主要与身管的阳线部分接触,坡膛阳线处网格划分复杂,坡膛阳线在接近线膛处结构尺寸最大,按照网格划分规则此处网格尺寸也最大,因此采用坡膛阳线上最靠近线膛位置的单个网格3个方向上最大的尺寸作为衡量坡膛处网格密度的标准。为研究不同网格密度对弹头挤进的影响,制定了5种方案。第1种方案最接近线膛处坡膛阳线单元网格最大尺寸为0.138 70 mm,第2种方案为0.075 64 mm,第3种为0.050 23 mm,第4种为0.033 28 mm,第5种为0.017 76 mm。不同方案对应的网格数量不同,具体的每种方案对应的网格划分情况如表2所示。为排除计算机平台对计算结果的差异性,本次有限元仿真的计算平台采用基于Windows 10安装的ANSYS 14.5软件,计算机处理器为Intel Core i7-8550U,分配给ANSYS软件的内存为8.00 GB,CPU核心数为2核。
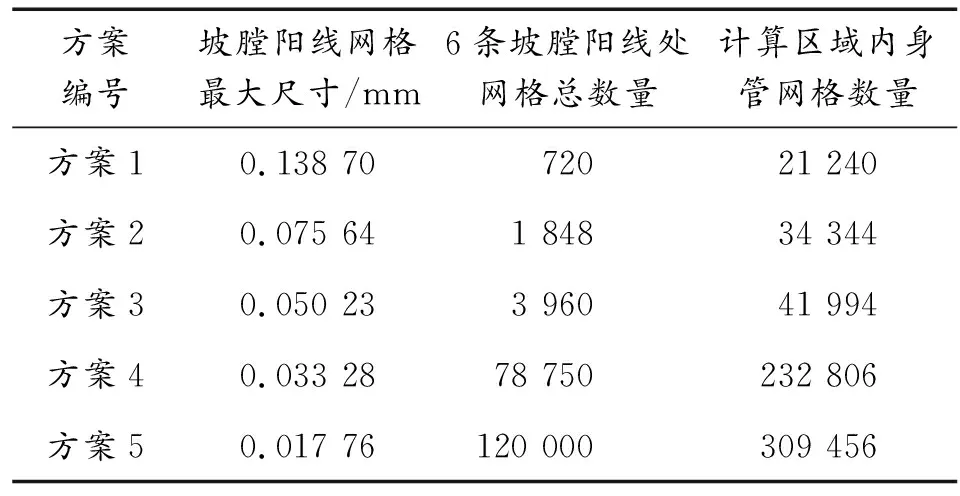
表2 网格划分方案
2.2 网格密度对坡膛处应力的影响
弹头在挤进的过程中受到坡膛导转侧的挤压作用而开始旋转,因此对于坡膛而言,导转侧的工作环境相较于非导转侧也更加恶劣,因此需要对导转侧进行应力分析,弹头在挤进的过程中主要与身管的阳线部分接触,对于右旋膛线,导转侧应力分析的研究对象选取坡膛五锥小端导转侧顶部特征点1,特征点位置如图2所示。
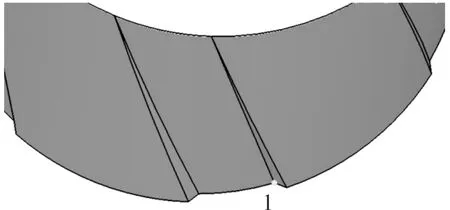
图2 身管坡膛处特征点位置示意图
分别对5种方案的不同网格密度的有限元模型进行仿真分析,获取5种方案下导转侧特征点1的应力随时间变化曲线如图3。
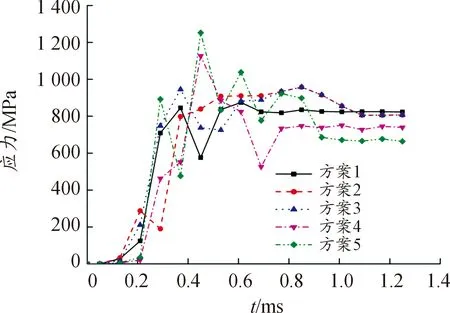
图3 特征点1五种方案的应力曲线
由图3的曲线对比可以看出,5种网格密度条件下特征点1的应力随时间变化规律是一致的,但不同网格密度的应力增大的速度和应力峰值有一定差异。方案1计算得到的应力峰值为874.4 MPa,方案2为957.8 MPa,方案3为 957.4 MPa,方案4为1 126.9 MPa,方案5为1 252.5 MPa,不同坡膛阳线网格数量应力峰值如图4所示。
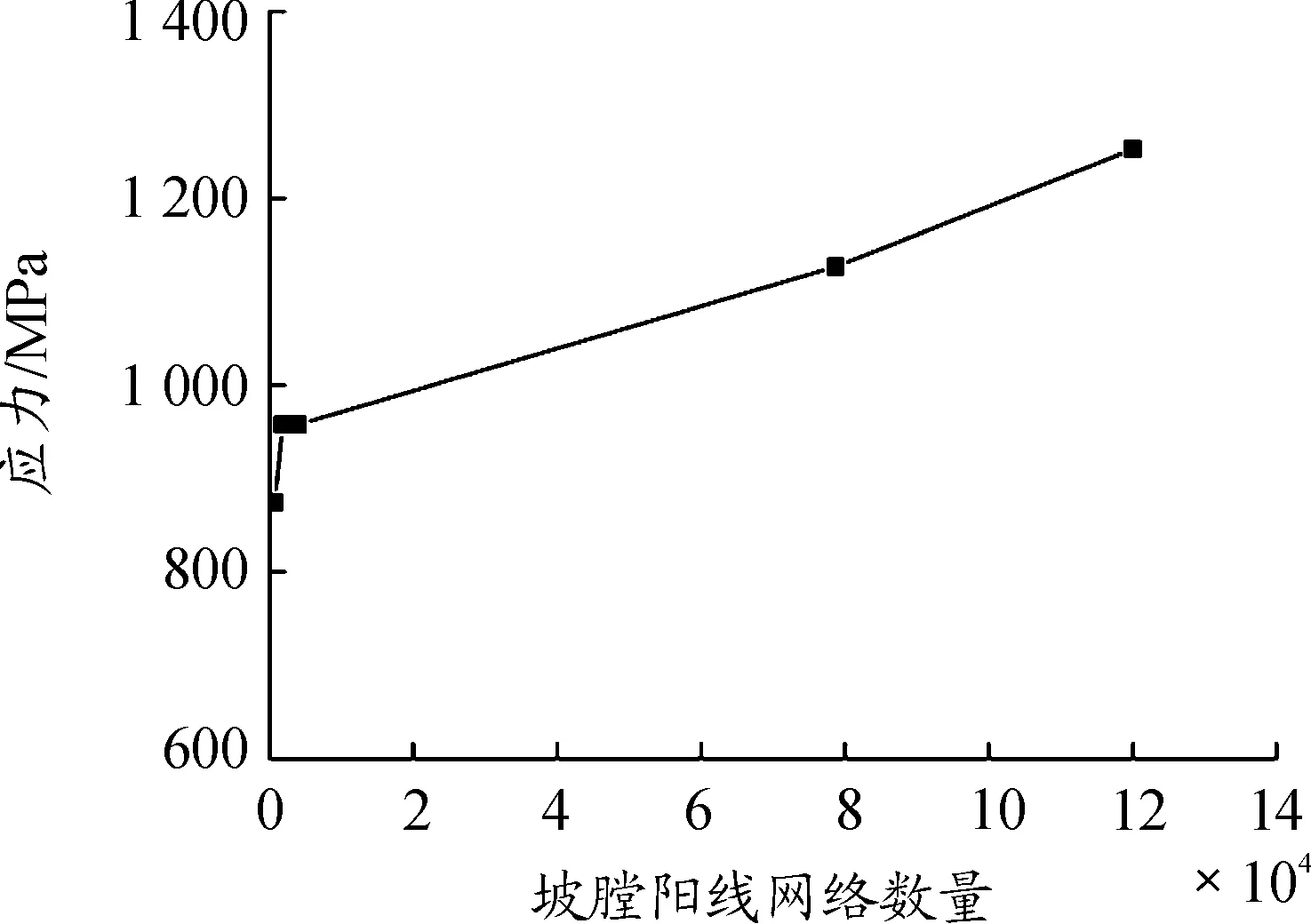
图4 不同坡膛阳线网格数量的应力峰值曲线
由图4可以看出,随着网格密度的增大,计算得到的应力峰值越来越大,但是方案2的应力峰值与方案3的应力峰值相近,这是由于这两种方案的网格密度差异不大。
2.3 网格密度对挤进阻力的影响
弹头在挤进膛线的过程中,受到坡膛的挤压作用使弹头表面产生刻痕,坡膛表面、阴线以及导转侧的力共同形成了弹头挤进过程中的挤进阻力。在有限元仿真时,挤进阻力可以看作是身管和被甲之间的作用力,获取5种方案条件下的挤进阻力变化数据,如图5所示。
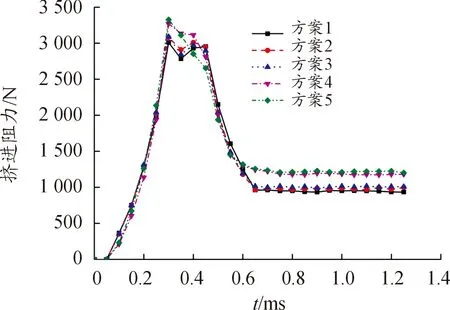
图5 不同网格密度下的挤进阻力曲线
从图5可以看出,在弹头挤进过程中,弹头受到的挤进阻力一开始迅速增大,达到最大值之后开始减小,最终到达一个较小的稳定值。方案1计算得到的挤进阻力峰值为3 010.41 N,方案2为3 081.99 N,方案3为3 088.83 N,方案4为3 270.06 N,方案5为3 327.12 N。不同坡膛阳线网格数量挤进阻力峰值曲线如图6所示。
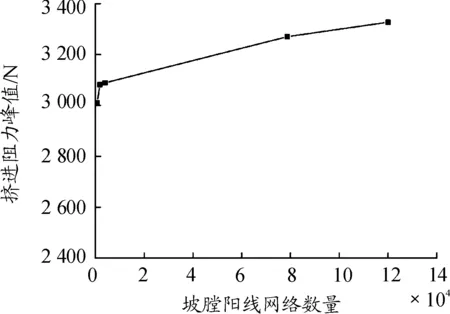
图6 不同坡膛阳线网格数量挤进阻力峰值曲线
由图6中5种方案的挤进阻力曲线对比可以看出,随着6条坡膛阳线网格密度的增加,获得的挤进阻力峰值更接近真实的挤进阻力峰值。
随着网格密度的增加,计算时间的也相应增长,5种方案的仿真时间、坡膛阳线应力峰值与挤进阻力峰值如表3所示。
从表3可以看出,随着网格密度的增加,计算得到的坡膛阳线应力峰值与挤进阻力峰值呈现增加的趋势,即计算精度逐渐提高,但是随着精度的提高仿真计算的时间也逐渐增加。从方案4到方案5,为增加计算精度付出的仿真时间代价较大,综合计算精度和时间成本,可以得出方案4是一种较优的网格划分方案,即坡膛阳线上最接近线膛处单元网格最大尺寸为0.033 28 mm。
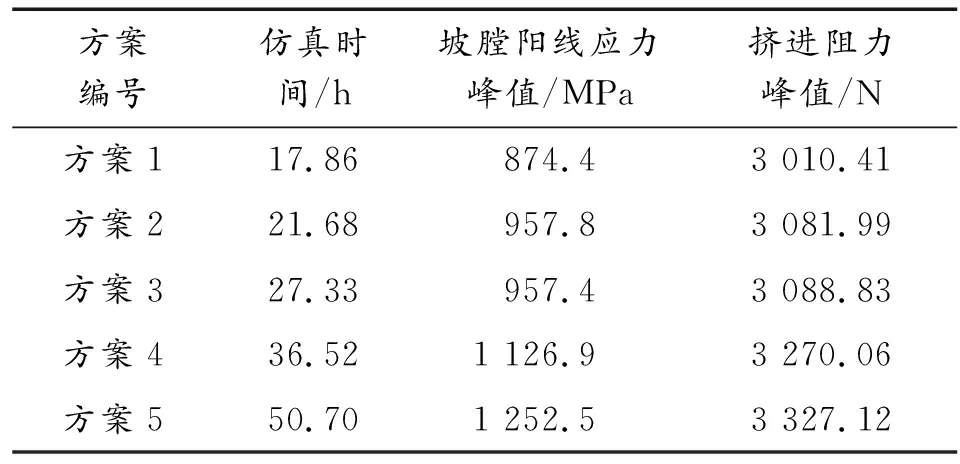
表3 不同网格密度下仿真时间和坡膛阳线应力峰值、挤进阻力峰值
3 阳线直径对弹头挤进过程的影响
身管在加工过程中存在制造误差,这些误差会影响阳线直径,而阳线直径的变化对弹头的挤进过程有着非常重要的影响。因此通过改变阳线直径来研究弹头挤进过程中挤进阻力、身管应力等受阳线直径的影响规律,在此基础上从降低挤进阻力及减小身管应力的角度出发对阳线直径进行优化设计。
3.1 阳线直径对挤进阻力的影响
根据前述网格密度研究结论选择最接近线膛元网格最大尺寸为0.033 28 mm时划分网格。身管阳线直径的变化是通过改变阳线直径大小来改变的。身管阳线的初始直径为5.80 mm,根据阳线的尺寸公差范围,选取阳线直径分别为5.82 mm、5.84 mm、5.86 mm、5.88 mm。分别对弹头挤进这5个不同阳线直径的身管的过程进行有限元建模分析,得到改变身管阳线直径后弹头受到挤进阻力随时间变化的曲线如图7所示。
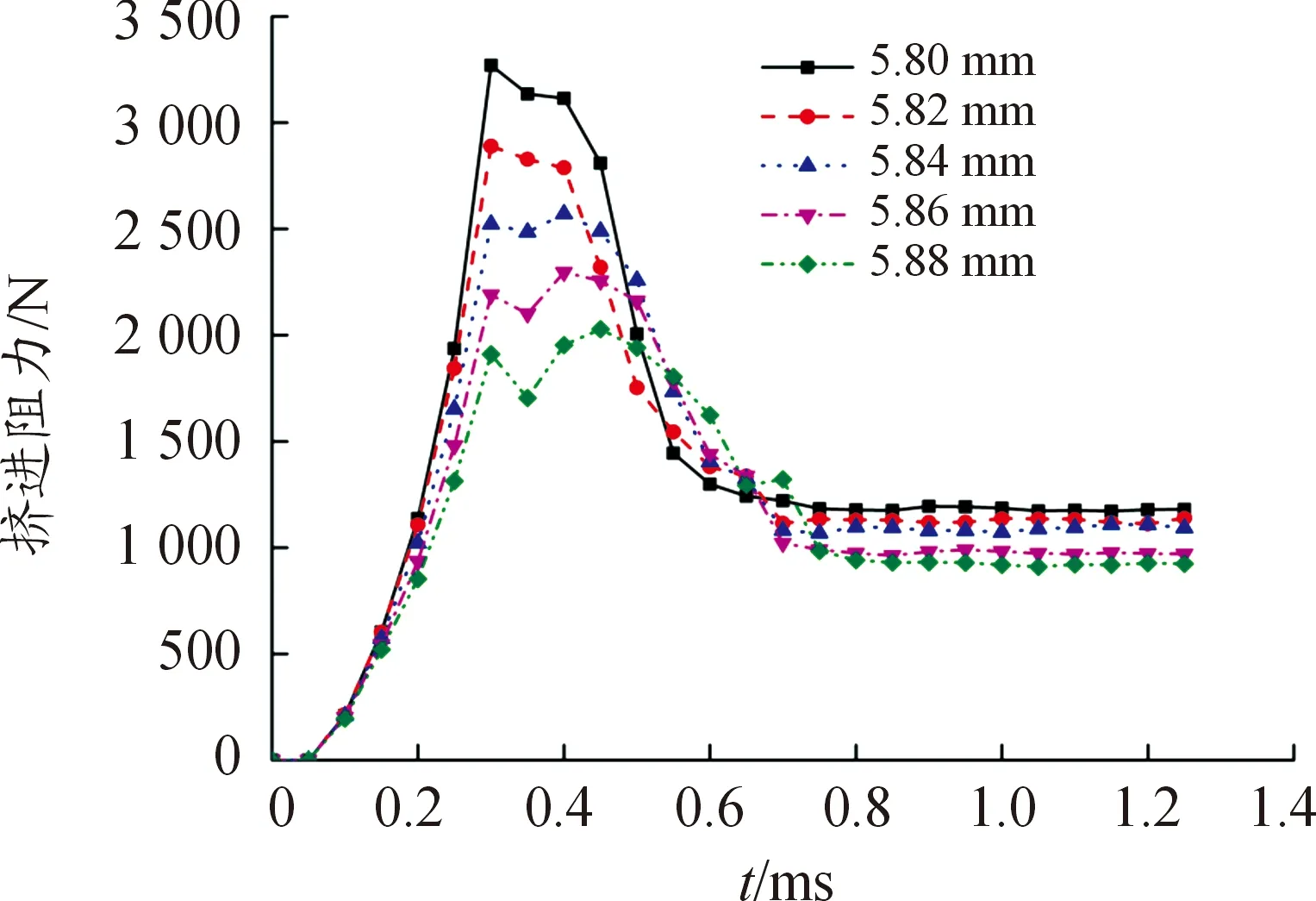
图7 不同阳线直径下的挤进阻力曲线
由图7可以看出,当阳线直径为5.80 mm时,挤进阻力峰值为3 270.06 N;当阳线直径为5.82 mm时,挤进阻力峰值为2 889.64 N;当阳线直径为5.84 mm时,挤进阻力峰值为2 570.58 N;当阳线直径为5.86 mm时,挤进阻力峰值为2 296.63 N;当阳线直径为5.88 mm时,挤进阻力峰值为 2 028.41 N。挤进阻力峰值随身管阳线直径的变化曲线如图8所示。
由图8可以看出,身管阳线直径逐渐增加时,挤进阻力峰值逐渐减小。并且也可以看出身管在挤进坡膛后,挤进阻力稳定值随着身管阳线直径增加也越来越小。为降低弹头挤进过程中的挤进阻力,在公差允许的范围内,应尽量增加身管的阳线直径。
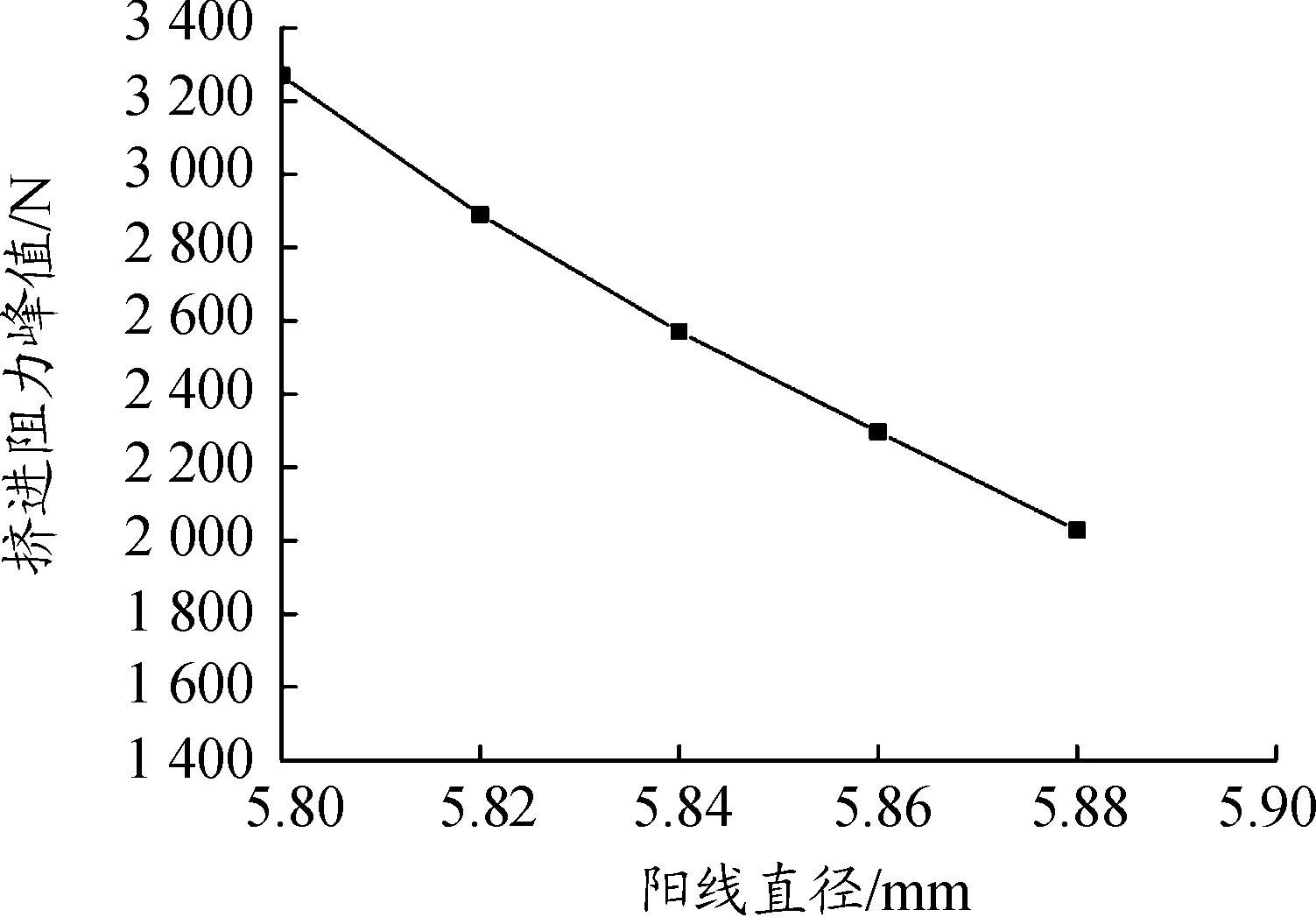
图8 不同阳线直径下挤进阻力峰值曲线
3.2 阳线直径对坡膛处应力的影响
选取前述坡膛导转侧的特征点1为研究对象,获取在不同阳线直径的身管变化下,该点在挤进过程中受到的应力随时间变化曲线如图9所示。
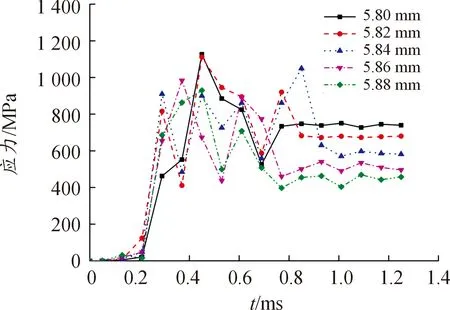
图9 不同阳线直径下特征点1的应力曲线
由图9可以看出,当阳线直径为5.80 mm时,特征点1处应力峰值为1 126.89 MPa;当阳线直径为5.82 mm时,特征点1处应力峰值为1 111.43 MPa;当阳线直径为5.84 mm时,特征点1处应力峰值为1 049.52 MPa;当阳线直径为5.86 mm时,特征点1处应力峰值为983.85 MPa;当阳线直径为5.88 mm时,特征点1处应力峰值为929.57 MPa。不同阳线直径下特征点1处应力峰值曲线如图10所示。
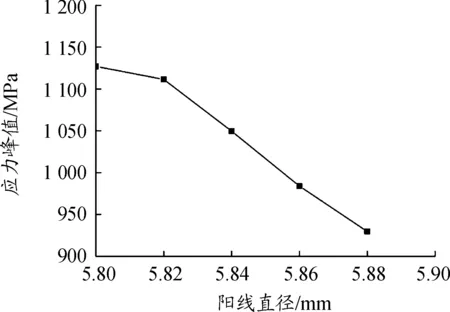
图10 不同阳线直径下特征点1处应力峰值曲线
由图10可以看出,随着身管阳线直径的增加,身管坡膛特征点1处的应力峰值越来越小。并且当阳线直径增加时,弹头挤进身管后达到的应力稳定值也越来越小,这是由于随着阳线直径的增加身管受弹头挤进身管时产生的变形也逐渐减小,从而导致挤进阻力和应力的减小。为减小挤进过程中身管的应力,在公差允许的范围内,也应尽量增加身管的阳线直径。
3.3 阳线直径对弹头变形的影响
选取5种不同阳线直径的身管进行数模模拟分析,得到弹头挤进五种不同阳线直径身管后,弹头被甲的应力云图和刻痕分布图如图11和图12所示。
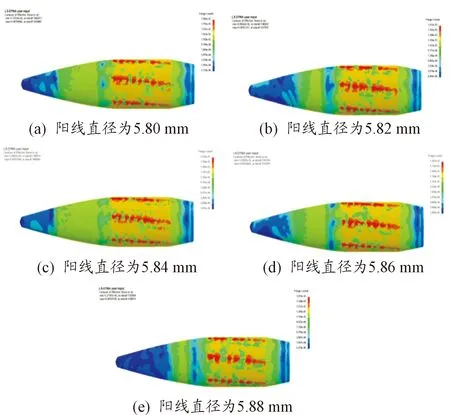
图11 不同阳线直径下弹头挤进完成后被甲应力云图
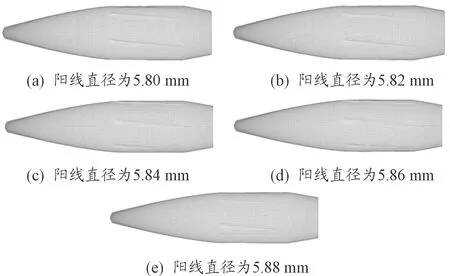
图12 不同阳线直径下弹头挤进完成后被甲刻痕分布图
从图11和图12可以看出,随着身管阳线直径的增加,弹头被甲的应力峰值逐渐减小,刻痕程度逐渐减小,这是由于随着阳线直径增大,弹头挤进身管后被甲产生的变形减小,从而导致被甲的应力和产生的刻痕程度均降低。
4 结论
1) 对某小口径枪弹挤进不同网格密度身管的过程进行仿真,综合考虑计算精度和计算时间成本,坡膛阳线上最接近线膛处单元网格最大尺寸0.033 28 mm时最佳。
2) 随着阳线直径的增加,弹头挤进过程中的挤进阻力峰值和身管坡膛导转侧应力峰值逐渐减小,即弹头越容易挤进身管,挤进后的被甲变形程度减小,身管所受应力也越小,有利于提高身管寿命。为降低挤进过程中的挤进阻力以及身管应力,应在工程许可的范围内尽量增加阳线直径。
