计及大地影响的轨道电路钢轨自阻抗计算研究

张友鹏，王东，赵斌，贾智

计及大地影响的轨道电路钢轨自阻抗计算研究

张友鹏，王东，赵斌，贾智

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

钢轨自阻抗是轨道电路计算分析的重要参数之一，其值大小直接影响轨道电路的传输性能。针对考虑大地影响，利用Carson公式计算钢轨自阻抗时存在积分上限难以确定及被积函数高频震荡问题。提出采用核函数分段线性逼近法求解被积函数，并利用截断法将无穷上限积分转换为有限积分，得到精度更高的钢轨自阻抗计算方法。建立轨道电路模型，采用有限元法仿真计算，验证该计算方法的正确性。将该方法计算结果、Carson单项近似法计算结果同仿真结果对比，验证该方法的计算精度。利用该方法分析电流频率、轨道高度及大地电导率对钢轨自阻抗的影响规律。研究结果表明：该方法计算结果与仿真结果误差小于6%，计算精度更高，且正确反映了各参数对钢轨自阻抗的影响规律，从而为精确计算轨道电路钢轨自阻抗及分析轨道电路传输特性提供可靠的理论支撑。

钢轨自阻抗；Carson公式；核函数；分段线性逼近；截断法；有限元

电气化铁路中，轨道电路作为列车运行控制系统的关键设备，主要用于传递列车控制信息、检查轨道线路是否空闲，以保证列车安全高效的运行[1]。钢轨阻抗作为轨道电路设计中重要的电气参数，其值是影响轨道电路传输性能的关键因素。而钢轨自阻抗作为钢轨阻抗的一部分，准确计算钢轨自阻抗是分析轨道电路传输特性及设计轨道电路的基础，同时，也为牵引供电系统建模时钢轨自阻抗的计算提供新的计算方法[2]。钢轨铺设在地面之上，类似于架空导体，而针对架空导体自阻抗的计算，国内外学者做了大量研究。Carson等[3-4]研究了以大地为回路的架空导线阻抗计算问题，为钢轨自阻抗计算提供了理论基础。Butler-Purry等[5]采用Carson公式的无穷级数展开，仅取第1项近似计算了架空导线的自阻抗，计算结果误差较大。Deri等[6]使用复穿透公式，考虑大地的集肤深度，近似计算了架空导体的自阻抗、互阻抗。朱军等[7]运用复数镜像法，计算了架空导线-地回路阻抗。杜学龙等[8]考虑大地影响，基于Carson简化公式(Deri地阻抗公式)，采用泰勒级数展开计算了相邻轨道电路的互阻抗，并分析了大地电导率、轨道高度等参数对互阻抗的影响，未提及钢轨自阻抗的计算，且计算公式过于简化，忽略了阻抗计算中的电阻部分。Hill等[9]基于电磁场有限元法仿真计算了单线轨道电路的钢轨阻抗，分析了电流频率、幅值、大地电导率等参数对钢轨自、互阻抗的影响，并使用Carson阻抗公式和实验测量数据进行验证，表明有限元法可以准确计算钢轨阻抗，但计算所需资源较大且对操作人员有技术要求。DU等[10]将钢轨自阻抗分解为内阻抗和外阻抗，分别使用有限元法和Carson公式求解内、外阻抗，其中，求解外阻抗时，采用渐近近似法求解了Carson公式，导致计算结果精度较低。焦彦军等[11]基于Carson阻抗公式，提出函数替代法，替代Carson公式中震荡的被积函数，推导出计算架空传输线路分布参数的新方法，但计算过程比较复杂。ZOU等[12-13]研究架空导体互阻抗时，采用矩函数方法和截断法计算了Carson互阻抗公式，但未提及导体自阻抗的计算。目前，针对架空导线自阻抗的计算一般采用有限元法和Carson公式，有限元法计算精度高，但所需计算资源较大，而Carson公式难以直接计算，多数采用近似计算，计算精度低。基于以上分析，本文基于Carson公式计算轨道电路钢轨自阻抗，针对该阻抗公式中存在被积函数高频震荡、积分区间无限问题，采用核函数分段线性逼近法对阻抗公式中的被积函数进行计算，并利用截断法对积分区间进行截断，得到钢轨自阻抗计算方法。为验证该计算方法的合理性和准确性，建立轨道电路钢轨自阻抗电磁场模型，基于有限元法仿真计算钢轨自阻抗，并采用Carson单项近似法直接解析求解，将本文计算结果、Carson单项近似法计算结果同有限元仿真结果对比，本文方法误差小于6%，得到计算精度更高的自阻抗计算方法。利用该方法分析电流频率、大地电导率、轨道高度对钢轨自阻抗的影响，从而为钢轨自阻的精确计算及抗轨道电路传输特性分析提供理论依据。

1 钢轨自阻抗公式

1.1 钢轨自阻抗

钢轨自阻抗是指考虑大地影响的钢轨自身阻抗，主要包括钢轨的内阻抗与外阻抗，其中外阻抗是指钢轨的纵向阻抗(当钢轨与大地均为理想导体)及钢轨-地回路阻抗(当大地为有损导体)。对于钢轨内阻抗，其仅与钢轨的材料参数、电流大小、频率相关，与大地无关。而对于外阻抗，其大小与电路结构、大地电导率有关。考虑大地影响，单线轨道简化模型如图1所示。本文仅计算钢轨自阻抗，未涉及钢轨互阻抗的计算，在理想状态下，2根钢轨的自阻抗相等，因此，计算时仅计算单根钢轨的自阻抗。

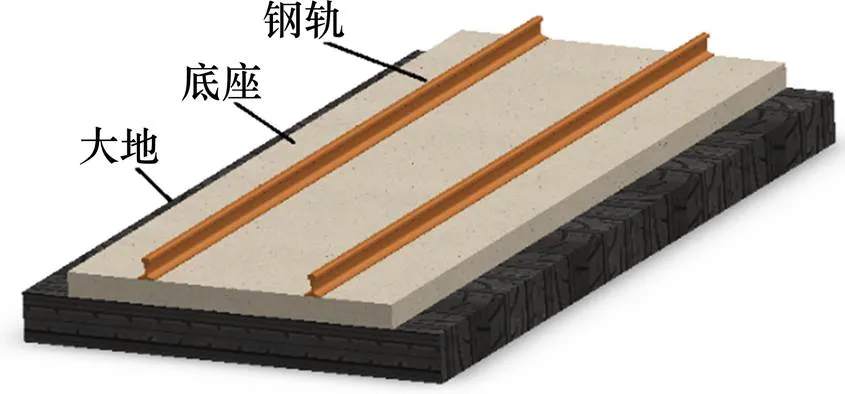
图1 单线轨道简化模型

1.2 Carson阻抗计算公式

1926年，Carson提出以大地为回路的架空线阻抗计算公式，为电流流经大地情况下架空线阻抗计算提供理论基础。图2为地面上单条架空线，架空线a位于地面上一定高度。

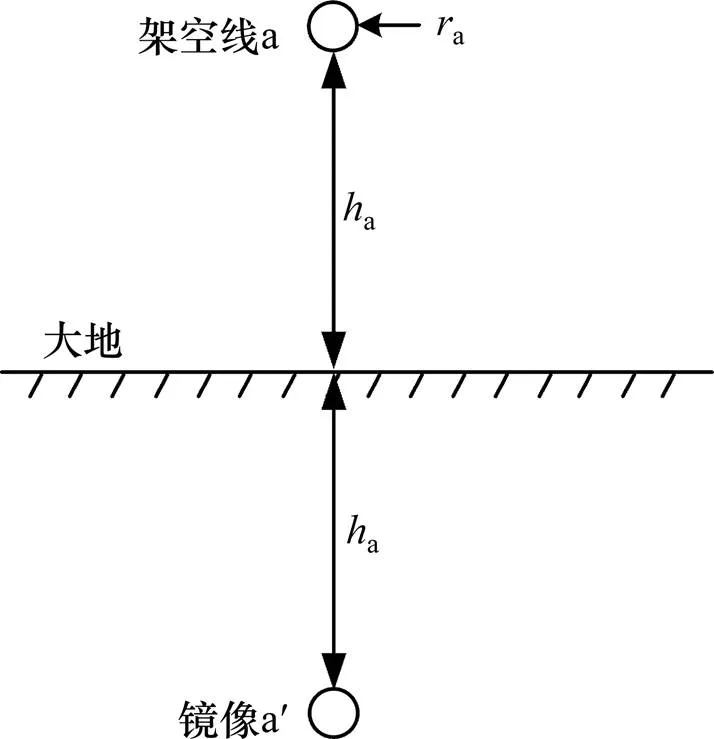
图2 地面上单条架空线

考虑大地影响，基于Carson公式，架空线a的自阻抗可表示为

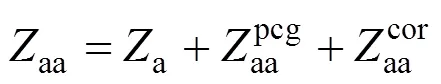
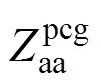
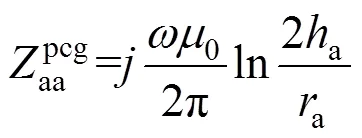
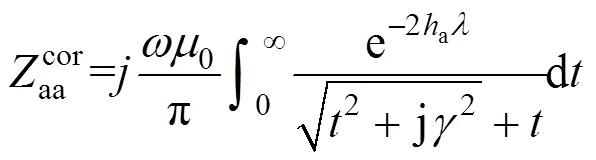
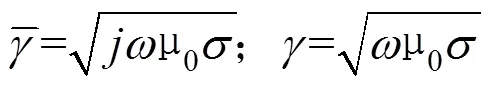
式中：为大地电导率。

从式(3)可知，架空线-地回路阻抗表达式中含无穷上限的震荡积分，直接计算该积分存在一定困难，因此，本文提出核函数分段线性逼近法和截断法计算该阻抗表达式中的架空线-地回路阻抗。

1.3 架空线-地回路阻抗计算

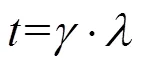
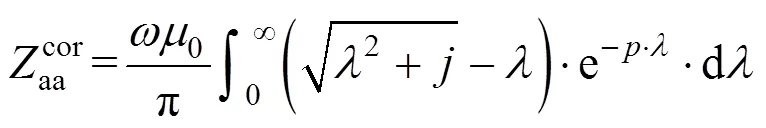
为计算式(5)，首先定义核函数为

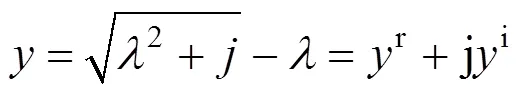
由式(6)可知，核函数与频率、大地电导率等无关，仅与积分变量有关。核函数实部、虚部表示为

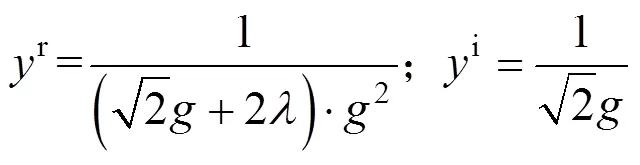
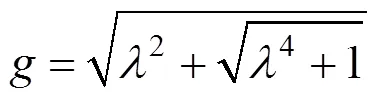
从图3和图4中可以看出，核函数的实部与虚部随积分变量的增大而减小，甚至逐渐趋于0，其实部较虚部而言，衰减更快，即核函数的实部与虚部均收敛。

其次，采用截断法对无穷上限积分区间进行截断，并将式(5)中积分拆分为实部积分和虚部积分两部分，其可表示为

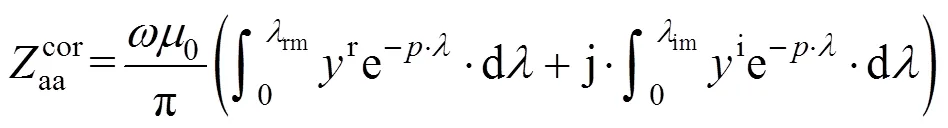
式中：和分别为实部和虚部积分区间的上限截断值。

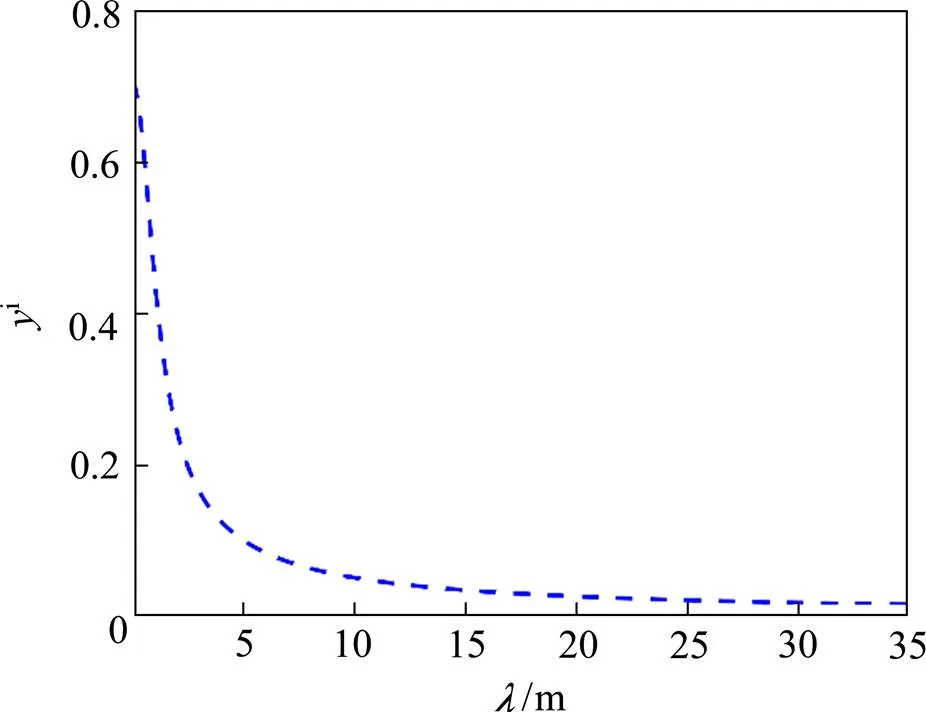
图4 核函数虚部

根据核函数的渐近近似，由式(6)和式(7)可知，核函数可近似为

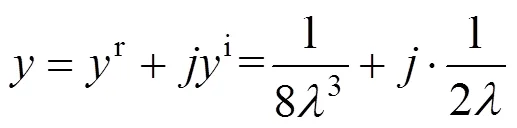
根据式(8)和式(9)，得到实部与虚部积分区间的积分上限值计算公式为

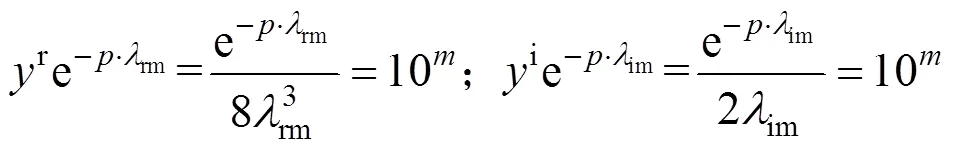
式中：是表征核函数近似精度的数量级大小，取=-10。

式(10)为非线性方程，无法直接求解计算方程的根，而牛顿迭代法适用于非线性方程求解。首先，将非线性方程表示为函数，通过对函数作泰勒展开，省略掉二次项，得到函数的线性近似式，并不断用变量的旧值递推新值来进行迭代，得到方程的近似解。在Matlab软件中可以直接编程计算[15]。

基于以上计算，将无穷积分区间截断为有限积分区间。在此基础上，利用核函数分段线性逼近法求解式(8)中的实部积分和虚部积分。对于实部和虚部积分区间，进行间隔采样，利用线性近似逼近两采样点之间的曲线，实部积分核函数分段线性逼近原理如图5所示，虚部积分核函数分段线性逼近与其相同。

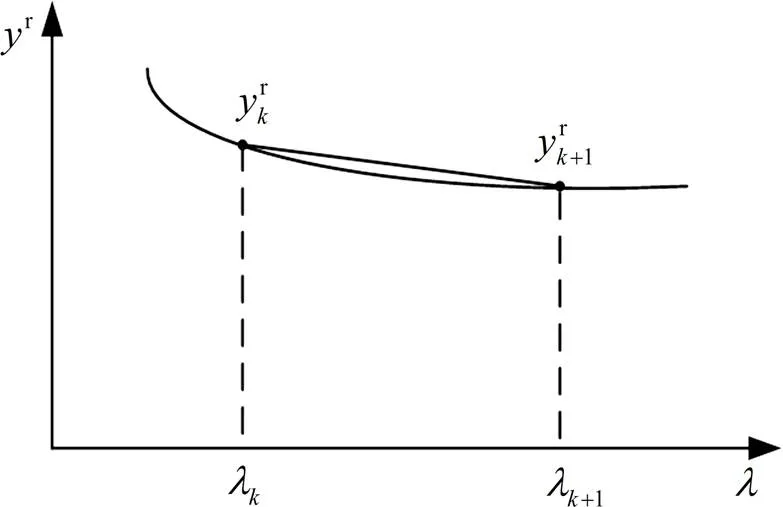
图5 核函数实部分段线性逼近

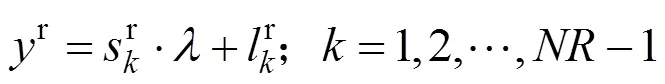
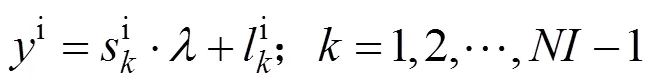
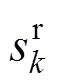
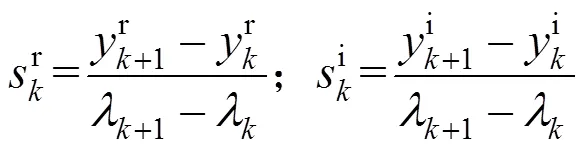
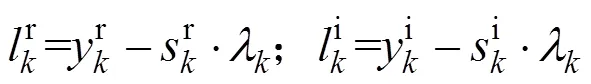
根据式(11)，利用核函数分段线性逼近和截断法计算架空线-地回路阻抗，可得式(15)，采用分部积分法直接计算式(15)中的积分，可得到式(16)。

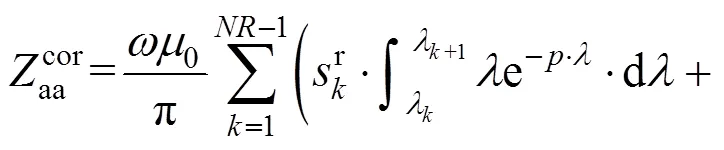
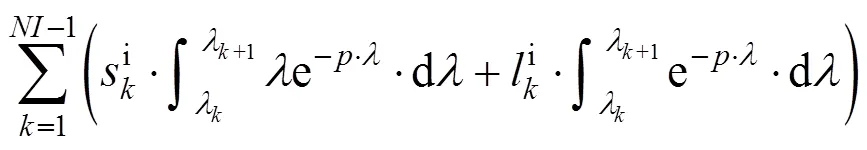
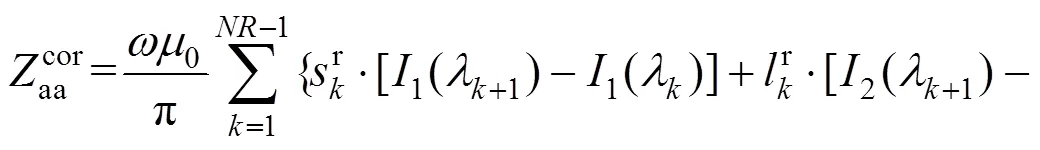
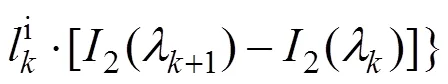
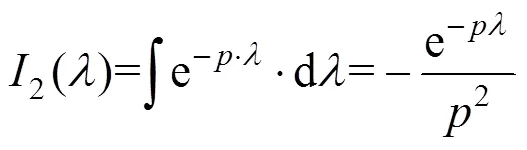
2 有限元仿真

本文选取有砟轨道结构，根据有砟轨道结构组成建立轨道电路电磁场仿真模型。由于实际情况下钢轨处于无限大开放区域，仿真计算时，为处理无限大开区域问题，可使开区域半径为钢轨等效半径(采用周长相等原则计算钢轨的等效半径)的若干倍，且通过柱坐标变化，采用无限元域将无限大区域变换为有限区域。仿真中使用60 kg/m的P60型钢轨，电导率为6×106s/m，且钢轨是铁磁材料，其磁导率参考文献[16]中钢轨的B-H曲线。钢轨作为轨道电路信号电流和牵引回流的通道，信号电流大小为毫安级，频率范围为1 700～2 600 Hz，而牵引回流一般为几百安培，频率为工频50 Hz。因此，激励设为正弦工频电流，同时为研究轨道电路钢轨自阻抗在宽频范围内的变化，进行0～10 kHz的参数扫频。对于电磁场模型网格剖分时，由于钢轨在交流电流作用下出现集肤效应，需根据集肤因子大小对钢轨部分进行网格剖分。钢轨剖分如图6(a)所示。由于集肤效应，电流主要集中分布在钢轨表面，钢轨在频率为2 600 Hz时集肤效应如图6(b)所示。单根钢轨整体模型剖分如图7所示。钢轨自阻抗中的自电阻、自电感可通过欧姆损耗和磁场储能进行计算。

钢轨自阻抗由钢轨内阻抗与外阻抗组成，由于钢轨截面不规则，呈“工”字形，且钢轨为铁磁性材料，目前无法解析求解钢轨内阻抗，因此，本文亦采用有限元法计算内阻抗；而钢轨外阻抗仅与钢轨外部磁场、电路结构及大地有关，与钢轨内部磁场无关，因此，利用Carson公式计算外阻抗，并采用本文计算方法计算外阻抗表达式中的架空线-地回路阻抗。其中，针对钢轨的不规则形状，利用周长相等原则计算钢轨等效半径，将钢轨等效为圆柱形导体。

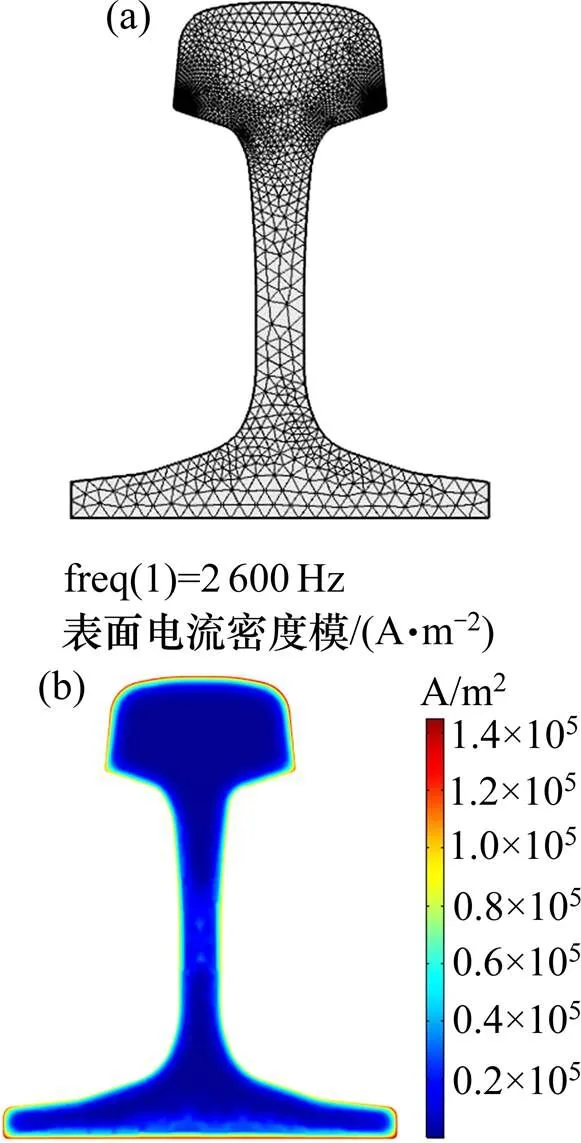
(a) 钢轨网格剖分；(b) 钢轨集肤效应

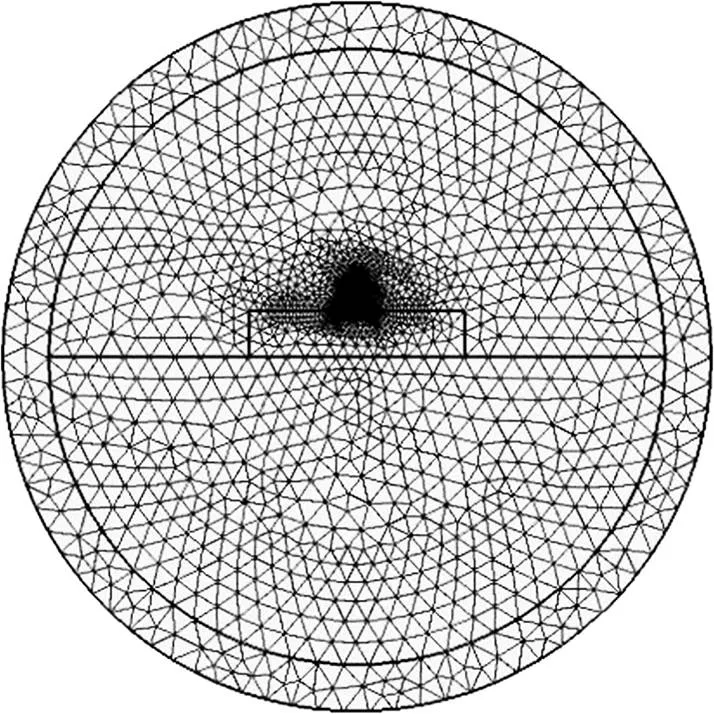
图7 单根钢轨有限元计算模型网格剖分

P60型钢轨等效半径为0.106 6 m，钢轨离地高度为0.03 m，大地电导率为0.01 s/m，频率在0～10 kHz范围内。根据以上参数，利用本文所提方法计算钢轨外阻抗。对于钢轨内阻抗，由于其材料的铁磁特性，采用有限元法可直接计算[17]。同时，文献[9]利用有限元法计算了钢轨的自、互阻抗，并以BS113A型钢轨为例计算了钢轨的自、互阻抗，验证了有限元法的正确性，表明有限元法可以准确计算钢轨阻抗。因此，为验证本文所提方法的正确性及计算精度，利用有限元法对单根钢轨整体模型仿真计算，并采用文献[18]中的Carson单项近似法解析计算。其中，内阻抗均采用有限元法计算，因此，仅需比较钢轨外阻抗的值，将本文计算方法的计算结果、Carson单项近似法的计算结果同有限元仿真结果对比，并定义相对误差描述计算方法的精度，相对误差计算式为

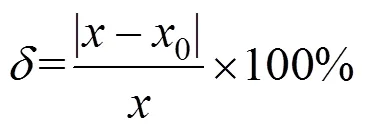
式中：表示本文方法和Carson单项近似法计算的外阻抗值，0表示有限元法计算的外阻抗值，且外阻抗值中包括自电阻和自电感。

根据计算结果及仿真结果，利用式(17)，计算出外阻抗中自电阻和自电感相对误差如图8和图9所示，图中1和2分别表示本文方法与有限元法及Carson单项近似法与有限元法的自电阻相对误差，3和4分别表示本文方法与有限元法及Carson单项近似法与有限元法的自电感相对误差。

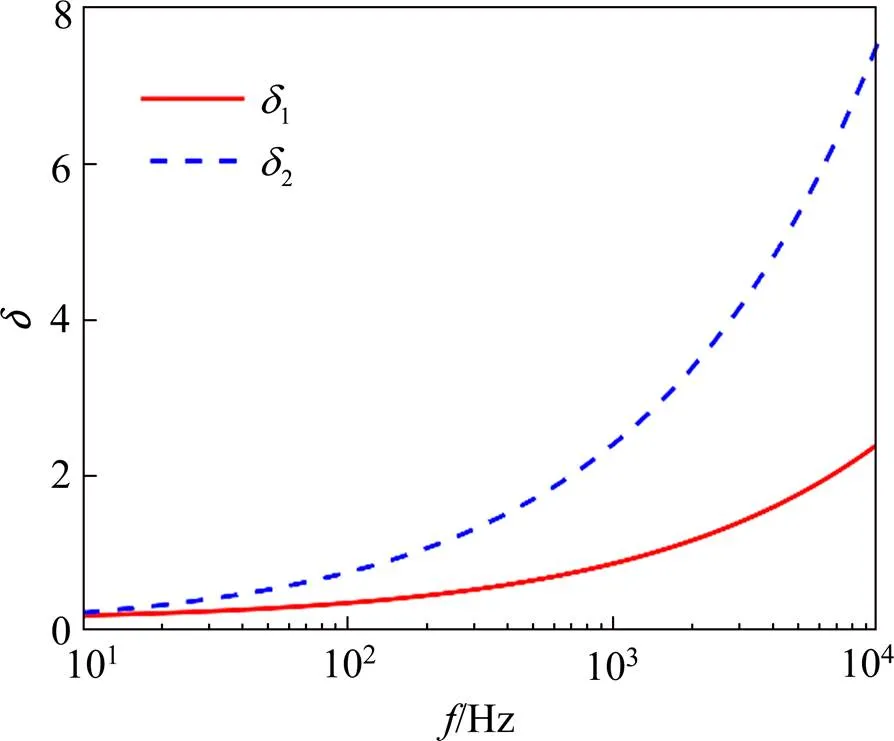
图8 自电阻计算误差

对于自电阻的误差，由图8中可知，1小于2，即本文方法误差小，且随着频率的增大，1与2均有增大趋势，但1的增大趋势远小于2在10 kHz时，相对误差1在4%以内。

对于自电感的误差，由图9中可知，随着频率的增大，3逐渐增大，当频率超过大约6 200 Hz时，3开始减小，且整个频率范围内，3的最大值在6%以内，而4随频率的增大一直呈现增大趋势，误差较大。

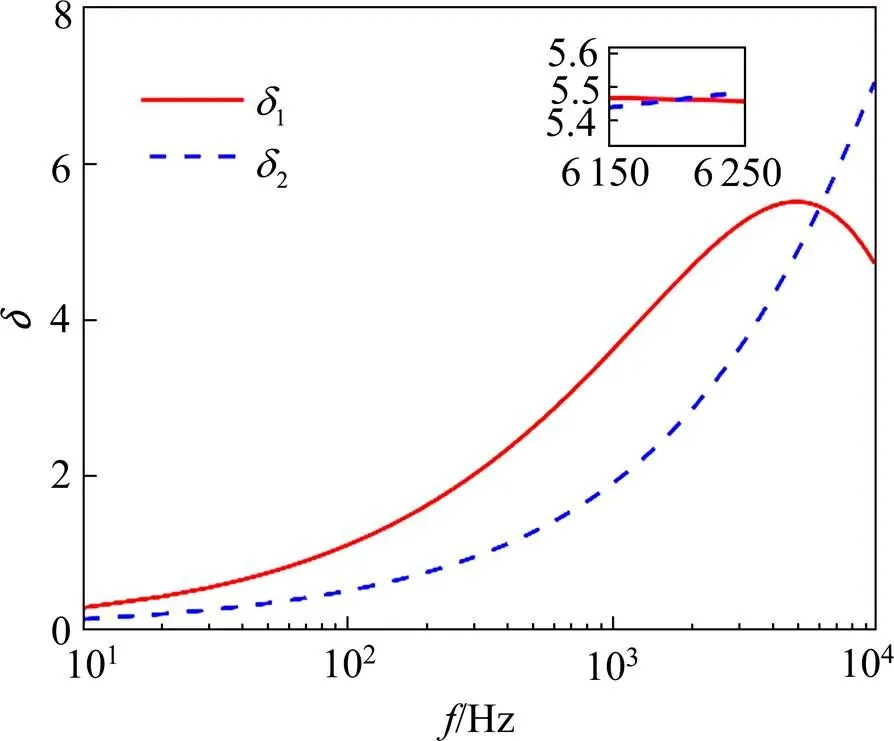
图9 自电感计算误差

3 钢轨自阻抗影响因素分析

3.1 电流频率影响

轨道电路既是轨道电路信号电流的通道，也是牵引回流的通道，由于信号电流与牵引回流频率分布较宽，为此，在0～10 kHz范围内研究频率变化对钢轨自阻抗的影响。根据本文计算方法，计算钢轨外阻抗，并利用有限元计算钢轨内阻抗。并将其表示为钢轨自电阻与自电感，计算结果如图10和图11所示，将图10中的线性横坐标转换为对数坐标，可以更明显的看出自电阻随电流频率的变化规律。

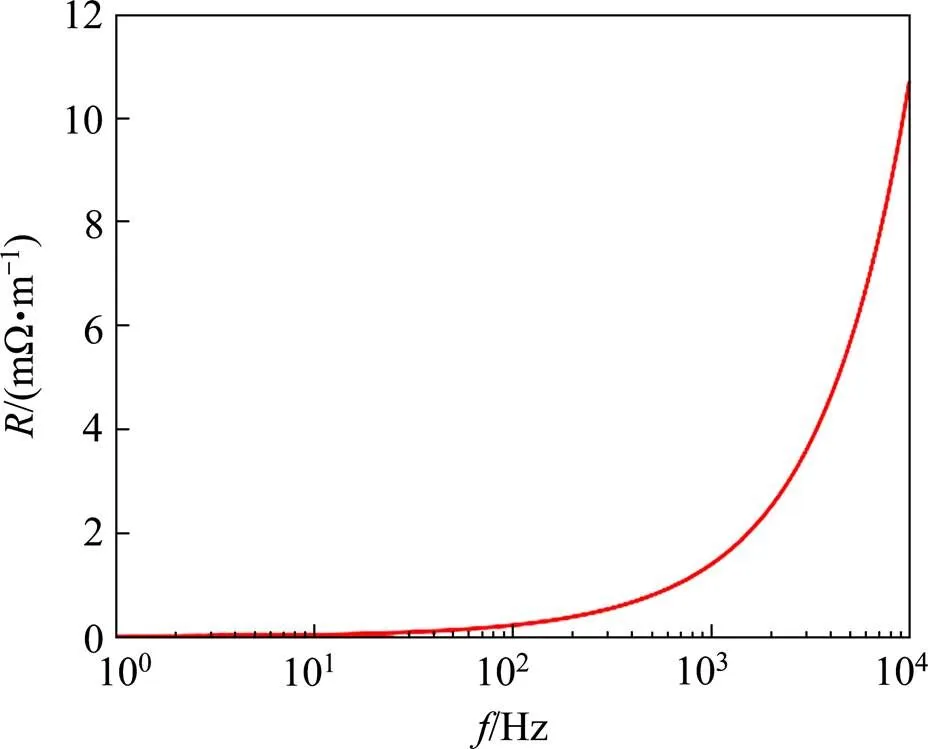
图10 自电阻与频率的关系

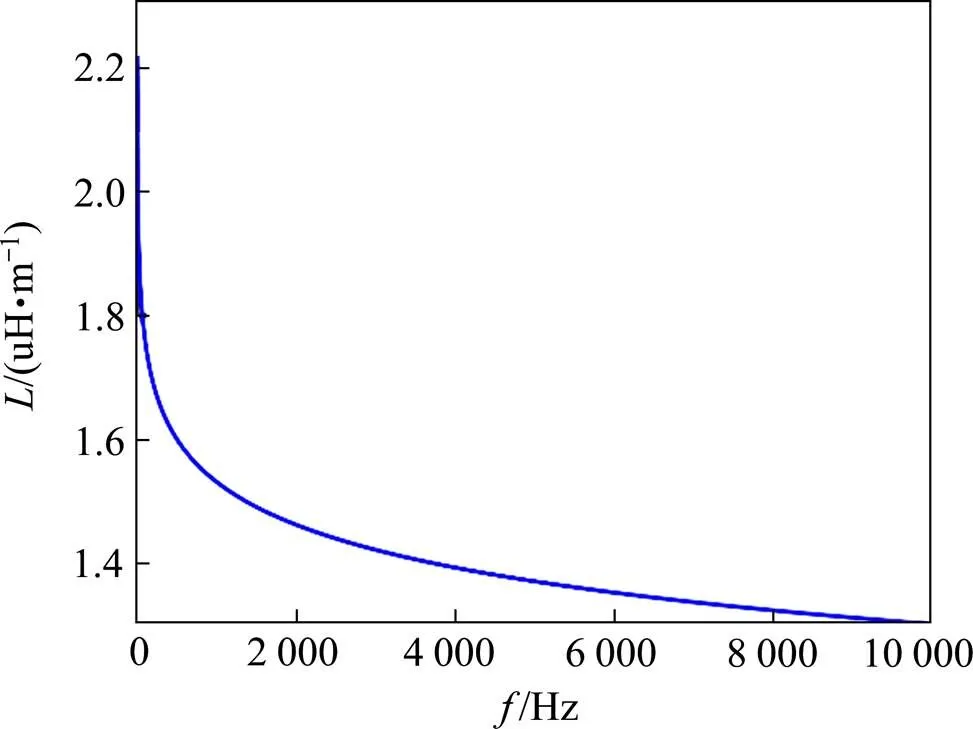
图11 自电感与频率的关系

由图10可知，钢轨自电阻随电流频率的增大而增大，当电流频率较低时，自电阻变化趋势缓慢，而当频率较高时，自电阻随频率变化的趋势比较明显，其主要是由于随着电流频率的增加，钢轨和大地的集肤效应更加明显，且大地为有损媒质，因此，钢轨自电阻随着电流频率的增加而增大。

由图11可知，钢轨自电感随着电流频率的增大而减小，当频率较低时，自电感变化趋势显著，而随着频率的增加，自电感变化趋势变缓，其主要是由于钢轨和大地存在集肤效应，随着电流频率的增加，电流集中分布在钢轨和大地表面一定深度内，从而导致钢轨和大地内部电感减小，致使自电感减小。

3.2 钢轨高度及大地影响

轨道线路铺设环境复杂，不同的轨道结构(路基段、桥梁区段、隧道)及地理环境都将影响轨道电路的传输特性。对于钢轨自阻抗的计算，由于钢轨铺设在不平整的大地上，并且途径区域的土壤环境复杂，为此，需考虑钢轨高度及大地电导率对钢轨自阻抗的影响。钢轨中的电流主要为幅值几百安培的牵引回流，因此，设定电流频率为工频50 Hz，而对于大地电导率，由于其与大地湿度、温度、大地结构等因素有关，由于实验条件限制，未实际测量其变化。为此，根据文献[9]中大地电导率的数值范围，将其设置为0.001～1 S/m，利用本文计算方法计算钢轨高度及大地电导率对钢轨自阻抗的影响。

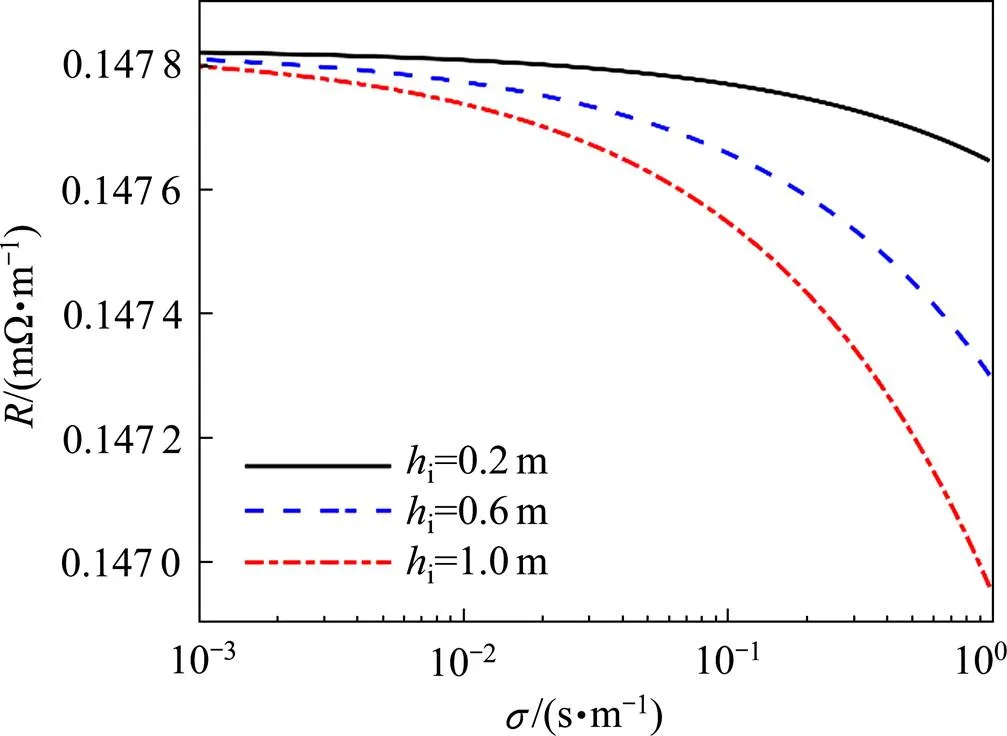
图12 电阻与大地电导率的关系

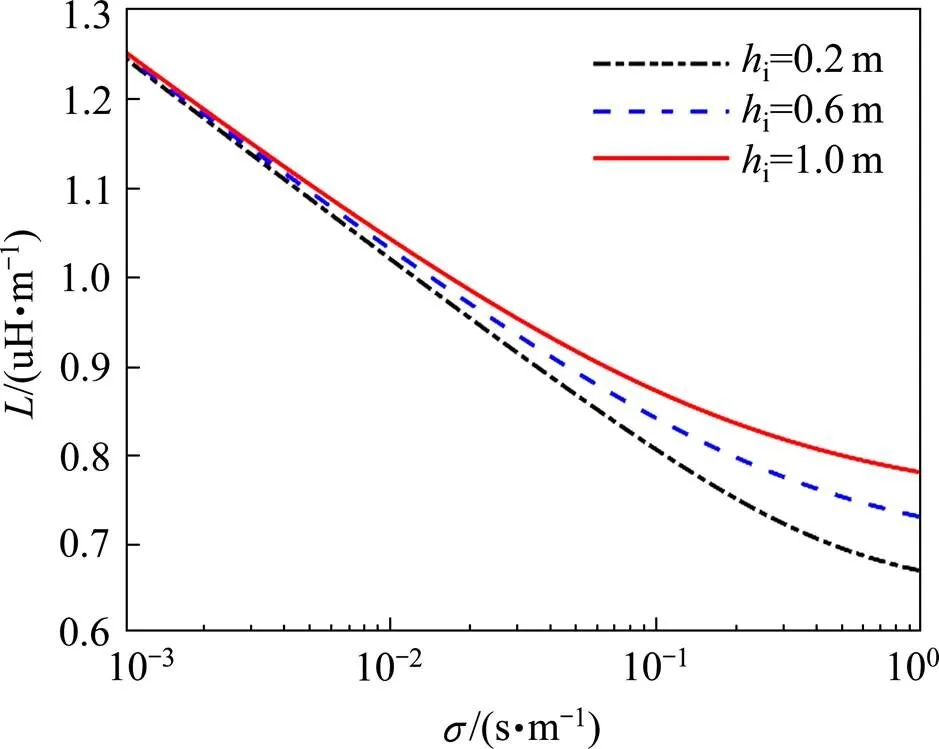
图13 电感与大地电导率的关系

从图12中可以看出，随着大地电导率的增加，钢轨自电阻呈现逐渐减小的趋势，尤其在电导率接近于1时，变化显著；在同一大地电导率下，轨道高度越高，自电阻越小，且大地电导率较小时，钢轨高度对自电阻影响较小，大地电导率较大时，钢轨高度对自电阻影响较大。

从图13中可以看出，钢轨自电感值随大地电导率的增加而减小，且变化趋势在大地电导率整个变化范围内均比较显著；在同一大地电导率下，轨道高度越高，自电感越大，且在大地电导率较小时，钢轨高度对自电感影响较小，大地电导率较大时，钢轨高度对自电感影响较大。

4 结论

1) 考虑大地影响，基于核函数分段线性逼近法和截断法计算钢轨自阻抗时，避免了直接采用Carson公式求解困难问题，将本文方法计算结果和Carson单项近似法计算结果同有限元仿真结果比较，本文计算结果误差小于6%，计算精度更高。

2) 利用本文方法计算分析钢轨自电阻与自电感随电流频率变化规律，表明自电阻随电流频率的增大而增大，而自电感随电流频率的增大而减小。

3) 给出了自电阻与自电感随大地电导率、轨道高度的变化曲线。表明自电阻随大地电导率的增大而减小，且轨道高度越高，自电阻越小；自电感随大地电导率的增大而减小，且轨道高度越高，自电感越大。

4) 本文方法可以更准确地计算钢轨自阻抗，从而为轨道电路传输性能分析及轨道电路设计中钢轨自阻抗的计算提供了一种新的思路。

[1] 张汉花, 邹军, 王智新, 等. 阻抗分解法及其在无砟轨道阻抗求解中的应用[J]. 电工技术学报, 2017, 32(12): 164-170. ZHANG Hanhua, ZOU Jun, WANG Zhixin, et al. Impedance decomposition method and its application in calculating the impedance of ballastless track[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 164-170.

[2] 朱冰, 刘中田, 周果. 基于电磁场模型的轨道电路钢轨阻抗研究[J]. 铁路计算机应用, 2014, 23(5): 52-56, 59. ZHU Bing, LIU Zhongtian, ZHOU Guo. Study on track circuit impedance based on electromagnetic field model[J]. Railway Computer Application, 2014, 23(5): 52-56, 59.

[3] Carson John R. Wave propagation in overhead wires with ground return[J]. Bell Labs Technical Journal, 1926, 5(4): 539-554.

[4] Papagiannis G K, Tsiamitros D A, Labridis D P, et al. A systematic approach to the evaluation of the influence of multilayered earth on overhead power transmission lines[J]. IEEE Transactions on Power Delivery, 2005, 20(4): 2594-2601.

[5] Butler-Purry, Karen. Distribution system modeling and analysis[J]. IEEE Power & Energy Magazine, 2012, 11(3): 106-108.

[6] Deri A, Tevan G, Semlyen A, et al. The complex ground return plane a simplified model for homogeneous and multi-Layer earth return[J]. IEEE Power Engineering Review, 1981, PER-1(8): 31-32.

[7] 朱军, 吴广宁, 龚宏奎, 等. 大地分层结构条件下架空线路系统导线—地回路阻抗的计算分析[J]. 高压电器, 2014, 50(2): 29-34. ZHU Jun, WU Guangning, GONG Hongkui, et al. Calculation and study of impedance of conductor-earth circuits for overhead line systems with layered soil structure[J]. High Voltage Apparatus, 2014, 50(2): 29-34.

[8] 杜学龙, 王智新, 邹军. 考虑大地影响高速铁路轨道电路互阻抗快速计算简化公式[J]. 电工技术学报, 2016, 31(4): 1-6. DU Xulong, WANG Zhixin, ZOU Jun. A fast and simplified formula for calculating the mutual impedance with the earth return of the high-speed railway track circuit[J]. Transactions of China Electrotechnical Society, 2016, 31(4): 1-6.

[9] Hill R J, Brillante S, Leonard P J. Railway track transmission line parameters from finite element field modelling: Series impedance[J]. IEE Proceedings on Electric Power Applications, 1999, 146(6): 647-660.

[10] DU X, ZOU J, WANG Z. Calculation of the impedance of a rail track with earth return for the high-speed railway signal circuit using finite-element method[J]. IEEE Transactions on Magnetics, 2015, 51(3): 1-4.

[11] 焦彦军, 于江涛, 王增平. 计算架空线路分布参数的新方法[J]. 电力系统及其自动化学报, 2015, 27(4): 55-60. JIAO Yanjun, YU Jiangtao, WANG Zengping. New calculation method of overhead transmission line distributed parameters[J]. Proceedings of the CSU-EPSA, 2015, 27(4): 55-60.

[12] ZOU J, Lee J B, CHANG S H. An efficient algorithm for calculating the earth return mutual impedance of conductors with asymptotic extraction technology[J]. IEEE Transactions on Electromagnetic Compatibility, 2009, 51(2): 416-419.

[13] 邹军, 张汉花, 乔骥. 快速计算架空与水平双层大地埋地导体间互阻抗的矩函数方法[J]. 南方电网技术, 2016, 10(1): 6-10, 31. ZOU Jun, ZHANG Hanhua, QIAO Ji. Moment function method of fast mutual impedance calculation between overhead and underground conductor in horizontal two-layered soil[J]. Southern Power System Techonlogy, 2016, 10(1): 6-10, 31.

[14] 邹军, 赵科, 蒋陶宁. 涡流无损检测中的广义索末菲尔德积分快速计算[J]. 中国电机工程学报, 2009, 29(21): 119-123. ZOU Jun, ZHAO Ke, JIANG Taoning. Fast approach for calculating generalized Sommerfeld integrals in eddy current nondestructive tests[J]. Proceedings of the Chinese Society for Electrical Engineering, 2009, 29(21): 119-123.

[15] 张小鸣, 李永新. 基于牛顿迭代法的高精度快速开方算法[J]. 电力自动化设备, 2008, 28(3): 75-77. ZHANG Xiaoming, LI Yongxin. High-precision and fast square root algorithm based on Newton iteration method[J]. Electric Power Automation Equipment, 2008, 28(3): 75-77.

[16] 李群湛, 贺建闽. 牵引供电系统分析[M]. 成都: 西南交通大学出版社, 2007: 70-101.LI Qunzhan, HE Jianmin. Analysis of traction power supply system[M]. Chengdu: Southwest Jiaotong University Press, 2007: 70-101.

[17] 朱峰, 李嘉成, 李朋真, 等. 电气化铁路钢轨交流内阻抗计算[J]. 铁道学报, 2017, 39(12): 38-42. ZHU Feng, LI Jiacheng, LI Pengzhen, et al. Calculation of alternating-current impedance for the rail of electric railway[J]. Journal of the China Railway Society, 2017, 39(12): 38-42.

[18] Keshtkar H, Solanki S K, Solanki J M. Improving the accuracy of impedance calculation for distribution power system[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 570-579.

Research on calculation of rail self impedance of track circuit considering the influence of earth

ZHANG Youpeng, WANG Dong, ZHAO Bin, JIA Zhi

(School of Automation & Electrical Engineering, Lanzhou JiaotongUniversity, Lanzhou 730070, China)

The self impedance of the rail is one of the important parameters for the calculation and analysis of the track circuit, and its value directly affects the transmission performance of the track circuit. Considering the influence of the earth, it is difficult to determine the upper limit of the integral and the high frequency oscillation of the integrand function when the Carson formula is used to calculate the rail self impedance. A piecewise linear approximation method of Kernel function was proposed to solve the integrand function, and the truncation method was used to convert the infinite upper limit integral to the finite integral. The track circuit model was established and the finite element method was used for simulation calculation to verify the correctness of the calculation method. The calculation results of the method and Carson’s single approximation method were compared with the simulation results to verify the calculation accuracy of the method. The method was used to analyze the influence of current frequency, track height and ground conductivity on the rail self impedance. The research results show that the error between the calculation results of this method and the simulation results is less than 6%, the calculation accuracy is higher, and the influence of each parameter on the self impedance of the rail is correctly reflected. The results can provide reliable theoretical support for the accurate calculation of rail self impedance and the analysis of transmission characteristics of track circuit.

rail self impedance; Carson formula; Kernel function; piecewise linear approximation; truncation method; finite element method

U284.21

A

1672 - 7029(2020)11 -2929 - 09

10.19713/j.cnki.43-1423/u.T20200075

2020-01-23

国家自然科学基金资助项目(51967010)

张友鹏(1965-)，男，甘肃庆阳人，教授，从事电气化铁路牵引供电技术研究；E-mail：zhangyoupengypz@126.com

(编辑 阳丽霞)