人工配制盐渍土抗剪强度指标分布特征及变化规律研究★
2020-12-15付江涛孟宏睿陈丽红
付江涛 孟宏睿 陈丽红
(陕西理工大学土木工程与建筑学院,陕西 汉中 723000)
1 概述
为揭示盐渍土抗剪强度指标分布规律,对黄土中加入不等量Na2SO4的方法,制备不同含盐量的人工配制硫酸盐渍土,然后在上述基础上,对硫酸盐渍土开展剪切试验,确定其抗剪强度指标,最后采用分布估计和参数估计确定其服从的分布类型。本项研究成果对于盐渍土地区基础工程建设顺利开展和盐渍化对边坡稳定性影响评价,具有重要的理论研究价值和实际指导意义。
2 试验材料与方法
2.1 试样制备
将采集于试验区地表以下3 m处黄土试样碾散,将其置于温度为105 ℃的烘箱中烘烤24 h,过2 mm土工筛,将过筛的土体平铺于不吸水的铁质瓷盘中待用。由于硫酸盐渍土抗剪强度指标在低含盐量时(<3%)对含盐量变化较为敏感,故本项研究在试验设计时,将含盐量设定为0.0%,0.5%,1%,3%,6%,9%和12%等7个梯度。因区内土体天然密度实测值约为1.58 g/cm3,故本项研究中所设定土体密度亦为1.58 g/cm3,区内土体实测天然含水量为12.98%~19.6%,故本项研究土体含水量设定为12.0%。本项研究中人工配制盐渍土制备过程按照《土工试验技术手册程序》相关规定进行。此外,为了确保数据的可靠性和代表性,每组盐渍土设定12个平行试样,土体制备过程中,土样制备和试验均由同一人完成;待人工配制盐渍土制样结束后,将土样放入环刀盒中并用保鲜膜密封,再静置8 h进行养护,养护结束后即对土样开展直剪试验。
2.2 统计模型介绍
本文共采取了正态分布、伽马分布、泊松分布、瑞利分布、威布尔分布、中位秩公式对盐渍土抗剪强度进行了分析,上述模型可见文献[12][13]。
2.3 数据处理
为分析含盐量对土体抗剪强度指标显著性影响,本研究采用单因素方差分析(One-way ANOVA)及最小显著差异法(LSD),分别在0.05和0.01的水平上检验盐含量对人工配制盐渍土抗剪强度指标进行显著性和极显著性分析。方差分析及多重比较均通过基于统计理论的SPSS(13.0)完成,作图通过Matlab编程完成。
3 试验结果与分析
3.1 抗剪强度指标
由表1可知,对于盐渍土粘聚力,当含盐量为0.0%~12.0%时,粘聚力值为2.29 kPa~76.77 kPa,其变异系数最小值为17%,最大值为33%,相类似地,内摩擦角值则为20.30°~35.29°,其变异系数最小值为3%,最大值为9%,以上变异系数均大于陈立宏等(2005)[2]分析的小浪底库区心墙填筑土粘聚力值和内摩擦角值的变异系数(2%~13%),由此可见,不论是盐渍土粘聚力值还是内摩擦角值较普通土均表现出较大的离散性,故对其进行统计分析是十分必要的。
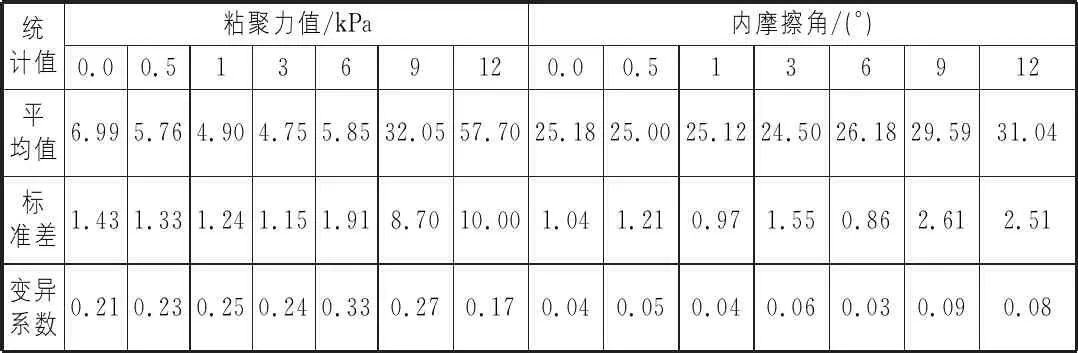
表1 人工配制盐渍土抗剪强度算数平均值及相关参数
3.2 盐渍土的粘聚力值分布特征
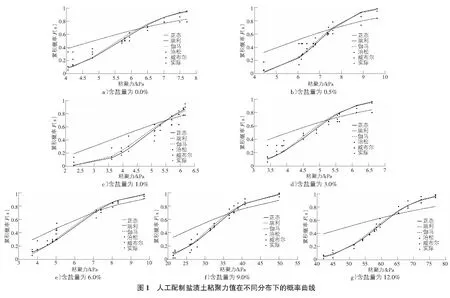
为定性分析本项研究中不同含盐量的盐渍土强度值所服从的分布函数,本项研究利用最大似然估计对表1中相关数据进行了估计,确定了在95%置信区间条件下,盐渍土在正态、伽马、瑞利、泊松和威布尔分布条件下的期望值和方差值,其结果如表2所示。将表2中的u及σ值代入正态分布、伽马分布、瑞利分布、泊松分布和威布尔分布的累计概率分布函数,即可获得7种含盐量盐渍土抗剪强度指标在不同分布下的概率曲线,如图1所示。由图1可知,对于任意一组盐渍土,5项概率分布中除泊松和瑞利分布外,其余3项分布概率理论曲线与其实际分布曲线均基本一致,如含盐量为0.5%时,盐渍土粘聚力值在正态、威布尔和伽马分布下的理论概率值与实际概率值的平均偏差值均为5%,而泊松和瑞利的理论概率值与实际概率值的平均偏差为0.13和0.16,如表3所示,上述结果表明,从定性的角度分析,7组盐渍土的粘聚力值分布比较符合正态、威布尔和伽马分布,而不符合泊松分布和瑞利分布。
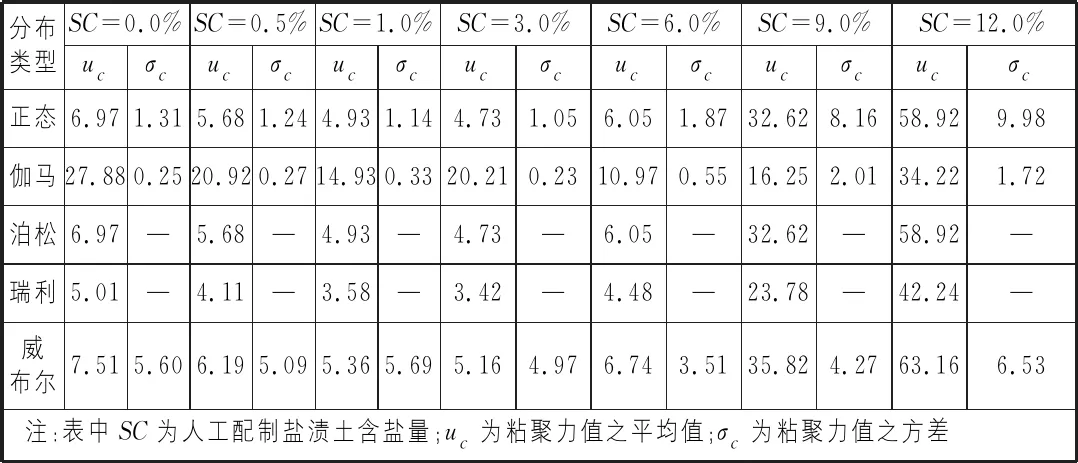
表2 人工配制盐渍土粘聚力值在不同分布下的参数
3.3 盐渍土内摩擦角值分布特征
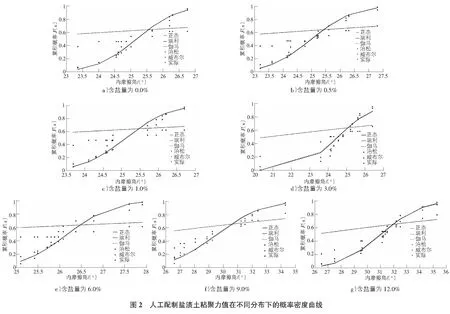
将表4所示的盐渍土内摩擦角相关参数uΦ及σΦ,代入正态分布、伽马分布、瑞利分布、泊松分布和威布尔分布的概率密度函数公式,即可获得7种含盐量的人工配制盐渍土的内摩擦角值在不同分布下的概率密度曲线,如图2所示。由图2可知,7组不同含盐量盐渍土内摩擦角值在正态、威布尔和伽马分布下的理论概率曲线与实际分布较为接近,如威布尔分布概率值与实际分布概率值平均偏差为0.03~0.09,正态分布概率值与实际分布概率值平均偏差为0.03~0.18,伽马分布概率值与实际分布概率值平均偏差为0.04~0.12,如表5所示。对表5进一步分析可知,盐渍土内摩擦角值在不同含盐量和不同分布下,其理论概率值与实际概率值平均偏差各不相同,如在含盐量为0.5%条件下,正态分布理论概率值与实际概率值平均偏差为0.03,而威布尔理论概率值与实际概率值平均偏差为0.05,而在含盐量为3.0%条件下,正态分布理论概率值与实际概率值平均偏差为0.06,威布尔理论概率值与实际概率值平均偏差则为0.03,该结果反映出在不同含盐量下,盐渍土内摩擦角值所服从的概率分布并不是唯一的,而是多元的[2]。
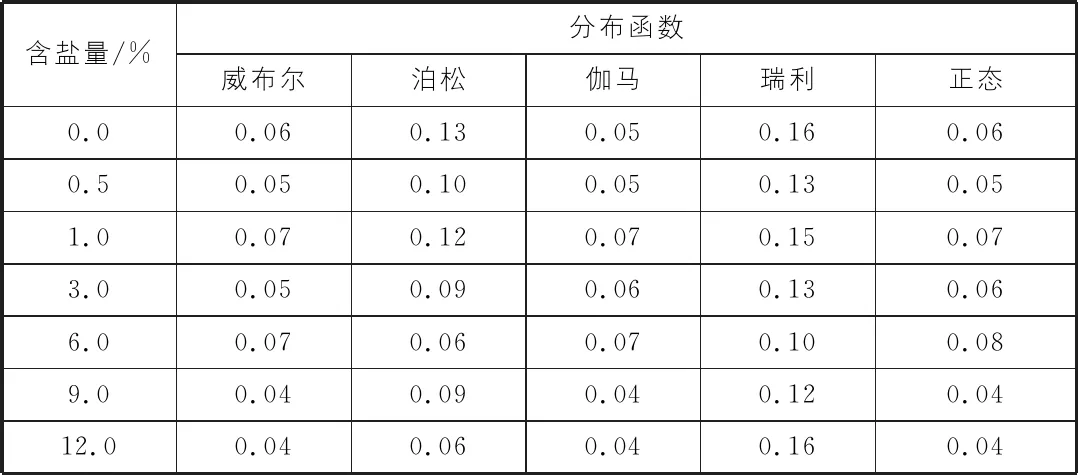
表3 盐渍土粘聚力值理论概率值与实际概率值偏差
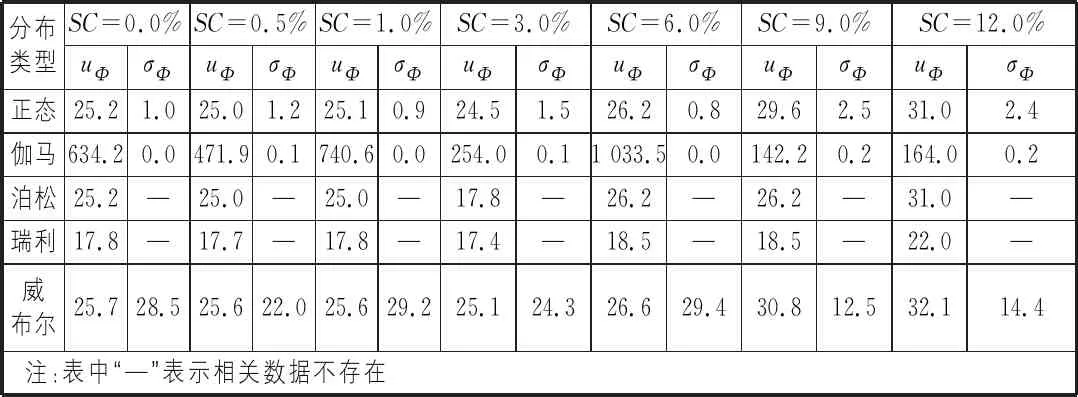
表4 人工配制盐渍土内摩擦角值在不同分布函数下的参数
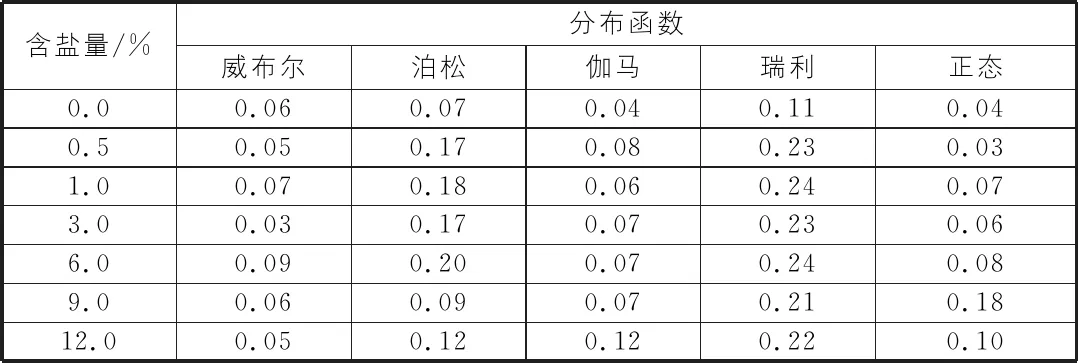
表5 盐渍土粘聚力值理论概率值与实际概率值偏差
3.4 抗剪强度指标与含盐量关系
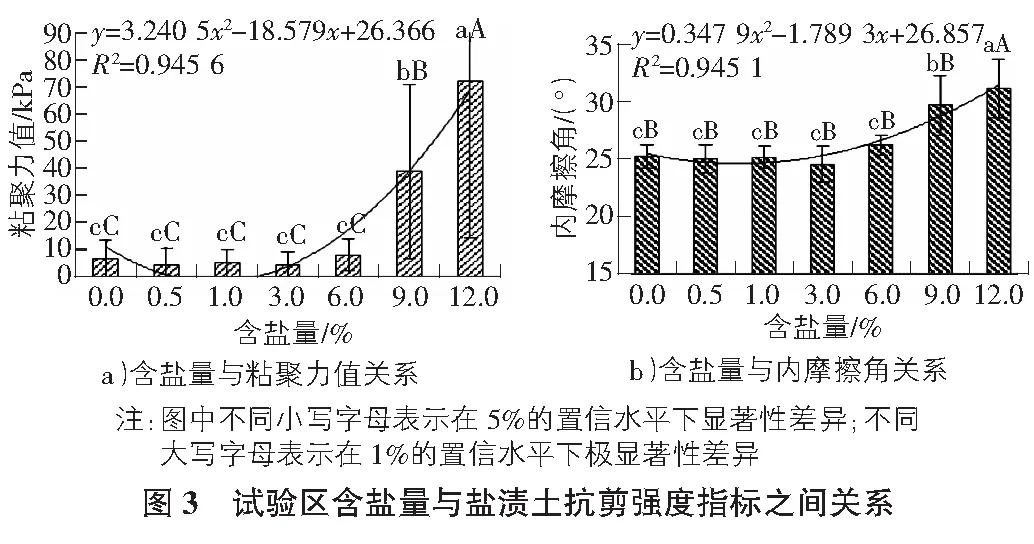
图3所示为人工配制盐渍土抗剪强度指标与含盐量关系,其中图3a)为粘聚力值与含盐量关系,由该图可知随含盐量单调增加,粘聚力值表现出先减小后增加的变化趋势,即由6.70 kPa递减至4.50 kPa,然后增加至72.30 kPa,且含粘聚力值最小值所对应的含盐量为3.0%;相类似地,人工配制盐渍土内摩擦角与含盐量亦表现出同样的关系,且其内摩擦角值最低值所对应的含盐量依然为3.0%,如图3b)所示,相类似的研究成果亦可见参考文献[14]。
4 结语
1)本项研究中,正态分布、威布尔分布和伽马分布函数均可用于拟合人工配制盐渍土粘聚力值的分布,而正态分布和威布尔分布则可适用于拟合人工配制盐渍土内摩擦角值分布。从拟合优度的角度分析,不同含盐量的盐渍土抗剪强度指标的最优分布函数随含盐量变化而变化,盐渍土粘聚力值在正态分布、威布尔分布和伽马分布函数下的理论概率与实际分布概率相差不大,而内摩擦角值在正态分布和威布尔分布的理论概率与实际分布概率相差不明显。
2)本项研究中,人工配制盐渍土抗剪强度指标随含盐量增加呈先减少后增加的变化特征,且抗剪强度指标最低值所对应的含盐量均为3.0%。
