基于遗传算法的水工钢闸门优化设计

2020-12-14王军钟亚丽于尧

人民黄河 2020年11期

王军钟亚丽于尧

摘要：针对水工钢闸门难以全局优化的现状，根据现行规范和水工钢结构设计理论，对水工钢闸门结构布置中的主梁根数及其高度、腹板厚度、上翼缘宽度和厚度、下翼缘宽度和厚度，以及面板厚度、横隔板根数、边柱腹板厚度、边柱翼缘宽度和厚度等12个独立形态参数，运用分流机制的新型遗传算法进行全局优化，初步实现了水工平面钢闸门的优化设计。实例应用表明，在一定的材料强度下，该方法只需在程序中输入孔口尺寸和上下游水位组合，经过优化，即可得到闸门自重最小值，从而降低闸门造价。如设定闸门自重不变，则通过优化可实现强度储备均匀，提高闸门的安全裕度。

关键词：水工钢闸门;全局优化;遗传算法;安全裕度

中图分类号：TV663.4 文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.11.019

Abstract： In view of the problem that hydraulic steel gates cannot be optimized globally， according to the design theory of hydraulic steel structures and current industrial standards， the number and height of the main beam， the width of web plates， the width and thickness of upper and lower flange of main beams， the thickness of panel， the number of diaphragms， the thickness of side column web plates， the width and thickness of side column flanges in hydraulic steel gates are discussed. A new genetic algorithm based on shunt mechanism was used to globally optimize the above 12 independent shape parameters. In this paper， the optimum design of hydraulic plane steel gate was preliminarily realized and the program had strong universality. The calculation of the example shows that the program only needs to be given the range of 12 independent body parameters （with certain combination of orifice sizes and the upstream and downstream water levels） and the optimum solution can be obtained by minimizing the weight objective function. This optimization method reduces cost and improves whole redundancy of the gate.

Key words： hydraulic steel gate; global optimization; genetic algorithm; redundancy

水工建筑物中鋼闸门通过关闭、开启或局部开启，可实现控制水位、调节流量等功能。闸门在工程费用中占比一般为20%[1]，对于平原地区低水头水工建筑物，其占比甚至达到50%，优化设计的经济效益较大。仇强等[2]利用遗传算法实现了平面钢闸门主梁设计的优化。许世刚等[3]运用一种基于分流机制的新型遗传算法对压板式短进水口进行优化，获得全局最优值，为闸门整体优化提供了思路。金菊良等[4]对基因算法进行了改进，改进后的基因加速法适应性更强、应用更广。李月伟等[5]基于CATIA V5软件平台，编制水工钢闸门设计系统计算模块，实现从工程可行性研究到实施全过程的可视化设计与管理。白润波等[6]对水工钢闸门轮轨接触强度的安定算法进行分析，基于安定极限荷载下限理论探讨轮轨的接触强度问题，建立自循环优化安定分析算法，并对90个不同状态下的轮轨接触强度进行了数值分析。刘云俊等[7]对在役水工钢闸门进行安全评估，通过蒙特卡罗抽样随机有限元分析，计算当前钢闸门主梁的可靠度指标，以此判定当前的钢闸门是否安全。王可等[8]利用CATIA软件开展水工钢闸门的三维设计，提出了一种新的“参数提交—设计计算—参数化快速建模—有限元分析校核—工程图优化调整”设计模式。

目前钢结构的应力计算分析理论日趋成熟，通过引入空间有限元分析方法，可以计入面板和水平次梁在闸门整体弯曲中所起的抗弯作用，较真实地反映闸门的工作情况，但需要事先人为拟定闸门的各部位尺寸，仅能起到强度复核的作用。水工钢闸门优化设计中约束条件非常复杂，以往的方法在钢闸门设计中应用困难较大，随着现代优化理论的发展及计算机运算速度的提高，现在可以对钢闸门优化设计进行新的尝试。遗传算法（GA）是一种仿生类算法，它以自然进化和遗传变异理论为基础，多用于复杂问题的优化分析，在所有的工程和科学问题中几乎都有应用[9-10]。

钢闸门属于空间受力体系，目前常拆分为平面体系，按结构力学的方法进行受力分析。对于中小型闸门来说，可直接采用平面体系分析的结果，《水利水电工程钢闸门设计规范》[11]也推荐该方法，对于大型工程，可以其优化结果为基础，再进行精确的有限元分析。

水工钢闸门门叶一般由面板、主次梁、联结系、支承及止水等部件组成，从传力路径看，水压力通过面板、次梁、主梁、边柱、行走支承、闸门埋固件依次传递到闸身或坝体[12-13]，而闸门联结系多为构造要求。钢闸门优化设计一般指面板、主次梁、边柱的布置及结构尺寸的优化，需要寻找一种适当的优化方法，从无数种组合中得到经济合理的方案。笔者根据现行规范[11-12]，按照目前通用的水工钢结构设计理论，应用MATLAB语言编程，运用遗传算法初步实现了水工平面钢闸门的全局优化。

1 水工钢闸门优化设计数学模型

本次水工钢闸门优化，外部参数仅包括孔口的净宽、净高及上下游水头，与闸门有关的其余尺寸均作为独立的变量进行优化。

水工钢闸门优化是有约束条件的非线性规划问题，包括设计变量、目标函数和约束条件三个内容。

1.1 设计变量

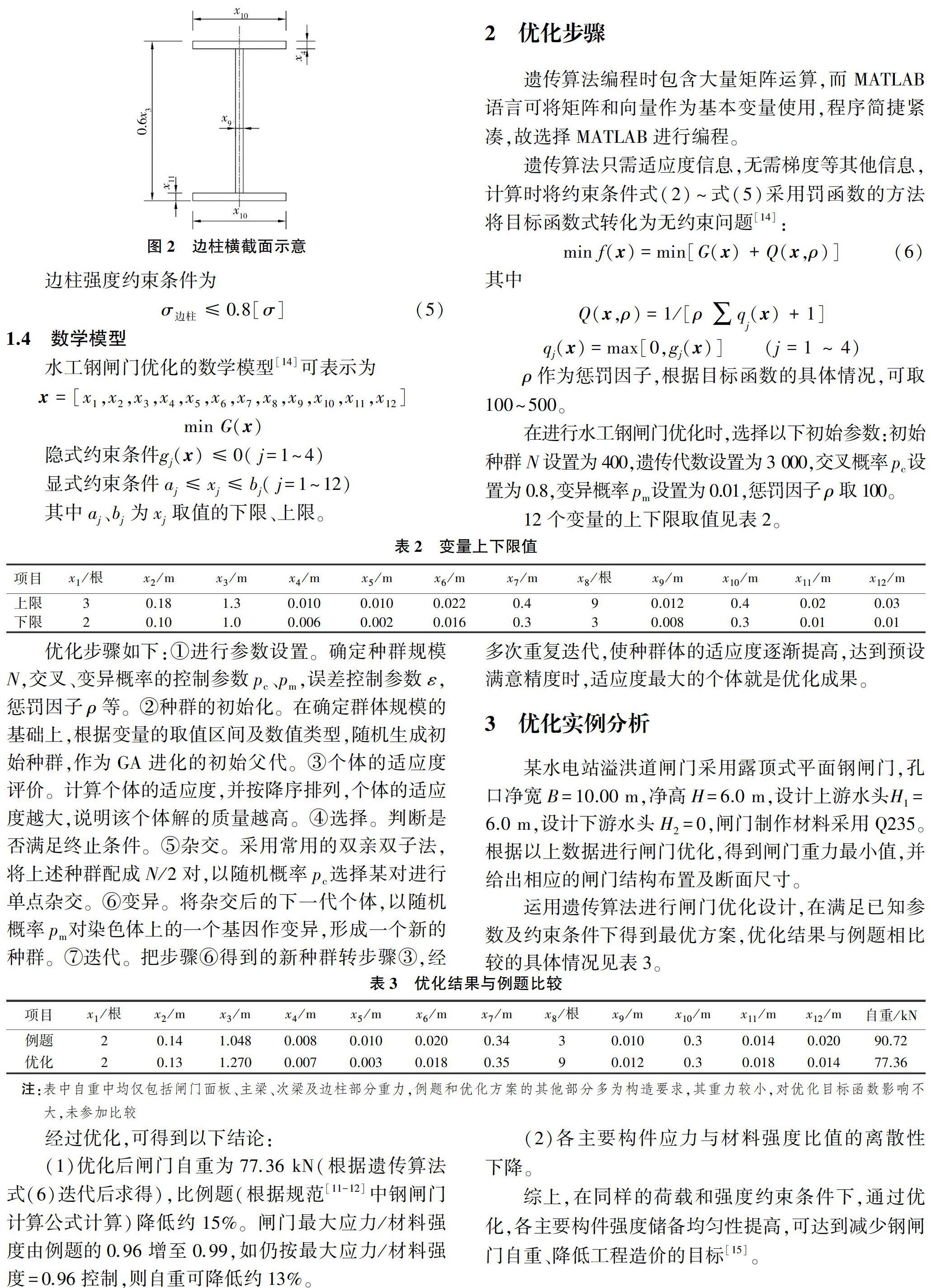
设计变量包括已知参数和待优化变量两部分，闸门设计时，已知参数有5个，分别为上游侧水头H1、下游侧水头H2、闸孔净宽B、闸孔净高度H、材料强度[σ]。待优化变量是与闸门结构设计有关的12个相互独立的体形参数，具体见表1。

优化步骤如下：①进行参数设置。确定种群规模N，交叉、变异概率的控制参数pc、pm，误差控制参数ε，惩罚因子ρ等。②种群的初始化。在确定群体规模的基础上，根据变量的取值区间及数值类型，随机生成初始种群，作为GA进化的初始父代。③个体的适应度评价。计算个体的适应度，并按降序排列，个体的适应度越大，说明该个体解的质量越高。④选择。判断是否满足终止条件。⑤杂交。采用常用的双亲双子法，将上述种群配成N/2对，以随机概率pc选择某对进行单点杂交。⑥变异。将杂交后的下一代个体，以随机概率pm对染色体上的一个基因作变异，形成一个新的种群。⑦迭代。把步骤⑥得到的新种群转步骤③，经多次重复迭代，使种群体的适应度逐渐提高，达到预设满意精度时，适应度最大的个体就是优化成果。

3 优化实例分析

某水电站溢洪道闸门采用露顶式平面钢闸门，孔口净宽B=10.00 m，净高H=6.0 m，设计上游水头H1=6.0 m，设计下游水头H2=0，闸门制作材料采用Q235。根据以上数据进行闸门优化，得到闸门重力最小值，并给出相应的闸门结构布置及断面尺寸。

运用遗传算法进行闸门优化设计，在满足已知参数及约束条件下得到最优方案，优化结果与例题相比较的具体情况见表3。

经过优化，可得到以下结论：

（1）优化后闸门自重为77.36 kN（根据遗传算法式（6）迭代后求得），比例题（根据规范[11-12]中钢闸门计算公式计算）降低约15%。闸门最大应力/材料强度由例题的0.96增至0.99，如仍按最大应力/材料强度=0.96控制，则自重可降低约13%。

（2）各主要构件应力与材料强度比值的离散性下降。

综上，在同样的荷载和强度约束条件下，通过优化，各主要构件强度储备均匀性提高，可达到减少钢闸门自重、降低工程造价的目标[15]。

4 结论

本文研究了水工钢闸门的受力机理，运用遗传算法进行优化计算，将优化计算成果直接导入水工钢闸门绘图软件，可实现钢闸门的自动化设计，大幅提高钢闸门设计效率。平面钢闸门优化的技术思路也可用于弧形钢闸门以及人字闸门。通过优化门体结构布置，各部位强度储备趋于一致，可体现结构优化理论中均匀强度的特点。在同样的荷载和强度约束条件下，闸门自重可减小，投资降低;对于具体的工程项目来说，可在闸门自重不变的前提下，使各部位强度储备均匀、最大应力降低，闸门的安全度显著提高。

参考文献：

[1] 安徽省水利局勘测设计院.水工钢闸门设计[M].北京：水利电力出版社，1980：1-8.

[2] 仇强，秦斌，侯作启，等.遗传算法在平板钢闸门优化设计中的应用[J].人民黄河，2010，32（1）：128-129.

[3] 许世刚，王军.一种新型遗传算法在水力优化设计中的应用[J].水电能源科学，2002，20（1）：35-37.

[4] 金菊良，杨晓华，储开凤，等.加速基因算法及其在水库计算中的应用[J].水电能源科学，1997，15（3）：57-60.

[5] 李月伟，陈智海，齐文强.水工钢闸门设计系统计算模块的编制[J].人民长江，2016，47（1）：48-49，55.

[6] 白润波，曹平周，CAO M S.水工钢闸门轮轨接触强度的安定算法分析[J].人民长江，2009，40（9）：39-43.

[7] 刘云俊，杨建明，叶小强.基于检测数据的在役水工钢闸门主梁可靠度分析[J].人民长江，2010，41（17）：88-91.

[8] 王可，陈智海，王蒂，等.基于CATIA的钢闸门参数化建模技术研究[J].人民长江，2016，47（2）：32-35，41.

[9] 马光文，王黎.水火电力系统优化调度的逐步最优遗传算法[J].水电能源科学，2000，18（2）：69-72.

[10] 邢文训，谢金星.最优化基础-模型与方法.现代优化计算方法[M].北京：清华大学出版社，1999：113-147.

[11] 中华人民共和国水利部.水利水电工程钢闸门设计规范：SL74—2019[S].北京：中国水利水电出版社标准化出版分社，2019：1-18.