研究“草图”，探究“内理”

赵静 张建国

【摘要】借助“草图”可以帮助学生把复杂的数学问题变得简明、直观，有助于学生寻求解决问题的思路，估计出结果。借助“草图”不仅有利于学生实现思维从形象到抽象的跨越，而且能为以后提高空间想象能力积累丰富的经验。

【关键词】草图   抽象  直观   理解

数学家阿蒂亚曾提出，视觉思维占主导地位。在小学阶段，学生以形象思维为主，用形象思维观察问题、分析问题、解决问题。引导学生学会借助草图来理解数学问题，是数学教学中落实几何直观的具体体现。借助草图可以培养学生的一种思维方式，有利于学生直观、巧妙地找到解决问题的突破口，深入理解数学问题，使学生的思维转向更抽象、更高级的空间形式，有助于学生形成良好的思维品质。

一、借助“草图”理解数学概念

【片段1】1公顷的[3] [4]和3公顷的[1] [4]

师：你们知道1公顷的[3] [4]和3公顷的[1] [4]分别是多少公顷吗？

生：都是[3] [4]公顷。

师：你是怎么来理解的？

生1：我是画图来理解的。

生2：我是计算得来的。求一个数的几分之几是多少，用乘法计算。结果都是[3] [4]公顷。

阿提雅说过：“几何直观是领悟数学最有效的渠道。”借助草图可以把抽象的数学问题直观地呈现在学生面前，有助于学生对数学知识的理解，培养学生的数学直觉;借助草图可以来验证计算结果，促进学生对计算结果的理解，培养学生对数学结果的判断力。根据题意画草图，是学生学习过程中最常用的一種方法，一种解题技能，也是学生对数形结合思想的一种体验。我们要让学生体会到画草图的价值，体会画草图是理解问题、解决问题的一种策略。

二、借助“草图”理解计算算理

【片段2】分数与分数相乘

要求：请涂色表示出长方形的[3] [4]。（出示两个同样大小的长方形图）

学生确认后，画出阴影。

师：阴影部分占长方形的几分之几？

生：[3] [4]。

师：那阴影部分的二分之一该怎么表示呢？它又是长方形的几分之几呢？

（生画一画）

师：[3] [4]的[1] [2]是多少？

师：能看图列算式填写结果吗？

……

在图中表示出：[4] [5]的[2] [3]是多少？[4] [5]的[1] [2]是多少？

计算对于学生来说最难理解的是算理，尤其是分数乘分数的计算，学生理解起来更是难上加难，用草图直观地展示在学生面前整个计算过程，并直观地在图中显现出结果，让学生清晰地沟通了算理和算法之间的联系。在片段2中，借助长方形图帮助学生理解分数乘法的意义，同时也借助了长方形草图验证了分数乘分数的结果，并能让学生理解归纳出算法。刘加霞博士指出：经验的获得需要“领悟”与“转化”。学生通过视觉观察或参与具体活动，可以直接获得具体经验;再通过回顾、反思所经历的活动，进行内在的思考，不断内化为能够理解的、抽象的、合理的经验;最终在解决新问题的过程中证实和运用获得的经验，从而不断创生出新的经验。

三、借助“草图”解决实际问题

【片段3】有关电线长度计算的实际问题

出示例题：一根电线截去[1] [4]后再接上12米，结果比原来长[1] [3]。这根电线原长多少米？

像此类解决问题，如果学生不画草图，恐怕很难理解，也很难解决。如果把草图画出来，学生看了草图后就很容易迎刃而解。

画出线段图后，学生结合图形就能看出一根电线的[1] [4]和这根电线的[1] [3]加起来的长度就是12米。根据线段图找到这样的等量关系，就很容易列算式

解答了。

在解决问题的过程中，理清数量关系是核心，任何一个数学问题都是由情境和数量关系两部分组成的。寻求问题的结果，取决于对情境的理解，理清数量关系，从而建立求解模型。大多数学生喜欢形象思维，抽象思维的能力还有待发展，因此极少有学生会主动借助草图来寻找问题的突破口。如果学生能养成画草图的习惯，这样的草图可以是线段图，可以是方块图，等等，只要能化抽象为直观，帮助理解和思考的草图都可以尝试。运用草图不仅能比较容易找到解题思路，还能进一步提升思维的深度。上面有关电线长度的计算题，数量关系混乱，很难找到等量关系入手，让学生画线段图，结合草图，就很容易看出分数和对应数量之间的关系。“直观与推理是图形与几何学习中的两个重要方面”。在小学数学教学中，借助草图有利于学生理解抽象的概念、法则等，有利于学生解决一些稍复杂的实际问题，从而培养学生的空间想象能力，提升学生的数学思维水平，进一步激发学生数学学习的兴趣。

四、借助“草图”理解数学结果

【片段4】最多可以剪多少个直角三角形

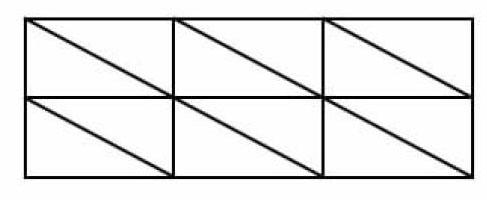
出示例题：在长12分米、宽6分米的长方形布上剪直角边长分别为3分米和4分米的直角三角形，最多可以剪多少个？

师：请同学们在长方形图里动手画一画。

师：通过画一画，你发现了什么？

生：我们可以先剪长4分米、宽3分米的长方形，最后把长方形分成两个直角三角形。

师：那这样的长方形最多可以剪多少个呢？

生：我们可以看大长方形的长里面可以剪多少个这样的小长方形，宽里面可以剪几排这样的小长方形。（生借助图向大家介绍）

师：能用算式表示出来吗？

生：12÷4=3（个），6÷3=2（排），3×2=6（个）可以剪6个长方形。而每个长方形可以剪成两个完全相等的直角三角形，所以一共可以剪12个这样的三角形。

师：从图上看，正好剪完，没有剩余。非常好。我们可以看长里面可以剪多少个，宽里面可以剪多少排？那如果不能正巧剪完，又该怎么办呢？

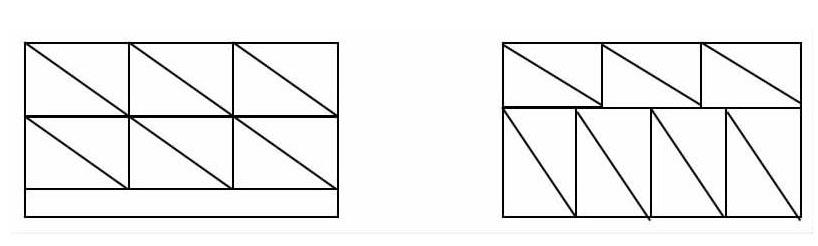
出示例题：在长12分米、宽7分米的长方形纸上剪直角边长分别为3分米和4分米的直角三角形，最多可以剪多少个这样的直角三角形？

师：也请同学们在长方形图里动手画一画。

（生展示了两种不同的图）

师：请同学们观察这两种剪法，你们觉得最多可以剪多少个这样的直角三角形？

生：14个。

小学生的思维通常以直观、形象为主，他们的空间想象能力容易受到阻碍，因此往往有些学生会有思维定式，停留在同种类型的解题模式上，而不能理解问题的内理，掌握问题的本质。动手画一画草图，借助直观的图形，可以帮助学生理清问题的本质，得出问题的结果。在以上教学片段中，教师让学生动手画一画，思考剪长4分米、宽3分米的长方形，最多可以剪多少个？这时长和宽都能正好剪完，通过图来验证结果，一目了然。然而，教师又出了一道不能正好剪完的题，此时最多又能剪多少个呢？有的学生还是用了原来的方法，有些学生则通过画图剪出了更多三角形。学生借助草图，有效地将抽象的数学结果形象化、简单化，进一步理解在遇到此类问题时应如何分析和解决。

【参考文献】

[1]贲友林.此岸与彼岸Ⅱ[M].南京：江苏凤凰教育出版社，2015.

[2]曹培英.跨出断层，走出误区：“数学课程标准”核心词的实践解读之四——几何直观[J].小学数学教师，2013（6）.

[3]陈荣芳.适切引导，有机渗透——例谈低年级学生画图策略意识的培养[J].小学教学研究，2014（12）.