简便意识：小学生数学数感培养的重要途径

缪建平

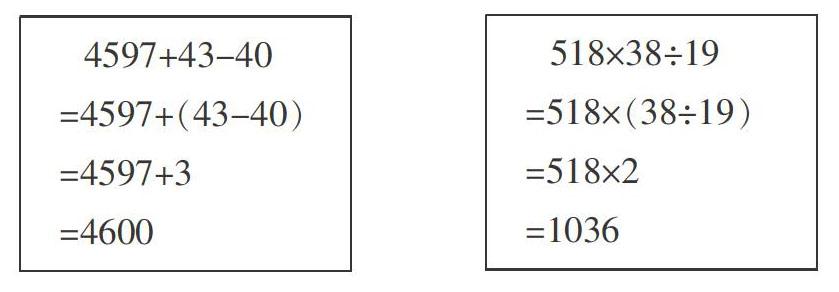
【摘要】“简便意识”是“数感”的一种重要表现形式。“简便意识”即简便运算的意识，是指学生在掌握一定的计算知识与技能的同时，自发运用运算定律（性质、规律等），达到计算的最优化，使计算变得简捷的心理意向。通过认知心理学、日常调查和观察分析，我们发现学生缺乏简便意识，本文逐一进行了分析，并给出了教学建议。

【关键词】简便意识   数感   原因分析   培养   刍议

人们在学习和生活实践中，经常要和各种各样的数打交道。如果学生能有意识地将一些事物、现象与数、数量建立联系，自觉、主动甚至自动化地运用数学眼光、数学态度、数学思想去理解和把握生活实际中的数学现象，并运用适切的数学方法和策略去解决生活中的实际问题，就是其具有“数感”的具体表现。

数感是人的最基本的数学素养，英文为“Number Sense”，可翻译成数感、数觉或数意识。在《义务教育数学课程标准（2011年版）》中，“数感”被作为十大核心概念之一被提出，进一步说明它在数学素养中的重要地位。

应该说，“简便意识”是“数感”的一种重要表现形式。“简便意识”即简便运算的意识，是指学生在掌握一定的计算知识与技能的同时，自发运用运算定律（性质、规律等），达到计算的最优化，使计算变得简捷的心理意向。具有“简便意识”的学生，能在进行四则运算及相关实际应用问题时，有意识地观察所要解决的问题，敏锐地发现其中数与数之间的关系，并且自觉地让数与数之间发生巧妙的联系，找到最简便合适的运算方法，进而顺利快捷地解决问题，并产生愉悦的成功体验和审美体验。

然而，我们在日常教学中，不难发现下列两种现象。一种现象是学生对要求“简便运算”的计算题算得正确、合理、熟练，但有时却把不能进行简便运算的计算题也“硬去简便”造成了错误;另一种现象是，在其他不要求进行“简便计算”的日常解题或运算中，尽管题目可以简便运算，却因学生缺乏自觉简便的意识，不能灵活处理，从而表现出某种习惯心理或惰性心理。

比如，学生在刚学习了运用运算律进行简便运算后，碰到诸如“34×43+12×23”这样的题目时，苦思冥想，想套用“某某运算律”来进行简便运算。

再比如，在计算铜管（见图1）的体积时，由于学生缺乏简便意识，不能主动发掘题目中的隐蔽的信息及其之间的联系，最终陷入烦琐的计算中，造成列式正确但往往不能计算出正确结果的“怪现象”。

学生的“简便意识”哪儿去了？为什么学生缺乏自觉进行简便运算的意识呢？通过学习认知心理学理论、日常调查与观察分析，发现有如下原因。

一、思维定式消极影响

思维具有方向性，思维的定势是人人都有的。思维定式既有积极的一面，也有消极的一面。当学生学习新知识时，就需要利用类似的旧知的定势来形成和巩固所学的新知识;而当学生已经掌握了该知识，如果仍然用类似的旧知識去强化定势，使某一知识方法处于统治地位，学生囿于某一方法，就会表现出思维的惰性。相反，如果教师注意到这种消极影响，经常采用“突变题”予以打破，往往能收到较好的教学效果。

比如，在教学低年级加减两步计算及乘除两步计算时中，教师经常设计诸如6-8+4、34-18-2、6×2×5（表内乘法）、8×6÷3（表内乘除）的题目，让学生进行练习，就一定能突破“运算从左到右”的思维框架，也为学生以后进一步学习四则运算养成良好的思维习惯打下了坚实的基础。

教师在进一步让学生计算“4597+43-40”“518×38÷19”时，学生似乎从中观察到一些数学之间的关联，分别计算如下：

二、思维发散不够流畅

美国心理学家吉尔福特提出：人类智力是由操作、内容、产品三个维度组成的结构模型。在操作这一维度上，他提出了由认知、记忆、发散性思维、辐合性思维和评价五个方面。他明确地把“发散性思维”定义为一个不依赖常规、寻求变异、从多方面寻求答案的思维方式，并把思维的流畅性作为发散思维的一个基本要求。

运算中受思维习惯心理影响较大的学生，思维的流畅性如何呢？我们曾做过一个小实验：比较大小，用“>”连接以下各分数：[15] [22]、[10] [17]、[40] [37]、[12] [19]、[30] [41]。

结果只有10%左右的学生，在三分钟以内给出了这道题的正确答案。他们摒弃了常规思维下的比较分数大小的方法（通分），创造性地用求各分子的最小公倍数的方法来比较大小。显然，大多数学生的思维流畅性不及这10%的学生。

训练和培养学生思维的流畅性的一般策略是：（1）要求学生对一些常用的方法提出新的或非常用方法;（2）在非评价气氛下进行快速联想训练，以鼓励学生就事物进行信息转换。

三、信息加工缺乏深度

心理学认为，解决问题要靠知识，而知识以模式为导引。有经验的人能够较快地从问题中把他原来熟练的模式辨别出来，然后进行问题解决。可以认为，模式辨认是决定问题解决的关键所在。如果问题简单，模式辨认一般没有什么困难;如果问题复杂，辨认就比较困难了。

比如，刚刚上面举到的“计算铜管的体积”这一问题，还有下面的求复杂几何图形面积的问题（见图2）。

如果不能对信息进行深度加工，学生就会陷入烦琐的计算中。因此，教师要善于引导学生发掘题目中隐藏的信息，主动地对问题进行有效加工，而不是停留在一般感知层面，这样就能顺利而简捷地进行解答。

比如，在图2中，教师在平时教学中就要引导学生进行初步建模：每个空白部分占正方形面积的21.5%。于是，阴影部分面积=正方形面积×（1-21.5%×2）=6×6×57%=20.52（平方厘米）。

教学中，教师经过多次地指导及强化后，学生不但能形成有关几何形体计算的一般性策略，而且有利于培养学生排除无关信息干扰，主动加工，并迅速进行模式辨认与自觉简算的能力。

四、缺乏策略评价意识

“策略评价”是解决问题能力表现的一个重要方面。学生缺乏简便运算意识的一个重要表现就是缺乏对策略评价的意识，“不怕计算麻烦”是缺乏策略评价意识的学生的共同特点。在做题时，有的学生往往是找到一种方法就心满意足，即使是很复杂的运算，也没有去想一想“有没有简便的算法”的化归思想，而是硬着头皮继续“死算”下去。

这种现象不能责怪学生，我们应从教学内容组织和教师教学引导两方面去找原因。一方面现行课程内容中引发学生策略评价的方面做得还不够，抑或是教师在组织教学内容时没有有意识整合这一方面的内容，课本中似乎用一句“能简便时就简便”打发学生了事。另一方面，教师也怕学生在简便运算的过程中发生错误，于是只要求学生算对就行，并没有强行要求学生要有简便意识。

解铃还须系铃人。首先教师本身就需要有自觉的策略评价意识，其次还要把这样策略评价意识传递给学生。这就要求教师在日常教学中，通过一个个鲜活的教学实例，让学生逐步明白：日常数学学习中，无论是解答什么类型的数学题，不管有无简算指令，只要具备合理而简便的运算条件的，都要自觉地、有意识地按最简捷方法进行解答。同时，教师还可结合数学活动课，讲讲诸如数学家高斯的小故事、精选介绍课外书的“巧算与妙算”的方法、向学生们推荐阅读《算得快》《算得巧》等数学读物，这样，可以拓宽学生的数学认知领域，使其速算巧算策略得到了积累，反省评价意识也得到了增强，简便意识也就会慢慢地增强。