基于神经网络的水库枯季中长期径流预测模型研究
2020-12-14柏平
柏 平
(重庆市水利电力建筑勘测设计研究院,重庆 400020)
我国水资源短缺已是国内公认急需解决的突出问题,尤其是在枯水季,由于来水量较低,在一定程度上降低了河流的自净能力,水污染十分严重,因此在枯水季水资源供需矛盾问题尤为突出,对径流进行预报是解决这一问题的有效途径之一[1- 3]。目前针对径流预报的方法主要包括时间序列法[4]、多元线性回归法[5]、组合回归法[6]等,这些方法操作简单,在一定条件下可对径流进行模拟,但由于要求的条件过高,导致精度无法满足日常工作的需要。Schreiber和Demcth[7]在1997年基于河流网络法对水库径流进行了预报,在当时取得了较高的精度,但该方法需对河流进行网格划分,计算步骤较复杂;Rifai[8]总结了影响枯水季径流的因素,并基于此对枯水季径流进行了预报,指出下垫面因素是影响枯水季径流的主要因素。
随着人工智能算法的引进,神经网络模型逐渐被应用于径流预报当中。神经网络模型由输入层、隐含层和输出层几部分组成,可模仿人脑神经结构构建复杂的数学网络模型,可根据已输入的数据进行训练,找出数据内在规律,对径流数据进行预测[9- 10]。何国栋等[11]基于优化的RF及SVM的组合模型建立了径流预测模型,指出该模型对数据训练、检验和预测的平均相对误差分别为2.76%、4.64%、3.02%,精度较高;李文敬等[12]基于IQPSO优化SVM模型构建了径流预测模型,指出该算法能够有效提高月径流预报精度;岳兆新等[13]基于改进深度信念网络模型构建了中长期径流预测模型,并与传统的MLR和ARIMA模型进行对比,指出神经网络模型精度显著高于传统模型。
由于枯水季径流较少,水资源矛盾尤为突出,本文拟基于实测枯水期径流数据,基于前馈神经网络FN、动态递归神经网络EN、卷积神经网络 RBF、级联神经网络CN共4种神经网络模型,构建枯水期径流预报模型,为枯水期中长期径流预报提供基础。
1 研究方法
1.1 前馈神经网络
该模型是结构较简单的神经网络模型,主要包括正向传播和反向传播2个部分。模型主要结构包括输入层、隐含层和输出层3个部分,首先输入的数据由输入层开始正向传播,经隐含层运算后由输出层输出,如果输出的结果无法满足要求,模型自动进入反向传播结构,进而进一步减小运算误差,直到输出结果满足要求为止[14]。模型结构如图1所示。

图1 前馈神经网络模型原理图
1.2 动态递归神经网络
该模型在前馈神经网络的基础上,引入时滞计算因子,可根据数据的时间变化规律,适应时变特性,进而增加模型的稳定性和精度,具体结构如图2所示,该模型相较于前馈神经网络模型,增加了承接层,可方便数据的获取及筛选。

图2 动态递归神经网络原理图
1.3 卷积神经网络
卷积神经网络模型由卷积层和池化层组成,2种结构层交替出现,通过提取前一层的特征值,与后一层的神经元相连接,神经网络的卷积运算是通过稀疏连接、参数共享、等变表示的重要特性来改进学习训练系统,模型具体计算步骤可参考文献[15]。
1.4 级联神经网络
将BP神经网络作为前级网络,RBF神经网络作为后级,充分结合2种模型的优点,建立级联神经网络模型,以BP神经网络模型的输入结构作为输入层,RBF神经网络作为计算层和输出层,建立枯水季径流中长期预报模型。
1.5 模型训练与预测
4种神经网络预测模型分别采用5种训练算法进行训练,分别为梯度下降法traingd、有动量的梯度下降法traingdm、自适应 lr 梯度下降法traingda、贝叶斯正则化算法trainbr、一步正割算法trainosss,共建立20种神经网络模型用于构建枯水季径流预测模型。
1.6 模型精度验证
模型计算精度指标可采用以均方根误差(RMSE),相对均方根误差(RRMSE),确定系数(R2),纳什系数(NS)和效率系数(Ens)5种指标形成评价指标体系来评判不同模型的精度,具体公式如下:
(1)
(2)
(3)
(4)
(5)

由于评估指标过多,单个评估指标很难比较不同的模型。因此,引入GPI指数来全面评估模型仿真结果,公式如下:
(6)
式中,αj—常数,RMSE和RRMSE取1,NS取-1;gj—不同指标缩放值的中位数;yij—不同指标的尺度值。
2 结果分析
2.1 模型基本参数确定
选取了不同隐含层节点个数下对模型基本性能的影响,结果如图3所示。由图3可以看出,不同隐含层节点数对模型精度的影响不同,其中模型误差随着隐含层节点数的增加,呈现先降低后升高的趋势,这表明隐含层节点数需选取合适的范围,过高的节点数有可能增加模型误差,当隐含层节点数为10时,模型误差最低,精度最高,同时模型运行时间较短,仅有23.74s。同时由图3可以看出,神经网络模型最大迭代次数可达4500次,因此,神经网络模型所选取的最优隐含层节点数为10,设置模型最大迭代次数为4500,可保证神经网络模型精度最高。
2.2 模型最优训练算法确定
分别选取不同训练算法,研究不同训练算法下20种不同神经网络模型的运行速度,选取最优训练算法进行径流模拟,结果见表1。通过分析发现,traingd、traingdm、traingda、trainbr 4种训练算法在不同模型中,均出现了运行速度较慢的情况,而trainosss算法在4种神经网络模型中,均保持了较快的运行速度,可用于径流预测。

表1 不同训练算法运行效率对比
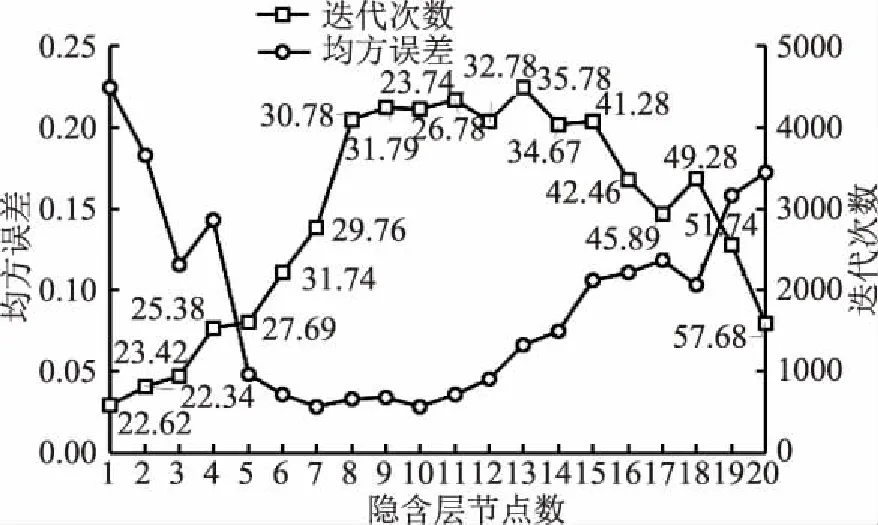
图3 模型基本性能与节点数关系
2.3 枯水季不同月份径流模拟结果对比
图4为不同模型在枯水季不同月份的径流模拟结果。由图4可以看出,不同模型模拟结果的变化趋势与实测值基本一致。10月—次年3月,级联神经网络CN模型的模拟精度最高,与实测值的平均相对误差仅为10.3%~14.1%,而前馈神经网络FN模型的精度最低,相对误差为41.5%~46.8%。
2.4 枯水季不同月份径流模拟结果精度对比
表2为不同模型模拟结果的精度指标计算结果。由表2可以看出,在10月,CN模型模拟精度最高,RBF精度次之,RMSE分别为1.982和2.049m3/s,RRMSE分别为14.6%和15.1%,R2分别为0.934和0.929,Ens分别为0.933和0.928,NS分别为0.942和0.931,GPI分别为1.661和1.578,在4个模型中排名前2位;在11月,CN模型精度最高,而FN模型精度最低,其RMSE高达5.697m3/s,RRMSE为40.1%,R2、Ens、NS分别为0.440、0.421和0.442,GPI仅为-3.565,排名最低;在其余月份,4种模型精度均表现为CN模型>RBF模型>EN模型>FN模型,综上所述,级联神经网络模型在枯水季径流模拟中的精度最高。
3 结论
本文基于4种神经网络模型5种训练算法共20种模型,分别构建了枯水季径流预测模型,并与实测径流进行了对比,确定了模型最优参数,得出以下结论。
(1)模型基本参数选取不同时,将使模型表现出不同的精度,模型最优隐含层个数可取10,迭代次数可取4500,可使模型精度最高且运行效率最高。
(2)不同训练算法下的模型运行效率不同,当采用一步正割trainosss算法时,可保证4种神经网络模型均具有较高的运行效率。
(3)对枯水季10月—次年3月的径流进行模拟可知,级联神经网络模型的精度最高,可作为枯水季径流预测的标准模型使用。
(4)本文仅基于神经网络模型构建了水库枯水季径流预测模型,在今后的研究中,可同样基于神经网络模型构建水库丰水季径流预测及全年径流预测模型,进一步探明级联神经网络模型的适用性。
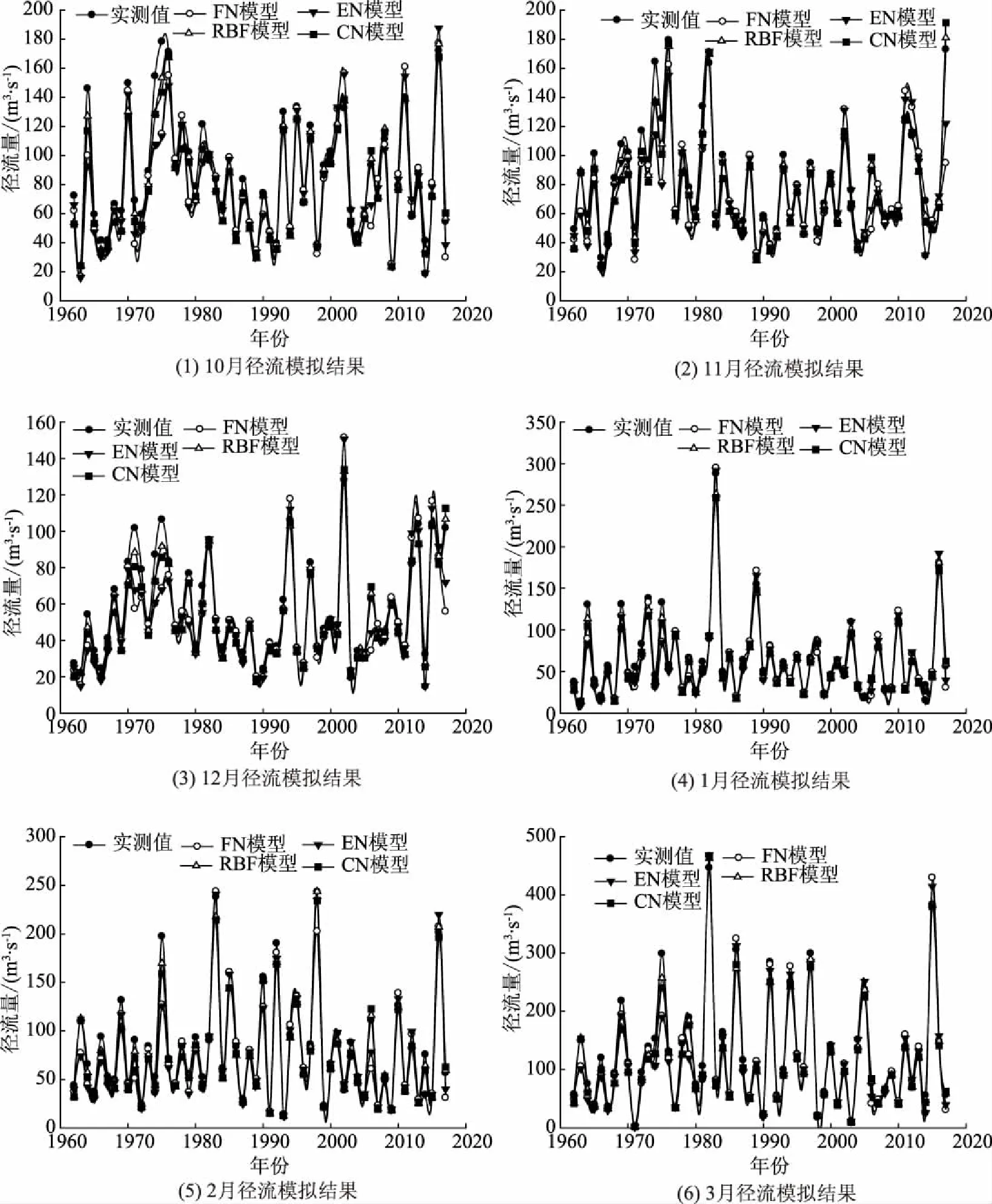
图4 枯水期不同月份不同模型径流模拟结果对比

表2 不同模型模拟精度对比
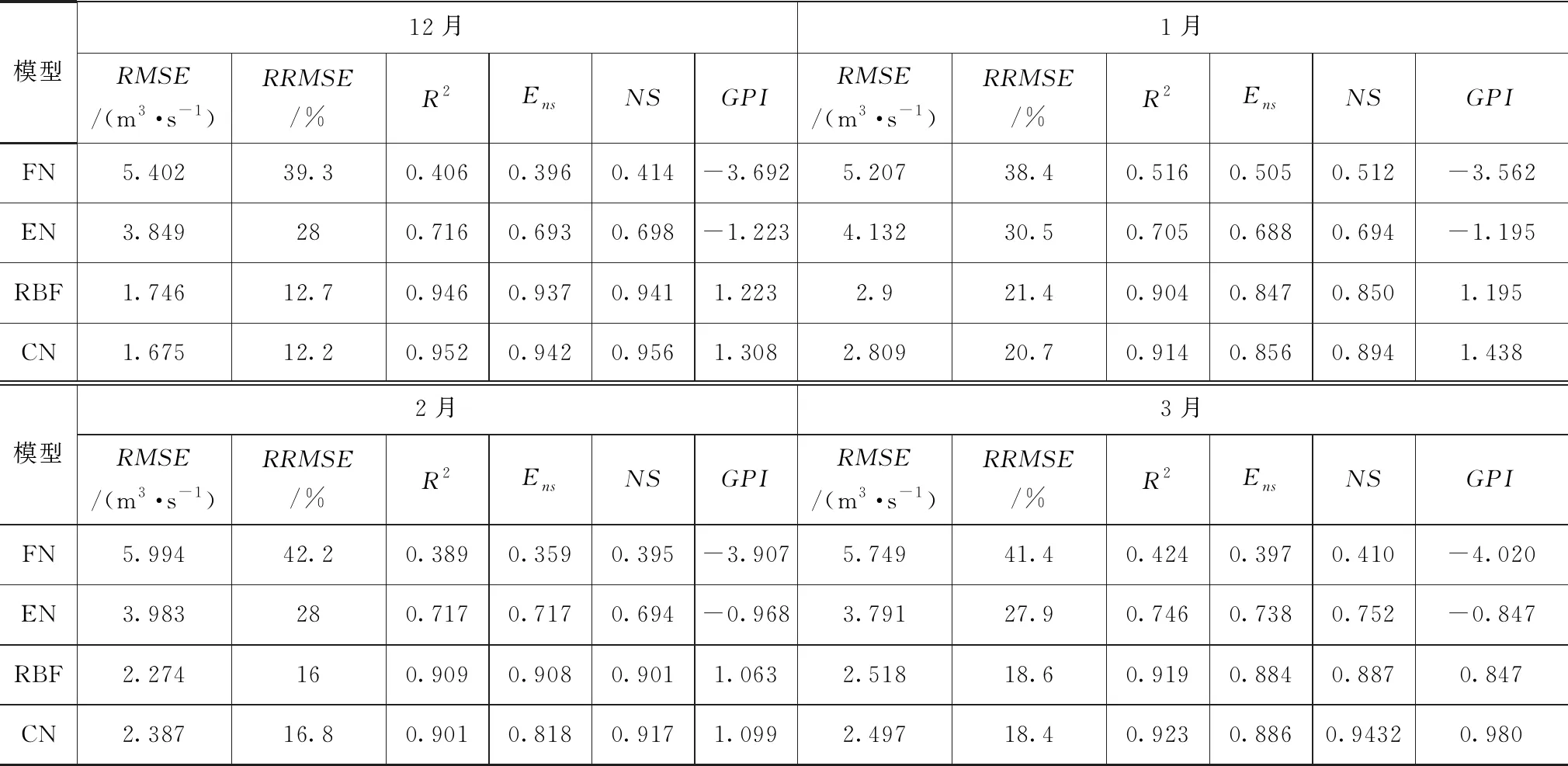
续表2
