基于大温差变幅的超大型弧形闸门变形规律测试研究

张宗超，张 慧，任泽俭,李东明

(1.枣庄市鸿禹水利工程监理中心，山东 枣庄 277000；2. 南水北调东线山东干线有限责任公司，山东 济南 250109； 3. 水利部水工金属结构质量检验测试中心，河南 郑州 450044)

1 概述

水利部水工金属结构质量检验测试中心在国内外承担多项水利水电工程金属结构设备制造安装的监造和检测工作，受建设单位委托开展某水电站工程结构设备的制造和安装第三方检测工作，该水电站工程溢洪道表孔弧门属于超大型产品，宽9m，高18m，设计水头39m，外缘曲率半径33m，精度要求高，制造生产难度大。在工作中发现，弧门的制造尺寸在不同温度下检测结果有一定的差异，为了解变形规律，进一步指导工厂制作检验，决定采取高精度测量系统分时段、按周期监测其变形状况，目的是找出弧形闸门在大温差变幅下构件变形规律，为同类工程和其他工程提供借鉴参考。

2 制定测试方案

测试项目采取2种测量手段：变形量采用高精度全站仪测量系统和激光跟踪测量系统。温度采集采用红外热像仪，同时采集环境温度和对象温度。

全站仪测量系统选用徕卡TS50高精度全站仪，单机测量精度为测角0.5″，测距精度为0.6mm±1ppm/m，系统整体测量精度为R30m测量空间范围内优于0.5mm。采用后方交会测量原理。

激光跟踪仪测量系统选用徕卡AT402高精度跟踪仪，采用激光绝对测距原理，按照相位法进行ADM测距，相位法测距是测定仪器发出的连续正弦信号在被测距离上往返传播所产生的相位差，并根据相位差求得距离，相位法测距原理如图1所示。

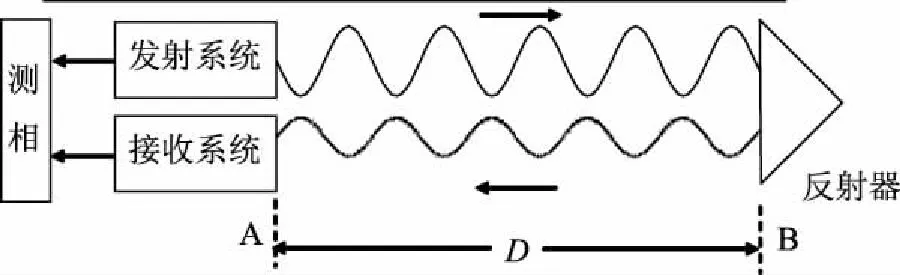
图1 相位法测距原理

采取2种测量系统是因为2者的精度等级不同，但都可满足弧形闸门制造质量尺寸检测的需要，运用2种手段可以加强比对，确保数据的严谨性。

3 温度及变形规律测试成果分析

测试项目选取了多个参数和对象，主要对弧形闸门曲率半径和面板(宽度方向)在不同时间、不同温度、不同位置进行测量。分别采集了不同时间段(3个完整的日历天)的气象温度和被测对象的温度，测量了3个完整的日历天的曲率半径和面板宽度的变形数据。表1给出了连续3d分时段采集的环境气象温度和对象(钢板)温度数据。

通过表1温度数据进行分析，第1天 15:00和第3天 10:30、13:30和15:10，环境温度较高，分别为32、32、34、32℃，被测对象温度最高时段均出现在13:00—17:30之间；在夜间和早上测量时，环境温度和对象温度数据差别不大；上午环境温度达到较高温度时对象温度并无较大变化，说明钢材未经历有效时长太阳照射，温度未深度积累。需要说明的是，被测对象14个部位均为实测提取，其温度变化反映的是太阳辐射阳面和阴面的不同。

通过比较2种测量系统分时段测试的温度数据(详见表2)及一个工作日内不同时段的面板宽度变化数据(详见表3)，分析以后发现：连续3d内环境温度的变化的最大差值为11.5℃，全站仪测量系统观测数据曲率半径的最大变化量为3.5mm，激光跟踪仪系统测得曲率半径的最大变化量为3.55mm，而1d内最高温度和最低温度下面板宽度的变化量为0.8mm。以上数据统计与分析均为郑州某工厂的测试数据。为了确保数据的充分性，测试组还到四川夹江某工厂制造现场在温差为10℃左右的2次温度工况下测得曲率半径的最大变化量为4.0mm，从2个地点，相同的温差，不同的时段验证了数据的一致性。

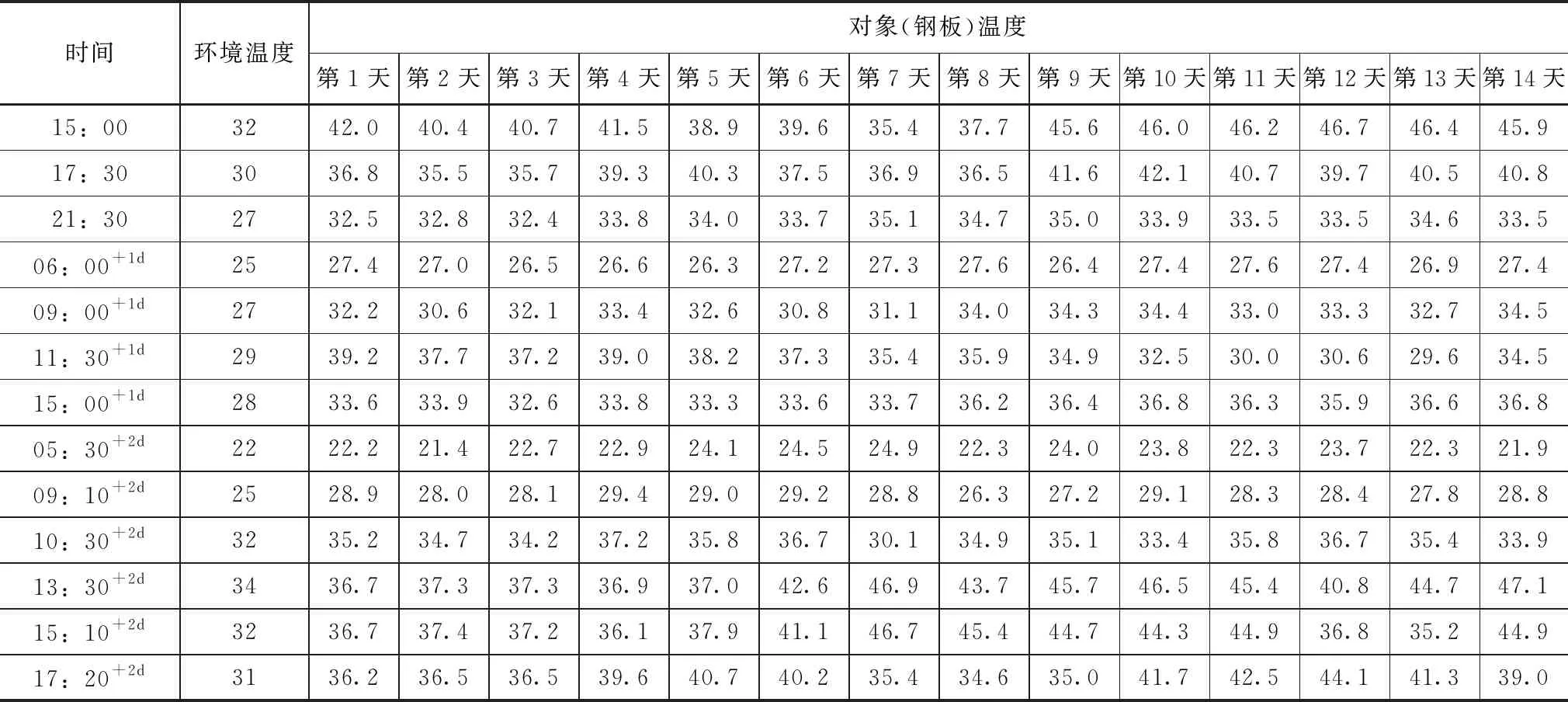
表1 不同时段环境及对象温度采集温度统计表 单位：℃

表2 不同时段弧门曲率半径测试统计表

表3 不同时段弧门面板宽度测试统计表

由图2—3可以得出结论，弧门曲率半径的变化与环境温度和对象温度均呈线性关系。

图2 曲率半径变形量和环境温度的关系

图3 曲率半径变形量和对象温度变化量的关系

4 结论

通过现场测试和数据统计分析，我们可以得出如下结论。

(1)弧形闸门面板宽度测试的环境温度变幅为11.5℃，对象温度变幅为22.2℃，宽度测试值最大变化量为0.8mm，面板在横向上未分节，说明面板宽度的变化量仅受温度因素影响。

(2)弧形闸门曲率半径测试的环境温度变幅、对象温度变幅与面板宽度测试条件相同，全站仪测量系统测得的最大半径变化量为3.5mm，激光跟踪仪测量系统的最大半径变化量为3.55mm，2种系统测得的变化量的量级一致。引起变化量的原因主要和温度有关，而且曲率半径变形量和温度呈现线性关系。

(3)对于大曲率半径的弧形闸门，在测得曲率半径偏差值处于允许偏差极限位置时，应考虑温度的影响。特别要考虑工地安装时的环境温度和闸门运行时的环境温度，尽量在接近上述环境温度时进行出厂检测。