超声速横向气流中液体射流的轨迹预测与连续液柱模型*

周曜智 李春 李晨阳 李清廉†

1) (国防科技大学空天科学学院, 长沙 410073)

2) (国防科技大学, 高超声速冲压发动机技术重点实验室, 长沙 410073)

对于液体射流沿壁面法向喷注进入超声速横向气流中的射流轨迹开展了理论与实验研究, 建立了连续液柱三维实体模型. 基于液体微元受力分析建立了连续液柱沿喷注方向横截面的截面变形控制方程, 计算了液体射流轨迹与横截面变形, 合理考虑了液体射流因发生表面破碎所引起的质量损失, 提出适用于超声速横向气流的连续液柱模型. 利用高时空分辨率的显微成像方法拍摄超声速横向气流中连续液柱的瞬时图像, 研究的参数变量包括液体喷注压降(1—2 MPa)、液体喷嘴直径(0.5 mm/1.0 mm)及液气动量比(3.32—7.27).研究结果表明, 采用连续液柱模型可以较好地预测中心面上的射流轨迹和三维空间上的液柱形态, 并可较为真实地反映实际流场特征, 预测结果与实验结果吻合良好.

1 引 言

在超燃冲压发动机的燃烧室中, 液体燃料经壁面法向喷注进入超声速的横流气体中, 在强烈的气动力作用下, 液体射流发生变形并向下游方向逐渐弯曲, 此间伴随发生一系列的雾化与混合过程. 在近液体喷嘴出口区域, 射流可以保持较为光滑的连续液柱形态, 但由于Rayleigh-Taylor 不稳定性[1]引起的表面波对射流迎风面的持续作用, 射流柱最终发生断裂, 此为液体射流的液柱破碎. 与此同时,大量细小的液滴由于强剪切力的作用从液柱两侧直接剥离[2], 在射流柱周围形成密集的液滴群, 此为液体射流的剪切破碎. 通过液柱破碎和剪切破碎, 大尺度的连续液柱结构破碎形成小尺度的液块和液滴.

射流轨迹和穿透深度是描述射流空间状态的两个概念. 前者通常是指自液体喷嘴出口处至液柱破碎位置的射流喷注路径, 而后者一般是指射流在不同流向位置穿透到横向气流中的最大穿透程度,也可理解为喷雾羽流的上边界[3], 在本文所关注的近液体喷嘴出口区域, 射流轨迹与穿透深度含义相同, 射流轨迹可认为是穿透深度的初始段. 由于穿透深度可以较好地表征出射流/喷雾在喷注方向上的空间分布特征[4], 研究者采用光学观测手段对超声速横向气流中液体射流穿透深度进行了实验研究并经过射流边界拟合得到了大量的经验公式[5−7],这些经验公式的表达形式一般分为幂函数、指数函数和对数函数三种形式. 实验结果表明, 液气动量比(q)、喷嘴下游沿流向的无量纲距离(x/d)、喷注角度(θ)和韦伯数(We)是影响液体射流穿透深度的主要因素[5,8−14]. 由于研究者们采用的光学成像原理、实验拍摄条件和图像处理手段不尽相同,这导致基于实验结果拟合得到的经验公式普适性较差, 无法将结论进行有效的推广. 吴里银等[15]采用脉冲激光背景光方法研究了多种工况条件下射流的瞬态边界振荡分布规律, 引入边界带的概念代替穿透深度并建立了射流振荡分布的经验模型, 成功预测了水射流在Ma= 2.1 横流中的振荡分布及穿透深度, 进一步提高了穿透深度经验公式的普适性.

在超声速横向气流中, 液柱断裂破碎的过程与亚声速横流中液柱断裂破碎的过程极为相似, 其在近喷嘴区域也存在特征较为明显的连续液柱结构[16].Mashayek 等[17]采用理论分析的方法对于亚声速横流中液体射流轨迹进行了研究, 综合考虑了因剪切破碎引起的液体微元质量损失与液柱横截面随时间的形变规律, 计算得到的射流轨迹与实验结果吻合较好. 李春[18]采用高速激光阴影方法研究了近喷嘴区域射流的精细结构与表面波特征, 阐明了表面波控制射流液柱破碎的机理, 提出了射流表面波振幅与波长的空间演化规律. 周曜智等[16]基于流体体积函数(volume of fluid, VOF)两相流模型并结合自适应网格在Fluent 软件中数值计算了水射流在Ma= 2.85 横流中的破碎过程, 研究了多种工况条件下连续液柱空间结构的变化规律. 研究表明: 自适应网格可以大幅缩减计算网格量并进一步提高两相流计算效率, 计算得到的射流轨迹与实验结果吻合较好. VOF 模型和CLSVOF(couple level set and volume of fluid)模型对于射流一次雾化过程的仿真存在较大优势[19−22], 但其计算结果极为依赖气液界面位置的网格分辨率, 而液体射流破碎过程是典型的跨尺度两相流问题(1 µm—1 mm), 喷雾下游的小尺度液滴往往由于网格分辨率不足被忽略计算. 为有效计算出下游小尺度液滴并对其雾化特性进行分析, Ashgriz 等[17]与Douglas等[23]采用实体-粒子耦合建模的方式, 将亚声速横流条件下一次破碎的连续液柱结构认为是物理实体, 并在连续液柱表面增添二次破碎初始液滴与二次破碎模型, 实现了喷雾全场的低成本计算, 其计算得到的下游液滴速度和液滴直径与实验结果吻合较好. 采用实体-粒子耦合建模的方式研究液体射流雾化破碎过程有三个明显的优点: 其一, 基于理论分析建立的连续液柱实体结构使得气流场的特征更为合理, 可定量预测液体射流轨迹; 其二,将连续液柱简化为物理实体, 有效地降低了用于捕捉射流一次破碎的计算网格量; 其三, 依照实验结果添加二次破碎初始液滴, 从而完成喷雾全场的精确数值计算, 实现下游液滴雾化特性的定量预测.由于实体-粒子耦合建模在预测亚声速横流中射流轨迹和下游液滴雾化特性等方面存在巨大优势, 因此, 本文尝试将其在超声速横流条件下进行合理推广, 以期达到预测超声速横流条件下液体射流轨迹、射流柱三维空间形态和下游液滴雾化特性的目的. 超声速横流下的液体射流一次破碎过程与亚声速横流下的液体射流一次破碎过程具有较多相似点. 其一, 由于壁面边界层的存在, 两者在近喷嘴区域都存在相似的连续液柱结构; 其二, 受气动加速影响, 两者在液柱迎风面均存在相似的表面波结构; 其三, 因气动剪切影响, 两者在液柱两侧均会发生剪切破碎. 与此同时, 两种横流条件下射流的一次破碎过程也存在一定差异. 超声速横流由于其具有更高的湍动能, 因此液体射流破碎过程往往也更加复杂. 比如, 由于液体射流对超声速横流的阻碍作用, 射流前方会形成一道特有的弓形激波, 这使得液柱迎风面上不同高度位置的气流速度存在较大差异, 而在亚声速横流中, 这一速度被认为是均匀一致的. 由于经过弓形激波后的横流速度仍然显著高于亚声速横流速度, 因此, 超声速横流下的射流柱变形、断裂和破碎过程发生更快, 液柱破碎位置更靠近喷嘴出口, 液柱破碎时间更短.

本文首先基于微元分析的方法研究了超声速横流条件下液体微元的受力情况, 建立了连续液柱沿喷注方向横截面形变方程, 考虑弓形激波的影响对横流气动力进行了合理修正, 提出了可同时预测液体射流轨迹与射流柱三维空间形态的CLC 连续液柱模型(continuous liquid column model). 最后基于PIV(particle image velocimetry)系统与显微镜头提出了一种高时空分辨率的显微成像方法, 拍摄得到了近喷嘴区域精细的连续液柱结构并对于CLC 模型计算结果进行了实验验证.

2 实验系统与数值仿真方法

2.1 超声速风洞与试验件

本文实验是在国防科技大学高超声速冲压发动机技术重点实验室二维下吹式超声速风洞[15]中进行的, 超声速喷管出口横截面为50 mm × 60 mm(H×W), 试验段长度为200 mm, 超声速风洞系统示意图如图1 所示. 风洞采用直连式设计, 工作过程如下: 上游高压空气在进入驻室段、稳定段后,紊流度大幅降低, 进入Laval 喷管后加速至设计马赫数进入试验段, 试验段出口与环境大气直接相连. 风洞采用高压储气罐提供高压的空气作为气源, 储气罐体积为20 m3, 空气气源压力大于10 MPa.风洞系统可通过调节驻室总压, 灵活调节试验段内超声速气流的静压、密度等流动参数. 论文研究中分别应用了马赫数Ma= 2.1 和Ma= 2.85的两种喷管, 两种马赫数下对应的气流参数如表1所列.

图1 超声速风洞系统示意图[18]Fig. 1. Schematic diagram of supersonic wind tunnel system[18].

表1 超声速横流参数Table 1. Supersonic cross flow parameters.

2.2 显微成像系统

为了验证CLC 模型预测射流轨迹的准确性,利用超声速风洞、双脉冲固体激光器、QM1 长距离工作镜头和CCD 相机搭建了超声速液体射流显微成像系统, 主要对比采用实验和理论计算两种方式得到的射流轨迹的差异, 成像系统原理图如图2 所示. 脉冲激光经过激光扩束器后, 通过散射板形成均匀分布的平面背景光源. 同时采用PIV 系统控制软件完成计算机、CCD 相机和同步控制器的同步控制; 激光器最大能量为500 mJ, 波长为532 nm,单脉冲宽度为7 ns, 能够提供足够的时间分辨率,保证“冻结”射流瞬态结构, 而不出现“拖影”现象[15],从而获得清晰的近场射流图像. 实验采用的CCD相机成像单元分辨率为 4000 × 2672.

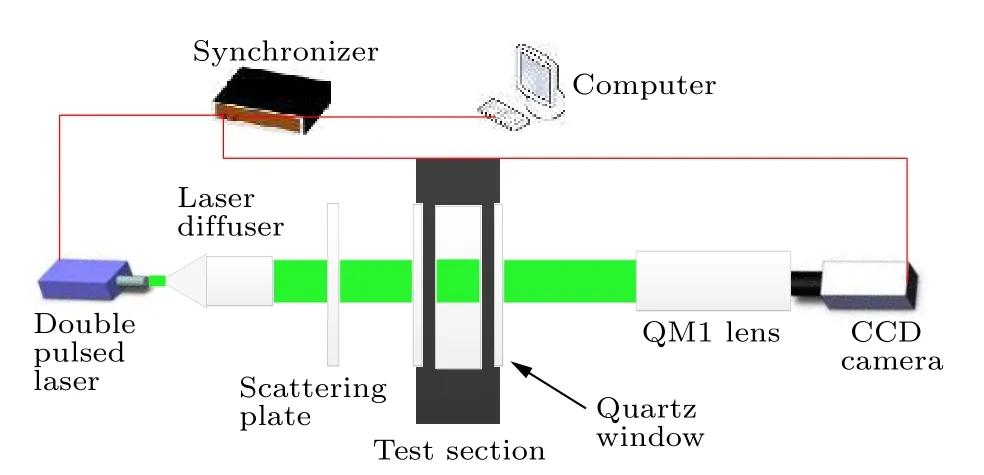
图2 显微成像系统原理图Fig. 2. Schematic diagram of microscopic imaging system.

图3(a)为实验中所使用的QM1 镜头, 其工作距离为0.55—1.52 m, 可实现对毫米级圆形视场的成像观测, 图3(b)为QM1 镜头工作特性曲线,QM1 镜头工作距离越小成像视场越小, 相应图像的空间分辨率则越高. 实验中 QM1 镜头的工作距离取为0.6 m, 显微成像实验获得的原始图像空间分辨率为1.57 µm/pixel.

2.3 气动阻力系数计算

采用数值仿真的方法计算连续液柱横截面的气动阻力系数, 计算中将连续液柱横截面气动阻力系数的计算简化为同等条件下二维液滴气动阻力系数的计算. 图4 为气动阻力系数计算域, 二维圆形液滴直径为1.0 mm. 由于液滴绕流流场存在对称性, 因此选取沿液滴水平中心线一半的流场区域作为计算域, 其中边界1 为横流入口, 设定压力入口边界条件, 总压为1.41 MPa; 边界2, 5 分别为壁面与液滴表面, 给定无滑移壁面边界条件; 边界3为横流出口, 设定压力出口边界条件; 边界4 为对称面, 给定对称边界条件. 采用基于密度基的求解器进行计算, 湍流模型选择k-ωSST 模型, 控制方程采用二阶迎风格式求解. 采用三种不同分辨率的网 格 对Ma= 2.85,总 压 为1.41 MPa,总 温 为300 K 横向气流中直径为1.0 mm 的圆形二维液滴的流场进行数值计算, 对液滴附近的网格进行了局部加密(图5). 表2 为采用三种网格计算得到气动阻力系数. 由表2 中数据可知, 中等网格和密网格计算得到的阻力系数基本相同. 图6 与图7 分别给出了对称面上流向速度分布及二维液滴表面的压力分布, 中等网格与密网格的分布曲线基本吻合. 综合考虑数值计算的精度需求和计算效率, 选择中等网格进行液滴阻力系数的计算. 针对不同椭圆率e(e=b/a)的二维液滴进行计算时, 保持网格数量与中等网格数量相同, 液滴表面的最小网格尺寸为 0.01d.

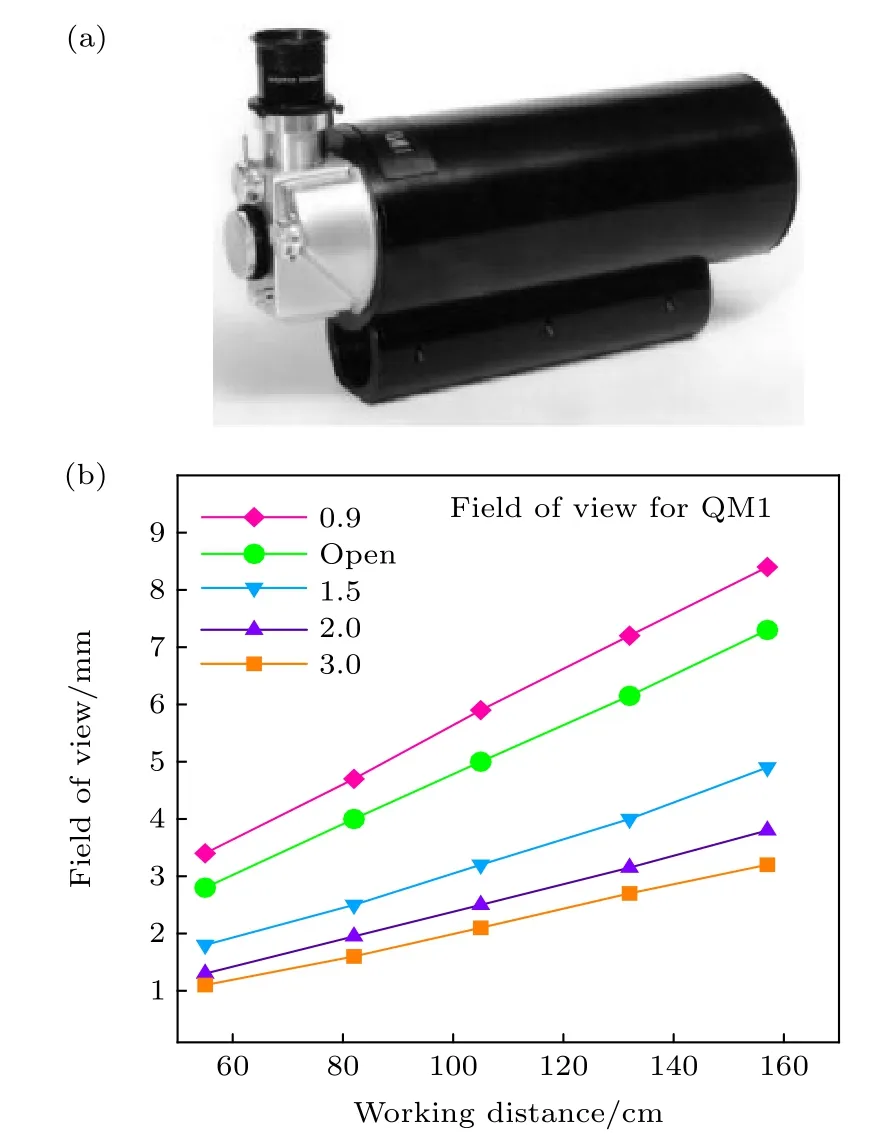
图3 显微成像系统原理图 (a) QM1 镜头; (b) QM1 镜头工作特性曲线Fig. 3. Schematic diagram of microscopic imaging system :(a) QM1 camera lens ; (b) QM1 microscopy camera lens working characteristic curve.

图4 液体微元的受力分析示意图Fig. 4. Aerodynamic drag coefficient calculation domain.

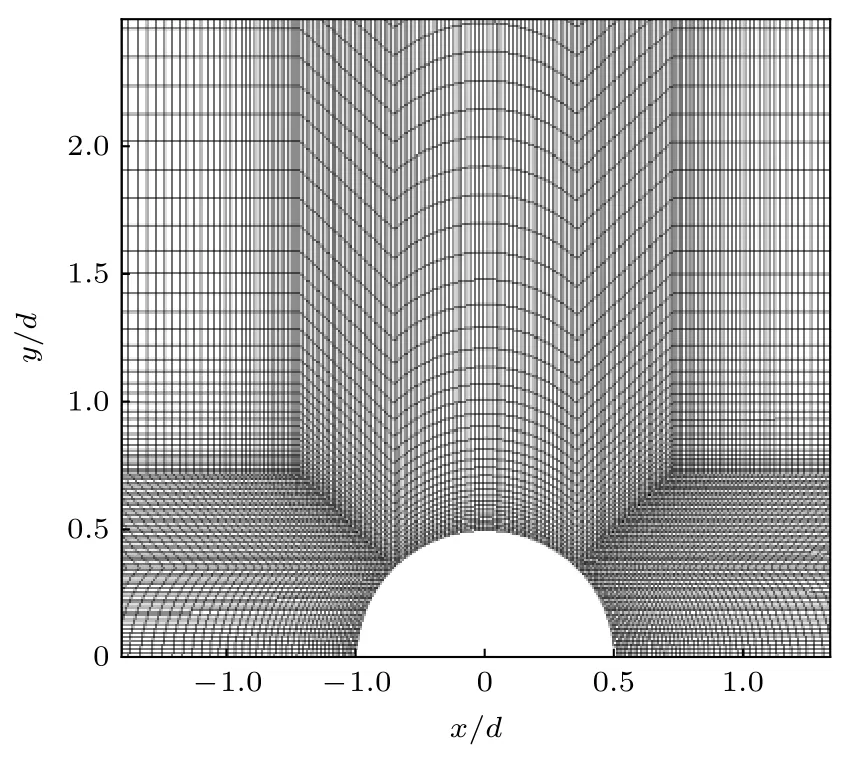
图5 二维液滴附近网格Fig. 5. Grids near the 2D droplet.

表2 不同网格计算得到的气动阻力系数Table 2. Aerodynamic drag coefficients calculated from different grids.

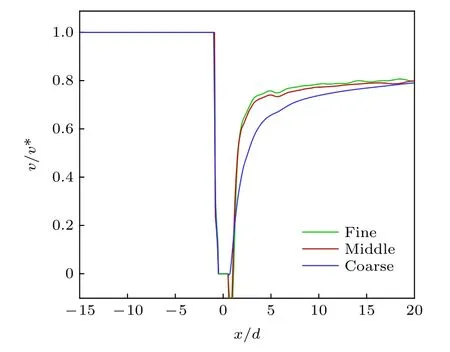
图6 对称面流向速度分布Fig. 6. Symmetrical flow velocity distributions.

图7 二维液滴表面静压分布Fig. 7. Surface static pressure distributions of 2D droplet.

3 连续液柱建模

图8 为超声速横向气流中连续液柱变形分区示意图, 主要分为光滑液柱区域、弯曲液柱区域与稠密液块区域. 本文研究的连续液柱是指液体喷嘴出口到液柱断裂之间的连续液体部分, 它包含了光滑液柱区域与弯曲液柱区域. 在超声速横流的持续作用下, 液体射流柱迎风面出现表面波并伴随出现液滴剥离的现象, 表面波不断发展使得射流柱断裂并形成大尺度的液块, 这一过程为液体射流一次破碎过程. 其中, 射流柱断裂过程是一次破碎过程中最为重要的特征. 由于亚声速横流情况下表面波的发展较慢, 射流柱表面一般较为光滑. 由于壁面边界层的存在, 近喷嘴区域气流速度较低, 液体射流依然存在特征明显的连续液柱结构, 但由于横流气动力较强, 射流柱同时在多个方向上发生剧烈的结构变形, 并伴随部分液滴从射流柱两侧直接剥离的现象, 这使得射流柱附近的气相流场变得极为混乱, 研究难度较大.

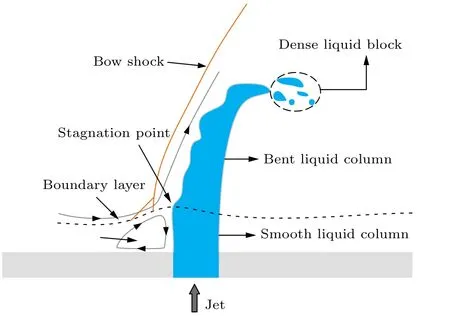
图8 连续液柱变形分区示意图Fig. 8. Schematic diagram of continuous liquid column deformation partition.

为研究射流柱附近复杂的气相流场, Li 等[24]对实验结果和数值计算结果进行了时间平均处理,并从中总结了气相流场中存在的普遍规律, 由此发现并证实了射流下游反转漩涡对的存在. 本文同样采用基于时间平均的方法, 提出直接建立具有表征时均特征的连续液柱(实体), 从而实现实体-粒子耦合建模. 若要实现超声速横流条件下实体-粒子耦合的建模, 首先需要完成一次破碎“实体”的建立, 再通过“粒子”实现下游液滴雾化特性的预测.本文提出建立一种可较好表征气相流场时均特征的连续液柱实体模型, 该模型可用于计算一次破碎的“实体”, 模型建立前提出以下四点假设(如图9所示):

1) 忽略连续液柱表面的非定常特征, 着重考虑连续液柱的定常特征, 液柱表面光滑, 射流轨迹为光滑曲线;

2) 简化实际情况下射流柱在横向气流作用下的非轴对称空间变形过程, 认为射流横截面发生轴对称变形且横截面形状由圆连续的变为椭圆;

3) 射流横截面气动阻力系数的计算简化为二维椭圆液滴气动阻力系数的计算;

4) 将液柱前方的弓形激波简化为一道激波角已知的斜激波, 波后马赫数按照斜激波波后马赫数进行计算, 从而获取液柱迎风面上不同高度位置的气流速度.

连续液柱的空间结构可以近似认为是一段不断发生变形的三维“水管”, 连续液柱在中心截面的投影可以认为是这段“水管”的二维投影, 其迎风面的“管壁”表示的是中心截面上的射流上边界, 即射流轨迹; 其背风面的“管壁”表示的是中心截面上的射流下边界. 此外, 射流柱在喷注方向的投影可以近似认为是二维椭圆[25], 自液体流出喷嘴至射流一次破碎结束, 该方向上的投影形状由与喷嘴出口直径等大的圆形连续变形为椭圆形. 其中, 椭圆长轴为2a, 短轴为2b, 椭圆率为e(e=b/a). 随着液体的流出, 椭圆的长轴不断变长, 短轴不断变短(如图10 所示).

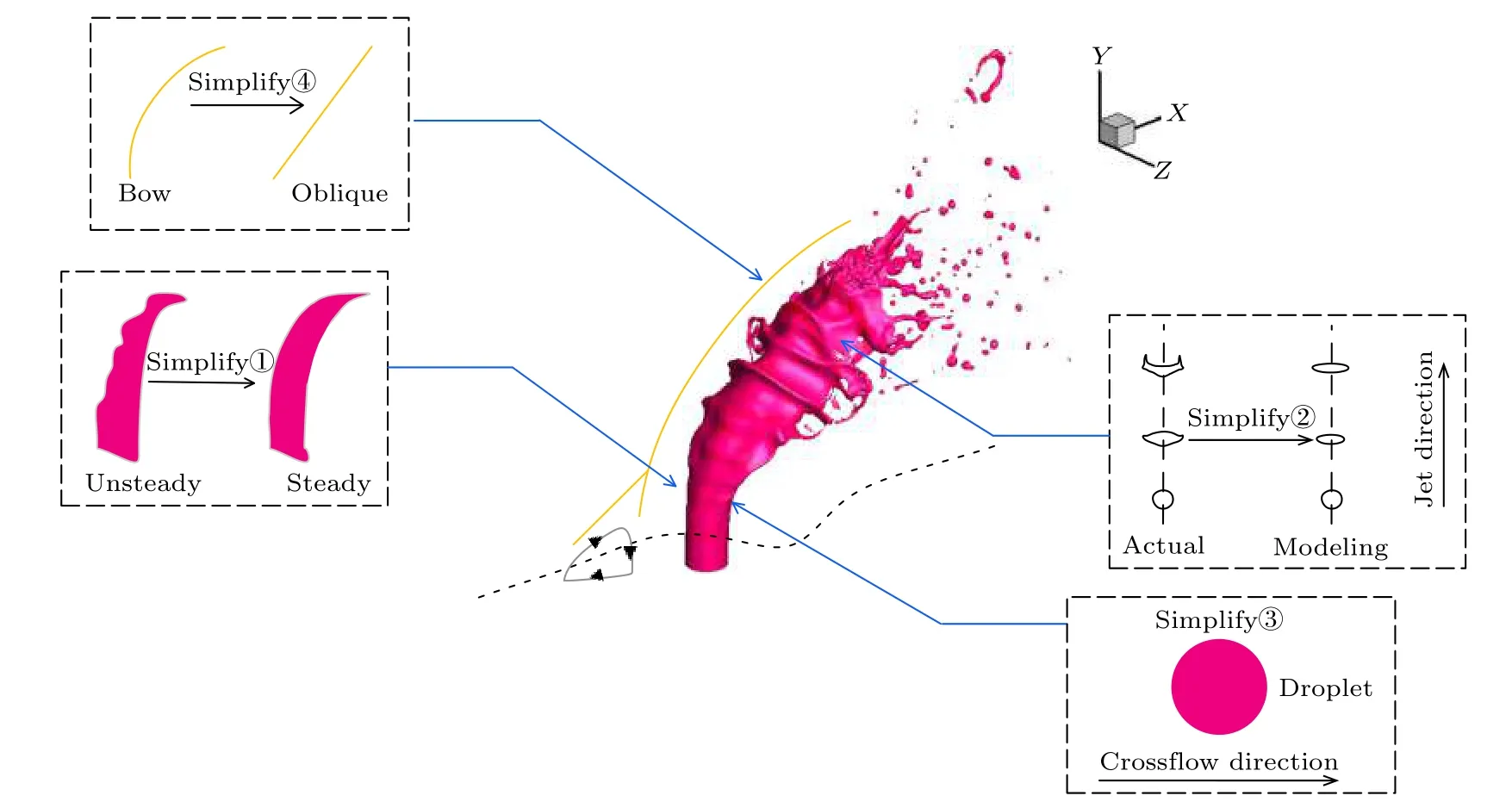
图9 模型假设示意图(粉色为液体射流一次破碎大涡模拟结果[19−22])Fig. 9. Schematic diagram of model hypothesis (The pink region is the result of large eddy simulation of liquid jet primary breakup[19−22]).

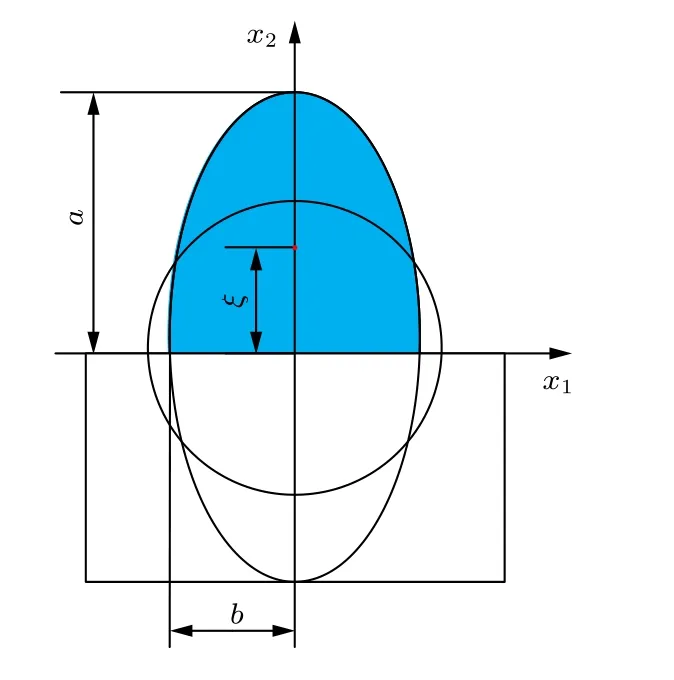
图10 液体微元横截面变形示意图Fig. 10. Schematic diagram of cross-section deformation of liquid microelements.

3.1 液体微元受力分析

液体射流喷入超声速横流后, 受气动力、表面张力和黏性力的共同作用发生雾化破碎. 为清晰地描述液体射流柱的受力情况, 提取液体射流柱中一段微元薄片进行受力分析, 其中微元薄片厚度为h.类比二维受力弹簧系统[26], 对受外界压力作用的二维液滴变形过程进行了受力分析, 二维液滴的变形主要受黏性力Fv、表面张力Fs和外界压力Fp的联合作用, 通过计算这三种力的线性项, 最终在x2方向上建立了力平衡方程:

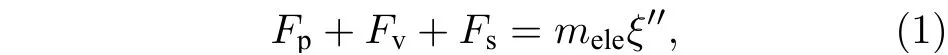
式中,mele为半液滴微元质量(0.5ρjπabh) ;ξ为半液滴微元质心到液滴微元中心的距离,ξ的初值为4r0/(3π) (圆形), 变形过程中为 4a/(3π) (椭圆形).

采用半液滴微元的质心运动来间接表示液体微元的运动, 并通过将每单位厚度液滴微元的能量耗散除以2ξ以获取黏性力, 黏性力的表达式为[17]

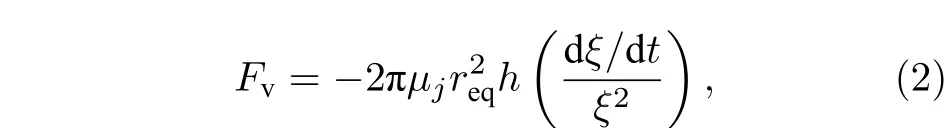
式中,µj为液体黏性;req为与瞬时椭圆横截面面积相等的等效圆的圆直径;req的值为(a+b)0.5, 由于椭圆横截面长轴长度与短轴长度的变化远大于req, 故认为req是常数.

半液滴微元表面张力的表达式[17]为

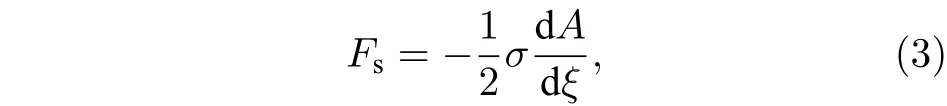
式中,σ为液体表面张力系数;A为液体微元侧面的表面积; 液体微元侧面的表面积为

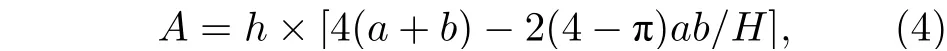
式中,H的表达式为

m的值取0.825, 将(4)式和(5)式代入(3)式, 得到半液体微元的表面张力的表达式[17]为

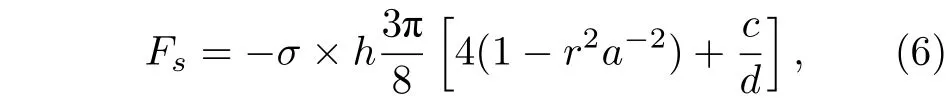
c和d均为常数:

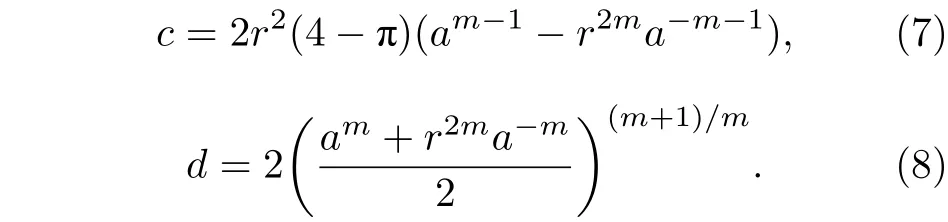
外部压力做的功[17]为

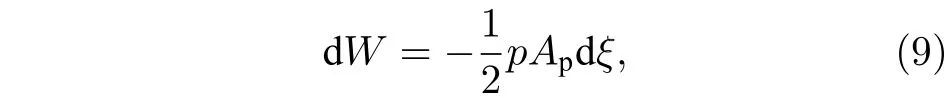
式中,Ap为压力作用面积(Ap=b×h);p为横流气体的总压

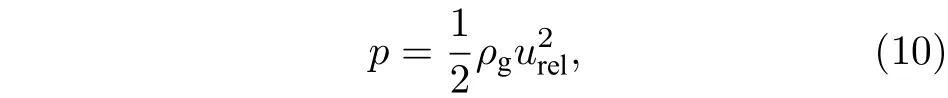
urel为横流气体相对于液体微元的相对速度,

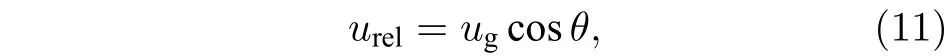
式中ug为射流柱前方实际横流速度, 下文对此速度进行了修正;θ为偏转角, 表示横流方向与液体微元的夹角.

将(10)式和(11)式代入(9)式, 外界压力的表达式为

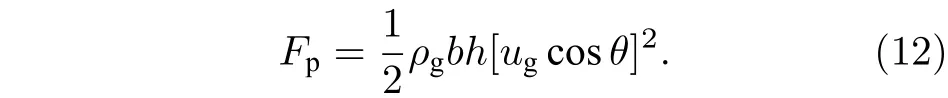
将(2)式、(6)式和(12)式代入(1)式后, 得到了液体射流柱横截面形变方程:

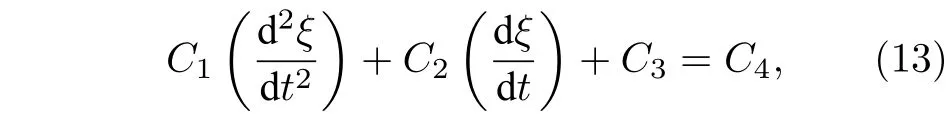
C1,C2,C3和C4的表达式为

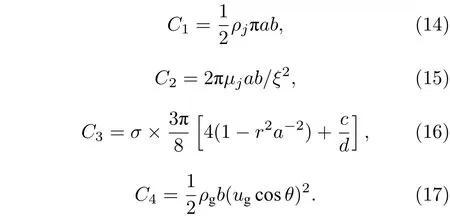
由牛顿第二定律, 液体微元受气动力和剪切力的联合作用(图11), 其中Faero为气动力,F1为液体微元与下方微元间的剪切力,F2为液体微元与上方微元间的剪切力.

液体微元所受气动力Faero为

式中,A=2a×h, 将(11)式代入(18)式, 得

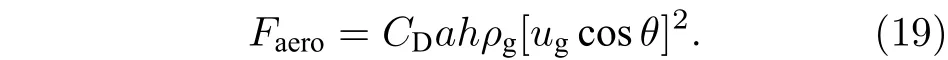
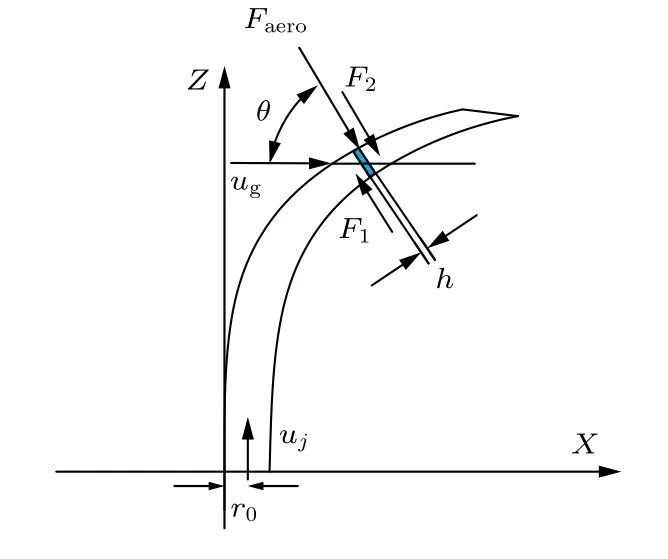
图11 液体微元的受力分析示意图Fig. 11. Schematic diagram of force analysis of liquid microelements.

Inamura[27]与Mashayek 等[17]对于液体微元的运动过程进行了分析, 液体射流沿射流轨迹方向速度保持恒定不变并且始终等于初始液体射流速度, 因此, 液体微元在x与y方向上的运动学方程:

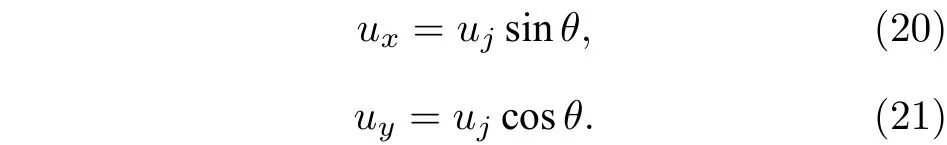
对于完整的液体微元, 由牛顿第二定律可知:

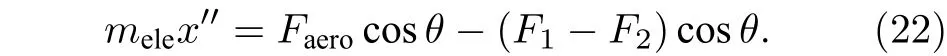
将(20)式对时间进行微分后代入(22)式后,获得了求解θ的一阶微分方程,

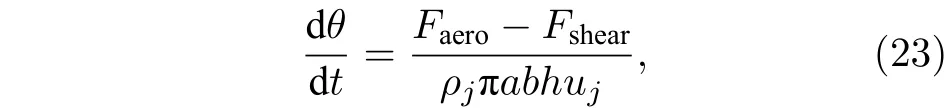
式中,Fshear表示的是上下相邻液体微元作用于所分析微元的剪切力合力, 其表达式如下:

式中,κ射流轨迹的当地曲率为

将(21)式对时间进行微分后代入(25)式, 当地曲率的表达式变为

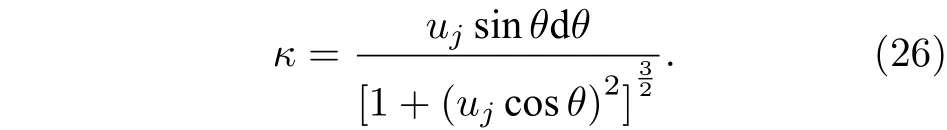
文中的射流轨迹是通过计算微元质心运动轨迹后间接获得的, 射流轨迹与微元质心运动轨迹的关系为

式中,Xcm,Zcm为液体微元质心运动轨迹对应的x方向坐标与z方向坐标.

3.2 液体微元气动力计算与修正

由3.1 节液体微元受力分析可知, 气动阻力系数CD和射流柱前方实际横流速度ug是影响液体射流柱横截面变形的两个重要因素. 对于气动阻力系数的计算一般分为两种: 一种是对于固定的破碎模式, 气动阻力系数也是一个定值[27−29], 计算时取一个经验常数即可; 另一种是忽略液体射流的三维效应, 将射流柱简化为二维液滴, 在CFD软件中计算不同椭圆率液滴的气动阻力系数, 之后通过线性插值的方式估计射流柱的气动阻力系数.Mashayek 等[17]采用这一方法计算了二维液滴的气动阻力系数, 并以此估计了射流柱的气动阻力系数.

图12 为无量纲速度云图, 超声速气流受液滴阻碍在液滴前形成弓形激波, 激波的脱体距离为0.425 mm, 这一距离与吴里银[30]实验得到1 mm射流弓形激波的脱体距离相近, 故本文采用的二维简化方法在一定程度上能够反映射流受到的气动阻力. 通过计算液滴附近的压力, 可得到多个椭圆率下液滴的气动阻力系数, 从而获得气动阻力系数随椭圆率的变化关系(图13).

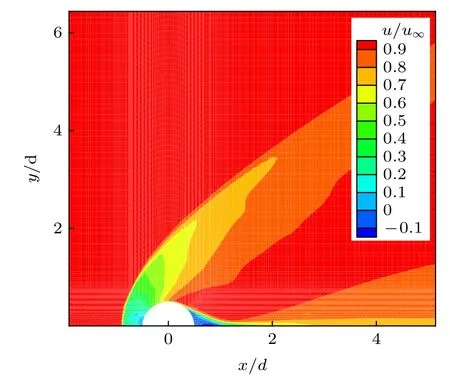
图12 二维液滴附近流向速度分布Fig. 12. Flow velocity distribution of 2D droplets.

图13 二维液滴气动阻力系数CDFig. 13. Aerodynamic drag coefficient of 2D droplet CD.

横向气流经过弓形激波后, 速度、方向均发生改变, 如果直接采用喷管出口的速度作为液柱前方的横流速度, 那么计算结果就会出现较大的偏差.图14(a)为李春[18]采用激光纹影拍摄得到的液体射流一次破碎结果. 从图14(a)中可以发现, 在超声速横流条件下, 液体射流前方存在一道明显的弓形激波. 横向气流经弓形激波后, 方向发生改变,速度明显降低. 如图14(c)所示, 本文将这道弓形激波简化为一道激波角已知的斜激波, 通过计算斜激波后的横流速度等效替代实际弓形激波后方的横流速度, 并基于此对气动力进行了修正. 如图15所示, 将斜激波前后的速度沿垂直与平行激波方向进行分解, 其中脚注“n”表示速度的垂直分量, 脚注“t”表示速度的平行分量.

横流转折角δ的计算公式为

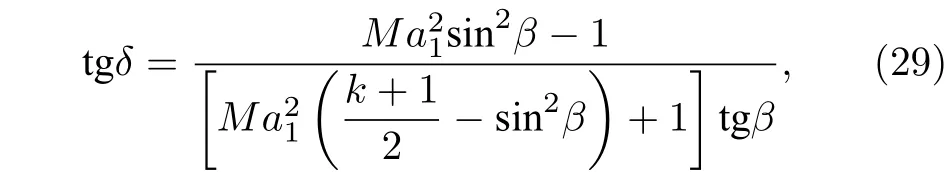
式中,Ma1表示斜激波前横流马赫数;β为激波角.

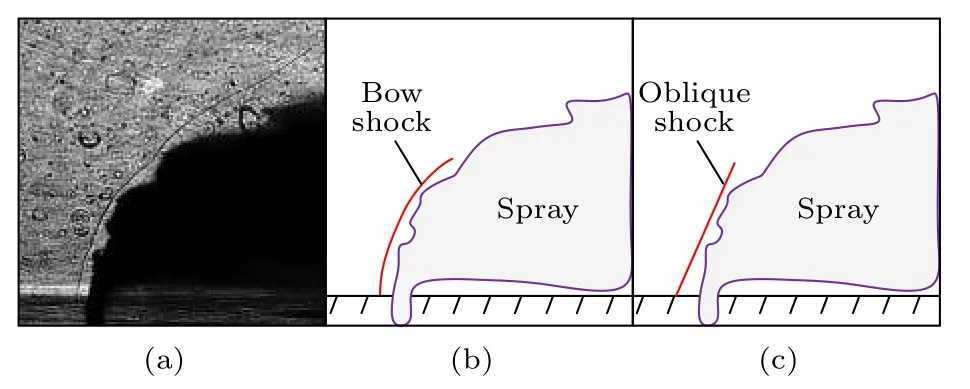
图14 斜激波简化示意图Fig. 14. Simplified schematic diagram of oblique shock.

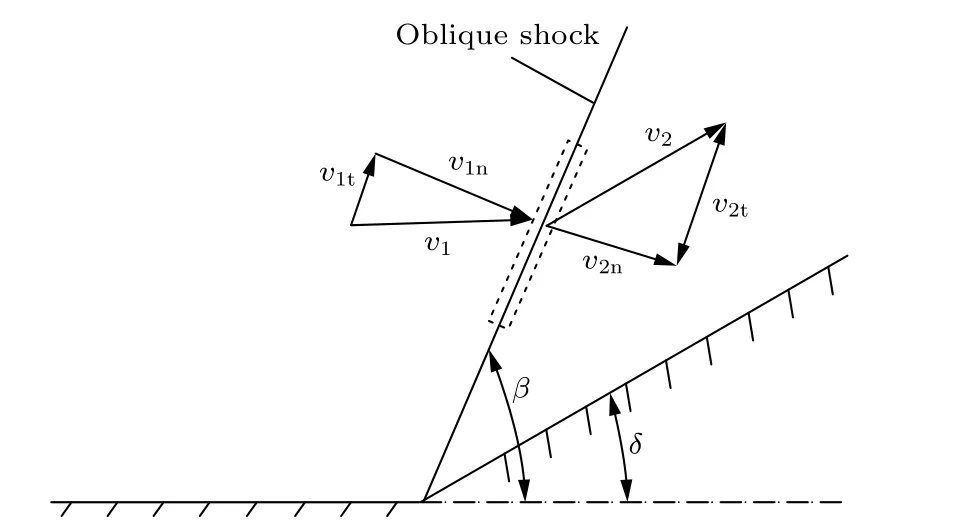
图15 斜激波波前/波后速度分解示意图Fig. 15. Schematic diagram of velocity decomposition of oblique shock wave front/back wave.

斜激波波后横流马赫数Ma2为

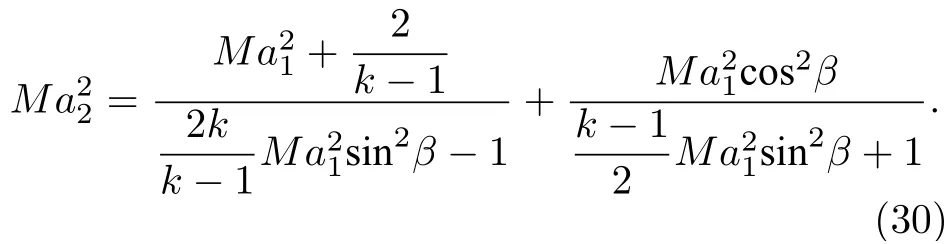
由波后横流马赫数Ma2可计算得到波后气流速度v2,将v2沿水平方向(平行于v1方向)进行分解即得到射流柱前方实际横流速度ug:

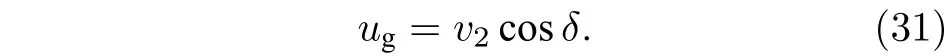
3.3 液体微元质量损失计算

剪切破碎对液体射流一次破碎过程影响较大,只有在特定的韦伯数范围, 液体射流才会发生剪切破碎[29]. 超声速横流一般具有较高的韦伯数, 在剪切力的作用下, 大量的液滴从连续液柱两侧直接剥离, 液柱两侧出现明显的“拉丝”现象[13]. Mazallon等[31]研究了多种工况条件下液体射流的剪切破碎过程, 并提出了临界韦伯数的概念, 当横流气体的当地韦伯数大于临界韦伯数, 液体射流便发生剪切破碎.

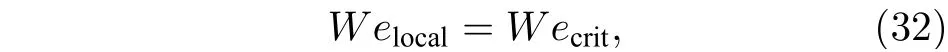
式中Welocal为当地韦伯数;Wecrit为临界韦伯数,本文Wecrit的值取为100.

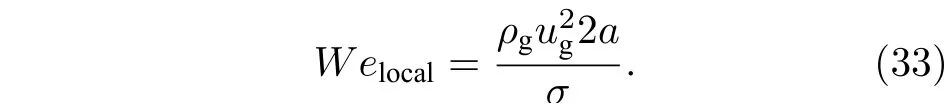
液体微元的质量损失[31]为

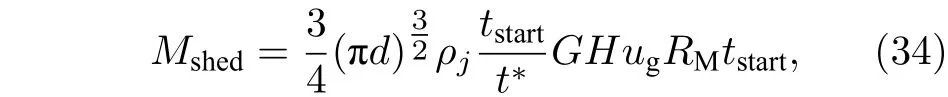
式中,tstart为从表面破碎开始所经过的时间;t∗为气动特征时间,

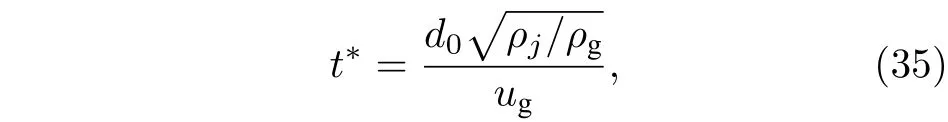
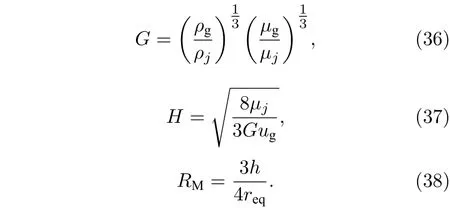
Ranger 和Nicholls[32]以 及Chryssaki 和 Nicholls[33]对于(34)式进行了两次修正. 第一次修正加入了ts/t∗用于控制液体剥离速率, 使剥离速率与离开剥离起点的距离基本呈线性关系; 第二次修正定义了质量比RM,RM为液体微元质量与质量损失的液体质量比值. 本文采用Chryssaki[33]修正后的质量比表达式, 通过液体微元质量间接获得了沿流向不同位置处剥离液滴的质量, 并将剥离液滴的质量计入横截面形变方程, 获得了更为准确的射流轨迹.

基于前文推导, 利用MATLAB 软件计算了液体射流轨迹和横截面变形. 采用四阶的龙格-库塔方法求解(13)式、(20)式、(21)式和(23)式, 时间步长为 1 0−6s. 其中, (13)式用于求解连续液柱横截面形状(a,b); (20)式和(21)式用于求解液微元质心运动轨迹; (23)式用于求解偏转角. 理论计算中横流气体和液体的工况参数见表3, 主要研究的参数包括: 马赫数Ma= 2.85/2.1, 喷注压降1 MPa/1.5 MPa/2 MPa, 喷嘴直径0.5 mm/1.0 mm, 其中Case 1(d= 0.5 mm)工况为本文基准工况.

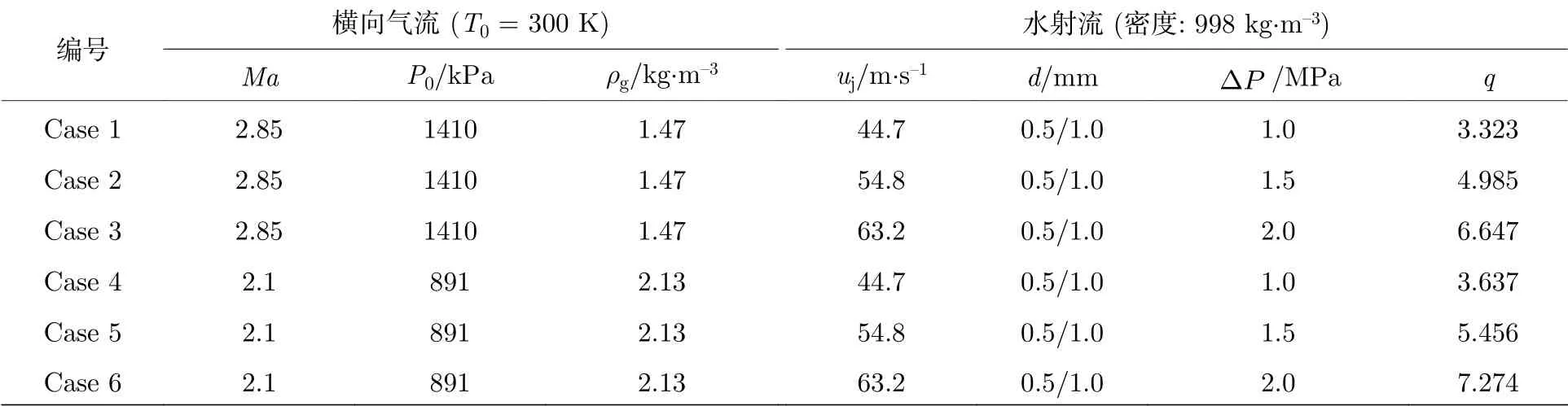
表3 理论计算参数Table 3. Theoretical calculation parameters.

3.4 射流横截面形变

图16 为不同喷嘴直径下射流横截面椭圆率的计算结果. 从图16 可以看出, 当横流马赫数与喷注压降保持不变时, 喷嘴直径越小, 射流横截面椭圆率变化越快. 这是由于喷嘴直径减小, 射流流量减小导致射流的惯性越小, 射流更易受横流气动力的影响, 故横截面的变形速度较快. 由于本文计算的横截面假设为椭圆, 半短轴的长度会在计算过程中不停地减小, 当减小到一定值(绝对值极小)时便已不符合实际液柱断裂的客观事实, 依照本文实验结果截取流向x/d= 2.0 位置作为基准工况下连续液柱横截面变形终点, 认为超过该位置处的射流开始发生液柱破碎, 同时, 定义液柱有效变形时间tvalid(tvalid=t/t*), 其中t为通过实验测量得到的液柱破碎时间,t*为气动特征时间, 通过计算, 本文工况均在tvalid= 0.7 附近发生液柱破碎, 由此认定tvalid= 0.7 为连续液柱结构计算的终点.

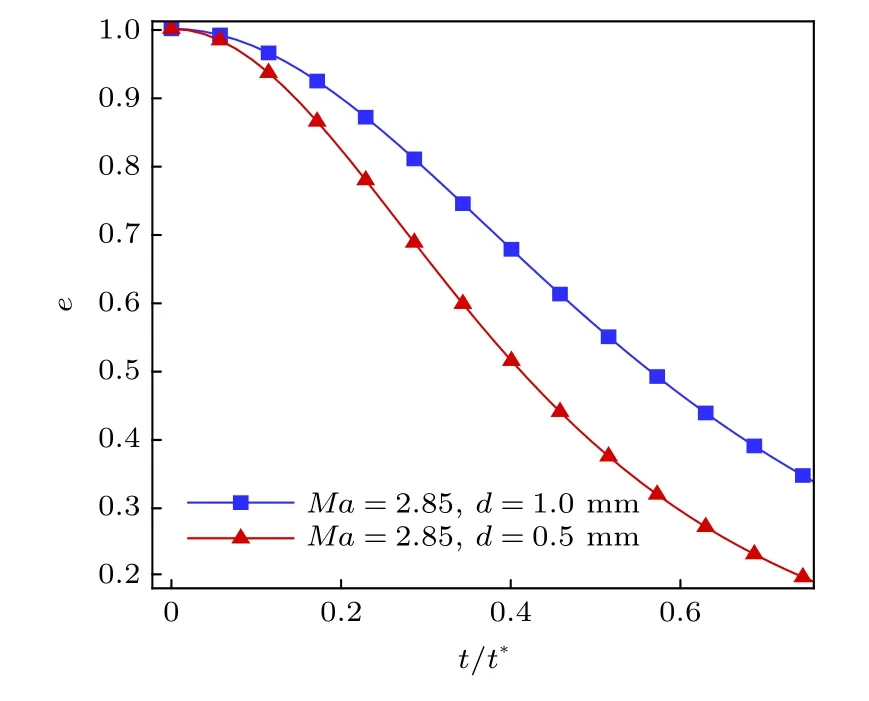
图16 液体微元横截面椭圆率计算结果Fig. 16. Calculation results of eccentricity of liquid microelement cross section.

图17 液体微元当地韦伯数计算结果Fig. 17. Schematic diagram of cross-section deformation of liquid microelements.

为了充分考虑剪切破碎对于连续液柱结构建模的影响, 图17 为液体微元附近当地韦伯数的变化情况. 由(31)式可知, 虽然横流气体在经过弓形激波后速度有了一定减小, 但其水平分速度仍然较大, 这导致当地韦伯数较高, 液体微元的原始质量因剪切破碎持续减小. 图18 为剥离液滴质量与液体微元原始质量的比值随液柱有效变形时间的变化情况. 从图18 可以看出, 横流马赫数越大, 液滴的剥离量和剥离速度就越大, 基准工况下, 液体微元的剥离质量占比在32%(质量流率为2.8 mg/s)左右.

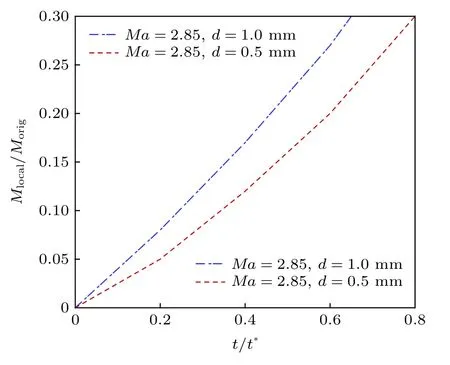
图18 剥离液滴质量计算结果Fig. 18. Schematic diagram of cross-section deformation of liquid microelements.

3.5 连续液柱模型

图19为采用CLC 模型对基准工况预测得到的连续液柱结构, 其三维空间上的分布范围列于表4. 从宏观上看, 计算得到的连续液柱实体较为符合研究者通过实验观测或数值仿真方式得到的射流柱形态; 此外, 计算得到的连续液柱在近喷嘴位置处基本保持完好的圆柱形态, 且随着流向距离的增加, 连续液柱沿喷注方向的横截面变得愈发狭窄, 这一点与李春[18]的实验结果吻合较好. 另一方面, 由于建模过程中忽略了射流柱迎风面的非定常特征, 计算得到的连续液柱的迎风面较为光滑, 这一点与实际破碎过程中连续液柱迎风面特征存在差异, 不过这一差异对气相流场的时均特性影响较小.

表4 三维连续液柱模型参数Table 4. 3D continuous liquid column model parameters.

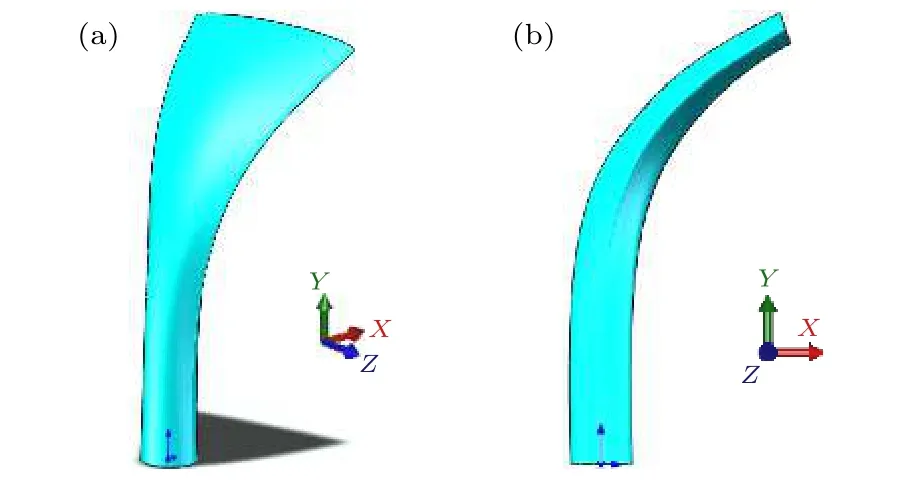
图19 CLC 模型预测得到的连续液柱结构 (a) 侧视图;(b) 正视图Fig. 19. Continuous liquid column structure predicted by CLC model: (a) Side view; (b) front view.

4 实验验证

本文采用MATLAB 软件中的图像边缘检测函数获取近场射流轨迹, 每个工况下提取60 幅瞬态图像的射流轨迹并进行叠加处理, 结果如图20所示. 从图20 中可以看到, 在喷嘴出口, 射流轨迹的脉动范围很小, 随着射流逐渐弯曲, 射流轨迹的脉动范围迅速增大. 此处定义表面波振幅: 取平均射流边界为基准, 以当地射流轨迹的法向方向取射流振荡宽度2As作为射流边界振荡的幅值, 表面波的振幅即为As. 为方便计算射流轨迹的法线向量,具体计算时取平均射流轨迹(图中红色曲线)作为样本, 采用最小二乘法拟合的边界线(图20 中蓝色曲线)作为基准计算当地的法向向量, 其中蓝色曲线与平均射流边界拟合的相关系数为0.99.

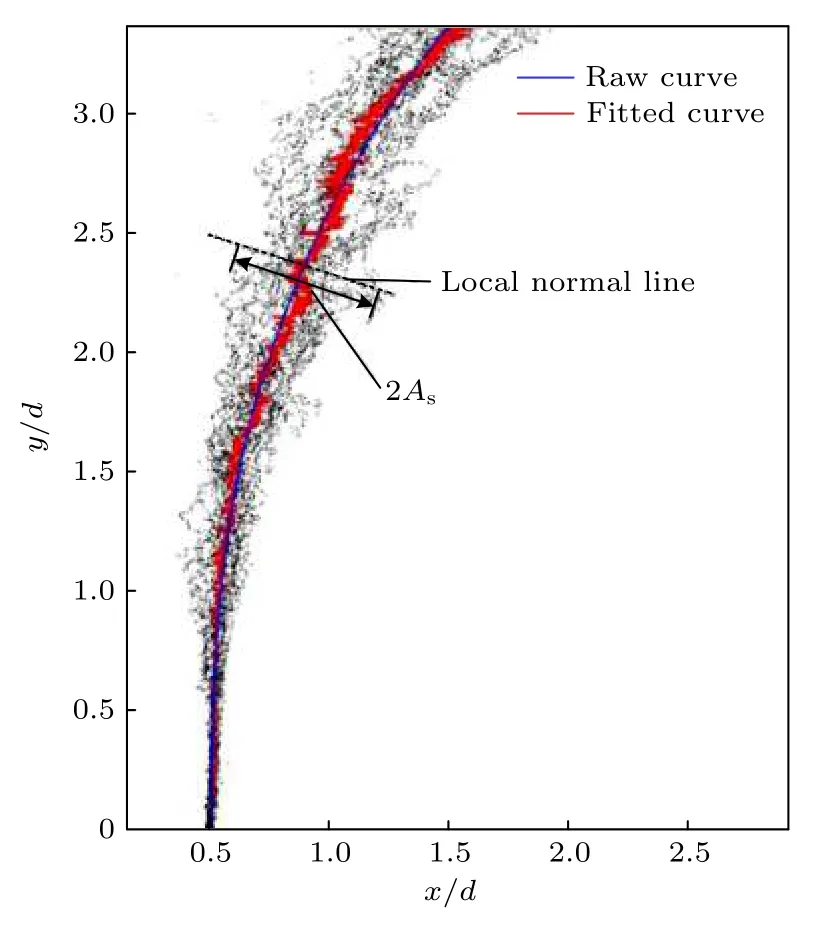
图20 射流轨迹叠加结果Fig. 20. Superposition result of jet trajectory.

图21(a)为超声速横向气流中液体射流柱的显微成像结果, 由于喷嘴出口附近的射流受到壁面边界层的影响, 气体横流的气动加速与气动剪切作用较小, 因此射流柱没有出现明显的弯曲变形, 表面波发展不明显, 液体表面较为光滑, 此处为光滑液柱区域, 即图中A 区域; 随着射流进一步穿透横流气体, 气动力的影响显著增强, 液柱的迎风面开始产生表面波结构, 液柱开始发生弯曲变形, 此处为弯曲液柱区域, 即图中B 区域; 随着表面波波长的持续增加(图21(b)), 液柱断裂成大尺度液块并进一步破碎成尺度更小的液块, 此处为稠密液块区域, 即图中C 区域. 具有高时空分辨的显微成像结果进一步表征了液体射流一次破碎中表面破碎(剪切破碎)、液柱破碎的发生过程与发生顺序, 表面破碎发生在弯曲液柱区域与稠密液块区域, 而液柱破碎发生在弯曲液柱区域结束位置. 图22 为不同压降条件下的液体射流近场瞬态显微图像. 对比三种不同的压降条件, 液体射流均存在特征明显的光滑液柱区域、弯曲液柱区域及稠密液块区域; 喷注压降的增大使得液体初始速度增大, 导致液气动量比增大, 喷嘴出口位置的射流轨迹更高, 连续液柱的弯曲程度更小. 同时, 随着喷注压降的增大, 射流迎风面扰动的特征尺度有所减小.

图23 比较了CLC 模型预测得到的液体射流轨迹结果与本文实验结果, 从图23 中可以看出,考虑质量损失后, CLC 模型预测得到射流轨迹结果与实验结果整体吻合较好, 射流轨迹变得更高,展向宽度也变得更小, 这是由于液滴从连续液柱两侧剥离后, 液柱在喷注方向上横截面面积变小, 截面变形速度变小, 射流迎风面面积变小, 液体微元所受气动力相应变小, 故射流可在喷注方向上喷注的更远; 由于本模型并未考虑射流迎风面变形、破碎情况, 因此, 沿流向各位置处液体微元质量的计算结果偏小, 这使得液体在喷注方向上的动量减小, 因此, 预测得到的射流轨迹较实验结果偏小.

在亚声速液体射流中, 液柱破碎位置一般距喷嘴出口较远. 图24 给出了研究者们[18,19]总结的亚声速液体射流液柱破碎的流向位置xb与本文实验结果. 本文实验研究工况下, 射流的破碎位置xb=1.0d—2.0d, 明显小于亚声速液体射流液柱破碎位置, 这是由于液体射流在超声速横流下受到的气动力更强, 射流液柱破碎位置更加靠近液体喷嘴出口, 同时由于两相流流场的非定常性, 相同横流韦伯数下, 液柱破碎位置会在一定范围内不断变化.图25(a)为不同喷注压降下射流轨迹的计算结果,图25(b)为不同喷嘴直径下射流轨迹的计算结果.随着喷注压降与喷嘴直径的增大, 近场射流轨迹弯曲程度减小, 射流穿透深度增强, 计算结果与实验结果吻合较好, CLC 模型可较好的反映近场射流轨迹的主要变化趋势和一般规律.

图21 喷嘴出口位置射流显微成像结果(基准工况)Fig. 21. Jet microscopic imaging results at the nozzle outlet (basic condition).

图22 不同喷注压降射流显微图像 (a) ∆ p = 0.97 MPa; (b) ∆ p = 1.49 MPa; (c) ∆ p = 2.05 MPaFig. 22. Microscopic images of jets with different injection pressure drops: (a) ∆ p = 0.97 MPa; (b) ∆ p = 1.49 MPa; (c) ∆ p =2.05 MPa.

图23 CLC模型预测得到的射流轨迹结果与实验结果(基准工况)Fig. 23. Jet trajectory results and experimental results predicted by the CLC model (basic condition).

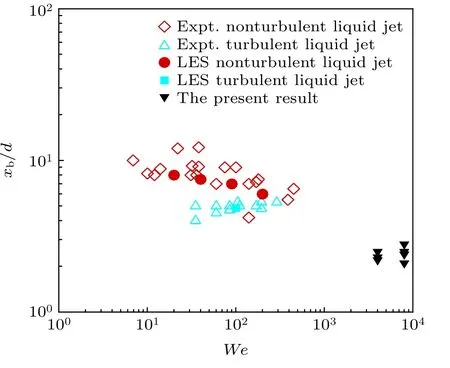
图24 超声速横流中液柱破碎位置与文献结果对比Fig. 24. Comparison of the broken position of liquid column in supersonic cross-flow with literature results.

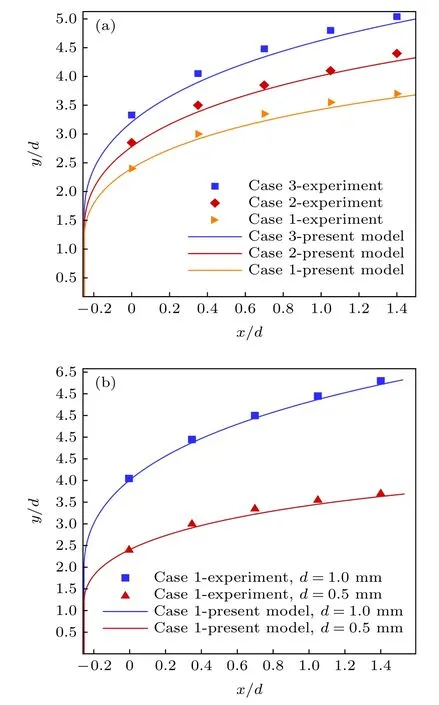
图25 不同动量比和不同喷嘴直径下射流轨迹计算结果与本文实验结果比较(a)d=0.5mm;(b)q=3.32Fig.25.Calcu lations for different mom entum ratios and diffent nozzle diam eters in com parison with experim ents: (a)d=0.5mm;(b)q=3.32.

5 结 论

本文研究了液体射流在超声速横流条件下的射流轨迹与连续液柱结构,基于液体微元受力分析推导出了连续液柱横截面形变方程与微元运动学方程,将二维液滴所受气动力等效为液体微元所受气动力,在考虑连续液柱前方弓形激波对流场的影响下,对气动力进行了修正,并通过质量比描述了连续液柱的质量损失,建立了可定量描述连续液柱时均形态的CLC模型,该模型可较好地预测液体射流轨迹和连续液柱的空间结构.在CLC 模型基础上,提出了一种基于PIV系统与显微镜头的高时空分辨率显微成像方法,拍摄得到了近喷嘴区域精细的连续液柱结构并验证了CLC 模型的准确性.