基于超导电路的奥特-汤恩斯分裂效应*

吴小宇 赵虎 李智†

1) (四川大学电子信息学院, 成都 610065)

2) (航空工业西安飞行自动控制研究所, 西安 710065)

基于约瑟夫森结的超导量子比特是一个宏观的人工原子, 通过微纳米加工的方法, 可以改变人工原子的基本参数. 三维Transmon 量子比特是目前已知退相干时间较长的一种量子比特, 该量子比特通过电容的方式与三维超导谐振腔进行耦合, 是一个人造的原子与腔场耦合系统, 可对原子物理、量子力学、量子光学、腔量子电动力学的各种效应进行实验验证. 本文制备并实现了3D Transmon 量子比特, 通过Jaynes-Cummings 方法寻找到了区分基态、第一激发态和第二激发态的最佳读出功率, 对共振条件下和非共振条件下的奥特-汤恩斯分裂效应进行了测试表征, 得到的测试结果与理论结果相符.

1 引 言

基于约瑟夫森结的超导量子比特是一个宏观的人造原子[1], 近年来一直作为量子信息的基本载体向着长退相干时间、低噪声、易加工、易拓展的方向不断发展[2,3]. 由于超导量子计算具备加工容易、耦合可控、基态容易制备、拓展性强等优点, 被认为是最容易实现量子计算机的方式, 吸引了IBM[4]、Google[5]等国际公司投入力量进行研究.超导量子比特由超导电路构成, 具有参数灵活可调的特点, 可与超导谐振腔相结合, 实现芯片级的腔量子电动力学(cQED)[6,7], 也可作为一个灵活的实验验证平台, 可对量子力学、量子光学、原子物理领域里的实验进行验证[8−10], 甚至部分自然原子不容易实现的实验, 也有可能在超导芯片上实现[11].除此之外, 传统的光场与原子的耦合较弱, 而超导电路与微波场的耦合, 可通过电容、电感等参数进行调节, 可实现原子与微波场的超强耦合, 也会产生一些奇异的量子光学效应[12−15]. 国内和国际上的研究小组基于三维 (3D) Transmon 量子比特与超导谐振腔的耦合, 演示了诸多相关的量子操纵方面的实验[16−18].

有部分研究小组对超导量子比特的奥特-汤恩斯分裂效应进行了研究, Baur 等[19]用色散读出法对Transmon 进行了奥特-汤恩斯分裂效应研究,相位量子比特的奥特-汤恩斯分裂效应通过隧穿原理进行读出[20]; 磁通量子比特与共面波导谐振腔耦合的系统中也观测到了奥特-汤恩斯分裂效应[21];Novikov 等[22]于2013 年在3D Transmon 量子比特中也观测到了奥特-汤恩斯分裂效应. 本文通过双角度蒸发的方法制备了Transmon 量子比特[23],并与铝基三维超导谐振腔[24]进行耦合, 构成了3D Transmon 量子比特[25]. 在10 mK 的超低温下,对3D Transmon 进行了基本的频域参数表征. 用Jaynes-Cummings[26]读出方法找到了区分量子比特处于基态|0〉,|0〉与|1〉的叠加态, 以及|0〉,|1〉和|2〉的叠加态的最佳读出功率. 该方法与Novikov等[23]所用方法不同的是, 仅需要给量子比特施加连续的微波激励信号, 而不需要对量子比特进行精准的时序测试, 从而降低了观测奥特-汤恩斯分裂效应的测试复杂度. 并研究了该量子系统在共振情况下和非共振情况下的奥特-汤恩斯分裂效应[20],实验与理论结果相符.

2 3D Transmon 量子比特

Transmon 量子比特是由电荷量子比特并联大电容, 并与谐振腔相结合的一种超导量子比特, 其等效电路如图1 所示. 由两个约瑟夫森结构成的电荷量子比特与谐振腔通过电容Cg耦合在一起.

图1 Transmon 量子比特等效电路图Fig. 1. Equivalent circuit diagram of Transmon qubit.

设电荷量子比特的栅电压为Vg, 栅电容为Cg,则栅电压吸引的库伯对数目为ng=CgVg/2e, 库珀盒的总充电能为4EC= (2e)2/2(CJ+Cg), 库珀盒的约瑟夫森能为EJ, 根据上述参数可写出电荷量子比特的哈密顿量H:

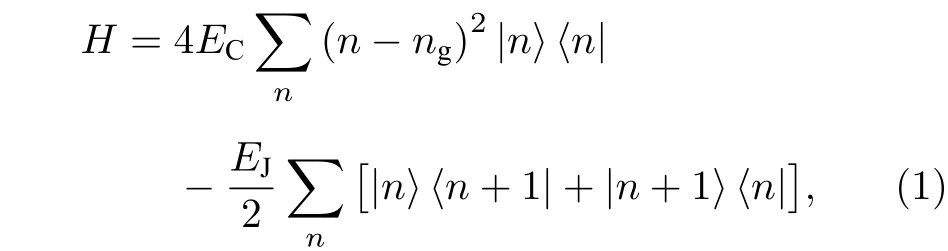
其中n为库珀对的数目,|n〉为粒子数算符. 构成电荷量子比特的约瑟夫森结较小, 其约瑟夫森能EJ远小于充电能EC, 该量子比特对电荷噪声极为敏感, 很小的电荷噪声将会使得偏置点ng发生较大变化, 给该量子比特并联大电容CB,使得EC减小,EJ/EC增大, 量子比特的能带变得更加扁平,即对于同样的电荷噪声, 只会引起较小的ng变化,量子比特的抗电荷噪声能力显著增强. 较早的Transmon 量子比特所用的谐振腔都是共面波导谐振腔[6]. Transmon 量子比特的哈密顿量由超导电荷量子比特推导得到, 本文所描述的Transmon 量子比特是由一个约瑟夫森结构成的.

2011 年, 耶鲁大学Paik 等[25]首次将Transmon量子比特与三维谐振腔耦合在一起, 构成了3D Transmon 量子比特, 经测试发现, 3D Transmon量子比特在退相干时间方面具有非常好的表现, 非常适合用做量子力学、量子光学、原子物理、腔量子电动力学等方面的验证平台.

制作3D Transmon 量子比特所用到的工艺主要为双角度蒸发工艺. 双角度蒸发工艺是制作约瑟夫森结的一种常用工艺, 其示意图如图2 所示. 双角度蒸发工艺需要形成具有悬空结构的电子束胶,即图2 中标注的W部分, 制作开始时, 首先从一个角度蒸发第一层铝, 厚度为30 nm, 蒸发速率为0.2 nm/s, 接下来要进行氧化, 氧化条件能够决定量子比特的能级分布, 氧化完成后, 进行第二个角度的蒸发, 第二个角度蒸发铝的厚度要略大于第一个角度的厚度, 为了能够保证边缘的连接, 第二层铝的厚度为50 nm. 图2 中的h和H分别为上下层电子束胶的厚度,W为悬空部分的宽度,X为约瑟夫森结的横向设计尺寸,M为电子束上层胶的开孔宽度,θ为电子束蒸发的角度.

图2 双角度蒸发工艺示意图Fig. 2. Schematic diagram of double angle evaporation process.

根据几何关系可以列出方程:

根据(2)式和(3)式, 在给定胶厚度h和H, 以及蒸发角度θ的情况下, 可以设计任意尺寸的约瑟夫森结. 但在设计时需要注意的是,θ一般不超过20°, 否则膜的均匀性就会受到影响.

本文制备的3D Transmon 量子比特实物照片如图3(a)所示, 图3(b)与图3(c)是样品的SEM 图片,经测试表征, 该3D Transmon 的基态|0〉到第一激发态|1〉的跃迁频率为f01=9.2709 GHz , 第一激发态|1〉到第二激发态|2〉的跃迁频率为f12=9.0120 GHz ,如图3(d)所示. 超导谐振腔的本征模态为fC=8.108 GHz , 有载品质因子为QL=4.8×105.

图3 3D Transmon 样品及能级分布Fig. 3. 3D transmon sample and energy level distribution.

3 Jaynes-Cummings 方法寻找最佳读出功率

对3D Transmon 量子比特的量子态读取常用的方法有色散读出法[6]以及Jaynes-Cummings 读出法. 色散读出法给超导谐振腔施加的读出信号功率较低, Jaynes-Cummings 方法基于三维超导谐振腔奇异的非线性效应, 可直接在谐振腔的本征模态fC处进行读出. 这种读出方法主要基于三维超导谐振腔对量子比特状态的“继承性”.

3D Transmon 的频域测试系统如图4 所示,总体的测试系统设计按照输入衰减、输出放大的原则进行, 这样能够提供最大的信噪比. 3D Transmon安装在10 mK 级. 微波源与网络分析仪的输出端口1 通过功分器进入稀释制冷机, 稀释制冷机在不同的温度区域安装了衰减器, 输入信号从室温环境进入到样品衰减了39 dB, 在输出端安装了两个隔离器用于隔离输出放大器的噪声对3D Transmon的影响, 在4 K 和室温下分别进行了两级放大.

用图4 所示的测试系统对3D Transmon 量子比特的频域特性进行了扫描, 得到图5 所示的结果.

注意图5 中的黄色部分, 当读出功率为–85 dBm时, 此时的谐振腔具有较大的传输系数, 当读出功率为–90 dBm 时, 谐振腔的传输系数有所降低, 当读出功率为–95 dBm 时, 谐振腔的传输系数几乎和噪底相同. 图5 中8.06 GHz 处传输曲线有一个较大的波谷, 这是由谐振腔的非线性效应造成的[26].

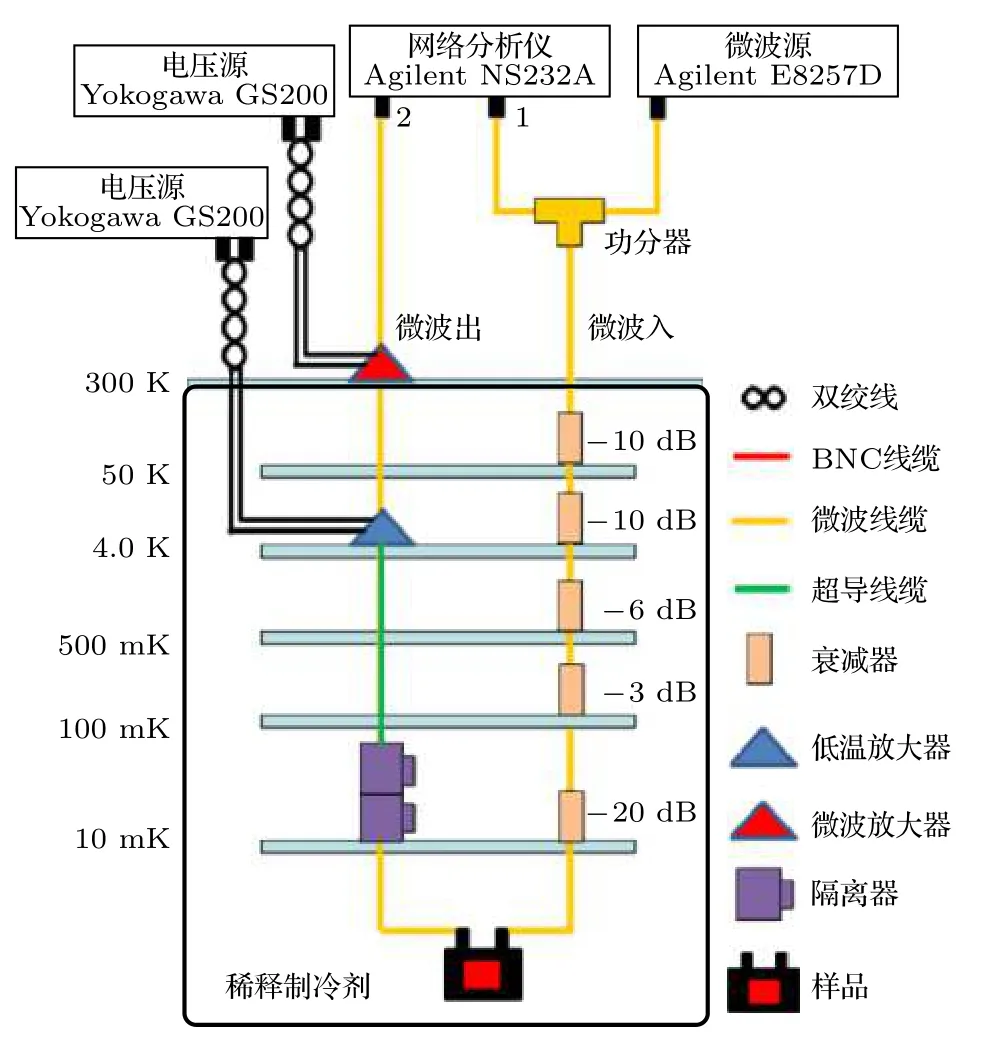
图4 3D Transmon 的频域测试系统Fig. 4. Frequency domain measurement system of 3D Transmon.

图5 网络分析仪变功率扫描S21 曲线Fig. 5. S21 curve of variable power scanning of network analyzer.

对3D Transmon 进 行Jaynes-Cummings 读出的测试系统在2014 年发表的论文[23]中进行了详细介绍. 给样品施加8.108 GHz 的微波脉冲信号, 并变化微波功率, 得到图5 中的黑色曲线, 该曲线反映出量子比特处于基态|0〉时, 读出信号随输入信号功率的变化情况. 给量子比特施加与f01=9.2709 GHz 相同的连续微波信号, 在8.108 GHz处进行读出功率扫描, 可得到图6(a)的红色曲线,此时由于连续的微波信号作用, 量子比特处于|0〉和|1〉的叠加态, 当给量子比特施加非共振频率的微波激励信号7.2709 GHz 时, 得到的曲线与没有任何微波激励信号的曲线完全相同. 对比三条曲线, 即可找出区分量子比特|0〉和|1〉状态的读出最佳功率点. 观测奥特-汤恩斯分裂效应, 涉及量子比特的三个能级, 因此需要寻找能够区分基态|0〉、第一激发态|1〉以及第二激发态|2〉的最佳读出功率点.对量子比特分别施加f01=9.2709 GHz 的激励信号,以及f01=9.2709 GHz 与f12=9.0120 GHz 的激励信号, 进行读出功率扫描, 得到如图6(b)所示的结果.

图6 (a)区分两个量子态的读出功率的优化; (b)区分三个能态的最佳读出功率优化Fig. 6. (a) Optimization of readout power for distinguishing two quantum states; (b) optimization for distinguishing three energy states.

当给样品施加f01=9.2709 GHz 连续微波激励信号时, 量子比特处于|0〉和|1〉的叠加态, 当给样品施 加f01=9.2709 GHz 与f12=9.0120 GHz 的 连 续微波激励信号时, 量子比特处于|0〉,|1〉和|2〉的叠加态. 图6(a)中黑色箭头标出的位置, 就是最佳的读出功率点, 在该功率下, 可以很好地区分量子比特的三个最低能态, 从而进行奥特-汤恩斯分裂效应的观测.

4 共振条件下的奥特-汤恩斯分裂效应

1955 年, Aulter 和Townes 利用OCS 分子做实验发现[27], 如图7 所示, 给该分子同时施加两束角频率分别为ωC和ωP的信号,ωC与量子比特|0〉|1〉的耦合拉比频率为ΩC,ωP与量子比特|1〉|2〉耦合的拉比频率为ΩP, 可以发现, 当ΩC逐渐增强时,|1〉到|2〉跃迁的单峰频谱将会劈裂为双峰结构, 也可称为缀饰态. 功率较强的耦合信号角频率ωC与原子能级差ωab的失谐可表示为δ=ωC-ωab. 由于他们最早发现了这个量子光学效应, 因此这种劈裂称为奥特-汤恩斯分裂效应, 或称为动态Stark splitting 效应.

图7 奥特-汤恩斯分裂效应示意图Fig. 7. Schematic diagram of ATS effect.

给3D Transmon 同时施加f01=9.2709 GHz 与f12=9.0120 GHz 的信号, 保持f01=9.2709 GHz 的信号较弱, 并在f12=9.0120 GHz 附近进行频率扫描, 逐渐增强f01=9.2709 GHz 信号的强度, 从而得到如图8(a)所示的奥特-汤恩斯分裂效应强度图.

图8(a)中黄线标出的三个功率点分别为耦合信号功率为–30, –20 和–10 dBm, 其二维图曲线如图8(c)—图8(e)所示, 可以明显看出, 当f01功率较低时, 扫描f12只能得到一个9.0120 GHz 的谐振峰, 但是随着f01功率的增加, 扫描f12可以得到两个关于9.0120 GHz 对称的谐振峰, 并且他们之间的距离随着功率增加而增加.

为了得到谐振峰的峰值与频率, 可通过洛伦兹曲线进行拟合, 双峰奥特-汤恩斯分裂效应曲线可通过两个洛伦兹曲线相加进行拟合. 图8(c)—图8(e)中的黑点为测试得到的原始数据, 红色曲线为洛伦兹拟合曲线, 用于拟合的公式为

图8 3D Transmon 量子比特的奥特-汤恩斯分裂效应 (a)奥特-汤恩斯分裂效应测试强度图; (b)奥特-汤恩斯分裂效应双峰间距与微波幅度的关系; (c)耦合信号功率为–30 dBm 时的奥特-汤恩斯分裂效应曲线; (d)耦合信号功率为–20 dBm 时的奥特-汤恩斯分裂效应曲线; (e)耦合信号功率为–10 dBm 时的奥特-汤恩斯分裂效应曲线.Fig. 8. ATS effect of 3D transmon qubit: (a) ATS test intensity diagram; (b) relationship between ATS peak spacing and microwave amplitude; (c) ATS curve at –30 dBm coupling signal power; (d) ATS curve at –20 dBm coupling signal power; (e) ATS curve at –10 dBm coupling signal power.

其中y0为曲线的偏移,A1与A2反映洛伦兹峰与横轴包围的面积,xc1与xc2是两个洛伦兹峰所在的位置,w1和w2表示两个洛伦兹峰的半高宽. 将不同功率下的xc1-xc2与耦合信号的微波幅度绘制在一起, 得到如图8(b)所示的散点, 将这些散点进行线性拟合, 得到图8(b)中的曲线, 可以看出拟合效果很好, 这与奥特-汤恩斯分裂效应理论符合得很好.

5 非共振条件下的奥特-汤恩斯分裂效应

只考虑小失谐情况下的奥特-汤恩斯分裂效应称之为共振情况下的奥特-汤恩斯分裂效应, 即耦合信号的失谐量δ远小于f01=9.2709 GHz 与f12=9.0120 GHz , 当耦合信号有较大失谐时, 对探测信号进行扫描, 得到奥特-汤恩斯分裂效应的双峰会随着耦合信号失谐的不同而产生偏移, 形成免交叉结构. 免交叉结构形成的两条曲线是(5)式哈密顿量的两个本征值.

对该哈密顿量进行本征值求解, 可以得到

在这种非共振情况下, 测量的时候扫描ωP, 双峰出现在ωP与缀饰态能级发生共振的时候, 此时测量得到的曲线应该满足方程:

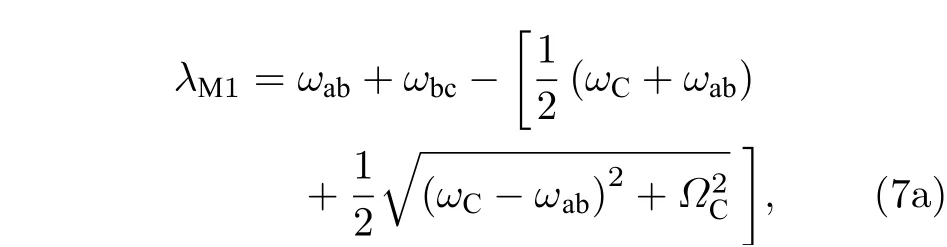
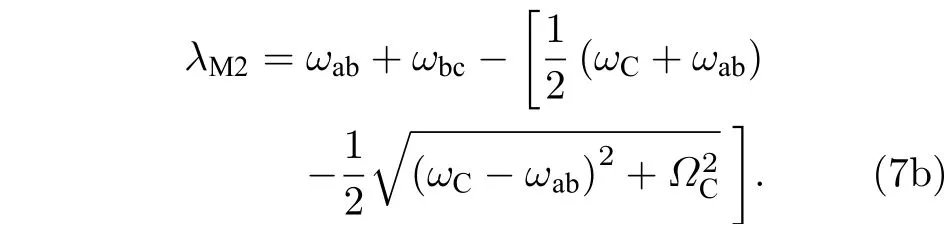
图9 非共振条件下的奥特-汤恩斯分裂效应免交叉测试强度图 (a) ω C的功率为–20 dBm; (b) ω C 的 功 率 为–15 dBm; (c) ω C 的功率为–10 dBmFig. 9. Anticrossing intensity test diagram of ATS under non resonance condition: (a) Power of ω C is –20 dBm;(b) power of ω C is –15 dBm; (c) power of ω C is –10 dBm.

图9 (a)—图9(c)为非共振情况下的奥特-汤恩斯分裂效应测试强度图和拟合曲线, 这三个强度图对应的ωC功率分别为–20, –15 与–10 dBm, 对应ωP的功率为–34 dBm. 图中黑色曲线是用(7a)式和(7b)式拟合的结果, 拟合时的参数为ωab/h=9.2713 GHz,ωbc/h=9.0125 GHz ,h为普朗克常数.

图9(a)—图9(c)对应的ΩC拟合值分别为4.6,8.5 以及16.6 MHz, 可以看出测试曲线与拟合曲线符合得非常好.

实际上, 免交叉能级结构的两个能级对应的本征态是|1,N〉和|2,N〉态的叠加, 有如下形式:

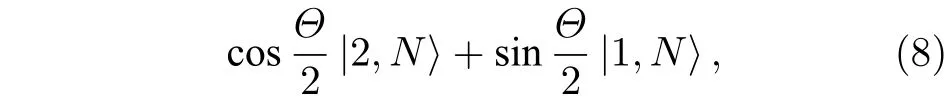
其 中,Θ=tan−1(ΩC/2δ)[23],当共振时,, 探测到两个态的概率幅相等, 反映在能谱上就是两条强度相等的谱线结构.

非共振时, 有两种情况, 首先在免交叉左侧,此时δ＞0 , 所以可以做如下变换:

从(9)式可以看出, 随着δ的增加, 探测到|2,N〉的概率将远大于|1,N〉的概率, 所以能谱上只能看到频率较高的|2,N〉态到|c,N〉态的跃迁谱线.

6 结 论

本文制作了3D Transmon 量子比特, 并对其基本参数进行了表征. 基于该量子比特最低的三个能级, 通过Jaynes-Cummings 读出方法选取能够最大程度区分最低三个能级的读出功率, 对共振情况与非共振情况下的奥特-汤恩斯分裂效应进行了测试, 实验结果与理论结果符合得较好. 3D Transmon量子比特是一个人工原子与超导谐振腔的耦合平台, 人工原子的参数可通过微纳米加工手段进行修改, 超导谐振腔的谐振频率也可以设计, 因此可作为量子力学、量子光学以及腔量子电动力学的实验验证平台, 对部分其他量子系统中不容易实现的理论实验进行验证.

感谢日本NEC基础创新实验室Tsai J S提供的样品加工支持.