基于加权马尔可夫链修正的ARIMA预测模型的研究
2020-12-14高鹤元刘如磊
郑 卓 曹 辉 高鹤元 刘如磊
(大连海事大学轮机工程学院 辽宁 大连 116026)
0 引 言
船舶主海水系统的正常运行,为船舶动力装置提供了充分的冷却条件,为船舶正常航行提供了保障。由于主海水系统直接连通舷外,工作环境恶劣,若能够根据海水系统中某些典型参数的变化进行有效分析预测,做到将事后维修转化为视情维修,对于使主海水冷却系统时刻处在一个正常运行状态以及延长设备使用寿命,具有重要意义。
目前,在工程上现有的方法主要分为两类:单一模型预测法和组合模型预测法。单一预测模型主要有:神经网络法[1],灰色预测法[2],回归预测法[3],时间序列法[4]。但是,单一模型在处理非线性、非平稳的时间序列上存在一定的不稳定性和局限性[5]。因此,目前组合模型预测法更为常见。徐梦茹等[6]在对地区降雨量的预测中提出马尔可夫与ARIMA组合模型,该模型虽然综合了两个模型的优点,但在模型组合时忽略了组合权重的确定对预测精度的影响。孙堂乐等[7]在对太阳黑子月均值预测中,提出将原始序列分解为若干子序列,对子序列分别建模预测并叠加重构。该方法由于会因为分解算法的固有缺陷,导致高频分量的非线性和非稳定性仍然较高。
本文提出一种采用加权马尔可夫链修正残差的ARIMA预测模型的组合模型。首先建立ARIMA模型对原始序列预测。ARIMA模型虽然能较好地反映序列的随机波动性,但会因为差分的过程导致信息丢失、精度降低的问题,因此,再结合加权马尔可夫链对预测残差进行修正。马尔可夫链适合描述随机波动性大的变量的预测问题,常被用于预测模型的残差修正过程中,在风力发电、降水量等预测中都取得了明显成效[8]。与单一ARIMA模型进行对比实验,结果表明本文提出的预测模型精度更高,实用性更强。
1 模型简介
1.1 ARIMA模型
ARIMA模型的主要思想就是将所得的时间序列视为一个随机序列,然后用一个数学模型来近似地描述它。ARIMA模型通过将非平稳时间序列经过d次差分转化为平稳的时间序列进行分析。
ARIMA(p,d,q)模型公式如下:
yt=θ0+φ1yt-1+φ2yt-2+…+φpyt-p+
εt-θ1εt-1-θ2εt-2-…-θqεt-q
(1)
式中:p为自回归模型阶数;q为滑动平均模型的阶数;d为差分次数;φi(i=1,2,…,p)、θj(j=1,2,…,q)为模型的待定系数;εt为t时刻的残差;yt为观测值。
1.2 加权马尔可夫链模型
加权马尔可夫链模型的主要思想是将一列相依的随机序列,经马氏检验后,用相关的各阶(各种步长)确定的加权马尔可夫链来预测未来值。
计算各阶自相关系数rk:
(2)

对各阶自相关系数规范化:
(3)
式中:wk为各步长的马尔可夫链的权重;m为按预测需要计算到的最大阶数。
结合式(2)、式(3)将同一状态的各预测概率加权和作为该状态的预测概率pi,即:
(4)
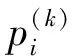
1.3 加权马尔可夫链修正的ARIMA模型
加权马尔可夫链修正的ARIMA预测模型的流程如图1所示。
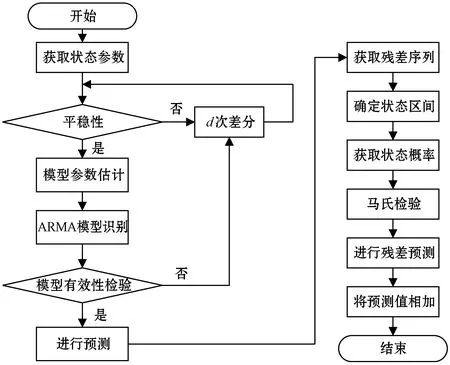
图1 加权马尔可夫链修正的ARIMA模型预测流程图
以ARIMA模型作为组合模型预测的第一部分,加权马尔可夫预测模型为第二部分。ARIMA作为对获取状态参数序列的预测,然后获取预测序列的已知序列部分的残差序列,用加权马尔可夫预测模型预测残差。最后用残差序列修正与其对应的参数序列,得到更为准确的预测值。
2 算例分析
2.1 问题描述与分析
如图2所示,在船舶海水系统中,大部分故障都会转移到中央冷却器的换热问题上,如海底门滤器脏堵、海水泵故障、海水管路有渗漏等会导致中央冷却器内的海水量不足,而不变量的低温淡水换热会使中央冷却器内的海水温度升高进而使船舶海水出口温度升高,若中央冷却器换热海水侧结垢,引起换热不足,会使船舶海水出口温度降低至正常温度以下。所以在监测船舶海水系统运行状态时,海水出口温度是一项重要监测指标。本文以预测“育鲲”轮海水出口温度为具体研究实例展开分析。

图2 “育鲲”轮海水系统图
2.2 数据获取
本文选取了“育鲲”轮在某航次航行时海水出口温度的数据。具体采集方式为每2小时获取一次参数数据,共采集了6天的数据即72组数据,取前5天即60组数据作为模型的输入,用于建立预测模型的基础数据,根据这60组数据进行建模并预测,后12组数据作为预测结果的验证数据[9]。如果进行长期的故障预测,随着时间的流逝,为了保证模型的准确性,可采取采集的数据顺次更迭的方式,使每次建模时数据总能保持72组数据。
2.3 ARIMA模型预测
(1)数据预处理。针对这6天的海水出口温度历史数据,取前5天历史数据作为建模的基本数据,并绘制中央冷却器海水出口温度T曲线图,如图3所示。

图3 中央冷却器海水出口温度图
可以看出,海水出口温度曲线呈由平稳到逐渐上升趋势。显然这组参数序列是不平稳的,所以应选用ARIMA模型进行建模,首先进行平稳化处理,即差分次数的确定。中央冷却器海水出口温度T经差分平稳化处理后如图4所示。

图4 中央冷却器海水出口温度1阶差分图
(2)模型识别。经过时间序列的平稳化处理和ADF检验之后,在MATLAB中使用autocorr和parcorr函数得出序列的自相关图和偏自相关图,如图5、图6所示。

图5 样本自相关函数图
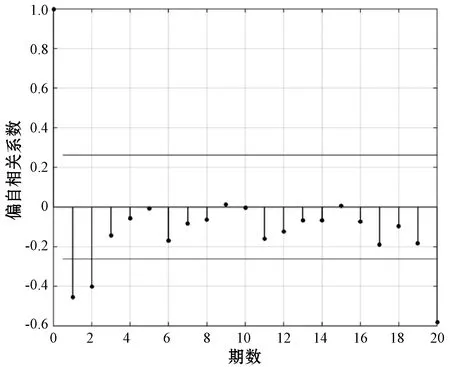
图6 样本偏自相关函数图
图5、图6显示自相关函数和偏自相关函数均拖尾,可以确定该模型应该为ARIMA(p,q)模型。在自相关图中,1阶和3阶的函数值可视为显著不为0,说明q可以取到3阶,同理在偏自相关图中,1阶和2阶的函数值显著不为0,说明p可以取到2。
由于仅依靠相关系数图判断模型的阶数具有一定的主观性,本文结合AIC(Akaike Information Criterion)、SC(Schwarz Criterion)信息准则进行了误差分析,选出最优模型ARIMA(2,1,3),如表1所示。

表1 模型检验结果
(3)模型预测。将最优模型在Eviews软件中采用最小二乘法进行拟合预测得到接下来的12期数据。
2.4 加权马尔可夫模型预测
(1)马氏检验。检验随机序列是否具有“马氏性”是应用马尔可夫链解决实际问题的重要条件,忽略“马氏性”的检验是不科学的,也是不严谨的。
计算残差序列Z的均值近似为0和均方差S近似为0.5。根据均值-均方差将序列划分为6个状态,如表2所示。
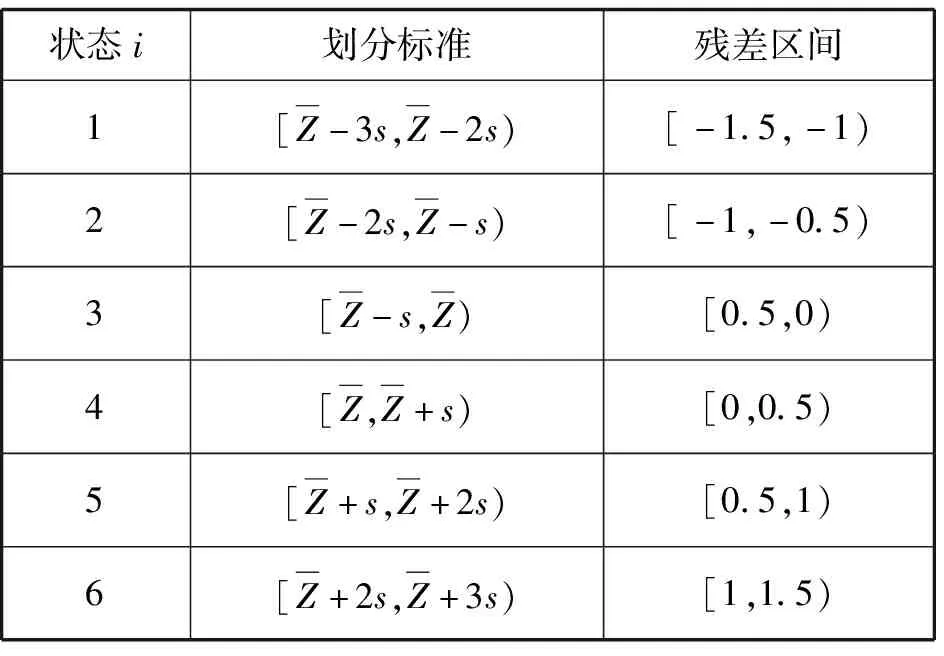
表2 残差状态等级划分
因此,可以得到残差序列中从状态i经过一步转移达到状态j的频数矩阵fij。
一步转移矩阵为:

表3 统计量计算表

(2)模型预测。在MATLAB中根据式(2)、式(3)可以计算出规范化后的各种步长的马尔可夫链权重,根据第1期到第60期样本序列的残差序列分别预测第61期到第72期残差序列,以预测第61期为例,如表4所示。

表4 第61期残差状态预测
可以看出,Pi=2.05对应的状态为4,由于预测的需求,需要将加权马尔可夫预测的状态值转化为具体数值,夏乐天[10]认为可以采用随机数学或模糊数学的方法予以推断,例如采用状态特征值结合线性插值法进行推断。
计算状态特征值公式为:
(5)

(6)
式中:
本例中,β取1.1,根据式(5)可以算出μ为4.728。用式(6)可得61期残差预测值:
同理剩下的11期残差值根据同样的方法预测,但是为了保证实验的准确性与时效性,每预测出新一期的数据就要替换掉一期的样本数据,从第1期开始。
2.5 加权马尔可夫模型修正ARIMA模型
因为ARIMA模型较为简单,只需内生变量而不需要其他外生变量,其实本质上只能预测线性关系,不能预测非线性关系[11],单一模型预测会存在误差,所以采用马尔可夫模型预测的残差修正ARIMA模型:
Tt=yt+x
(7)
根据式(7)可绘制修正后的预测值、ARIMA模型的预测值和真实值的曲线拟合如图7所示。

图7 拟合曲线图
可以看出,被修正的预测值每一期都比ARIMA模型预测值更接近真实值。为了更明显地看出修正模型较ARIMA模型预测的精度更高,本文分别计算了两个模型预测的平均相对误差,如表5所示。

表5 模型误差对比 %
可以看出,被修正模型的相对误差对比单一ARIMA模型相对误差大大降低,平均降低19%。随着预测期数的增加,加权马尔可夫对于模型修正的效果也逐渐降低,但是整体模型的预测精度还是达到了一个比较好的效果,所以在预测时并不是预测期数可以无限长,需要选取适当的预测期数,才能达到理想的效果。
3 结 语
本文分别采用加权马尔可夫残差修正的ARIMA模型与单一ARIMA对“育鲲”轮海水出口温度进行预测,结果显示加权马尔可夫链修正的ARIMA模型达到了更好的预测效果,对于12期的预测数据,在精度上有显著提升。该模型对海水出口温度预测精度的提高,为早日做到将事后维修转化为视情维修奠定了基础,同样也对船舶其他系统及设备故障预测方面提供很好的借鉴。
