锅炉配风系统优化
2020-12-13汤梅
汤梅
(马钢股份有限公司 安徽马鞍山 243000)
1 前言
钢铁企业所用燃煤锅炉具有复杂的结构和其惯性大,反应慢的动态特性,其参与的控制系统多存在滞后、非线性的特点[1-3]。
为了降低钢铁厂中锅炉运行投入与减少污染物的排放,开展燃煤锅炉燃烧过程的优化控制技术研究,对企业实现节能降耗,提高经济效益具有重要意义。目前钢铁厂对锅炉燃烧的调整大都是依赖传统的控制方式,一方面,传统控制技术在复杂系统的运用上仍存在许多不足,另一方面,由于检测装置的不精确性,使得风煤配比更难控制。如果仅凭借操作人员的经验来判断锅炉燃烧状况,很容易导致锅炉在不合理的配风情况下运行,造成燃烧火焰不稳定、局部未燃尽而结焦及风管堵塞煤粉等现象,机组的安全运行与燃烧经济性受到严重破坏[4]。因此,合理地调整风煤比来对锅炉燃烧工况进行优化,确保燃烧过程始终处于最佳配比燃烧状态,进而达到提高锅炉燃烧热效率和降低污染物排放的目的。
2 锅炉燃烧过程简介
锅炉燃烧的基本任务包括:不仅要提供足够的热量,能够快速满足外网负荷的需要,还要保证燃烧的经济性和锅炉稳定运行的安全性[5]。因此,燃烧系统应包括三个调节任务:跟踪负荷响应,调节最佳空燃比,保持炉膛负压不变。锅炉燃烧系统如图1所示。
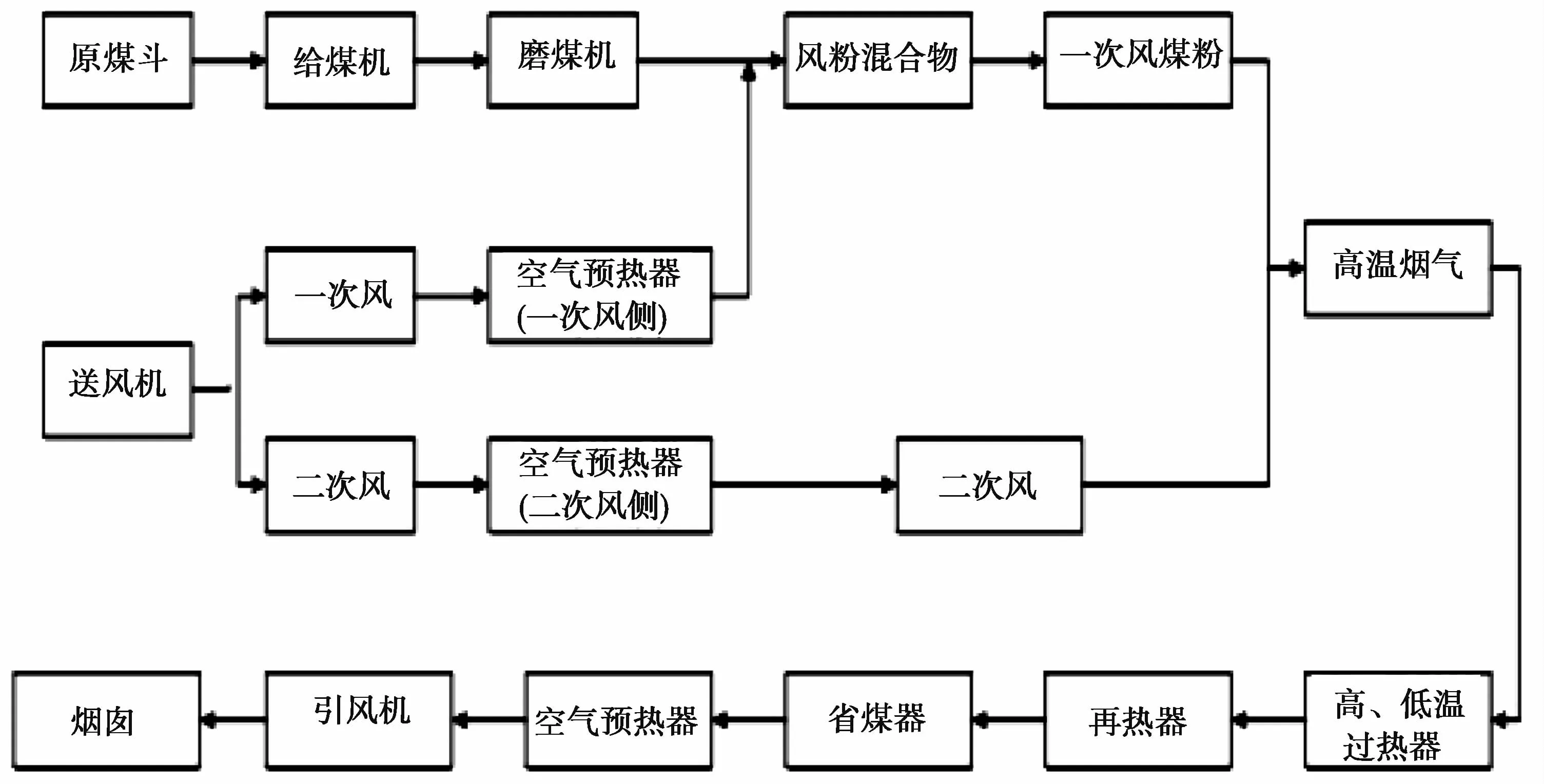
图1 锅炉燃烧系统图
在配风系统中,根据对燃烧过程的作用不同,进入炉膛的空气被分为一次风和二次风。其中,将煤粉送进燃烧器的空气称为一次风,主要作用是:防止煤粉堵塞管道并将其吹进炉膛以及提供着火初期所需的氧气。为了对锅炉进行合理配风,一次风首先要满足运送煤粉的要求,即不能使管道堵塞煤粉,然后是为煤粉燃烧提供氧气。当煤粉混合物被点燃时,进入炉内的空气称为二次空气。其主要功能是为煤粉的连续燃烧提供氧气。并对混合煤粉进行搅动使其均匀。混合煤粉和二次风在炉膛中继续燃烧,产生的烟气在引风机的作用下通过烟道,中途依次与过热器、再热器、空气预热器、除尘器等装置接触而发生热量交换,以提高锅炉燃烧热效率。
3 配风优化的数学建模
3.1 理论空气量计算
理论风量等于碳、氢、氧和硫元素的质量百分比与对应过剩空气系数的乘积。即

其中,Vth为理论空气量,不是特别说明的情况下,一般是指标准状态下的体积,以下符号的说明亦是如此;mC、mH、mO、mS分别为燃煤中元素C、H、O、S的质量百分比。由于化验室分析燃煤中还存在其他元素,那么氧元素和硫元素的含量的测量值就存在计算误差,故上述计算公式不能适用。这里采用的是利用煤粉低位热值[16]计算理论空气量的方法。

其中:Vth—理论空气量,m3/kg;
daf—低位发热量与理论空气体积的转换系数,m3/kJ;
Qd—低位发热量,kJ/kg。
根据当前的煤粉总流量,可以得到一共所需理论空气的体积为

其中:mfs—锅炉消耗的总煤粉流量,kg/h;
Vthc—燃烧所需的空气体积,m3/h。
以上计算公式均是基于标准实验条件下得到,实际需要的空气量往往大于理论值。实际中所需空气体积Vsj的计算如下:
其中,1.25为过剩空气系数。
3.2 风速计算
现场应用中,标准状态下的空气体积还需要转化成当前状态下的空气体积:
式中:pa—标准状态下的空气压力,Pa;
va—标准状态下的空气体积,m3;
ta—标准状态下的空气温度,℃;
pb—当前工作状态下的空气压力,Pa;
vb—当前工作状态下的空气体积,m3;
tb—当前工作状态下的空气温度,℃。
已知标准状态下的大气压为101325Pa,温度是20℃,在实际计算中,要将摄氏度转化为开尔文,即要将温度的数值加上273.15.一、二次风的空气膨胀系数计算如下:

式中:fw1—一次风与煤粉混合前的风温,℃;
fy1—一次风风管的分风压,kPa。

式中:fc1—一次风风速的理论值,m/s;
fc2—二次风风速的理论值,m/s;
S1、S2分别为一、二次风风管截面积。
3.3 含氧量计算
锅炉系统中存在许多重要参数,其中最典型的是烟气含氧量。几乎所有与锅炉相关的研究课题,都会涉及到含氧量的计算。凭借着与风煤配比的密切关系,分析锅炉的燃烧经济性时,要将其考虑进去。国内许多大型煤粉锅炉大多通过检测烟气含氧量来获知炉膛中煤粉的燃烧状况,再调整风煤配比,实现对燃烧状况的优化[6-7]。
目前,国内许多钢铁企业中,测量烟气含氧量的仪表存在以下问题:锅炉生产现场环境恶劣使得仪表运行不稳定,锅炉设备群存在信号传输延迟,造成测量不及时,锅炉不能停产而使得检修工作困难等,因此对烟气含氧量测量的优化有待进一步提高。直接测量法在测量烟气含氧量施展不开时,可以从锅炉的输入输出关系切入。因此本课题采用间接测量法来测烟气含氧量。进入锅炉的风量和煤量决定了锅炉排放的烟气含氧量,则间接测量法的关键是,获得入炉煤粉总流量和入炉总风量。通过专门设备计量入炉煤粉总流量和采用送风机的转速特性计算入炉的总风量。下面是对烟气含氧量的计算推导:

其中:V2—进入炉膛的总风量,m3;
V1—送风机的额定出力,m3;
r2—送风机的实际转速,r/min;
r2—送风机的额定转速,r/min。
将当前状态下的风体积转换为标准状态下的体积,

式中:P2—当前状态下的压力,Pa;
V2—当前状态下的体积,m3;
T2—当前状态下的温度,℃;
P0—标准状态下的压力,Pa;
V0—标准状态下的体积,m3;
T0—标准状态下的温度,℃。
煤粉燃烧所产生的总热量为
式中:Q0—输入锅炉的总热量,KJ;
F—当前煤粉的总流量,m3;
F1—煤粉中未完全燃烧煤粉的量,即除去飞灰中未燃烧的量,m3;
Qd—煤粉的低位热值,kJ/kg。
锅炉的烟气含氧量(%)为
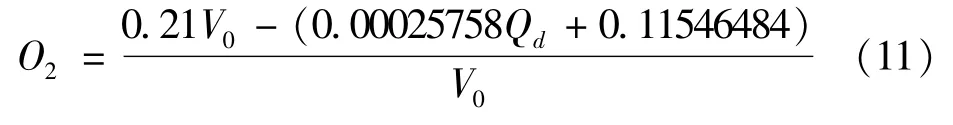
3.4 模型回归
为了保证获得的模型精确性,原始数据不光具有确定数学模型的用途,还可以用来验证所得数学模型的准确性。借助这种原理,将预处理完成的数据样本分为两部分:一部分通过最小二乘法的线性回归来建模,另一部分用来校验模型的精度,反复试验也可以降低误差的影响,不断提高所建模型的准确度。模型的建立和校验分别如图2和图3所示。
最终确定的煤粉密度与热值的模型为

其中:Qd—低位发热量,kJ/kg;
md—煤粉的密度,kg/m3。
4 燃煤锅炉的仿真
炉膛燃烧过程连续且复杂,MATLAB中的Simulink工具库,能够对线性系统和非线性系统,连续系统和离散系统等仿真分析,且便捷建模,能处理像炉膛燃烧模块中包括微分方程、差分方程等表述的动态系统。以10t/h的煤粉锅炉为仿真对象,需考虑的主要规格参数如表1所示。

图2 煤粉密度与热值模型的建立
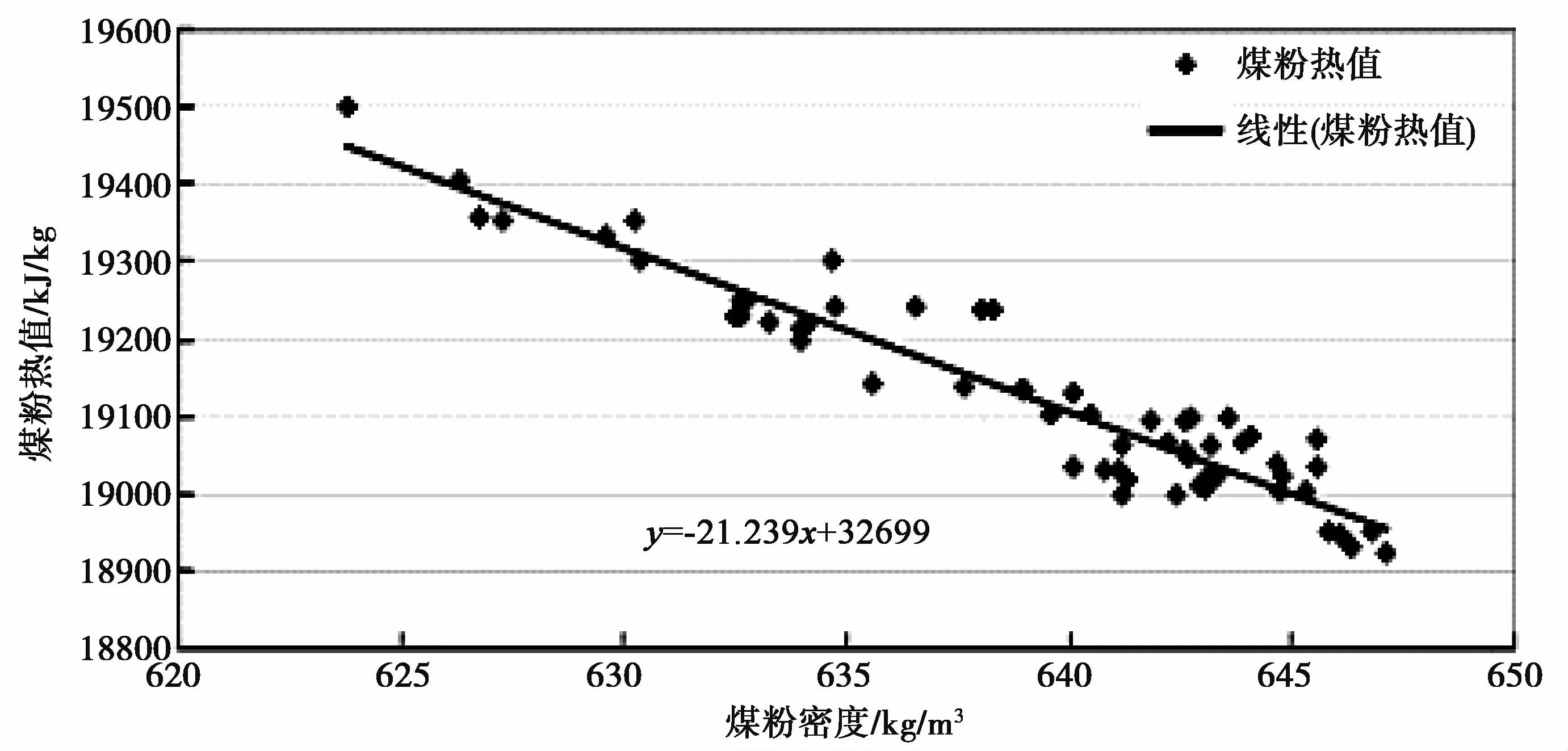
图3 煤粉密度与热值模型的验证
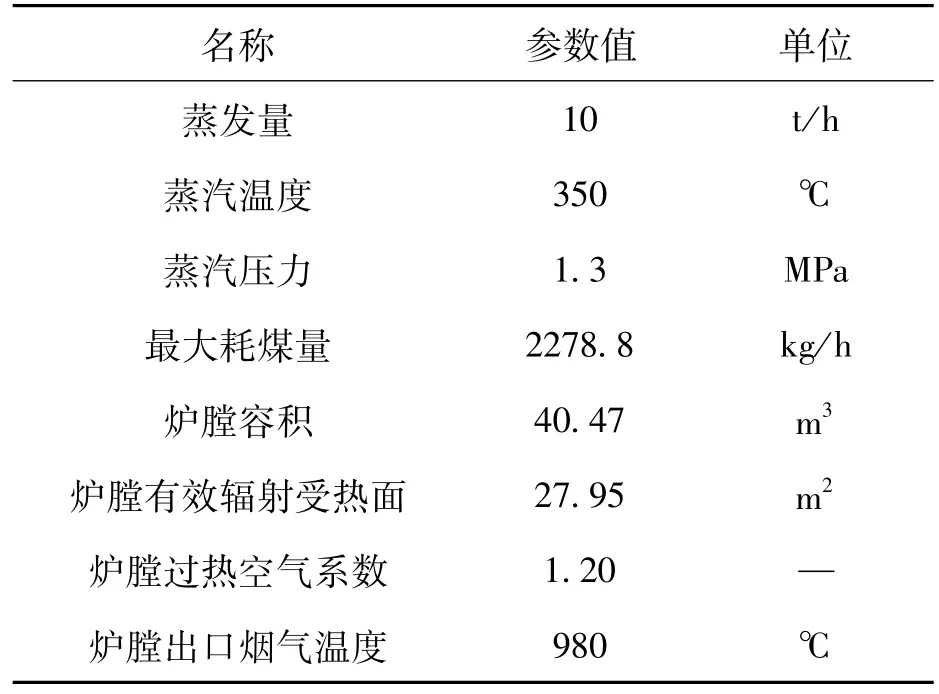
表1 锅炉相关规格参数

表2 输入输出改取值
针对炉膛燃烧模块,其输入项、状态变量项以及输出项如下(详见表2):
输入项:wc、wa、wz、ha、hz;
状态变量项:pg、(pghg)
输出项:wg、Tg、Qrad。
从仿真结果图4可以看出,炉膛出口烟气起始温度是920℃,可判断出此温度是煤粉燃烧的燃点。随着燃烧的进行,释放的热量增加,温度逐渐升高。经过一段时间后,燃烧趋于稳定,炉膛出口烟气温度稳定,稳定值为1046℃。如果更进一步分析,可以算出其中包含的排烟热损失。
5 结语
通过计算理论空气量,计算出相应的风门开度和锅炉烟气含氧量,分析了部分工况下的配风修正,最后给出煤粉计量及煤质的在线估计,建立煤粉密度与热值模型。选用 MATLAB 中的Simulink仿真工具,对炉膛燃烧模块进行仿真,得到炉膛出口烟气温度随时间变化曲线的仿真结果,结果表明具有良好的稳态性能和动态性能,为企业创造了一定的经济效益和社会效益。
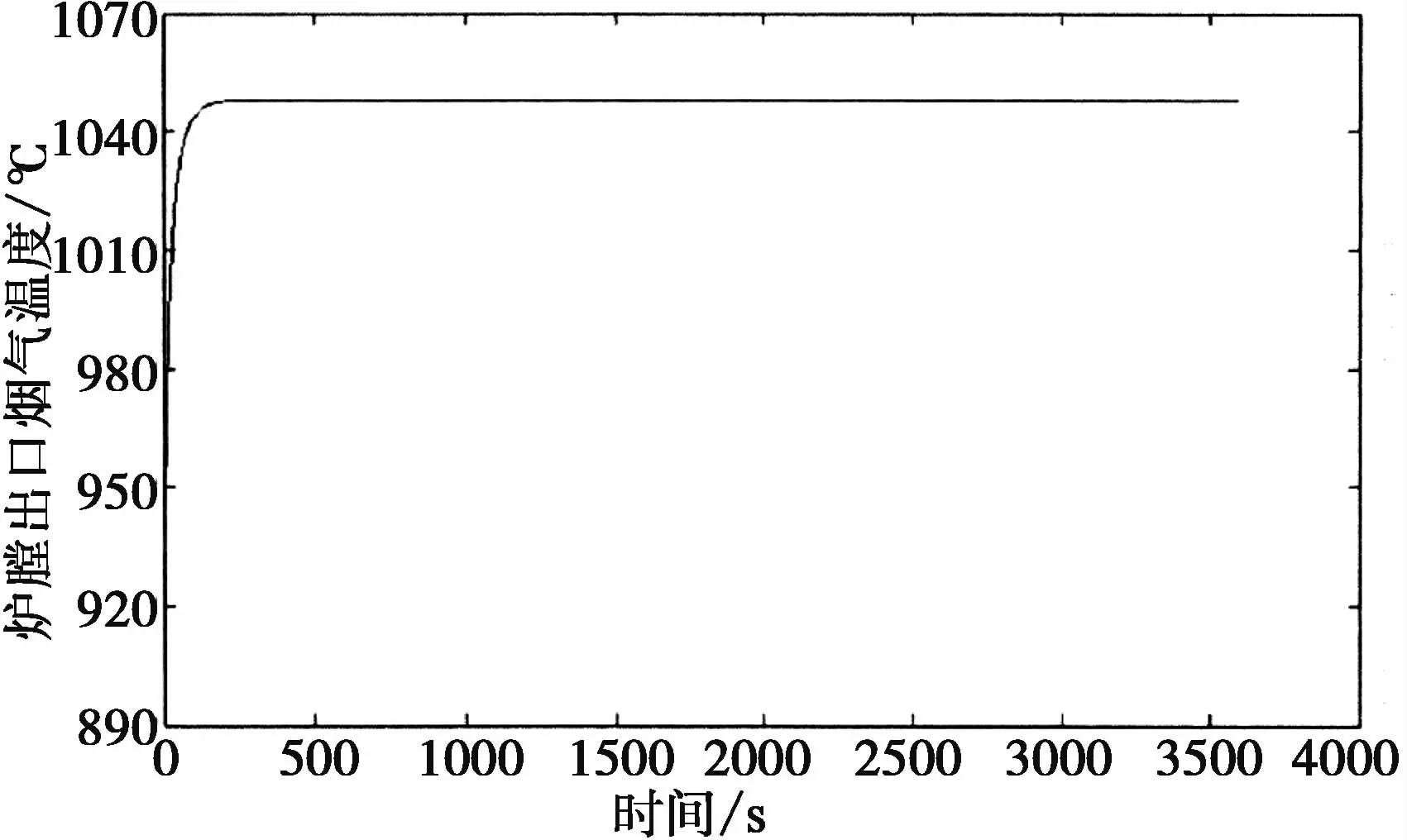
图4 炉膛出口烟气温度随时间变化曲线
