残差自回归模型在安徽省GDP预测中的应用

刘兆鹏

(宿州学院数学与统计学院， 安徽宿州 234000)

GDP是国民经济核算的重要指标之一， 它是衡量一个国家或地区经济发展和人民生活水平的重要标准， 对GDP的分析和预测已有不少结果， 但大都采用时间序列分析的ARIMA模型和灰色预测模型[1-6]. 而残差自回归模型综合了确定性分析和随机分析的优点， 既能提高拟合精度， 又便于直观解释， 用于GDP序列的分析预测， 可以取得较好效果[7-8]. 近年来， 安徽省域经济发展迅速， 发展模式也在不断优化升级， 人民收入不断增加， 已成为中部地区重要的经济体. 因此对安徽省GDP数据进行分析， 研究其变动趋势并进行短期预测， 可以为安徽省经济发展以及中部崛起战略提供必要的决策参考.

1 残差自回归模型

残差自回归模型是通过确定性因素分解法， 提取序列中的确定性信息：xt=Tt+St+εt，Tt为趋势效应拟合，St为季节效应拟合，εt为残差序列. 考虑到确定性因素分解法对信息的提取可能不充分， 需要检验残差{εt}的自相关性. 采用Durbin-Waston检验， 如果检验结果显示残差序列自相关性显著， 就需要对残差序列拟合自回归模型提取残差的相关信息， 从而提高拟合精度， 同时残差自回归模型更易于直观解释GDP序列的波动规律. 残差自回归模型如下[9]：

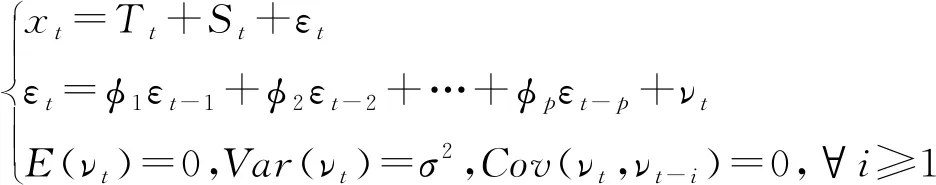
2 实证分析

2.1 数据来源

从历年《安徽省统计年鉴》获得安徽省1979年至2018年的GDP数据(表1).

根据表1， 绘制安徽省1979年至2018年的GDP时序图和自相关图(图1). 由图1知GDP呈指数上升趋势， 增长幅度逐渐加大， 且不具有周期和季节波动； 自相关图具有三角对称性， 综合判断该序列为非平稳序列.

图1 安徽省GDP时序图

表1 安徽省1979-2018年GDP数据(亿元)

2.2 模型建立与分析

鉴于GDP序列呈现出一定的指数增长趋势， 序列值之间可能存在异方差性， 所以考虑将原始时间序列取自然对数， 尽可能消除异方差性； 记取对数后序列为lnxt， 得到安徽省GDP序列取对数后的趋势图(图2). 通过观察图2可以看出， GDP对数序列lnxt蕴含显著的线性趋势， 可以建立以时间t为自变量的线性函数来提取确定性的趋势信息.

图2 安徽省GDP对数序列时序图

序列lnxt关于变量t的线性回归模型最小二乘估计SAS软件输出结果：

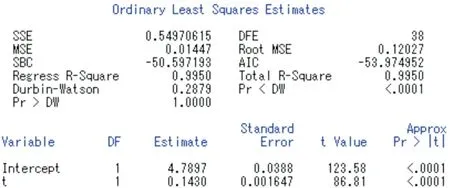
图3 普通最小二乘估计结果

输出结果显示常数项和回归系数都通过了检验， 因此趋势拟合模型有效. DW统计量的值等于0.2879， 输出概率显示残差序列显著正相关， 残差序列还蕴涵相关信息， 需要对残差序列建立拟合自相关模型.

图4 自回归残差分析输出结果

自回归残差分析结果显示残差序列具有显著2阶正相关特征， 逐步回归消除报告显示除了延迟1阶、2阶的序列值显著自相关外， 延迟其他阶数的序列值均不具有显著的自相关性， 这与残差自相关图是一致的. 残差序列的自回归模型结果为

εt=1.199086εt-1-0.475480εt-2+νt

综合上述分析可知， 对GDP对数序列lnxt建立残差自回归模型是适合的. 下图为最终拟合模型输出结果.

由图5可知， 最终拟合残差自回归模型为

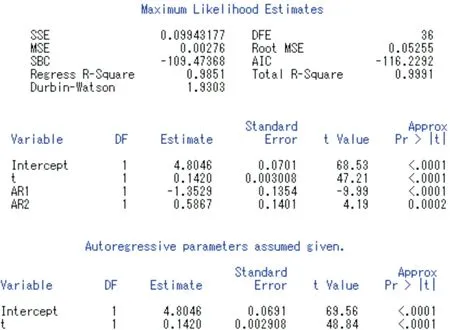
图5 最终拟合模型输出结果

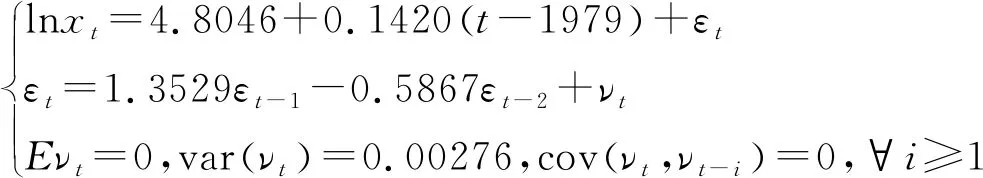
模型中所有系数都通过了显著性检验(显著性水平α=0.01)， 趋势拟合部分的R2=0.9851， 说明趋势拟合提取了GDP序列98.51%的相关信息， 整体拟合模型的R2=0.9991， 说明最终拟合模型提取了GDP数据99.91%的信息. 因此， 对GDP序列拟合残差自回归模型是显著有效的； 拟合曲线和实际数据的变动趋势更加吻合， 拟合效果见图6.

图6 趋势拟合效果图

2.3 预测与结论

利用此模型对未来3年安徽省GDP进行预测， 从预测的数据表及拟合趋势图发现， 未来3年安徽省GDP继续保持稳定增长的趋势. 并把2013年-2017年GDP的预测值与真实值比较(表3)， 发现残差自回归模型的相对误差控制在5%以内， 预测精度较高， 说明预测值比较接近真实数据， 可以为安徽省宏观经济政策的制定提供有效参考.

表3 2013年-2017年安徽省GDP预测值及相对误差

表2 安徽省未来2018年-2020年的GDP预测数据

3 结语

事实上， GDP序列是一种随机序列， 会受到居民消费、就业、固定资产投资、进出口额等诸多因素影响， 但从短期预测结果来看， 安徽省GDP在未来几年仍将处于波动增长阶段， 经济保持逐年增长势头， 人民生活水平将不断提高， 推进绿色、创新、协调发展， 加快实现文化强省、经济强省、生态强省的步伐， 确保实现全面小康社会.