一种模拟特定区域沥青短期老化的室内试验方法

冯新军，明廷军 编译

(长沙理工大学 交通运输工程学院, 湖南 长沙 410114)

1 前言

沥青和集料在拌和楼拌和过程中受高温影响会开始老化，在整个路面使用过程中，沥青经历两种完全不同的老化过程。混合、摊铺、碾压的过程经历了第一个老化过程，称为短期老化；接下来是在使用寿命期间发生的长期老化，沥青在实际路面温度下以更慢的速率继续硬化。在试验室中，设计加速老化技术，用来模拟两种老化条件下的沥青。目前通用的评价沥青短期老化的试验方法主要有薄膜加热试验(TFOT)和旋转薄膜加热(RTFOT)两种试验方法。

美国加州的Hveem于1963年提出采用旋转薄膜加热试验来代替薄膜加热试验，主要原因是基于旋转玻璃瓶中的沥青膜的厚度更接近混合料中沥青膜的厚度，到目前为止，RTFOT是最好的TFOT改进方法，能有效地模拟沥青膜的老化过程。JTG F40-2004《公路沥青路面施工技术规范》将TFOT和RTFOT等效作为沥青短期老化的评价方法。但随后的研究发现RTFOT试验也不能完全有效地评价沥青的室内老化性能。

已有几项研究验证了在各种可能条件下旋转薄膜烘箱(RTFO)测试的适用性。例如，在目前的Superpave沥青规范中，Hveem等通过分析经过RTFO测试方法老化后的沥青，来评价其抗车辙能力；Li等进行了大量试验来评价回收的沥青和使用标准试验方法(RTFO和压力老化)老化的沥青的流变性能，结果表明：回收的和试验室老化的沥青之间存在显著差异；Lee等使用RTFO老化方法研究了9种沥青的短期老化效果，然后将试验结果与现场的老化沥青样品进行比较，发现它们之间没有明显的相关性。

多年来，已经运用了各种试验设计软件和数学模型来探究这些局限性并确定在特定条件下模拟老化机理的最佳方法。寻找测试材料最佳条件的常用方法是一次只分析一个时间因素，这种方法在某种程度上是可行的，但它会消耗大量的人力、物力和时间。该文应用响应面法(RSM)来确定模拟现场短期老化的时间和温度的相应组合。RSM是一种用于设计试验、开发模型和评估试验因素的影响并优化其过程的统计方法，该方法已被有效地应用于一些沥青研究中，如表1所述。这些实例对RSM的科学支持促进了其在不同学科的应用，RSM也可以为短期老化过程的开发提供帮助。

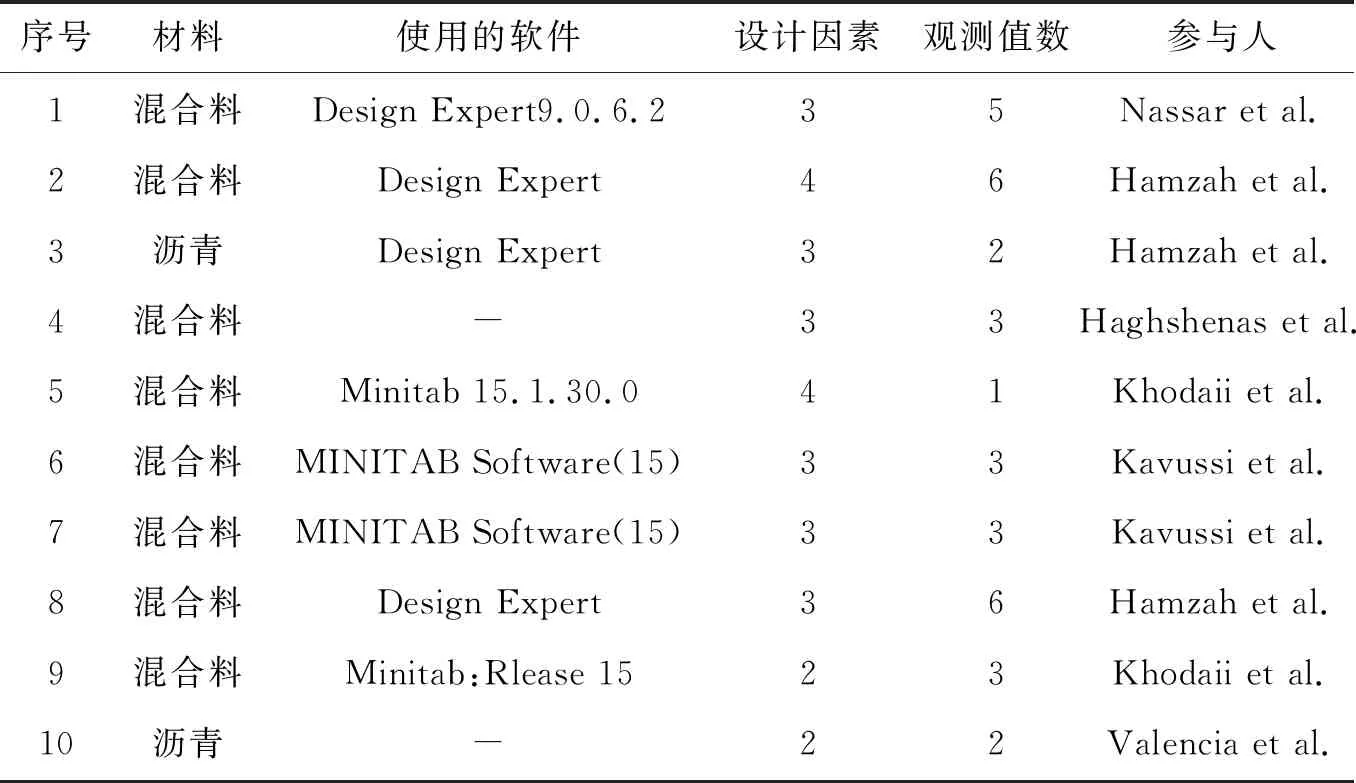
表1 RSM在沥青研究中的应用

该文提出了一种替代方法，使ASTM D2872更准确地模拟选定区域条件的人工短期沥青的老化。在该研究中，独立设计RTFOT试验的老化时间和老化温度。RSM技术用于分析试验室和现场数据的结果以及选择合适的试验室方案。根据中心组合方法设计了两个基本独立的影响因子试验方案，即老化时间和老化温度。采用软化点、针入度、64 ℃G*/sinδ和135 ℃旋转黏度作为评价指标。对所得结果进行方差分析(ANOVA)来确定沥青流变性的重要因素，使用RSM分析测试指标与老化时间和温度之间的数学关系，通过优化模型确定与现场结果相似的对应时间和温度。在这种方法中，首先定义用于选择合适时间和温度的目标值，然后根据目标值确定时间和温度的组合。RSM不仅减少了试验所需的样本数量，而且对在任何选定条件下确定沥青的短期老化性能提供了帮助。

该文首先简要介绍沥青的老化现象；其次提出一种RSM方法设计试验室短期老化方案，以模拟沥青混合料的生产实践；研究温度和时间的交互作用对沥青老化性能的影响。

2 材料和试验步骤

2.1 材料和方法

研究采用了3种不同针入度等级的沥青：来自沥青厂A的沥青80/100、来自沥青厂B的沥青80/100和沥青60/70。沥青厂A位于槟城Penanti采石场，沥青厂B位于霹雳州太平采石场。根据沥青设备的名称和沥青针入度等级(A80、B80和B60)排列沥青序号。采用沥青的针入度和软化点以及旋转黏度和车辙因子(G*/sinδ))作为评价沥青性能的指标。基于这些参数，确定试验室老化时间和温度。表2为根据ASTM D2872的原始沥青和RTFO老化沥青的流变性能。

在生产沥青混合料的同时取沥青样品，以确保沥青样品和沥青混合料中采用的沥青是同一批次，将收集的所有沥青储存在密封容器中以使沥青氧化和早期老化最小化。首先从沥青罐中收集未老化的沥青，随后，在生产之后和运输到现场之前将沥青从筒仓中收集到沥青厂。然后根据ASTM D5404标准试验方法通过旋转蒸发仪提取并回收沥青，测试回收沥青的针入度、软化点、黏度、G*/sinδ结果如表3所示。将3种未老化的沥青(A80、B80和B60)在试验室中进行不同时间和温度的短期老化试验。

2.2 试验设计

根据表4设计试验，将所有未老化的沥青在不同温度和时间的RTFO中老化。采用中心组合设计(CCD)技术评价老化变量对沥青性能的影响，CCD技术可以减少所研究的沥青总数。如表5所示，根据一些初步结果确定变量的最小和最大水平，也是RTFO可以安全处理的最大时间和温度，试验设计了时间和温度条件的9种组合。CCD不用来估算试验误差，因此，准备3个中心点重复来估计观测值建模的试验误差程度，这个试验设计的中心点对应的是163 ℃和130 min。11种老化条件的试验如表4所示，记录每个短期老化沥青的观测值。

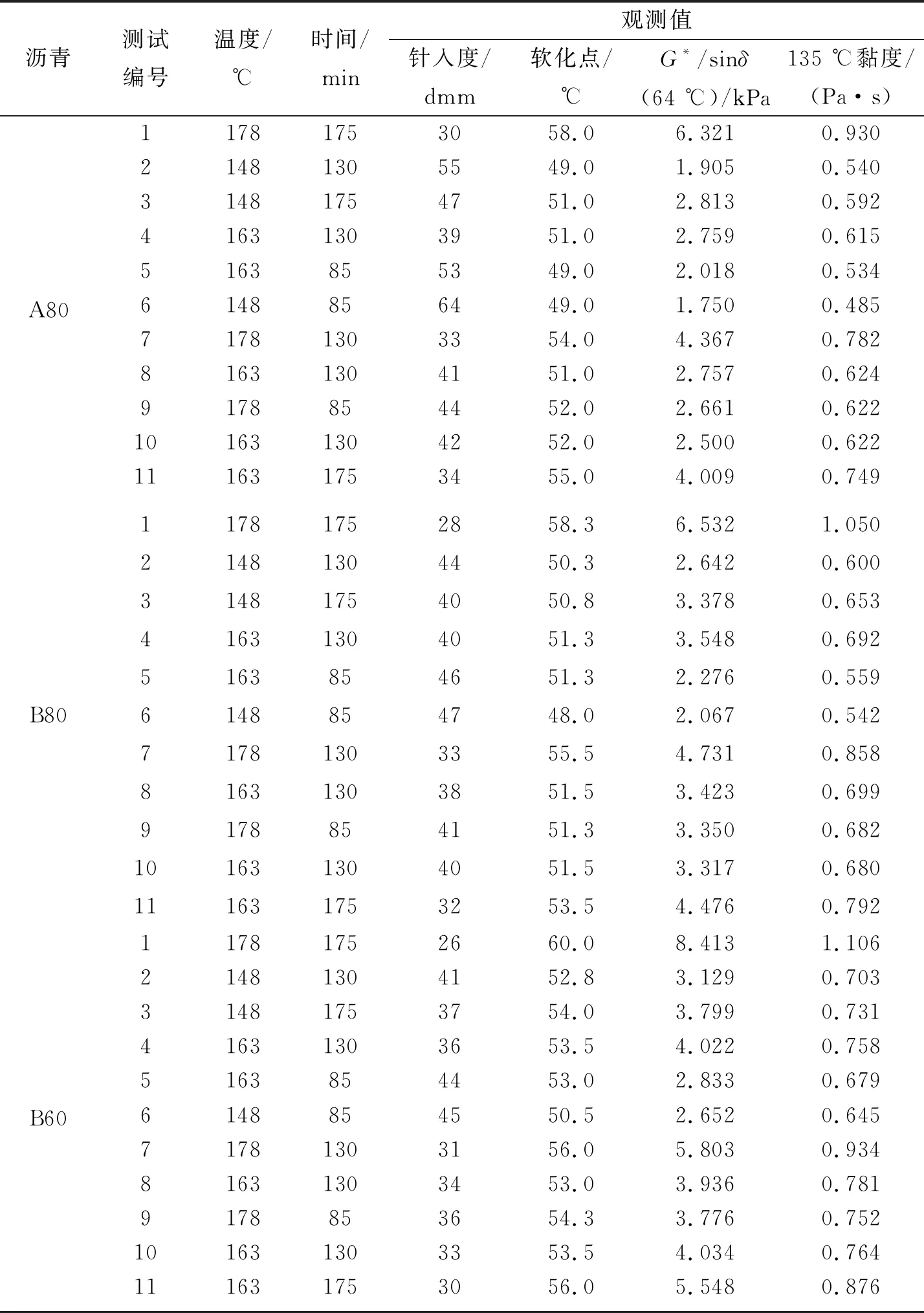
表4 试验设计

表5 调查参数水平

2.3 分析方法

采用RSM分析观测值并对每个观测值选取适当的数学模型。建模的试验区域由RTFO中龄期为85～175 min(间隔45 min)和148～178 ℃(间隔15 ℃)的沥青组成。预期的观测值可能不一定随所选变量线性变化，因此，CCD能够在二次或两因子交互模型中对预测的观测值建模。使用方差分析(ANOVA)来检验观测值中的测试因素的显著性。从模型中丢弃不重要的因素，然后，使用Design Expert 6.0.6统计软件进行图表编辑。

使用模型的预测观测值来确定时间和温度对应的组合，将试验室测试数据使用期望函数的数值优化来确定时间和温度的最佳组合，对同时满足测试指标目标值的试验因子进行了一系列优化分析。在同步优化中，每个测试指标都分配了低值和高值，然后将目标值记录到反映每个测试指标期望值的期望函数中。对于任何给定的指标，理想的范围是从0～1，1表示理想条件，0表示该值落在理想限度之外。图1为一个指标值的个体需求模型。在该研究中，为3种测试沥青及其4个观测值设计了12个单独的期望值图。在此图中，下限和上限值是每个观测值的最小值和最大值，其中值为1表示该值等于原始的沥青性能。

根据Bezerra等阐述的方法进行同步优化，所有的个体需求函数都被组合成一个整体期望值函数。如方程(1)表示总体期望值函数，目标搜索从随机起点开始并以最大斜率上升到最大值。

(1)

图1 期望函数的典型形式

式中：n为优化中包含的观测值的数量；D为总体期望值函数(各个期望函数的几何平均值)；d为观测值n的个体期望函数。

使用Design-Expert 6.0.6软件绘制总体期望值函数的三维响应曲面，并确定达到最大期望的测试参数值，然后使用建议的最佳值进行试验验证预测的最佳值。新的试验给出了可以与优化过程的预测值进行比较的实际值，原则上，预测值应与观测值相似。

3 结果与讨论

3.1 老化对针入度和软化点的影响

通常，针入度和软化点可以评估老化对沥青性质的影响，表4结果表明：对于所有类型的沥青，随着老化时间和温度的增加，针入度降低，软化点增加；且随着时间的增加，沥青变得更硬。

为了量化老化时间和温度对针入度和软化点的影响，采用F检验、失拟检验和R2对所有沥青回归模型(线性，双因子交互作用和二次方程)和拟合函数进行评价。表6、7为模型的具体数据，通过较高的R2以及失拟检验的高p值分析，沥青A80的针入度和软化点建议使用二次模型。失拟检验选择了一种不显著的失拟检验模型(Prob>F高于0.05)，该模型在F检验中也表现出可接受的低p值。类似地，分析出沥青B80和B60建议使用双因素交互作用(2FI)和线性模型。

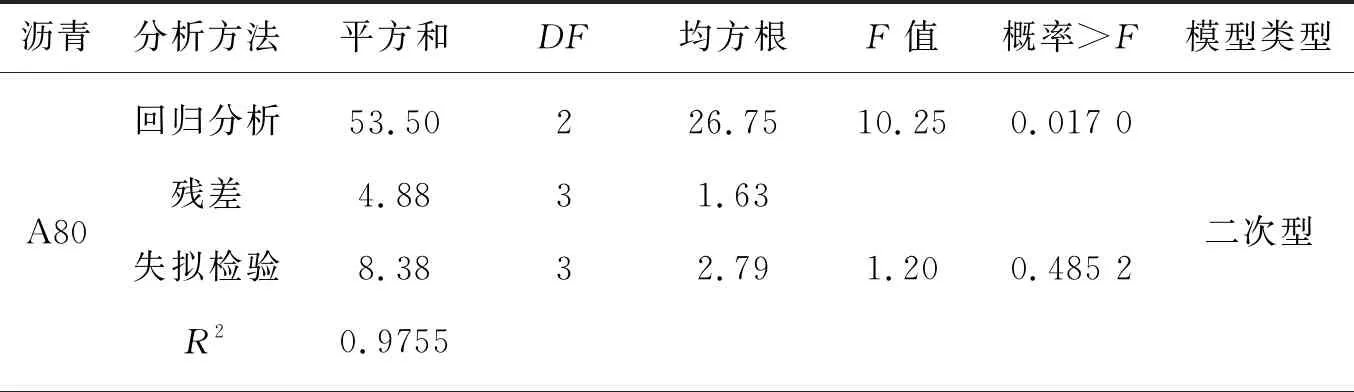
表6 基于针入度测试结果的建议模型总结

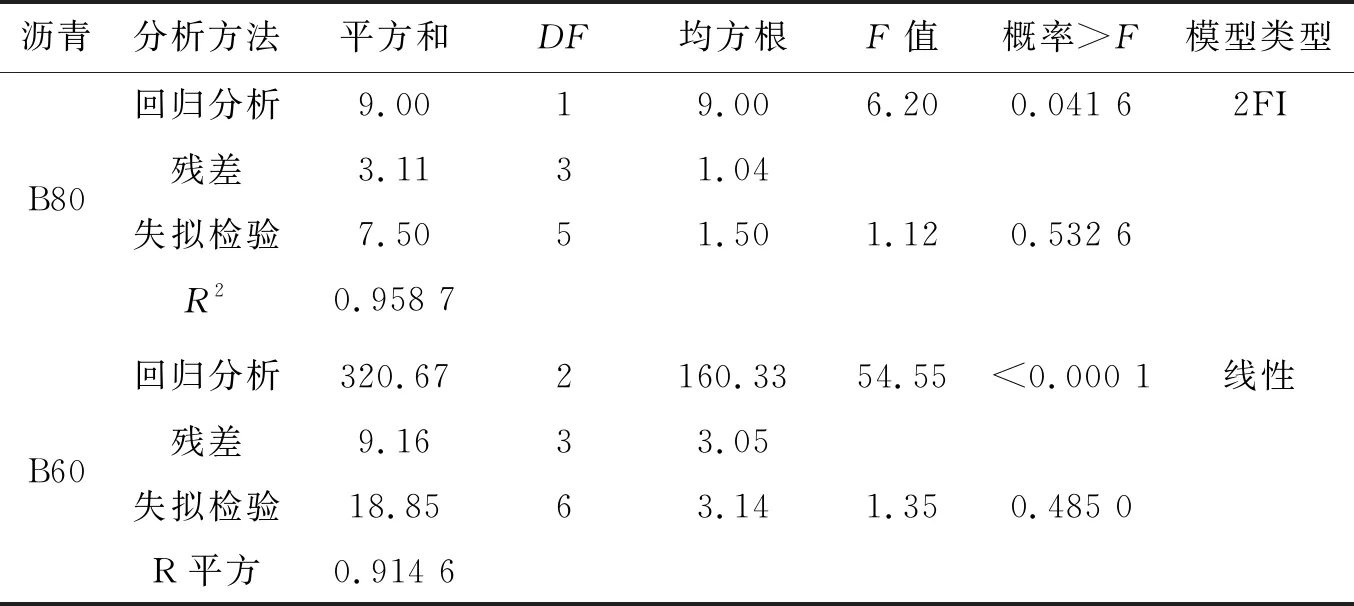
续表6

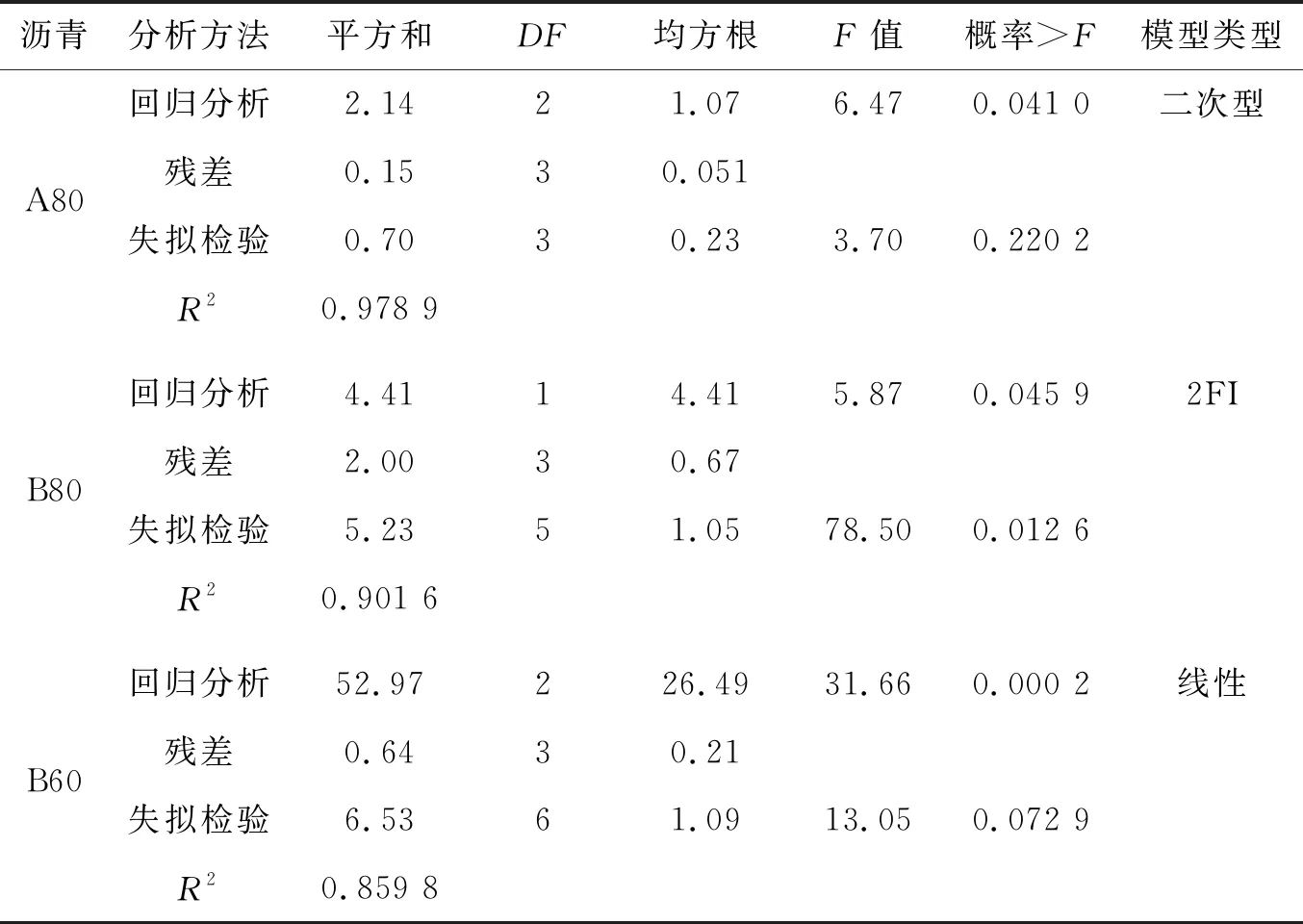
表7 基于软化点的建议模型总结

然后根据表6、7中提出的模型进行方差分析(ANOVA)，确定显著因素之间的交互作用。表8为方差分析结果。由表8中可以看出:温度、时间和温度的二阶数对测得的沥青A80的针入度有显著影响。低于0.05的“Prob>F”值表示统计学上的显著因素之间的交互作用。对于沥青B80，温度、时间以及时间和温度的交互作用是预测针入度和软化点的重要因素；对于沥青B60，时间和温度是预测针入度和软化点的唯一重要因素。

式(2)、(3)表示所提出的针入度和软化点的数学方程式。根据针入度方程中回归系数的负值，一阶时间和温度降低针入度值，而软化点升高。图2为沥青A80的等高线图，由图2可以看出时间和温度对沥青物理性质的影响。B80和B60沥青都用类似的图表示。

(2)

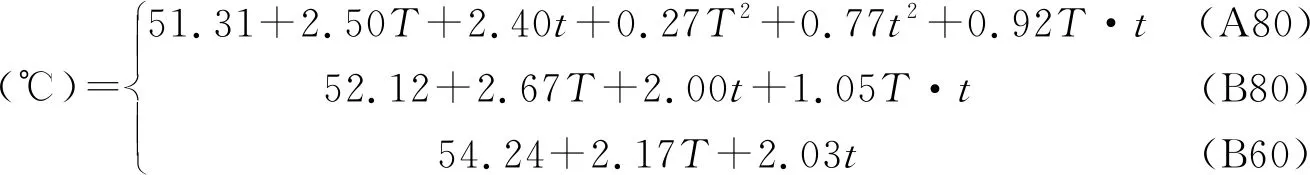
(3)

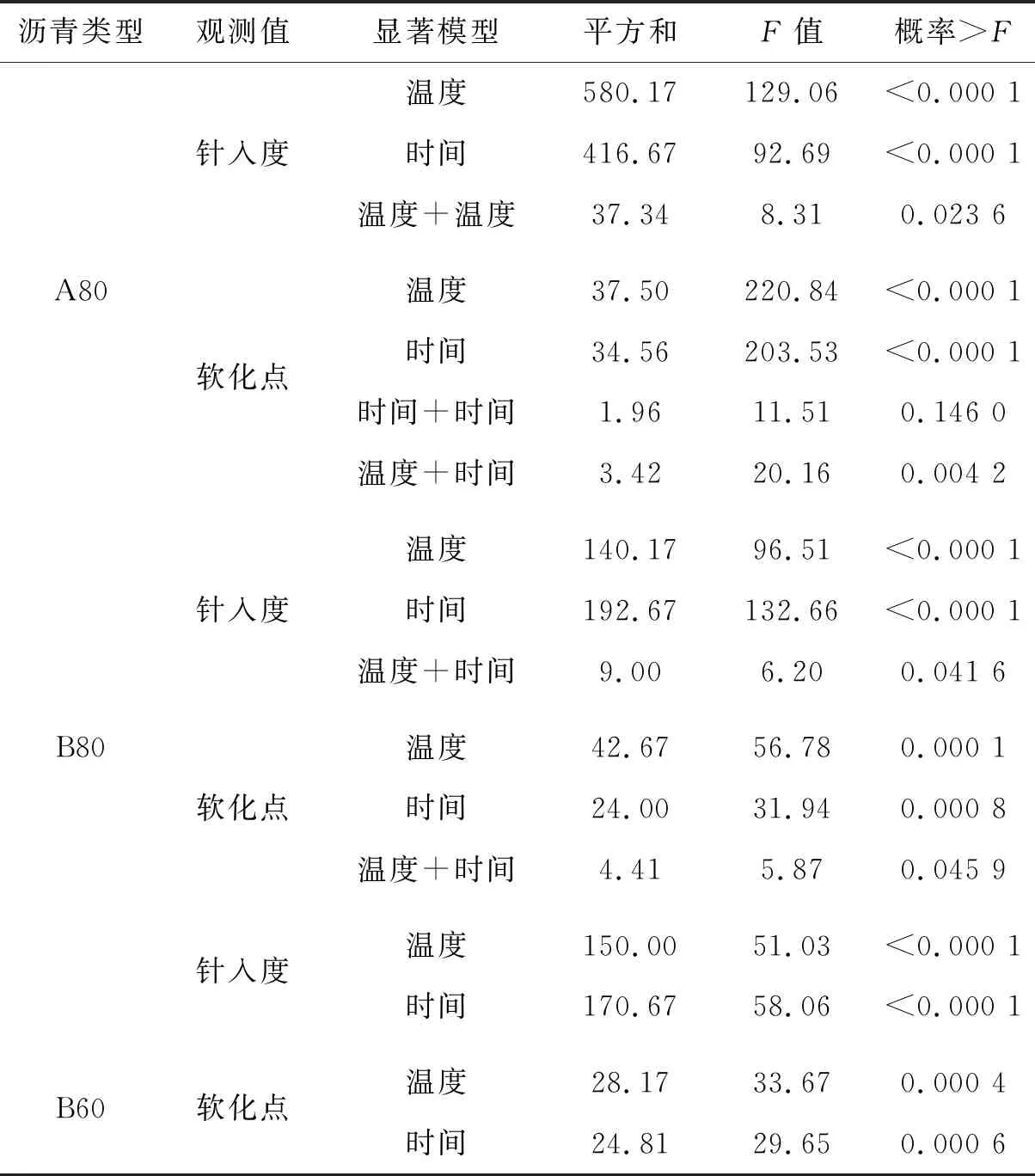
表8 基于沥青物理性质的ANOVA结果

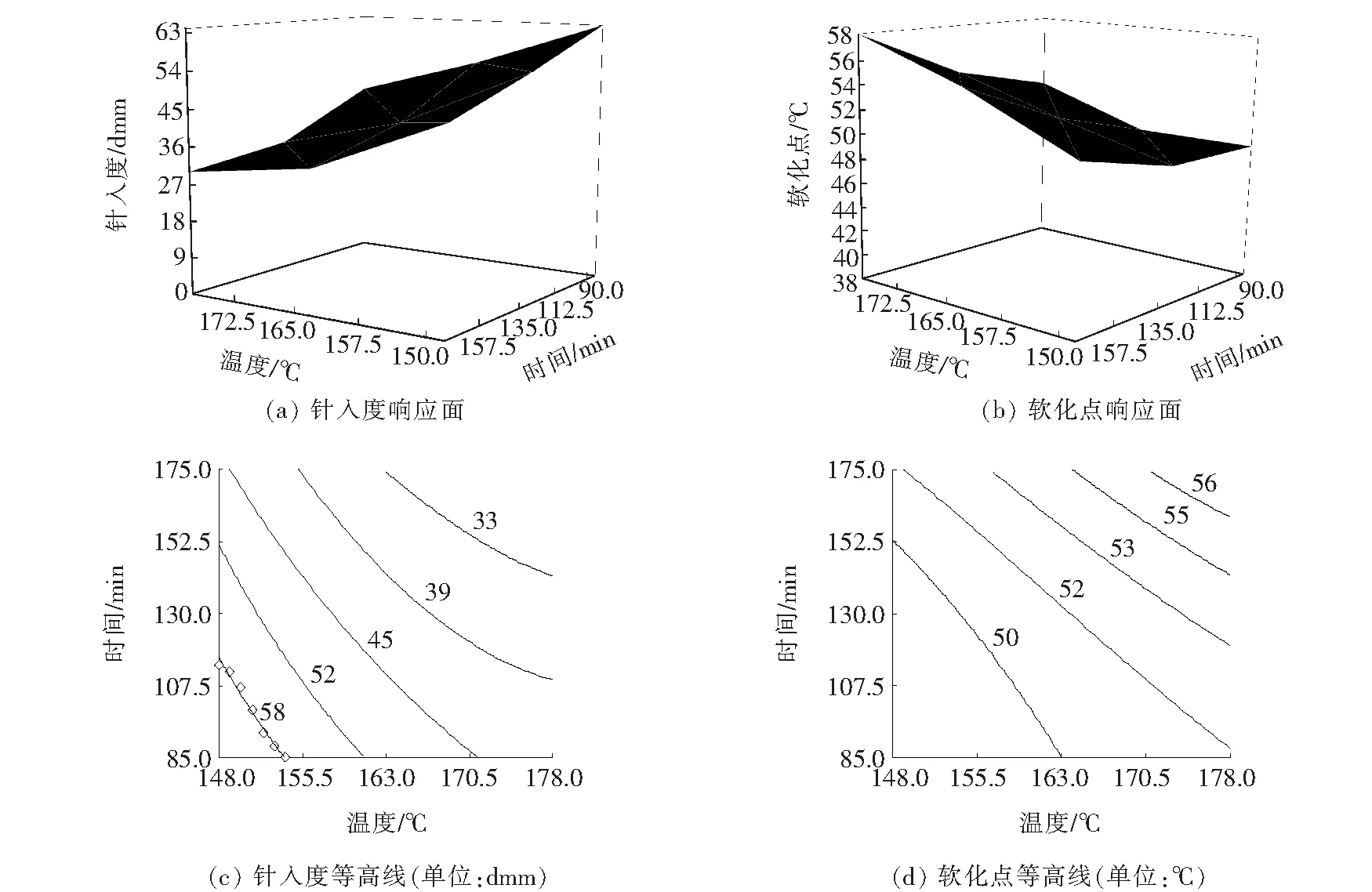
图2 沥青A80的针入度和软化点的响应面和等高线图

3.2 G*/sinδ和黏度分析

使用黏度和车辙因子G*/sinδ来评价沥青的流变性质。表4表明：当老化时间和温度升高时，G*/sinδ和黏度均增加。表9、10为预测黏度和G*/sinδ的模型，二次模型是该拟合数据的最佳方程，该模型在F检验中具有低p值，在缺乏拟合检验中具有高p值和高R2。模型的ANOVA检验结果如表11所示。由表11可以看出温度、时间、二阶温度以及时间和温度之间的交互作用对3种沥青的黏度都有显著影响。重要因素由概率>F值判断，小于0.05的概率通常认为是该参数对所检测的观测值具有显著影响的有力证据。这些因素对于预测G*/sinδ同样也是重要的。此外，二阶时间因子对预测A80和B60沥青的G*/sinδ也具有重要意义。式(4)、(5)给出了G*/sinδ和黏度的统计方程，图3为A80沥青的响应面和等高线图。从图3可以看出，随着老化时间和温度的升高，G*/sinδ和黏度增加。

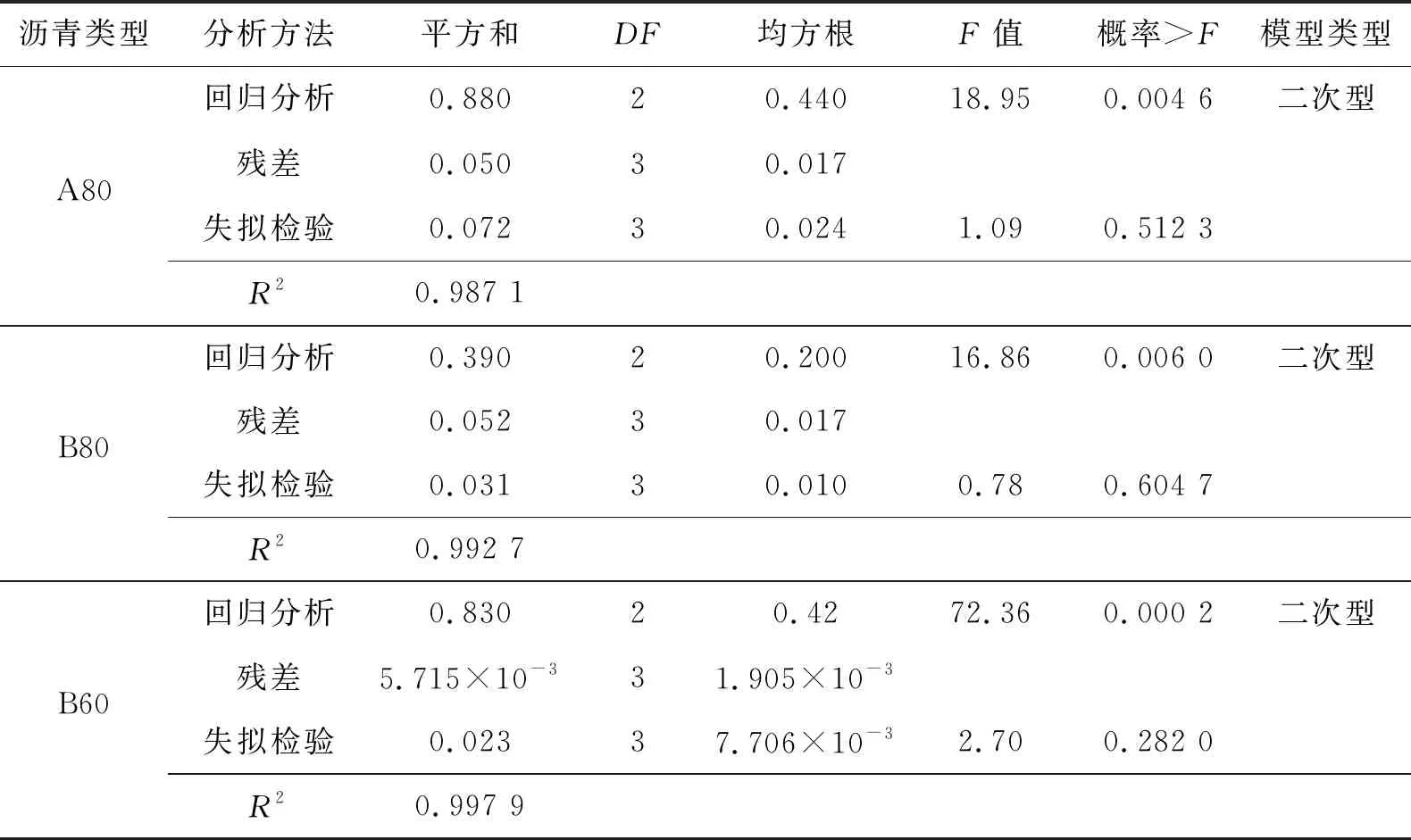
表9 G*/sinδ的模型概要

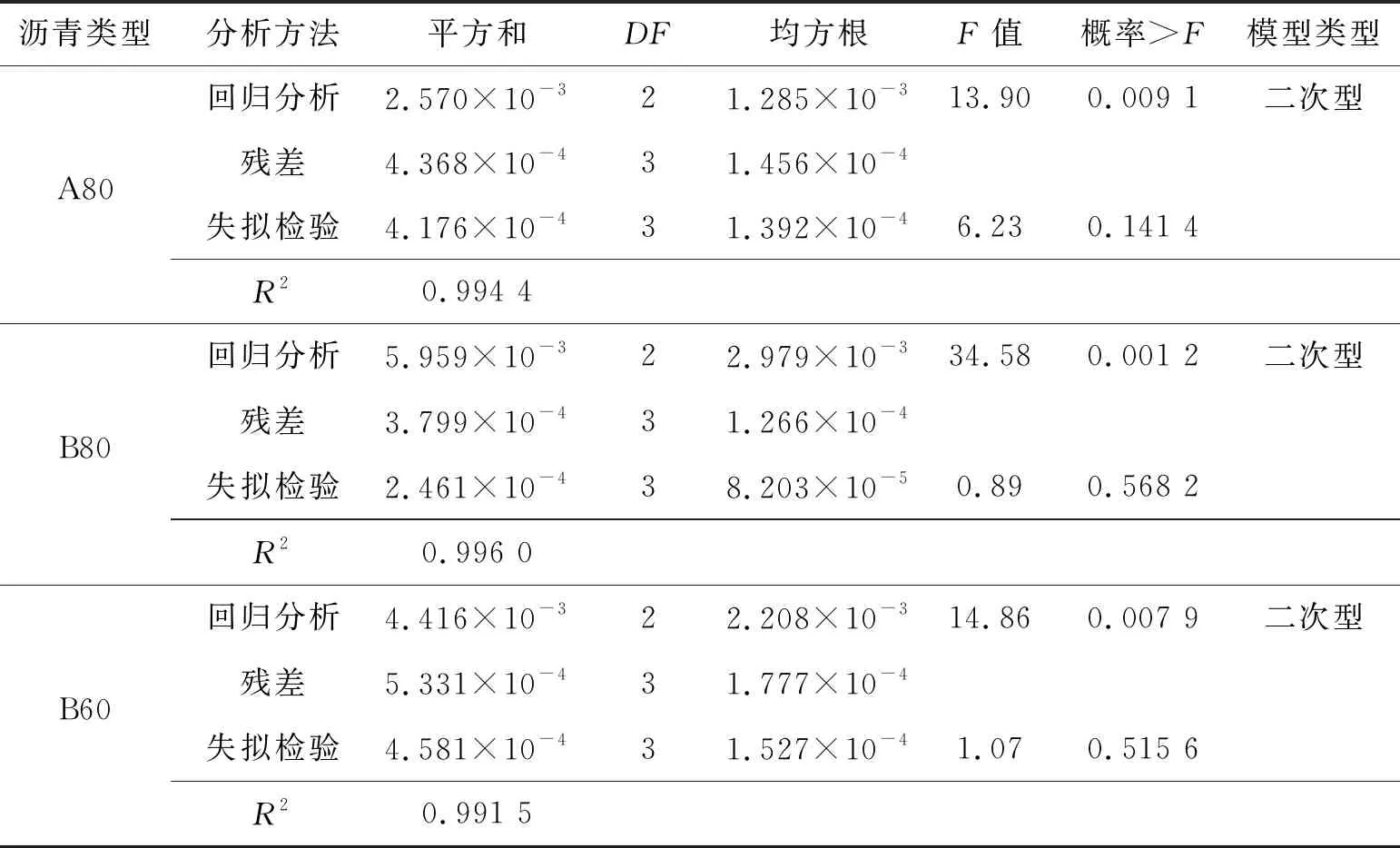
表10 黏度的模型概要

表11 基于沥青流变性质的ANOVA结果

(4)

(5)

4 优化

对同时满足每个观测值要求的因子组合进行优化分析。为了同步优化，每个目标都分配了低值和高值。在Design Expert软件中，每个观测值的目标都包含5个选项：零，最大，最小，达标和在指定范围内。如第2.3节所述，最终将目标组合成一个总体期望函数，该函数反映了每个观测值的期望范围，期望范围均从0到1，1表示理想情况，零值表示观测值落在期望范围之外。表12为该研究中选择的观测值目标和权重；表13为所提出的时间和温度组合的解决方案，即在RTFO中170 ℃下老化135 min，这些解决方案对应于现场的实际短期老化条件。表13还给出了针入度值、软化点、G*/sinδ和黏度的预测值。图4为整体期望函数的三维期望响应面，每个等高线对应于响应面的特定高度，从图4可以获得最大期望值，沥青在最优老化时间和温度下老化结果见表14，由表14可以看出：表13中的预测值与表14中的观察值非常相似。

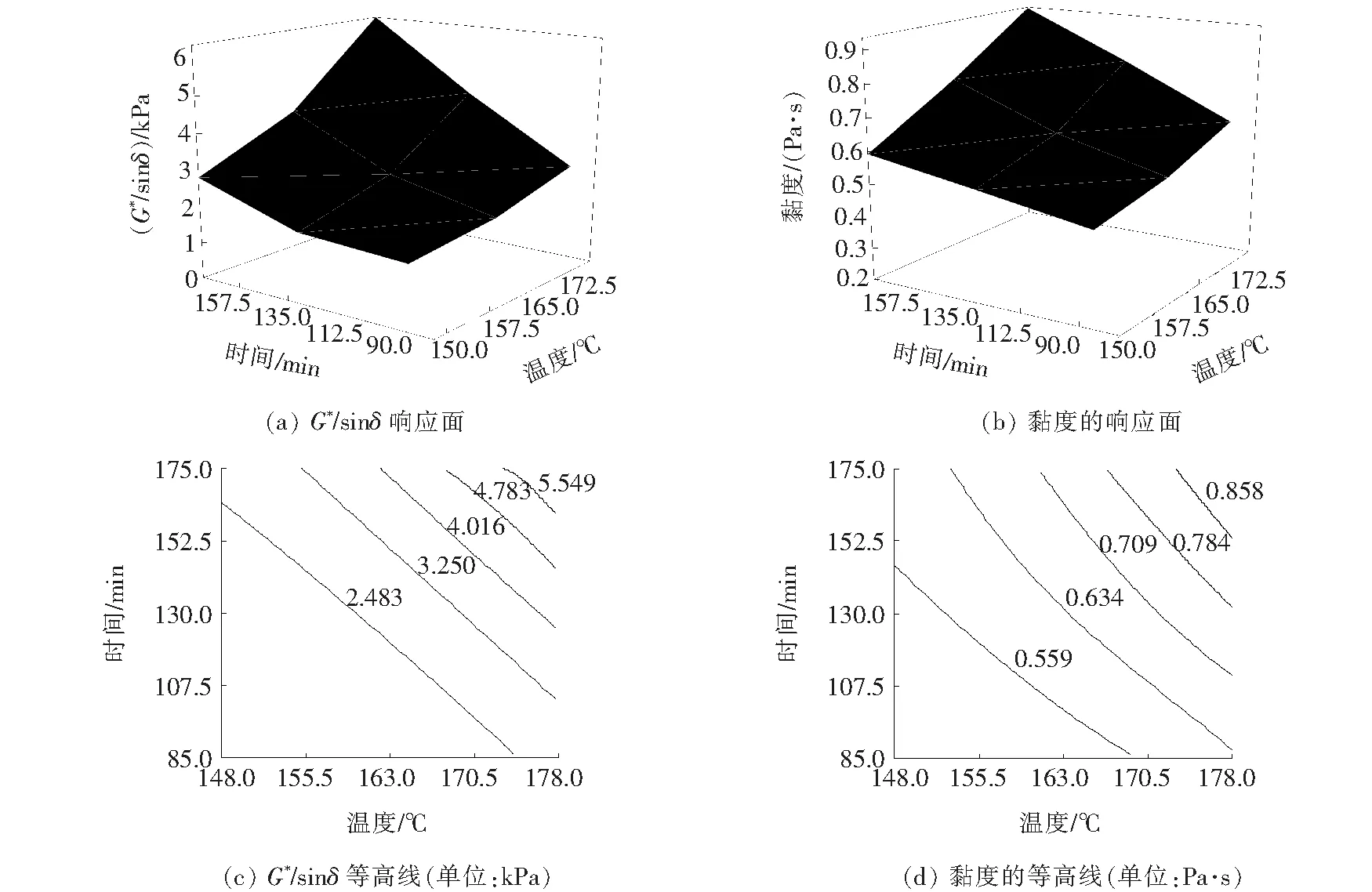
图3 A80的G*/sinδ和黏度的响应面和等高线图

表12 数值优化的选定标准，目标和权重

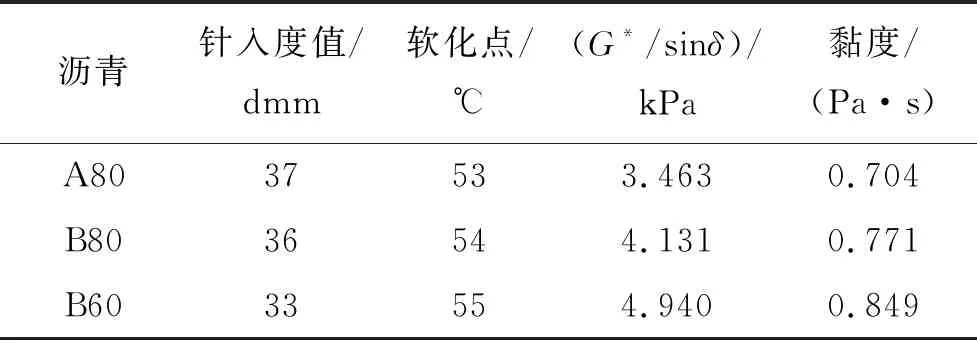
表13 基于期望性建议时间和温度组合的解决方案

期望函数会随着选择的目标不同而改变。由于流变和黏度的敏感度可能优于针入度和软化点，因此在改变G*/sinδ和黏度的权重情况下再次试验(表15)。在这种情况下，针入度和软化点的权重分配值为1，而黏度和G*/sinδ分配值为2，新解决方案(172 ℃、129 min)见表16。当指标的权重发生变化时，解决方案略有不同，这表明决策过程可能会影响到解决方案。

图4 基于温度和时间的期望等高线图

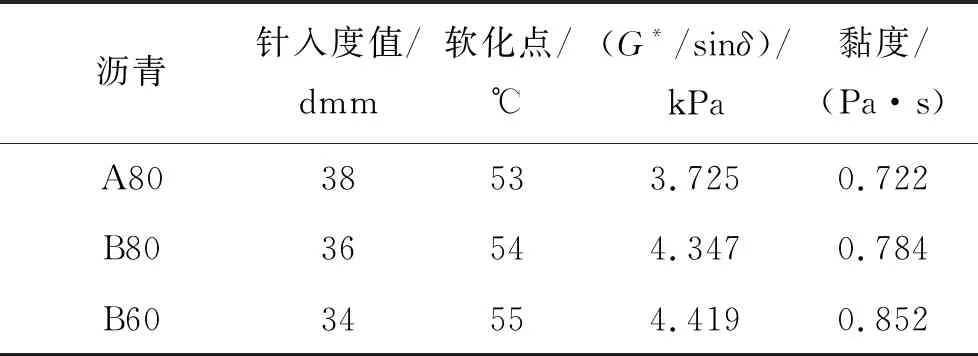
表14 验证建议的时间和温度组合

5 结论

(1) 应用RSM建立数学关系，以确定与现场实际相对应的时间和温度组合。它还可以量化不同短期老化条件下沥青的物理和流变性质，是确定选定区域条件的试验室短期老化参数的快速工具，其结果优于ASTM D2872中规定的常规时间(85 min)和温度(163 ℃)。在马来西亚选定的热带条件下，建议的温度和时间为170 ℃，持续时间为135 min。这种方法也可用于其他国家或地区。

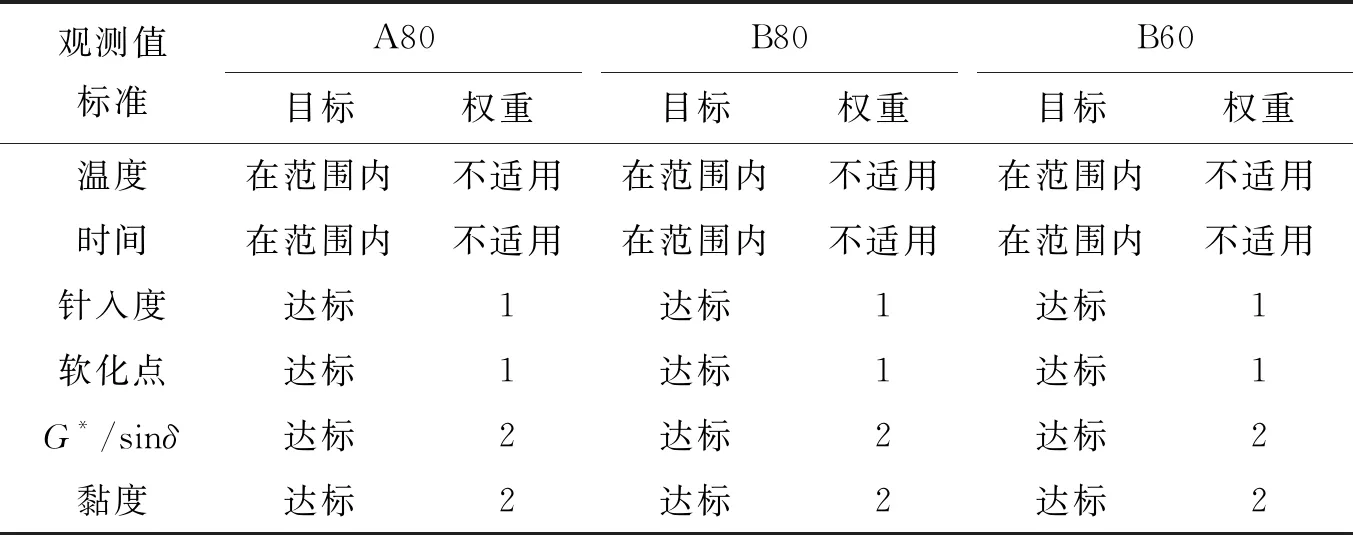
表15 数值优化的新标准选择方案

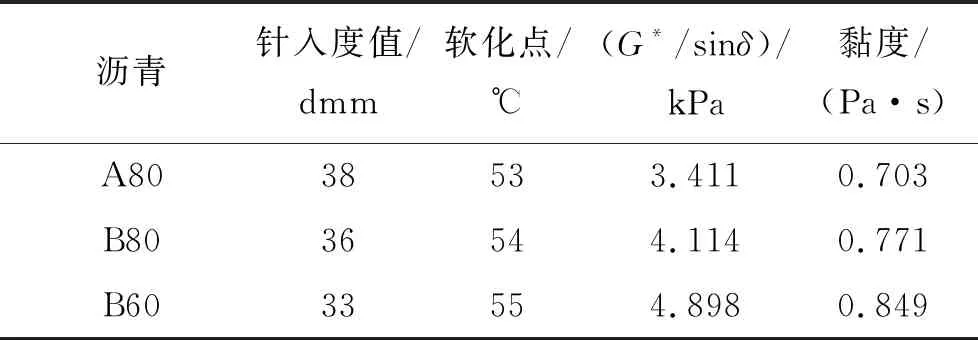
表16 新解决方案

(2) 研究表明：时间和温度是影响短期老化沥青的物理和流变性质的重要因素。当老化时间和温度升高时，沥青的软化点、G*/sinδ和黏度均增加，而针入度降低。

(3) 3种沥青都显示出Superpave参数的二次模型，包括黏度和G*/sinδ，这为沥青的经典性质提供了不同的数学方程式。沥青性能也受老化后沥青中化学成分变化的影响，评价这些变化的一种方法是使用傅里叶变换红外(FTIR)测试。该文仅探讨沥青的物理和流变性质对优化解决方案的影响，考虑到沥青的化学成分，建议使用一些化学测试，如FTIR测试，以评价老化后发生的化学变化。

——编译自：Noor Halizah Abdullah,Meor Othman Hamzah, Babak Golchin,et al.An Alternative Protocol to Artificially Simulate Short-Term Ageing of Binders for Selected Regional Condition[J].Construction and Building Materials,2018(161):654-664.