城市道路平面交叉口与隧道出口的最小间距计算

陈学信

(广西贺州市交通运输局， 广西 贺州 542899)

1 引言

随着中国经济的快速发展和城市的扩张，很多地区的城区都逐渐从平地向山地延伸，城市道路中的隧道逐渐增多。而且，由于城市道路绝大多数采取平面交叉的形式，所以不可避免地出现许多平面交叉口十分靠近隧道口的问题。中国现行的CJJ 152-2010《城市道路交叉口设计规程》、JTG D20-2017《公路路线设计规范》等都没有给出如何设置平面交叉口与隧道口之间的最小距离。为了更好地进行城市规划和城市道路建设，确保交通顺畅和行车安全，城市道路平面交叉口与隧道口之间的最小距离如何合理设置是一个比较迫切的问题。

目前，隧道多数出现在高速公路中，而高速公路的隧道以连接互通立交居多。因此，在现有文献中，研究隧道口与互通立交口之间最小距离的文献较多，而研究隧道口与平面交叉口之间最小距离的文献很少。在仅有的研究文献中，魏澜(2012年)较早地探讨了城市道路平面交叉口与隧道出口的最小安全间距，但是忽略了两个重要的因素，即识别交叉口标志的行驶距离和车辆变换车道所需的安全行驶距离，因而所得的最小安全间距严重偏低，而且未能确定交叉口车辆排队的确切距离；张弛、杨少伟和潘兵宏(2016年)考虑了车辆变换车道所需的安全行驶距离，但是对这个距离的估计过短，而且对交叉口的车辆排队距离也估计不足。为此，需要重新、科学地计算城市道路平面交叉口与隧道口之间的最小距离。

2 最小间距的划分

平面交叉口与隧道出口之间的最小距离，必须能够在不影响行车安全和道路通行能力的前提下，保证车辆在平面交叉口与隧道出口之间正常地行驶。国内外的统计数据表明：城市的交通事故60%～80%发生在平面交叉路口及其附近，因而计算平面交叉口与隧道出口之间的最小距离必须充分考虑行车安全问题。

9从行车的角度看，隧道口分为进口和出口两种类型。比较而言，从平面交叉口进入隧道容易适应，而且车流比较顺畅，交通事故也较少，所以隧道进口需要考虑的因素较少；而从隧道驶出之后司机难以适应，而且车流不那么顺畅，交通事故也较多，所以隧道出口需要考虑的因素较多。在一般情况下，只要平面交叉口与隧道出口之间的距离满足要求，那么平面交叉口与隧道进口之间的距离就必然满足要求。所以，只需要研究平面交叉口与隧道出口之间的最小距离。

如图1所示，隧道口与平面交叉口之间相隔一段距离。车辆通过平面交叉口之后，可以跟随行驶(除少量超车之外)，顺畅地进入隧道进口；而车辆驶出隧道出口之后，在到达平面交叉口之前需要处理一连串的信息，完成识别标志、变换车道、停车排队(或减速让行)等一系列动作，为此需要一段较长的距离才能确保行车安全和顺畅。根据车辆行驶的状态，这一距离通常由5段距离构成，分别是：① “明适应”距离；② 交叉口标志识别距离；③ 变换车道距离；④ 停车视距；⑤ 交叉口排队距离。在图1中，这5段 距离分别用L1、L2、L3、L4和L5表示。这里应该指出，平面交叉口分为信号控制和无信号控制两种方式，前者的安全性远大于后者，但是前者即排队通行所需的距离也大于后者所需的距离。为了长远的行车安全和信号控制起见，该文只计算信号控制的排队距离。

图1 平面交叉口与隧道出口之间的最小距离图示

在上述5段距离中，每段距离都有不同的影响因素，下文综合参考各种研究文献进行详细的分析。

3 最小间距的计算

3.1 明适应距离

所谓明适应，是指一个人由暗处到亮处，特别是强光下，最初一瞬间会感到光线刺眼发眩，几乎看不清外界事物，在经过几秒或十几秒钟之后才能逐渐看清物品。这里值得注意的是，隧道口并不是封闭的，光线从隧道口透进隧道内，其光照度与隧道纵深之间存在一种十分显著的幂函数关系，正常情况下光照度从距离隧道出口前200～300 m开始逐渐增加。因此，在正常的明适应时间——短隧道的明适应时间不超过10 s，中长隧道的明适应时间不超过13 s，驾驶人在到达隧道出口时已经基本完成了明适应。考虑到这一因素，车辆在无灯光的情况下驶出隧道时，驾驶人的明适应时间只需1～3 s，可取中间值即2 s。

其次，高速公路的隧道一般都有行车速度限制，通常为设计行车速度的80%。但是在城市道路中，由于设计行车速度较低，隧道的行车速度通常与设计行车速度相同。于是在不同的行车速度下，明适应距离的计算公式为:

(1)

式中：L1为明适应距离；V为设计行车速度；t1为明适应时间。

按式(1)和2 s的明适应时间计算所得的明适应距离(取整为5的倍数，下同)如表1所示。

表1 隧道外明适应距离

3.2 交叉口标志识别距离

车辆驶出隧道之后，驾驶人需要及时地识别前面的交叉口标志并做出判断，为此必需一定的识别视距。所谓识别视距，是在一定速度下，确保驾驶人可以清楚辨认标志并作出决策的距离。根据研究，识别视距的计算公式为：

(2)

式中：L2为交叉口识别距离；H为标志与小客车驾驶人视线的高差；t2为识别标志的反应时间；B为驾驶人视点至单悬臂标志中间的距离；θ为驾驶人视野角度。

一般而言，识别标志的反应时间为2.7 s。其次，小客车驾驶人视线的高度为1.2 m，而标志的高度通常为5.5 m(等于机动车最小净高4.5 m加1 m)，故两者的高差H为4.3 m。再其次，该文按单向双车道计算——因为单洞隧道通常为单向双车道，驾驶人视线至单悬臂标志中间的距离约等于一条车道宽度，故B取3.5 m。最后，驾驶人的视轴移动5°时，识别标志的效果最好，故θ取5°。由此得到的标志识别距离如表2所示。

表2 交叉口标志识别距离(单向双车道)

3.3 变换车道距离

城市道路通常为单向双车道或多车道，车辆为了进入预定的路线经常要变换车道，因此必须考虑一次或多次变换车道所需的时间和距离。该文研究单向双车道的情形，因此只考虑一次变换车道所需的距离。

在快速行车的情况下，变换车道距离由3部分组成：① 等待可插入间隙的行驶距离；② 判断可插入间隙的反应距离；③ 横移车道所需的调整距离。一些研究者认为，城市道路的行车速度较低，驾驶人可以减速行车甚至停车等待插入间隙，所以可以只考虑横移车道所需的调整距离。这一观点有可取之处，但是它的缺陷也是明显的，因为无论驾驶人是减速行车还是停车，显然都需要一段距离。一般而言，驾驶人可以在等待可插入间隙的同时判断可插入间隙，而不会将等待与判断这两种行为分割开来，所以判断可插入间隙的反应距离可以省略。故只需考虑两段距离：① 等待可插入间隙的低速行驶距离；② 横移车道所需的调整距离。在等待可插入间隙的等待时间内，车辆一直以等待变换车道的低速行驶，达到平均等待时间之后就会进行插入，这个过程的行驶距离为：

(3)

式中：L′3为等待可插入间隙的行驶距离；t′3为等待可插入间隙的行驶时间或平均等待时间；Vw为等待可插入间隙的行车速度，通常为正常速度的85%即Vw=85%V。

在3级服务水平的条件下，车头时距服从二阶埃尔朗分布。于是根据二阶埃尔朗分布函数，可将等待可插入间隙的平均等待时间的计算公式表示为：

(4)

式中：t为车辆临界间隙时间，取3.5 s；λ为车辆的平均到达率，λ=Q/(3 600n)，其中Q为设计通行能力(即3级服务水平的最大服务交通量)，n为车道数，该文取n=2；τ为最小车头时距，一般为1.0～1.5 s，通常取1.2 s。

按照CJJ 37-2012《城市道路设计规范》的设计通行能力，计算了各种行车速度下的平均等待时间如表3所示。

表3 平均等待时间(单向双车道)

车辆在横移车道的行驶过程中，通常需要将速度增加到正常的甚至更高的水平以便保持行车安全距离，因而横移车道的行车速度在整体上可按设计行车速度来计算。则变换车道所需的距离为：

(5)

式中：L3为变换车道距离；L″3为横移车道所需的调整距离；t″3为横移车道所需的调整时间。

根据现有的研究，车辆在各种行车速度下变换一个车道需3～4 s的时间，相应的横移速度约为1 m/s。于是在大部分车道宽度为3.5 m的情况下，横移车道所需的时间约为3.5 s。经计算，变换一次车道所需的距离如表4所示。

3.4 停车视距

变换车道之后，车辆应该维持一段自由行驶的安全距离，这个距离在高速公路上通常为100 m。不过，

表4 变换车道距离(单向双车道)

城市道路的行车速度比高速公路低得多，所以应按照不同的设计行车速度来计算这段减速行驶距离。而在最不利的情况下，由于前面就是排队车辆的队尾，车辆并不能进行自由行驶，只能采取紧急停车的方式，因而需要计算一个停车视距。

停车视距分为反应距离和制动距离两部分，其计算公式为：

(6)

式中：L4为停车视距；t4为驾驶人的反应时间，通常为1.5 s；g为重力加速度，取9.8 m/s2；f为路面与轮胎之间的摩阻系数，一般按路面处于潮湿状态考虑，水泥混凝土路面取0.5，沥青混凝土路面取0.4。

按摩阻系数较小的沥青路面来计算，停车视距如表5所示。

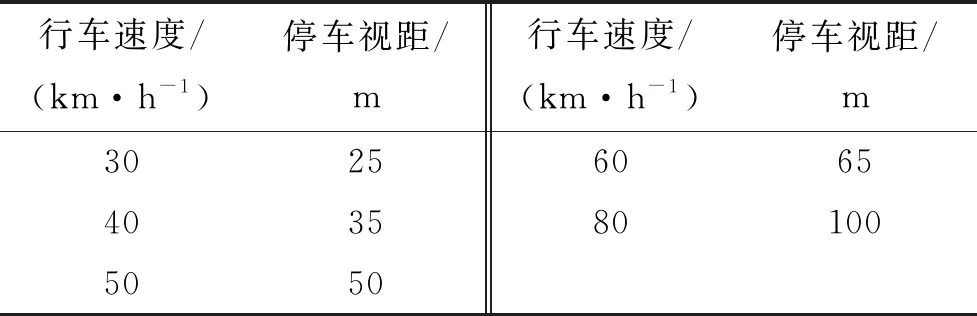
表5 停车视距(沥青路面)

3.5 交叉口排队距离

根据GB 50647-2011《城市道路交叉口规划规范》，交叉口的设置主要有4种情形：停车让行、减速让行、全无管制和信号控制，其中停车让行和信号管制所需的距离相对较大。考虑到主要的城市道路迟早都会采取信号管制的方式，所以只计算信号管制所需的车辆排队距离。

对于特定的交叉口而言，车辆排队距离与平均交通量、饱和交通量、信号周期时长、红灯时间、车身长度等因素有关，需要通过观测来计算。但是对于通用的交叉口来说，可以参考现有的研究，通过经验来获得车辆排队距离。现有的研究大多采用排队车辆为6辆，每辆车长9 m来计算，得到排队距离均为54 m。这样的计算显然难以满足安全行车要求，因为它只相当于15 s的设计交通量(表6)。应该指出，城市道路交叉口的设计行车速度通常为相交道路设计行车速度的50%～70%，但是排队的车辆都是按照相交道路的设计行车速度驶来的。根据美国马里兰州的研究，城市道路信号控制交叉口的临界交通量可以达到1 800 pcu/h，因而信号控制交叉口不会影响(80 km/h及以下)城市道路的设计通行能力，只考虑红灯所造成的排队车辆即可。在一般情况下，信号的周期时长为30～120 s，相应的一条道路的红灯时间为15～60 s，平均为37.5 s。考虑右转车辆的分流，可以按照80%的设计交通量——转换为80%的平均红灯时间计算，也就是将30 s的设计交通量作为排队车辆数量。则交叉口排队距离为：

L5=9N30 s

(7)

式中：L5为排队距离；N30 s为30 s红灯时间的设计交通量即排队车辆，取整数。

按照表6的30 s设计交通量，得到交叉口的排队距离如表7所示。

表6 交叉口一条车道停车数量

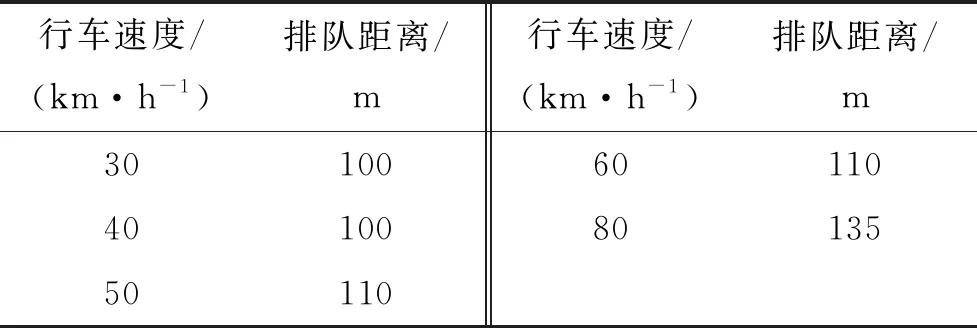
表7 交叉口排队距离

3.6 最小间距及其分析

综上所述，可以得到单向双车道城市道路的平面交叉口与隧道出口之间的最小距离如表8所示。在表8中，列出了两个类似的研究结果以便进行比较。

由表8可知：与该文的计算结果相比，文献[1]计算的最小距离严重偏低，而文献[2]计算的最小距离也显著偏低。究其原因，主要是文献[1]没考虑标志识别距离和变换车道距离，而文献[2]没考虑等待可插入间隙的低速行驶距离，对排队距离也估计不足。在该文的计算中，变换车道和排队的距离相对较长，而这两段距离往往存在较大的不确定性，较长的距离可以更好地保证行车安全。

表8 平面交叉口与隧道出口之间的最小距离(单向双车道)

例如，H市新建一条环城道路，采用四车道Ⅰ级公路标准，设计行车速度为80 km/h。因为地形限制，该路设置了一条中隧道，隧道出口距离最近的平面交叉口只有约420 m的距离。按照表8的标准，420 m的距离似乎不满足平面交叉口与隧道出口之间的最小距离即530 m。但是考虑到该路按照Ⅰ级公路标准建设，可以参照公路的通行做法，将隧道与平面交叉口之间的速度限制为设计行车速度的80%即60 km/h，如此便可满足最小距离即385 m的要求。

4 结语

该文全面地分析和计算了单向双车道城市道路的隧道出口与平面交叉口之间的最小距离，所得的结果可作为城市规划、城市道路建设和管理等方面的可靠依据。当然，为了确保这些最小距离的行车安全和交通顺畅，在实际建设和管理中应该增加交叉口的左转或右转专用道，加强行车速度限制和信号设置，尽量缩短隧道出口方向的交叉口车辆排队长度。