基于MLP的高速公路服务区合理规模测算模型

张艳秋, 陈坚, 杨林

(1.招商局生态环保科技有限公司, 重庆市 400067;2.重庆交通大学 交通运输学院；3.重庆大学 建筑城规学院)

1 前言

服务区作为高速公路上的“驿站”和“窗口”，是高速公路安全、便捷、舒适出行的保障，发挥着重要作用。在中国高速公路连线成网加快发展的新时期，服务区作为高速公路系统的重要组成部分也逐渐发展起来，截至2018年底，中国高速公路服务区数量达到2 850对左右。但中国服务区在发展和建设中存在诸多问题，普遍存在服务区征地面积及建设规模与主线交通量不相符的现象，缺乏对服务区进行系统定量分析预测和建设规模可行性研究。

国内外对高速公路服务区的研究宏观上主要为服务区功能定位、规划布局，微观层面主要为服务区服务水平评价、驶入率预测等，近年来学者们对服务区规模相继展开了研究。现有对服务区规模的研究大多从服务区物理设施及驶入率入手，通过驶入率计算服务区的停车场面积，再定性分析停车场面积与服务区面积之间关系，参数取值经验性居多，对服务区合理规模与其影响因素之间定量关系的研究较少，缺少反映客观规律的模型；且现有对服务区消费行为的研究较少，服务区规模研究中也尚未考虑出行者消费行为因素，消费行为对规模的影响未得到充分重视。该文在分析服务区合理规模影响因素时充分考虑出行者消费行为及其他交通参数，构建基于MLP的合理规模测算模型，并用实例进行验证。可为当前服务区规划设计、升级改造发展提供参考依据。

2 合理规模界定及影响因素

2.1 合理规模界定

服务区根据其所处地理位置、周边资源开发、吸引人群的不同，其服务区功能设置、规模大小应有所区别，服务区规模的设置与服务区经营效益、对客流的吸引力及服务水平紧密相关。服务区合理规模即在一定经济发展水平下，服务区用地面积及功能设置与主线交通量、驶入率、服务区功能定位、出行者消费需求相匹配，能最大程度上满足出行者的需求。

2.2 合理规模影响因素

根据高速公路服务区现有配置可知其总体规模由以车为服务对象的停车场、加油站、车辆维修中心，以人为对象的房建区及道路规模，以及绿化及其他规模构成。房建区及道路规模主要包括厕所、餐厅、商店、住宿休息区、附属设施等，该部分是服务区主体构成部分，是服务区运营的核心。

高速公路服务区规模的影响因素众多，包括服务区地理位置、功能定位、主线断面交通量、驶入率、车型结构、出行者消费行为等，只有明确影响服务区合理规模的主要因素，才能进行合理规模研究。根据相关研究综合分析拟定主线断面交通量、驶入率、高峰率、周转率、车型结构、消费行为作为影响合理规模的6大主要因素。各影响因素含义如下：

(1) 主线断面交通量 ：指一定时期内通过服务区截面的交通量(双侧)，单位：(pcu/d)。

(2) 驶入率：驶入到服务区的交通量与主线交通量的比值。

(3) 高峰率：指在高峰时段停留的车辆数(pcu/h)与每天停放车辆数(pcu/d)的比值。

(4) 周转率：指服务区的一个停车位在1 h内被使用的次数。

(5) 车型结构：驶入服务区大型车与小型车的比值。

(6) 消费行为：包括同行人数、消费水平、消费需求等，消费水平和消费需求分别用实际消费金额(元)和服务区平均消费需求项(项)量化表示。

各因素与服务区总体规模影响关系见图1。

图1 因素与服务区总体规模影响关系

3 深度学习相关理论

3.1 深度学习概述

深度学习是新兴的机器学习研究领域，是当前人工智能的研究热点，旨在研究如何从数据中自动地提取多层特征表示，其核心思想是通过数据驱动方式，采用一系列的非线性变换，从原始数据中提取由低层到高层、由具体到抽象、由一般到特定语义的特征。通过从多源异构数据中进行自动特征学习，从而将不同数据映射到一个相同的隐空间，能够获得数据的统一表征。目前已在图像识别、语音识别、自然语言处理、车牌定位等领域展现出了巨大的优势。

深度学习常用模型有多层感知机(MLP)、受限玻尔兹曼机(RBM)、深度置信网络(DBN)、卷积神经网络(CNN)、循环神经网络(RNN)、自动编码机(AE)等。常用软件工具平台主要有TensorFlow、Caffe等，操作语言主要为C++、Python、Matlab。深度学习常见模型及特点见表1。

3.2 MLP神经网络

(1) 模型结构及预测原理

MLP(Multi-Layer Perception-多层感知机)属于前馈深度神经网络模型，网络结构由输入层、隐含层、输出层组成，隐含层根据需要由一层或多层组成。MLP可被看作一个有向图，由多个节点层所组成，每一层都全连接到下一层，除了输入节点，每个节点都是一个带有非线性激活函数的神经元，常采用误差反向传播算法(BP算法)进行训练。

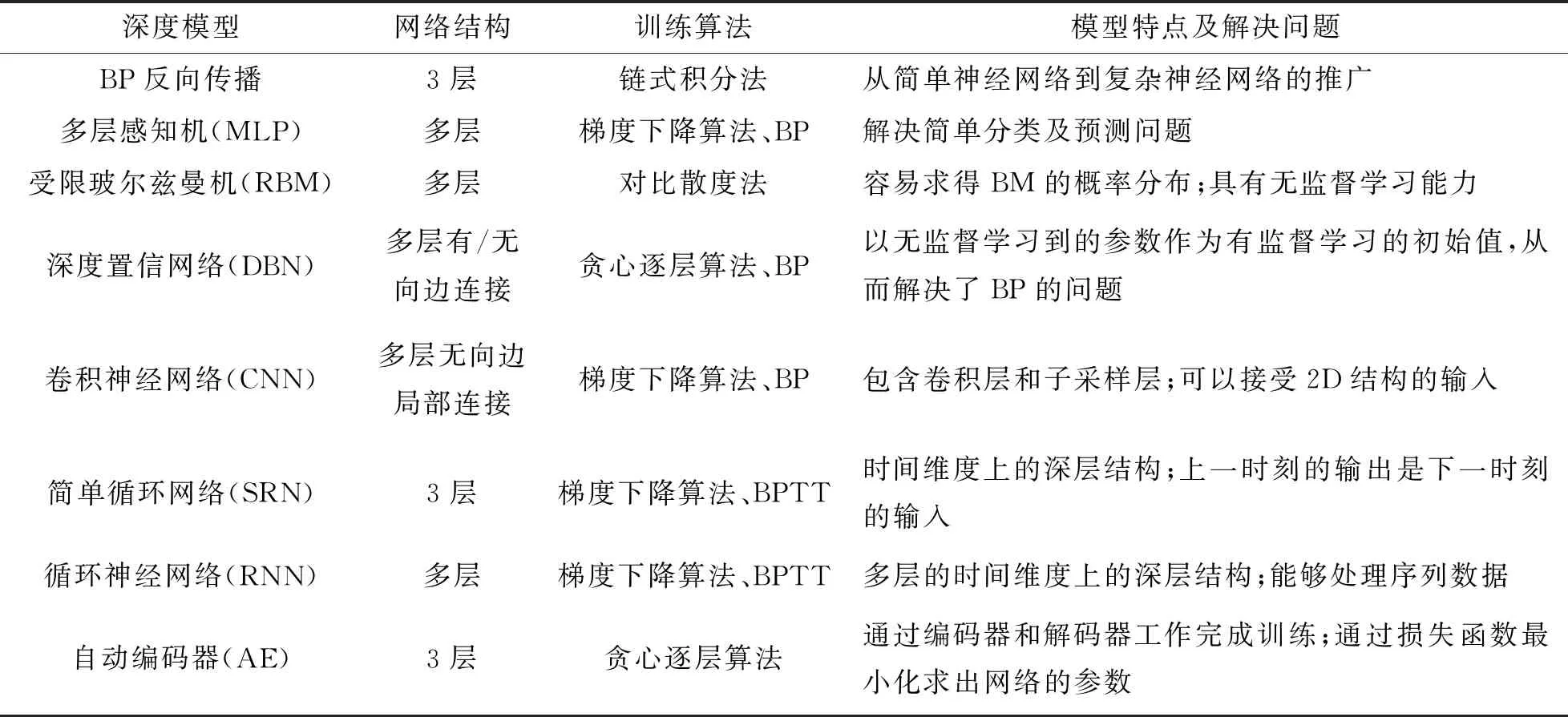
表1 深度学习常见模型及特点

模型预测的主要原理为根据历史数据输入选择的模型中进行训练，得到一个规则，当输入新的数据时这个训练好的规则可以预测得到结果，基本原理见图2。

图2 深度学习神经网络预测基本原理

(2) MLP模型适应性

MLP是感知机的推广，克服了感知机不能对线性不可分数据进行识别的弱点，能够逼近任意复杂的非线性函数关系，具有很强的自适应、自学习及容错能力，适合进行非线性函数拟合，可用于解决简单分类及预测问题，目前已在区域物流需求、蛋白质变性温度、短时交通流、广告点击率等方面进行了预测研究，且取得了较好的效果，服务区合理规模与各影响因素之间为复杂的非线性关系，MLP通过误差反传能够发现各因素与规模之间的映射关系，故选取MLP进行服务区合理规模预测。

4 基于MLP的合理规模测算模型

(1) 模型结构及变量选取

该文选取包含一个输入层、一个隐含层和一个输出层的3层MLP模型，根据服务区合理规模影响因素分析选取因素之间相关性较弱的作为输入层变量，综合分析选取主线断面交通量、驶入率、高峰率、周转率、车型结构及消费行为中较为重要的同行人数、消费水平和消费需求8个因素作为MLP神经网络输入层变量，各变量及其量化值见表2。

表2 输入层变量及代表量化值

隐含层神经元个数的确定通常采用试凑法确定，通过建立多个除隐含层神经元数量不同，其余条件均相同的MLP神经网络，比较网络迭代次数和误差精度来确定隐含层神经元个数，该文最终确定隐含层神经元个数为8个。输出层神经元为1个，即服务区合理规模，采用用地面积(m2)表示。

故该文建立的MLP神经网络合理规模模型各层神经元节点分别为(8,8,1)。

(2) 样本数据预处理

为提高网络的通用性，采用归一化方法对原始样本数据进行预处理，见式(1)。

(1)

在完成MLP神经网络训练之后需进行逆变换，将输出数据转换为原来服务区样本的数据特征，逆变换见式(2)：

(2)

式中：Xi为样本服务区第i个变量原始数据输入值；Ximax为样本服务区第i个变量原始数据最大值；Ximin为样本服务区第i个变量原始数据最小值；Xi′为变换后的样本服务区第i个变量数据。

(3) 模型训练

(3)

(4)

(5)

逆向传播过程通过梯度下降法不断降低损失函数(输出值与样本值之间的误差)，取网络所有输出层节点的误差平方和作为损失函数，见式(6)：

(6)

式中：yi为归一化后样本服务区输出层i节点合理规模期望值，ai为样本服务区输出层i节点合理规模输出值。

优化目标为确定W(权值)和b(偏置)使得损失函数C(W,b)最小，即网络输出的值会越来越接近真实值。W和b的迭代公式如下：

(7)

(8)

式中：α为学习速率，取(0,1]。MLP模型的训练采用Matlab编程实现，模型预测效果优劣选用绝对相对误差(rerr)、平均绝对相对误差(arerr)和均等系数(EC)进行评价。

(9)

(10)

(11)

式中：yk为服务区规模实际值；ak为服务区合理规模预测值；EC为均等系数，取值范围为(0,1)，表示服务区合理规模预测值与实际值之间的拟合度，EC值越大预测效果越好；EC值大于0.85，预测结果较好；EC值大于0.9，预测结果理想。

5 实例分析

运用2017年8月贵州省高速公路服务区实地调查数据进行分析。采用流量调查和问卷调查获取基础数据及出行者对服务区现有规模的满意度，以单个服务区(双侧)为对象，采用Spss进行数据处理、统计分析得到各服务区输入变量值及规模满意度，选取规模满意度大于80%的服务区作为样本服务区，最后选取贵州省乌江、久长等19个服务区作为样本服务区，输入变量及期望合理规模原始数据与归一化后数据见表3、4。

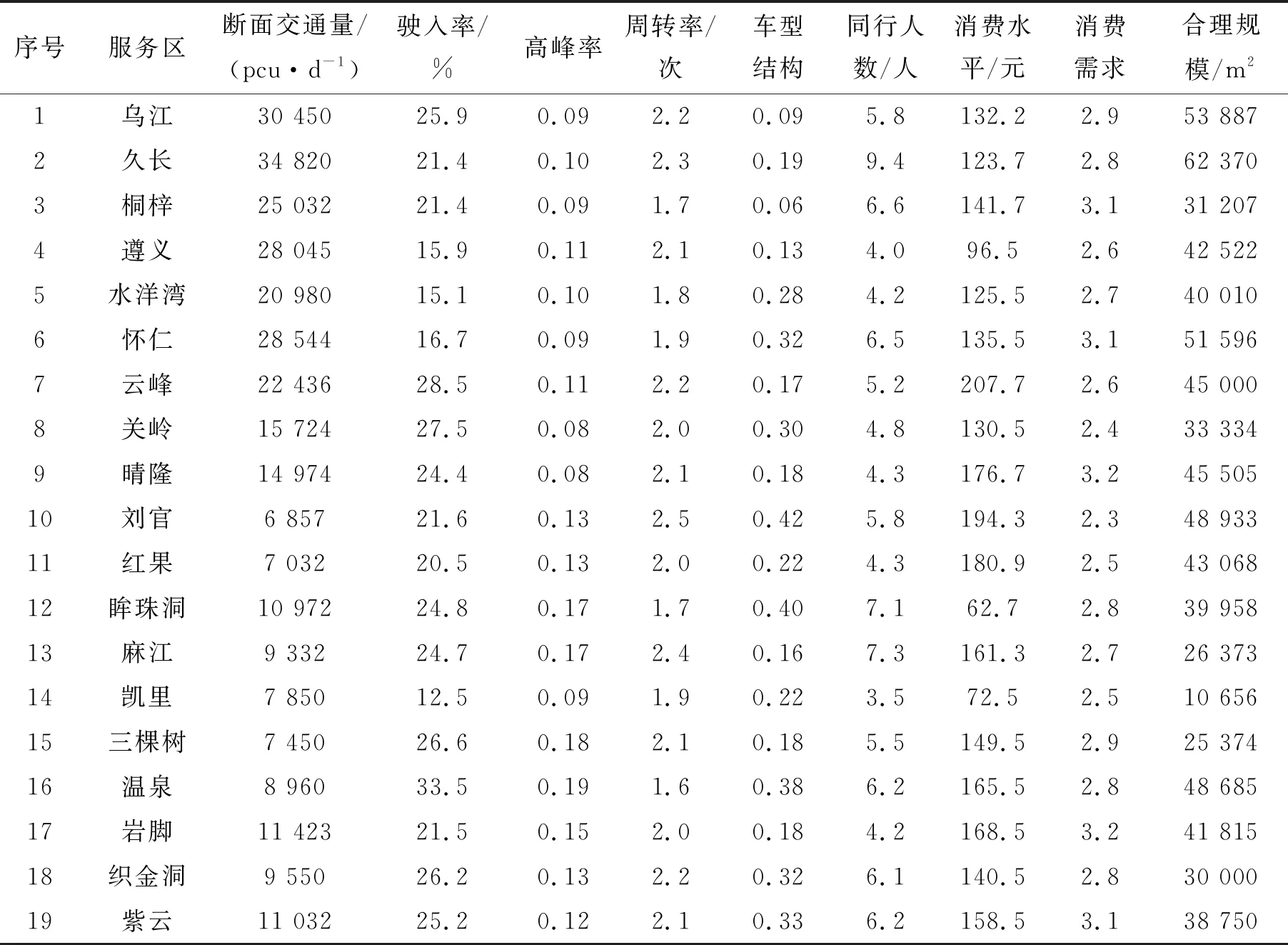
表3 样本服务区输入层及期望合理规模原始数据

表4 归一化后的样本服务区输入层及期望合理规模数据

抽取前15组数据作为训练样本，其余4组作为测试样本，MLP神经网络期望目标值设为0.01，学习速率为0.001，最大迭代次数为1 000，采用Matlab编程实现该搭建好的神经网络的训练，通过调试参数使网络达到训练精度要求，训练拟合曲线见图3，训练形成稳定的网络预测模型后，将测试样本进行仿真检验，得到仿真拟合曲线见图4，将测试输出结果反归一化后即为服务区合理规模预测值，并计算得到模型预测效果评价参数，见表5。

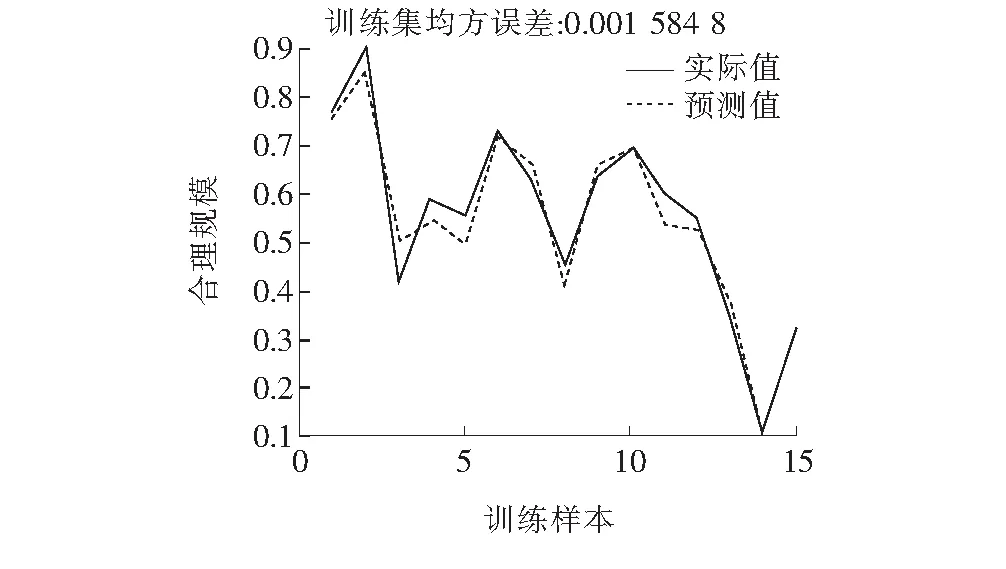
图3 训练集训练拟合曲线

图4 测试集仿真拟合曲线

表5 测试样本服务区合理规模测算结果及评价

由表5预测结果可知：4对服务区合理规模预测结果的绝对相对误差、最大绝对相对误差、平均绝对相对误差均在5%以内，均等系数为0.984 5，大于0.9，表明该合理规模期望值与预测值拟合度较高，预测结果理想，从而验证了所构建的基于MLP的合理规模测算模型的准确性和可行性。

6 结语

该文在分析高速公路服务区规模测算现有方法的基础上，结合高速公路服务区转型升级新要求，在研究服务区合理规模影响因素时充分考虑出行者消费行为及其他交通参数，构建基于MLP的合理规模测算模型，并用实际数据进行模型验证，结果表明该训练模型预测精度达到98%，可靠性较高，为服务区规划设计及升级改造提供了参考依据。该文所提出的合理规模测算模型亦可应用到其他方面的预测。