钢箱梁自行车桥的活荷载取值研究

2020-12-11叶代成

中外公路 2020年5期

叶代成

(厦门市市政建设开发总公司，福建厦门 361009)

“绿色交通”是实现可持续发展交通最强有力的手段之一，近年来国内外许多城市为解决由于城市交通问题引起的环境恶化，建设享有独立行驶路权的自行车道以推动实现“绿色交通”。阿姆斯特丹和哥本哈根等国外城市为合理利用土地资源，提高自行车通行效率和安全性，采取自行车高架桥的模式发展自行车交通。桥梁的结构设计又非常复杂，且活荷载在空间上和时间上具有极大随机性，中国已有一些学者对常规桥梁活荷载展开研究，如马虎迎等(2015年)开发了一种工字梁桥的活荷载剪力分布系数方程，并通过有限元现场测试评估验证该方程更利于桥梁设计；王赞芝等(2011年)通过计算抗弯惯矩修正系数和抗扭惯矩修正系数，探讨常见变截面连续箱梁桥活荷载内力增大系数计算方法；齐宏学等(2015年)以某三塔斜拉-自锚式悬索组合体系桥梁为背景，基于该桥梁结构特点选择合理的活载计算方法，通过非线性分析，研究活载作用下结构的受力情况。尽管关于桥梁活荷载研究成果较多，但未见涉及自行车桥活荷载取值的相关报道。与常规公路桥相比，自行车高架桥的活荷载比较小，荷载形式也比较单一，主要为自行车荷载。但由于自行车桥长度更长、桥面更薄、刚度更低，在自行车活荷载作用下的响应特征会有其自身特点，同时自行车桥活荷载的取值亦应与其结构特征相匹配，而不是仅考虑荷载本身的大小。因此，应针对自行车桥梁结构及自行车荷载的特点，确定与自行车高架桥自身结构特征相匹配的自行车活荷载取值。目前自行车高架桥在中国尚处于探索尝试的起步阶段，无专门的技术标准，只能参考JTG D60-2015《公路桥涵设计通用规范》和JTG B01-2014《公路工程设计标准》中的相关规定。

基于此，该文以中国首条钢箱梁自行车桥为案例背景，考虑自行车车道数量、骑行速度以及多车道荷载作用下不同车道荷载之间的相位差等因素，通过数值分析方法对各因素引起自行车桥梁结构挠度、内力和支座反力进行比较分析，根据分析结果研究钢箱梁自行车活荷载的取值建议，供结构设计和修订现行荷载规范参考。

1 自行车桥的活荷载取值影响因素

自行车桥的活荷载较小，主要为自行车荷载，其对自行车桥面板不是一个满布的均布荷载，而是通过车轮轮压作用于自行车桥面板上的局部荷载，并且该荷载的大小和作用位置对自行车桥面板某个区域而言是随时间变化的。影响自行车桥活荷载取值的因素包括自行车数量、设计车道数量、骑行速度和不同车道的自行车荷载错位加载，其中自行车数量及设计车道的数量是主要影响因素。骑行速度会引起桥梁的受迫振动，但自行车重量和骑行速度相对较小，不会引起自行车同桥梁的共振效应，因此骑行速度的影响相对较小。不同自行车车道荷载可能发生错开加载的情况，错开加载将引起不同的车道荷载之间出现相位差，从而导致移动荷载随时间变化与对齐加载的方式存在差别。

2 工程背景

为了解自行车及车道数量和骑行速度等因素对自行车桥结构的影响规律，现选取厦门市自行车桥作为研究对象。该项目位于厦门岛东部云顶路段，全线桥段共80联，为独墩连续梁体系。下部桥墩采用钢管混凝土，上部采用流线形钢箱梁作为主体受力结构，钢箱梁宽2.8 m，高1 m。钢箱梁主要由顶板、底板、腹板组成，具体构造见图1，钢材材质为Q345。

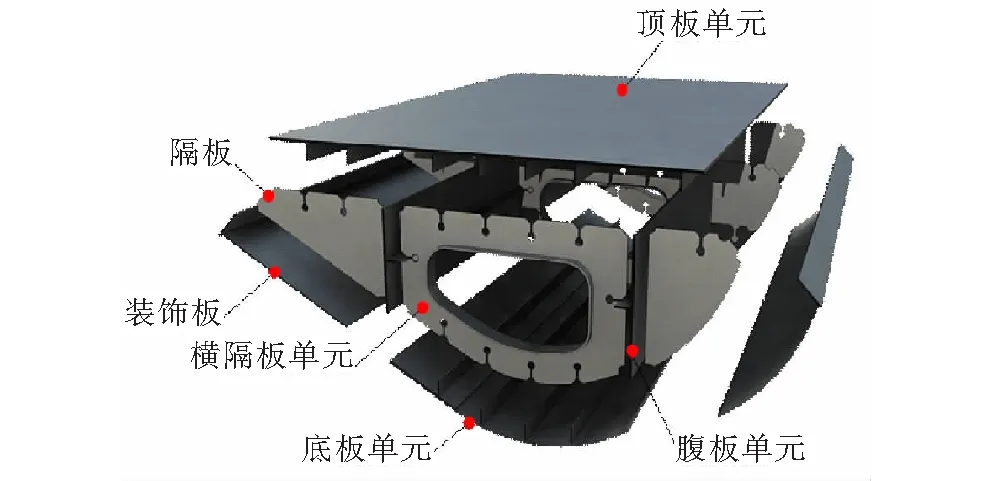
图1 钢箱梁结构图

3 数值模型设计

为研究桥梁挠度、内力和支座反力受力情况，借助有限元分析程序SAP2000进行影响面分析，以获取第1节所提的各个因素对桥梁结构的影响程度。限于篇幅，选取自行车桥第21联进行计算，该联包含分离曲线段、曲线分叉段和单幅曲线段等较多曲线桥跨。

3.1 材料参数

数值模型中，钢箱梁和桥墩结构均采用杆单元模拟，主要使用的材料和物理参数见表 1，参数包括：重度γ、密度ρ、弹性模量E、剪切模量G、泊松比υ、线膨胀系数α。

3.2 几何模型

选定的自行车桥第21联中包含有直线段和曲线段，共计6跨，总长41 m，如图2所示。为保证整个截面的面积等效和抗弯惯性矩等效，借助SAP2000截面设计器定义桥跨横截面，并根据自行车桥断面适当简化，横截面如图3所示。

表1 有限元模型中所使用材料物理参数

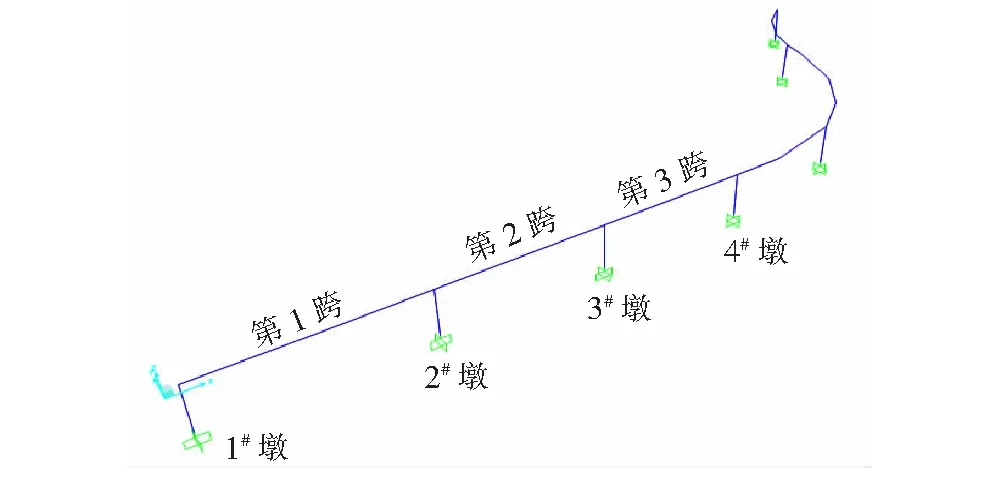
图2 自行车桥第21联(6跨)几何布置图

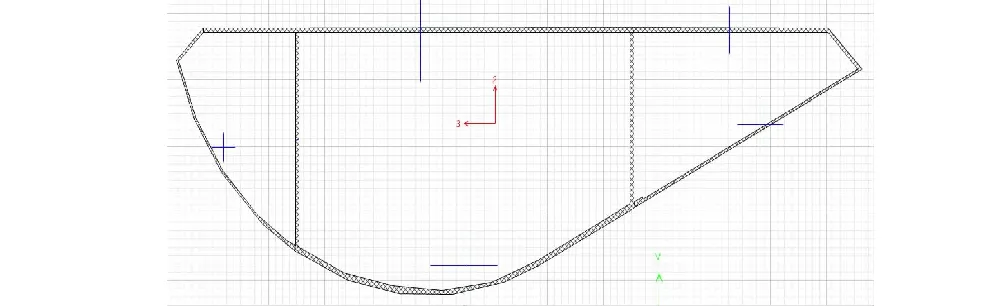
图3 截面示意图

3.3 计算工况

为充分考虑自行车桥在移动过程中对相邻跨内力的影响，根据该项目的跨度特点，以每2.7 m布置1辆2 kN自行车的车道荷载作为桥面活荷载的主要来源。为涵盖不同跨径满跨布载的情况，模拟自行车桥前轮与后轮集中力为1 kN，自行车长2 m，自行车与自行车之间的间距为2.7 m，总长为41 m。基于此，重点分析车道数量、骑行速度和多车道荷载错位加载情况的不同引起桥梁变形和内力的变化，共考虑24种计算荷载工况，如表2所示。

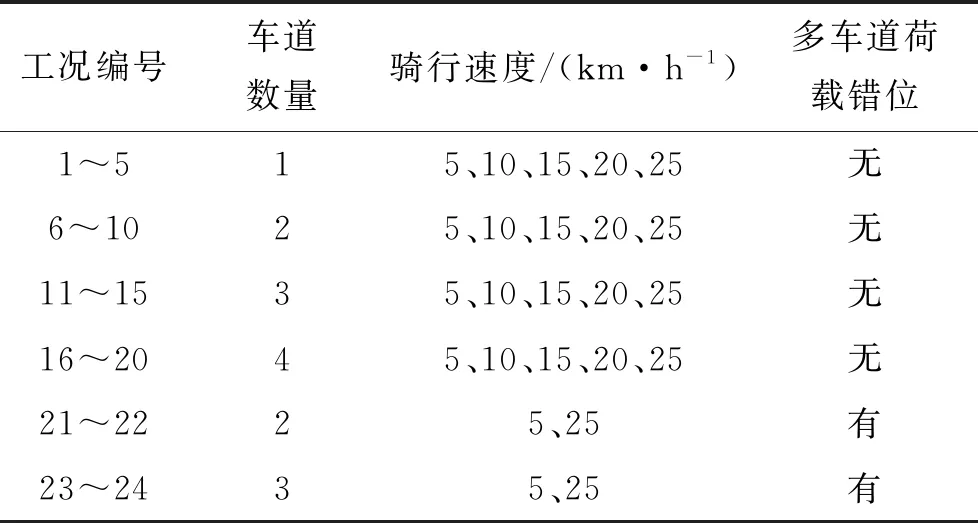
表2 计算工况

4 计算结果分析

4.1 不同车道数量和骑行速度对桥梁挠度的影响

单列自行车不同骑行速度下(第200荷载子步)桥梁的挠度变化如图4所示。

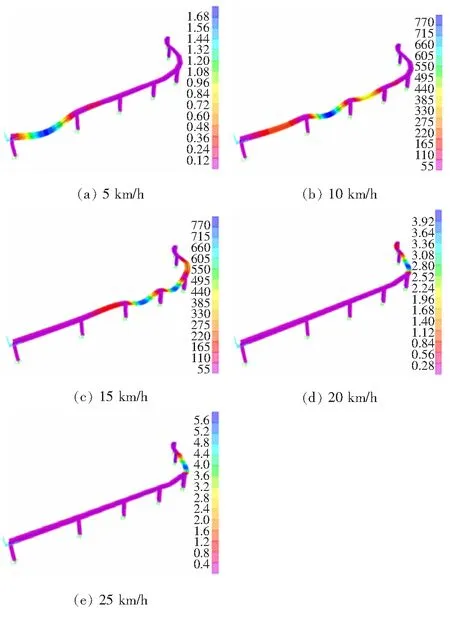
图4 单列自行车不同骑行速度下桥梁挠度变形(单位：mm)

从图4可以看出:速度为5 km/h时第200子步荷载作用在第1跨，最大挠度为1.68 mm；速度为10 km/h时第200子步荷载作用在第2跨和第3跨之间，最大挠度为0.77 mm；速度为15 km/h时第200子步荷载作用在第3跨和第4跨之间，最大挠度为0.77 mm；速度为20 km/h时第200子步荷载作用在第5跨，最大挠度为3.92 mm；速度为25 km/h时第200子步荷载作用在第5跨，最大挠度为5.6 mm。由上可知，在跨度相近时，弯桥段的变形最大，也反映出弯桥抗弯刚度较直桥段小。

15 km/h移动荷载作用不同自行车道数量下(第200荷载子步)桥梁挠度变形情况和最大挠度值分别见图5和表3。

从图5可以看出:无论单列自行车荷载作用在横断面中心线上的情况，还是多列自行车荷载根据中心线进行偏心加载的情况，桥梁的挠度仍然随车道数量保持高度的线性变化。结合表3可知:不同自行车道荷载作用下桥梁结构的挠度有所不同，由于桥梁采取钢箱梁截面，其抗扭刚度较大，因此不同车道设置对自行车桥的挠度成线性比例发展，未受到因自行车车道偏离桥梁中心线而导致扭转变形进而引起挠度发生非线性的增长。

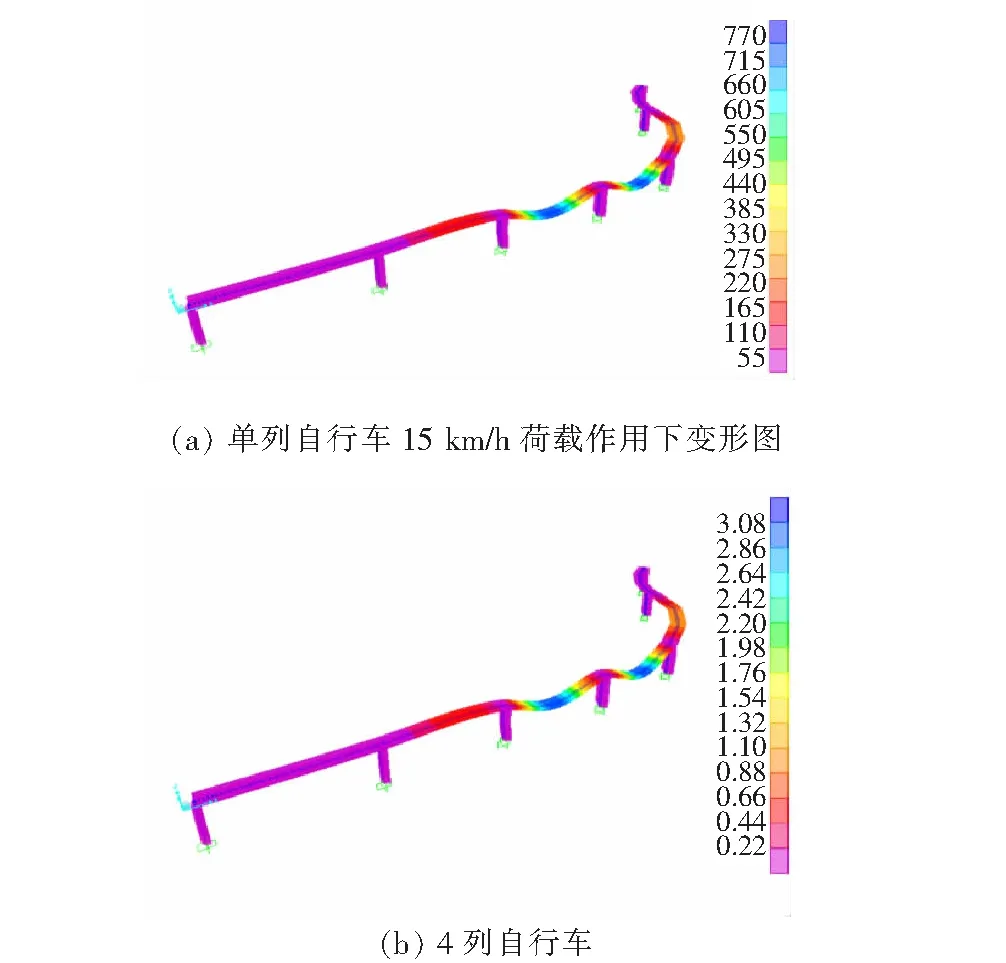
图5 15 km/h移动荷载作用不同自行车道数量下桥梁的挠度变形图(单位：mm)

表3 15 km/h移动荷载作用不同自行车道数量下桥梁的最大挠度

4.2 不同车道数量和骑行速度对桥梁内力的影响

桥梁结构的内力是考察自行车荷载响应的重要指标之一，现选取第3跨跨中作为内力取样点，分析第3跨跨中内力在不同的车道数量以及不同的车速作用下的变化规律。

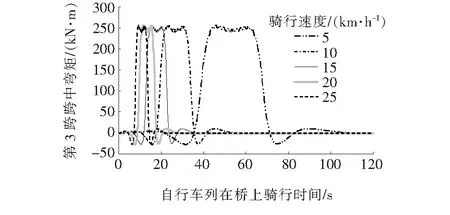
单列自行车不同骑行速度荷载作用下第3跨跨中弯矩随时间的变化曲线如图6所示。

由图6可知:不同的骑行速度跨中弯矩最大值是一致的，保持在84.5 kN·m左右，骑行速度仅影响最大弯矩的到达时刻。其中5 km/h到达时刻最晚，发生在第45.2 s，其他骑行速度时从10～25 km/h对应的最大弯矩到达时刻依次提早，最大值最早发生在第8.8 s。

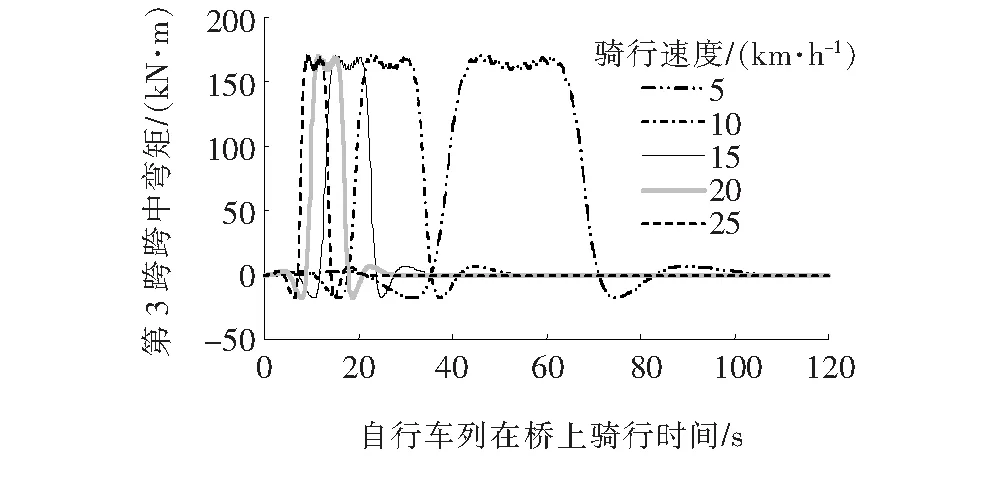
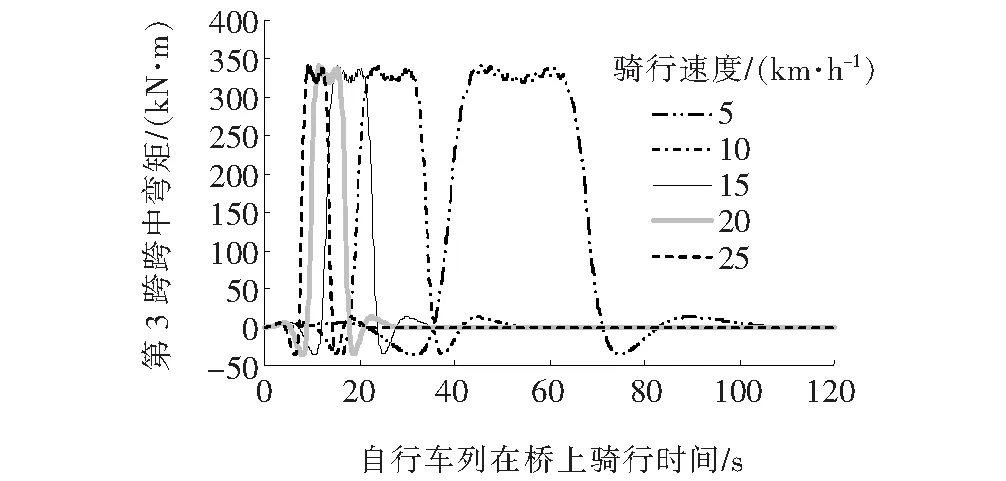
2～4列自行车车道移动荷载下的弯矩变化规律如图7所示。

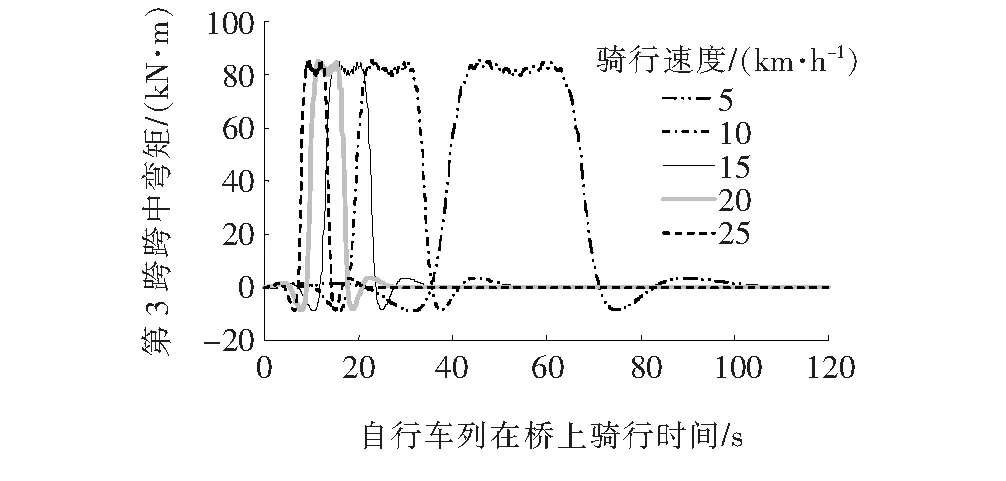
图6 单列自行车不同速度作用下第3跨跨中弯矩图

(a) 2列自行车

(b) 3列自行车

从图7可以看出:多车道的弯矩变化规律同单车道的情况基本相同。弯矩极值基本不受骑行速度的影响，骑行速度仅影响最大弯矩的到达时间；另一方面，不同的第3跨跨中弯矩最大值同自行车车道数量呈现出明显线性关系，从单车道的85 kN·m到双车道的169 kN·m以及3车道的256 kN·m和4车道的341 kN·m，最大弯矩值同车道数量保持线性增长的关系。由此可见,桥梁的刚度较大，尤其是抗扭刚度较大，自行车的偏心效应在荷载弯矩响应方面表现不明显，最大弯矩始终同自行车车道数量呈线性关系。

为了更为明显地对比第3跨跨中弯矩同自行车车道的对应关系，图8给出了25 km/h骑行速度对应1～4车道第3跨跨中弯矩随加载时间的变化。

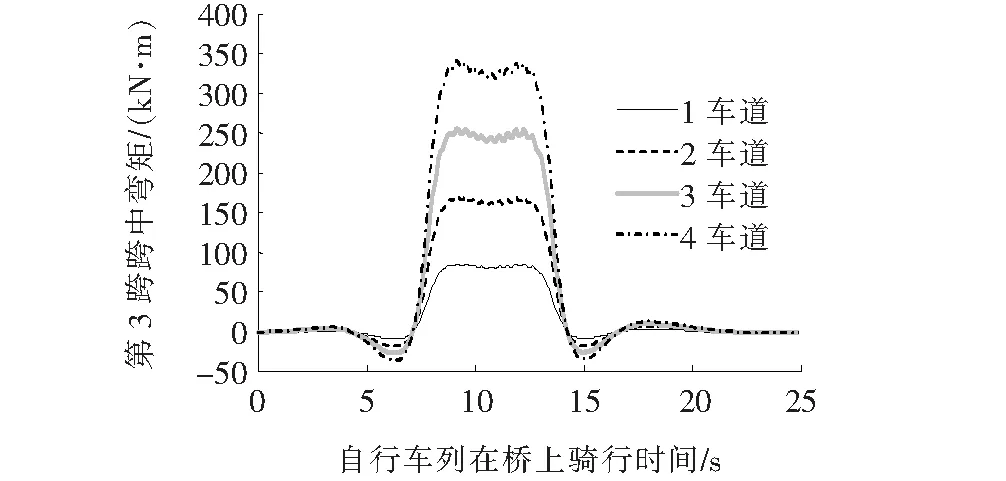
图8 25 km/h骑行速度下第3跨跨中弯矩随车道数量的变化曲线

由图8可知:单车道和多车道的曲线变化趋势保持高度的一致性。此外，第3跨跨中弯矩的大小同车道数量按照线性的比例增加，可以发现弯矩的大小未受车道偏心加载的影响，进而说明桥梁具有充分的抗扭刚度。

4.3 不同车道数量和骑行速度对桥梁支座的影响

支座反力作为衡量桥梁受力特点的另一个重要指标，现选取第4桥墩作为支座反力取样点，分析第4桥墩处支座反力在不同的车道荷载以及不同的车速作用下的变化规律。

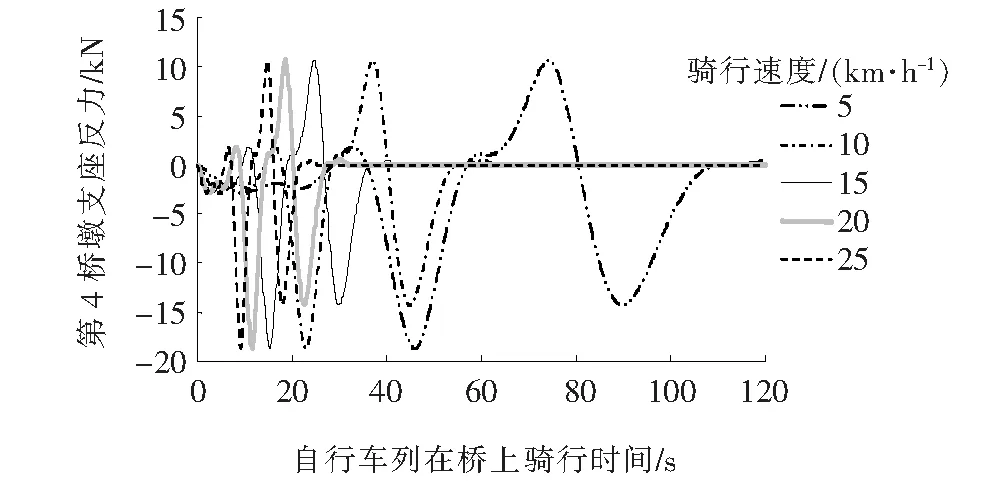
单列自行车不同骑行速度荷载作用下第4桥墩处支座反力随时间的变化曲线如图9(a)所示。

从图9(a)可以看出:不同的骑行速度下第4桥墩支座处支座反力最大值是基本相同的，最大值为10.56 kN左右，骑行速度仅影响最大反力到达的时刻，其中5 km/h到达时刻最晚，发生在第74.2 s，其他的骑行速度时从10～25 km/h对应的到达时刻依次提早，最早发生在第14.8 s。双车道至4车道的自行车荷载作用下第4桥墩处支座反力的变化规律示于图9(b)～9(d)中。

(a) 单列自行车

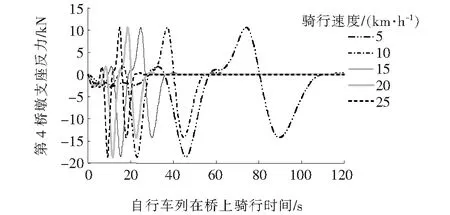
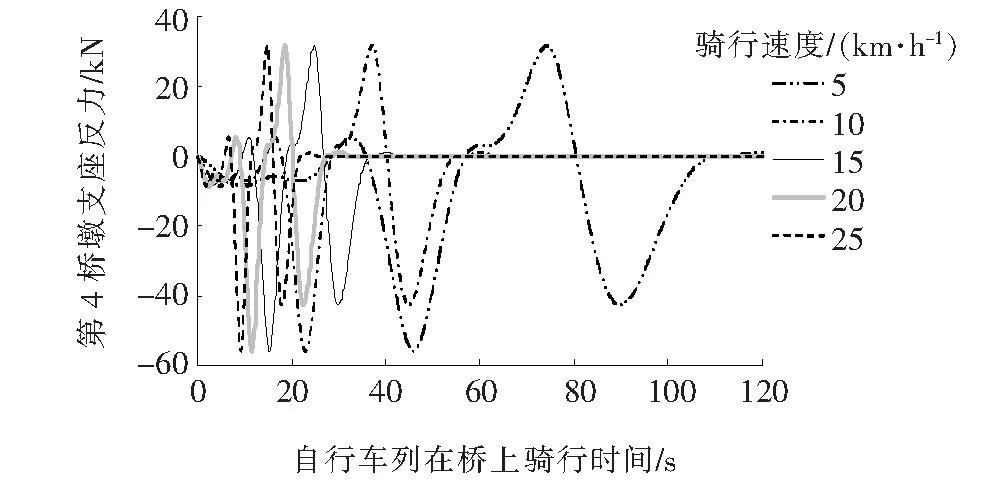
(b) 2列自行车

(d) 4列自行车图9 不同骑行速度下第4桥墩处支座反力图

由图9(b)～9(d)可知：多车道的弯矩变化规律同单车道的第4桥墩处支座反力变化规律基本相同，基本不受骑行速度的影响，骑行速度仅影响最大支座反力的到达时间。第4桥墩处支座反力最大值同自行车车道的数量呈现出明显的线性关系，从单车道的10.56 kN到双车道的21.12 kN以及3车道的31.7 kN和4车道的42.272 kN，最大支座反力值同车道数量保持线性增长的关系，同上节中跨中弯矩变化趋势相似。

为对比第4桥墩处支座反力同自行车车道的对应关系，图10给出了骑行速度为25 km/h时对应的1～4车道第4桥墩处支座反力随加载时间的变化曲线。

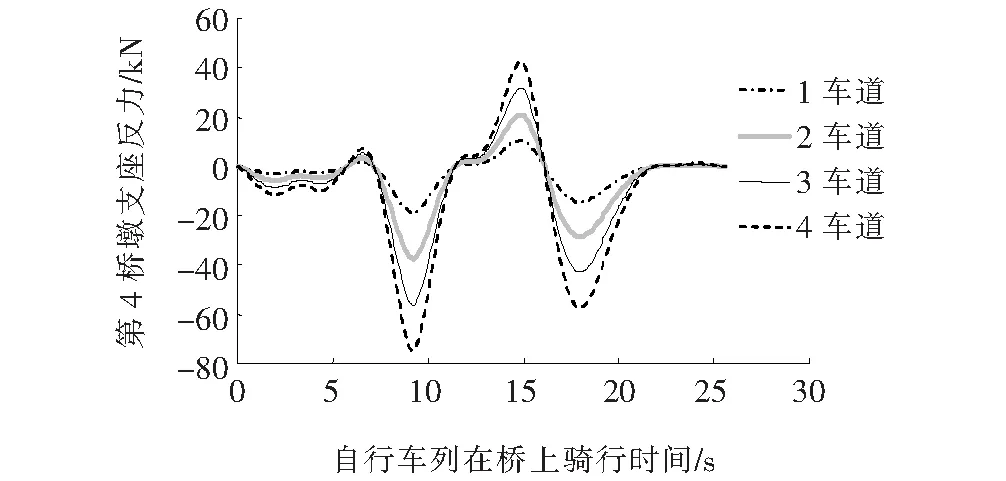
图10 25 km/h骑行速度下第4桥墩处支座反力随车道数量变化曲线

从图10可以看出：单车道和多车道的曲线变化趋势保持高度的一致性，第4桥墩处支座反力的大小同车道数量呈线性比例增加。

4.4 多车道荷载错位对桥梁内力的影响

为精确研究错位加载差别对桥梁内力的影响，通过在多车道自行车车列荷载作用下分别施加对齐加载和不同车道错位加载两种不同形式的荷载，研究荷载错位导致的弯矩最大值的变化。现仍选取第3跨跨中弯矩作为研究对象，分别提取双车道和3车道在对齐加载和错位加载情况下，桥梁跨中弯矩随时间的变化曲线。

5、25 km/h速度作用下双车道荷载对齐(无错位)及错位加载的第3跨跨中弯矩和加载时间对比曲线分别如图11、12所示。

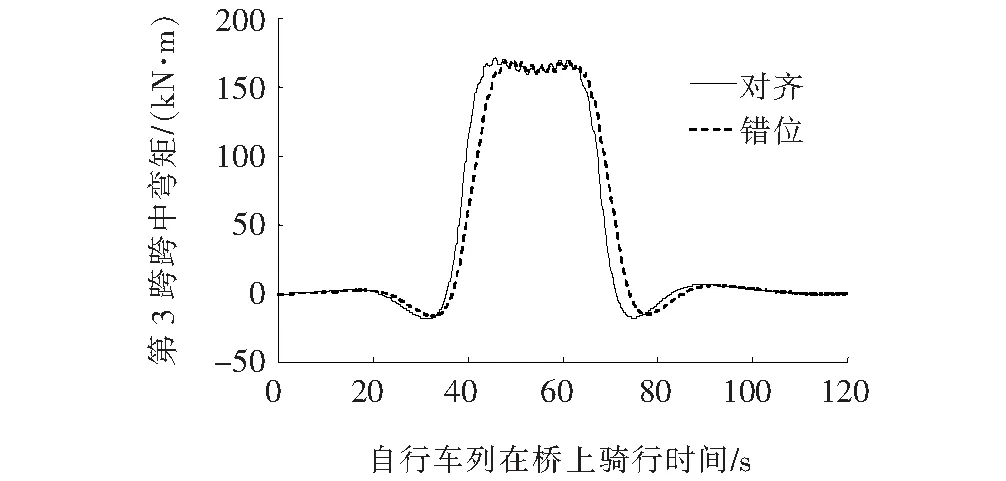
图11 双车道5 km/h骑行速度下第3跨跨中弯矩图

从图11可以看出：无错位加载的情况弯矩最大值率先出现，较错位加载情况提前3 s，两者曲线的变化趋势基本一致，此时间差是车道之间荷载所错位距离和当前速度的比值。荷载从最小值变化到最大的区间内弯矩差别越来越大，当对齐荷载跨中弯矩达到最大值时，差别值达到最大，之后一直呈减小的趋势，卸载过程同加载的过程相反；从图12可以看出：25 km/h的曲线变化趋势同5 km/h的曲线基本一致，但是由于骑行速度变大，两者之间的时间差变小，最大弯矩持续时间也比5 km/h有很大的减小，所持续的时间为5 km/h的20%左右。由图11可知：车道荷载对齐工况下第3跨跨中最大弯矩为170.4 kN·m，错位加载工况为168.8 kN·m，两者差别在2%以内。图12中车道荷载对齐工况下第3跨跨中最大弯矩为170.6 kN·m，错位加载工况为168.7 kN·m，两者差别也在2%以内。

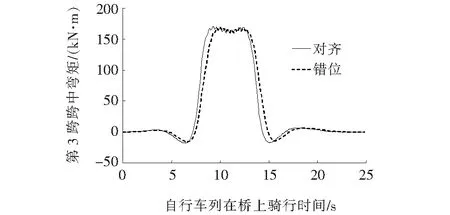
图12 双车道25 km/h骑行速度下第3跨跨中弯矩图

5、25 km/h速度作用下3车道荷载对齐及错位加载的第3跨跨中弯矩和加载时间对比曲线分别如图13、14所示。

图13 3车道5 km/h骑行速度下第3跨跨中弯矩图

图14 3车道25 km/h骑行速度下第3跨跨中弯矩图

从图13、14可以看出：3车道5、25 km/h速度作用下弯矩曲线的变化规律同图11、12基本一致。不同的是，5 km/h速度作用下对齐工况对应的第3跨跨中最大弯矩为257.0 kN·m，错位加载时为250.2 kN·m，两者差别在3%以内；25 km/h速度作用下对齐工况对应第3跨跨中最大弯矩为255.9 kN·m，错位加载时为246.4 kN·m，两者差别也在3%以内。

4.5 最大骑行速度下不同车道数量的内力包络结果分析

3列自行车道以25 km/h速度骑行时对应的桥梁整体弯矩包络结果如图15所示。

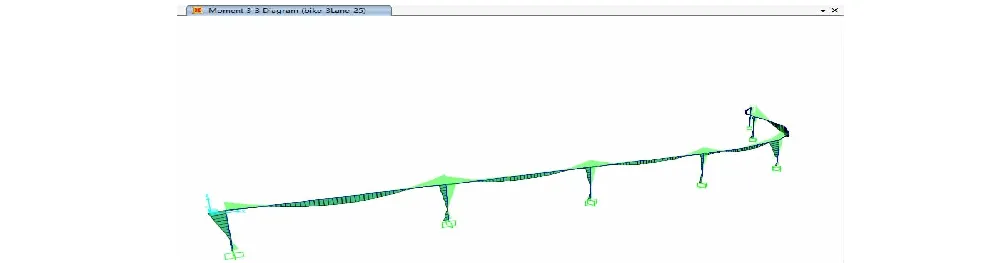
图15 3列车道25 km/h移动荷载作用下桥梁整体弯矩包络图

从图15可看出：3列自行车道以25 km/h速度骑行时对应的桥梁全断面主弯矩包络结果，直接反映了内力的变化规律和趋势。其中深色阴影为最大正弯矩，浅色阴影为最大负弯矩，最不利内力出现位置以及对应的极值，均可作为设计桥梁活荷载标准值的重要参考。然而传统的影响线计算方法一次仅能够得到单元断面内力，无法一次性获取所有截面的最不利响应。因此，借助有限元强大的计算能力，通过穷举法能够对复杂桥梁进行准确且精细的分析，不仅能够获取整个桥跨不同截面位置处桥梁内力最大和最小包络结果，以作为活荷载设计的重要参考；还能有效地判断不同形式荷载发生最不利内力响应的位置，以作为精细化计算活荷载的有效补充。