曲线钢箱梁平转体施工悬臂状态有限元分析

杨柳， 张清， 王阳建， 陈得良*

(1.长沙理工大学 土木工程学院，湖南 长沙 410114; 2.深圳市路桥建设集团有限公司)

桥梁转体施工几乎不会对要跨越的既有工程造成任何交通影响，同时又能加快施工进度，所以当需要跨越交通繁忙的道路或水路时会被广泛应用。转体施工分为平转法、竖转法和平竖转结合法，平转法应用最多。平转法是指在桥墩(台)设置转盘，利用牵引系统将上部结构由非设计轴线位置平转到设计轴线位置的一种施工方法。目前转体施工桥梁大多为直桥和大半径弯桥梁，对于受现场条件限制而采用的小半径钢箱梁桥中国国内研究较少，难点在于曲线效应会带来横桥向大偏心，对施工过程中保持转动体系的平衡挑战很大。其次，钢箱梁作为空间薄壁结构，在弯扭耦合作用下，应力分布情况要比一般桥梁更为复杂，因此对大曲率钢箱梁转体施工进行受力仿真分析十分必要。

1 工程概况

该转体施工(50+80+50) m连续钢箱梁位于广(州)深(圳)沿江高速公路深圳段二期工程SJ1合同段H匝道桥第5联。工程横跨广深高速公路，采用先节段拼装后墩底平面转体施工(图1)。为了避免不对称施工，单个桥墩上部转体梁长均设为(39+39) m。施工方法为搭设临时支架，14#、15#桥墩临时固结，节段拼装至设计转体梁长，分步进行转体施工后，调整线形，再进行边跨、中跨段合龙

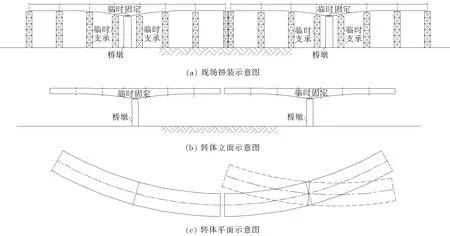
图1 钢箱梁现场拼装和转体示意图

。

箱梁平面位于R=150 m曲线段上，桥面横坡为6%，钢箱梁顶宽10.5 m，底宽6.5 m，梁体高2.5～4.5 m。钢箱梁主要由正交异性板和各自的加劲肋组成，顶底板厚度分为16、24、30 mm3种，腹板厚度分为14、20 mm2种，顶、底、腹板纵肋厚度分别为10、12和11 mm，钢箱梁每2 m设一道14 mm厚的纵向横隔板，支座附近横隔板加密。

2 有限元模型

针对钢箱梁转体部分(39+39) m的主体结构，采用Ansys壳单元Shell63对其进行对称建模。该桥在转体前完成了桥面护栏施工，剩余桥面系及附属工程是在边、中跨合龙后再施工，因此还需对防撞护栏部分采用质量单元Mass21进行模拟，得到单个桥墩上部钢箱梁转体总重量为738.7 t。转体施工中支座临时固结，支座中心点位于x=1 m和x=2.5 m处。对支座处面域进行固定约束，整个模型处于悬臂状态，其中x轴指向曲线外侧。

3 最大悬臂状态下受力和变形分析

3.1 偏心距计算

钢箱梁纵桥向平衡，由于钢箱梁曲率大，存在较大的横桥向偏心。转体施工中需通过设置预偏心和配重来平衡原本的偏心，使结构重心与转动体系的中心尽量重合。该文用Ansys软件计算得钢箱梁的理论重心向其轴线内侧横向偏心1.573 2 m，施工图设计的横向预偏心为桥墩中心线偏离钢箱梁轴线1 m，而桥墩中心线又与转动体系的中心线偏离0.3 m，整个结构对于转动体系中心线的偏心距计算示意图如图2所示。

图2中：G1为钢箱梁自重，G2为桥墩自重，N为转体总重量，e1为钢箱梁自重与转动体系中心的偏心距，e2为桥墩与转动中心的偏心距，可得整体对于转动体系的偏心距为：

在计算整体偏心距时，对于钢箱梁的有限元模型则需考虑平弯曲率的影响以及各个构件的几何尺寸、材料等。此外，因为是墩底转体施工，桥墩偏离转动中心，因此计算整体的偏心距必须考虑桥墩的自重。

该文所计算的整体偏心距较小，配置之前若偏心距小于15 cm，可以不考虑配重，由此表明施工图所设计的预偏心比较合理，无需配重。

图2 转体施工偏心距计算示意图(单位：m)

3.2 挠度变形分析

图3为钢箱梁在最大悬臂状态下的位移变形云图。从图3可以看出：钢箱梁在最大悬臂状态下的挠度最大值出现在钢箱梁顶板曲线内侧，其大小为9.27 cm。

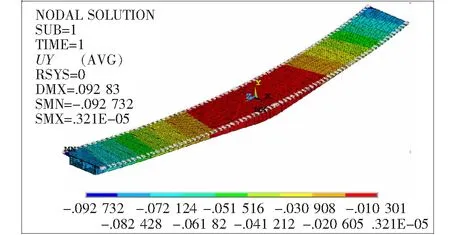
图3 (39+39) m钢箱梁静力分析总位移云图(单位：m)

图4为钢箱梁顶板曲线内侧和外侧的挠度变化图。图4表明：对于大曲率钢箱梁，在最大悬臂状态下，其曲线内侧变形挠度要大于曲线外侧的变形挠度，二者变形相差接近1 cm。表明平弯钢箱梁在弯扭效应作用下，其在悬臂状态下的内、外侧变形是不同的，且内侧挠度要大于外侧变形挠度。这种变形差异值需在钢箱梁合龙段以及线形控制、制造过程中引起重视，否则将导致合龙和线形误差以及次生应力。

3.3 应力分析

3.3.1 整体应力分析

图5为最大悬臂状态下钢箱梁的第一主应力云图。图5表明：在最大悬臂状态下，钢箱梁在墩顶两边各L/2(L=39 m)内，其顶板、悬臂板和腹板上缘出现了较大的主拉应力，该主拉应力区间为[18.3，41.2] MPa，其最大主拉应力值41.2 MPa位于曲线内侧L/4附近的顶板。

图4 钢箱梁顶板曲线内外侧挠度变化图

图5 (39+39) m钢箱梁第一主应力云图(单位：Pa)

以曲线外侧为正向，选取横桥向距离主梁轴线1.5、3.0、4.5 m以及轴线处的7组顶板节点进行分析，图6为这7组顶板节点主拉应力沿桥梁纵向的变化关系。图6表明：主拉应力的最大值并没有出现在墩顶位置，而是在距墩顶12 m附近出现，这与变截面、变厚度、临时约束以及横隔板的分布等有关。同时图6还反映出距墩顶一定距离内(约L/4)，顶板都有较大主拉应力，该区域内墩顶处顶板主拉应力最大，而在L/4外的位置主拉应力则随距离的增大而减小。表明变截面悬臂钢箱在施工过程中最大悬臂状态的应力监测不能只关注墩顶位置。

图7为最大悬臂状态下钢箱梁的压应力云图。图7表明：钢箱梁在最大悬臂状态下，出现较大主压应力的位置是：在墩顶两边各L/2内的底板和腹板下缘，该主压应力区间为[-38.1，-85.7] MPa，最大压应力出现在墩顶附近。

图6 顶板纵桥向主拉应力变化图

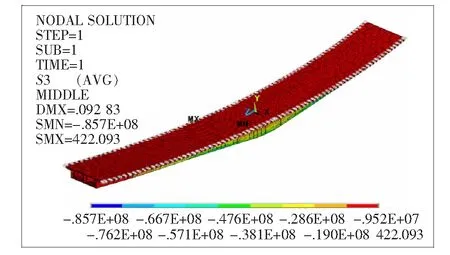
图7 (39+39) m钢箱梁第三主应力云图(单位：Pa)

图8为底板主压应力沿桥梁纵向的变化关系。其5组节点分别为距主梁轴线1.50 m、轴线处以及曲线内外两侧的5组节点。图8表明：底板主压应力的峰值同样出现在z轴12 m附近，其他与主拉应力变化趋势类似。所不同的是，x=1.5 m以及曲线内侧的底板因在墩顶位于支座固结区域而压应力骤减至0，存在突变。

图8 底板纵桥向主压应力变化图

3.3.2 截面应力分析

图9、10分别为墩顶附近横截面(z=0.5 m)的主拉应力和主压应力云图。图9表明：对于墩顶横截面，其主拉应力在顶板位置最大，而在底板处最小；图10则表明：主压应力在顶板处最小，而在底板处最大，且随横截面高度变化规律明显，其中底板压应力为0的区域为支座固结区域。

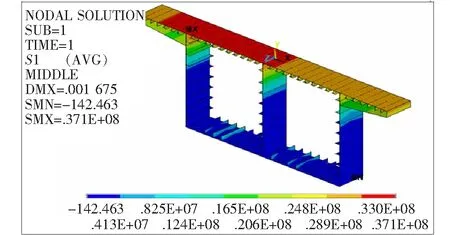
图9 墩顶横截面主拉应力云图(单位：Pa)

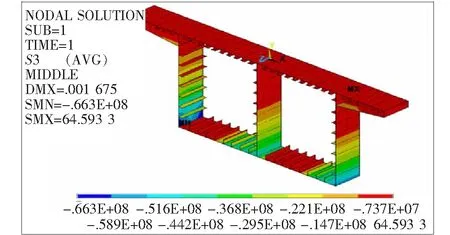
图10 墩顶横截面主压应力云图(单位：Pa)

表1为钢箱梁最大悬臂状态下各个关键横截面主拉应力和主压应力峰值的分布情况。

图11为不同截面处顶板主拉应力随横桥向的变化规律。图11表明：钢箱梁在曲线内外两侧顶板悬臂部分与腹板交接处(x=3.25 m)、顶板与中腹板交接处(x=0)均存在横桥向主拉应力突变，其余位置顶板主拉应力变化相差不大。

图12为不同截面处内侧腹板应力随高度的变化关系，正值表示主拉应力，负值表示主压应力。图12表明：悬臂端截面腹板的应力接近0，其他截面腹板的应力向上、下两端逐渐增大，在与顶板相接处达到拉应力最大值，与底板相接处达到压应力最大值。

3.3.3 曲率变化对偏心、挠度以及应力的影响

为了研究曲率变化对转体施工的影响，依次讨论曲线半径为50、60、70、75、80、150、200、300、600、800和1 000 m的11组其他尺寸相同的钢箱梁，得到了横向偏心以及最大下挠值的变化规律，如图13所示。图14为钢箱梁最大主拉应力和最大主压应力随曲率的变化规律。

表1 钢箱梁最大悬臂状态下关键横截面应力分布

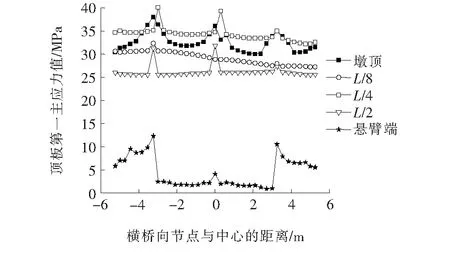
图11 顶板横桥向主拉应力变化图

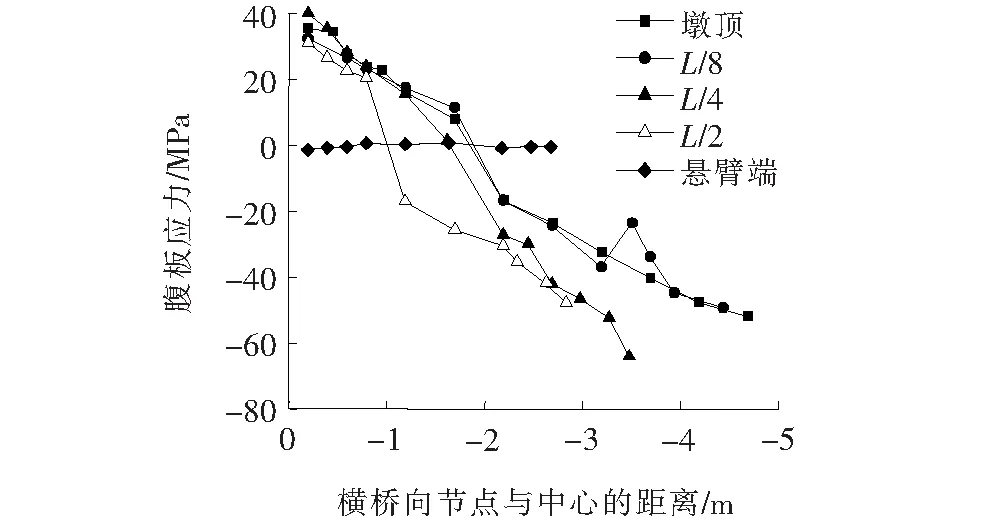
图12 腹板应力随高度的变化图

图13 横向偏心以及最大挠度随曲率变化图

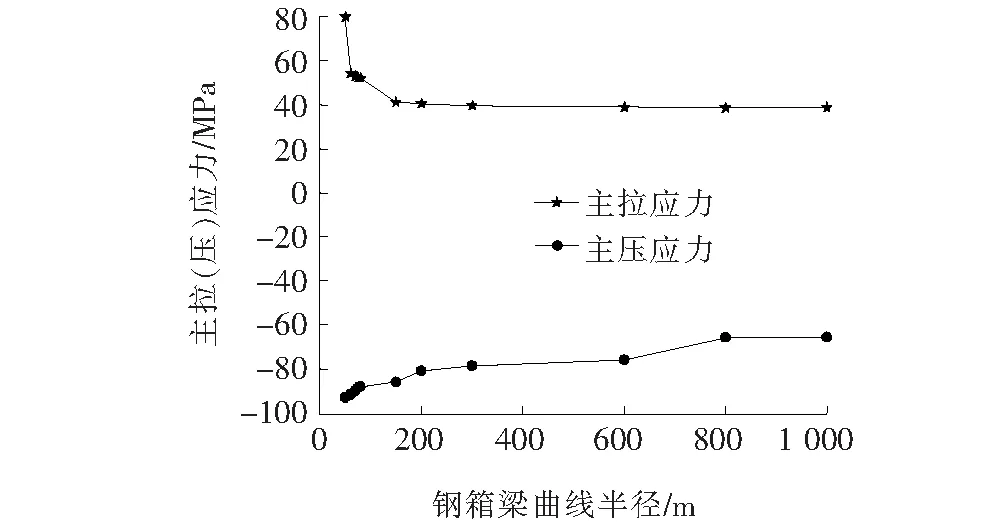
图14 钢箱梁最大主拉、压应力随曲率变化图

图13、14表明：当曲线半径超过800 m时，弯桥会逐渐趋于直桥，此时曲率的影响可以忽略，而当曲线半径小于300 m时，曲线半径越小，钢箱梁的横向偏心、变形以及应力就越大，曲率对转体施工影响也就越大，尤其当曲线半径小于70 m时，横向偏心会大于1/2底板宽3.25 m，此时很难设置较大的预偏心，只能通过横向配重来保证转体施工平衡。因此，合理的曲线半径和底板宽是十分必要的。

4 结论

通过对深中通道深圳侧接线H匝道桥第5联钢箱梁在最大悬臂状态下的受力和变形进行有限元分析，得到如下结论：

(1) 平弯钢箱梁在曲线内侧存在较大的横向偏心，可采用设计预偏心的方法进行纠偏。

(2) 平弯钢箱梁在弯扭耦合效应作用下，在最大悬臂状态下内、外侧挠度变形是不同的，这种变形差异值需在钢箱梁合龙段以及线形控制和制造过程中引起重视。

(3) 钢箱梁最大悬臂状态应力分布合理，但在纵桥向距中心1.5 m处的曲线内侧腹板下缘出现较大的压应力，应考虑增大墩顶附近腹板刚度。

(4) 应力分布规律研究表明：钢箱梁弯扭耦合效应明显，最大应力不只存在于墩顶位置，为保证转体施工过程中的安全，应重点在墩顶两边各L/4内，监控顶板和底板，横截面重点监控各个腹板的上下缘与顶、底板的交接处。

(5) 钢箱梁曲线半径超过800 m时，曲率的影响可以忽略，当曲线半径小于300 m时，曲线半径越小，横向偏心、变形及应力越大，转体施工挑战越大。曲线钢箱梁转体施工设计底板尺寸时应考虑横桥向偏心的影响。