基于随机响应面法的基坑地连墙可靠度分析
2020-12-11郯俊彬邵国建
郯俊彬, 邵国建, 余 杰, 郦 纲, 楼 伟, 孙 阳
(1.河海大学力学与材料学院,南京 210000; 2.杭州京杭运河二通道建设投资有限公司,杭州 310003;3.河海大学港口海岸与近海工程学院,南京 210000)
随着城市化进程的加快,地面空间的开发利用趋于饱和,地下工程数量逐年增加,深基坑施工也越来越普遍. 基坑开挖深度越深,地质条件越复杂,施工难度越大,施工风险也会增大[1-2]. 基坑工程中,支护结构的水平位移是评价基坑稳定安全的重要指标之一,许多基坑事故都是因为支护结构水平位移超限而破坏,因此利用可靠度理论评价基坑支护结构的稳定性是基坑工程中一项重要课题.
基坑工程是一项复杂的岩土工程,由于土体参数、土层厚度以及施工荷载等均是基坑工程中常见的不确定性因素,它们均具有随机性和变异性,安全系数法受到限制,可靠度理论充分考虑了参数的不确定性,被应用到基坑支护结构可靠度研究中. 近年来,许多学者对基坑支护结构可靠度进行了大量的研究[3-4]. 黄广龙等[5]利用可靠度分析方法评价了基坑围护结构的整体稳定性,发现采用可靠度指标评价基坑稳定性较安全系数更加合理,并且分析了参数变异性对结果的影响. 朱鸿鹄等[6]基于现场实测数据,结合贝叶斯修正和Monte Carlo有限元法评估了基坑开挖过程的安全可靠度. 廖瑛等[7]采用响应面法对基坑支护结构进行了可靠度分析,并与一次二阶矩法作对比,发现响应面法计算简单,收敛速度快,计算精度也能保证,还研究了土体参数对结构可靠指标的影响.
近年发展较快的随机响应面法也被许多学者应用到各类结构可靠度分析中[8-14],如胡冉等[15]基于随机响应面法对结构进行可靠度分析. 李典庆[16]等将渗流有限元计算与随机响应面法相结合,对心墙堆石坝渗透稳定性进行了可靠度分析. 王卿和黄淑萍[17]将随机响应面法应用于单桩沉降的可靠性分析,盛建龙和翟明洋[18]采用随机响应面法对岩质边坡进行了可靠度分析,并对比了四种抽样配点方法对响应面拟合精度和可靠度分析结果的影响. 目前,随机响应面法较少应用于支护结构可靠度研究,本文结合ABAQUS 有限元软件和随机响应面法,对基坑支护结构进行可靠度分析,并且对比分析土体参数的随机性对随机响应面的拟合精度和可靠指标的影响,为基坑支护结构的可靠度研究提供参考.
1 随机响应面法
1.1 基本原理
随机响应面方法输入变量为随机数,由标准随机变量建立结构的响应面方程,采用抽样配点方法结合有限元方法得到响应面表达式中的待定系数. 随机响应面方法由于计算效率和计算精度较高,且收敛性在数学意义上得到保证,对于功能函数无法用显示表达式描述的复杂结构的可靠度分析,它是一种十分有效可行的方法.
1998年,Isukapalli 等[19]最早提出随机响应面法理论,并将其应用于研究环境和生物系统的不确定性问题. 随机响应面法可以将有限元法和不确定分析法结合起来,解决了实际工程中极限状态方程难以用显式函数表示的问题,且相较于标准蒙特卡洛法计算量大大降低. 随机响应面法主要步骤如下:将结构的随机变量表示为标准随机变量,随机响应面采用Hermite随机多项式表达,采用概率配点法求出多项式中的待定系数,得到拟合的极限状态方程,结合蒙特卡洛法求解结构可靠度. 结构的随机变量X 表示为标准正态分布随机变量U 的函数:

式中:X 为随机变量,U 为标准正态分布随机变量,F-1()为X 累积概率分布函数的反函数,Φ()为标准正态分布的累积概率分布函数. 若随机变量X 服从正态分布,则它和标准正态分布随机变量U 的映射关系为:

其中:μx和σx为随机变量X的均值和标准差. 随机响应面的Hermite随机多项式为:

其中:a0、ai1、ai1i2等为待定系数;n 为标准正态随机变量的数目;Γn(Ui1,Ui2,…,Uin)为n 阶Hermite多项式.
1.2 抽样配点方法

拉丁超立方抽样(LHS)是一种从多元参数分布中近似随机抽样的方法. 在确定抽样配点数目N 后,将[0,1]区间等分成N 个互不重叠等概率区间,然后利用逆变换法在各个子区间上抽取一个样本,最终得到所需的N 个配点.
2 基坑工程实例
2.1 工程概况
马銮北站为地下二层岛式站台车站,单柱双跨框架结构,全长347.602 m,标准段基坑宽度20.7 m,深度约为14 m,大里程端深度约为11 m,顶板覆土约3 m. 小里程端为异形基坑,深度约为14 m. 车站主体围护结构采用地连墙+内支撑体系,地连墙厚度为600 mm,基坑施工时共采用2道内支撑,标准段第一道支撑为混凝土支撑,间距8~9 m,第二道为钢支撑,间距2~3 m,小里程端两道支撑均为混凝土支撑,间距3~4 m. 基坑中间设置临时立柱,临时立柱桩基础采用∅1000 mm的灌注桩. 基坑底板主要位于凝灰熔岩残积黏性土层,地连墙墙趾进入全风化凝灰熔岩层. 车站周边无重要建筑物,均为当地村民鱼塘,场地开阔,周边影响范围内无管线,施工条件较好. 马銮北站总平面图如图1所示.
基坑工程沿线地层结构较复杂,岩土层分布不均,工程地质条件差,岩土层的埋深、厚度及性能变化较大. 素填土层具有均匀性差、自重压密性及低强度、高压缩性等不良工程特性,不利于边坡稳定. 软土为海积淤泥,流塑~软塑状,具有压缩性高、强度低、灵敏度高、透水性低等不良工程特性,对工程有一定的影响.砂混淤泥以次圆状石英质中、粗砂为主,含泥质约30%. 分选较差,工程性能不良. 残积土和全、强风化岩均匀性较差,强度不一,遇水易软化,强度急剧降低,工程性能总体不良.
该基坑工程的地质条件较为特殊,根据谭宏大等[20]对于凝灰熔岩残积土的试验研究可知,该土体抗剪强度随含水率增大而减小,当初始含水率较小时,抗剪强度的变化速率较大. 因此,为确保支护结构的稳定性,必须对支护结构进行可靠度分析. 岩土体的主要物理力学参数见表1.

表1 岩土物理力学指标Tab.1 Physical and mechanical indexes of rock and soil
2.2 基坑有限元模型
基坑开挖过程中不考虑地下水的影响,选取标准段典型断面进行有限元数值模拟. 建立基坑模型,模型的侧面边界到地下连续墙的距离分别取为基坑宽度的3 倍,在深度方向上从基坑底部向下取为基坑开挖深度的3倍. 为简化计算,基坑岩土体共分为5层,土体本构选择摩尔-库伦弹塑性本构模型,基坑网格划分如图2所示.
有限元模型计算中,岩土体单元、地连墙和混凝土支撑均为C3D8R 实体单元,钢支撑为B31 梁单元. 假定地连墙与土体之间接触面摩擦系数为0.3,基坑两侧10 m 范围内添加均布荷载10 kPa. 边界条件:计算模型侧面受到X 轴和Z 轴方向的水平位移约束,约束模型底面,限制X、Y、Z三个方向的变形.
利用ABAQUS 有限元软件对基坑开挖过程进行数值模拟,采用生死单元功能实现基坑开挖. 经过计算,得到基坑开挖完成后支护结构的侧向变形情况.由图3可知,基坑开挖至基底后,支护结构整体变形呈现为“弯弓”状,最大侧向位移为22.48 mm,最大侧移处距离地表约为9.5 m.

图2 基坑网格划分Fig.2 Mesh generation of foundation pit

图3 地连墙侧向位移Fig.3 Lateral displacements of diaphragm wall
3 支护结构可靠度分析
3.1 可靠度计算
由于基坑工程中支护结构的侧向位移是评价基坑稳定性的重要指标之一,也是基坑安全可靠的最重要指标之一. 基于支护结构变形控制设计理论,依据支护结构的最大侧向位移建立支护结构的功能函数,以土体参数作为随机变量进行可靠度分析.
由于第四、五层土体绝大部分均位于地下连续墙下面,基坑开挖对于地连墙的扰动较小,故仅考虑上面三层土体的随机性和变异性对支护结构侧向变形的影响. 为了分析各类土体参数对于结构可靠度的影响,将三层土体的弹性模量E(E1、E2、E3)、内摩擦角Φ(Φ1、Φ2、Φ3)和黏聚力C(C1、C2、C3)作为三组随机变量进行支护结构可靠度分析. 假定所有随机变量均服从正态分布且相互独立,变异系数均取为0.1. 地连墙侧向位移是关于随机变量的隐式函数,故以支护结构最大侧向位移建立极限状态方程:

式中:X1、X2、X3为随机变量;fmax为支护结构的最大侧向位移控制值;f 为支护结构的最大侧向位移计算值. 该基坑工程根据《城市轨道交通工程监测技术规范》,支护结构最大侧移应当不超过30 mm.
采用随机响应面方法建立基坑支护结构的随机响应面函数,随机响应面函数即为式(4)中的f,为了满足计算精度要求,一般采用3阶Hermite随机多项式来表示. 将服从正态分布的基本随机变量转化为标准正态分布随机变量,分别采用概率配点法和拉丁超立方抽样方法选取40 个配点,然后将这40 个配点代入ABAQUS有限元软件计算得到支护结构最大侧移计算值,将40个配点和对应的最大侧移计算值输入随机响应面法程序,得到响应面函数表达式,结合蒙特卡洛模拟方法求得基坑支护结构的失效概率和可靠指标.
由于支护结构侧向位移没有显式函数且该问题没有蒙特卡洛近似精确解,所以在可靠度分析之前须对随机响应面函数的拟合精度进行验算,以保证结果的准确性. 采用相关指数R2描述随机响应面函数在整个空间上对真实功能函数的拟合精度. 相关指数R2介于0和1之间,越接近1表示随机响应面函数拟合精度越高. 相关指数的计算公式如下:

式中:n 为实测样本点数目(配点数目);yi、yi∗分别为第i 个样本点对应的实测值和随机响应面函数值(拟合值);为实测均值.
随机变量分别为E、Φ和C 的拟合精度结 果 如 图4、5、6 所示. 由图可知,三种随机变量的随机响应面函数拟合精度都很高,相关指数R2均超过0.99,其中随机变量为弹性模量时,随机响应面的拟合精度最高,随机变量为内摩擦角和黏聚力时,随机响应面的拟合精度稍差一些.

图4 随机变量为E的拟合精度Fig.4 Fitting accuracies of random variable E

图5 随机变量为Φ的拟合精度Fig.5 Fitting accuracies of random variable Φ
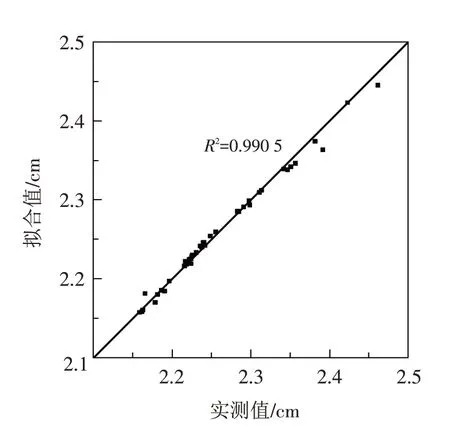
图6 随机变量为C的拟合精度Fig.6 Fitting accuracies of random variable C
3.2 可靠度计算结果对比分析
结合ABAQUS有限元软件和随机响应面法,得到支护结构的随机响应面函数,经过拟合精度验算,证明了基于概率配点法的随机响应面法是准确的. 此时,支护结构的功能函数已知,结合蒙特卡洛方法,进行100万次蒙特卡洛模拟得到支护结构的失效概率和可靠指标. 图7展示了三种随机变量计算得到的可靠指标.
由图7可知,当支护结构侧向位移控制值逐渐减小时,三种随机变量模式下支护结构的可靠指标均越来越小,且当控制值小于29 mm时,可靠指标与控制值近似为线性关系. 随机变量为土体弹性模量时,可靠指标随着控制值的减小降低幅度最大,而随机变量为土体内摩擦角和黏聚力时,可靠指标随控制值的变化较为一致,且均比随机变量为弹性模量时可靠指标高. 这表明在变异系数相同情况下,土体弹性模量的随机性和变异性对于狭长基坑支护结构的稳定性影响更大,在评价基坑支护结构稳定性时,应当首先关注土体弹性模量的随机性. 此外,Wang[21]等针对工程小概率问题,推荐了结构的目标可靠指标,可靠指标大于3.0 表明工程预期性能高于平均水平;可靠指标大于4.0 表明预期性能水平较高;可靠指标大于5.0表明预期性能很高. 该基坑工程的支护结构最大侧向位移控制值设定为30 mm,三种随机变量情况下结构可靠指标均大于4.5,说明基坑设计和施工满足变形控制要求,基坑稳定性较好.

图7 支护结构的可靠指标Fig.7 Reliable indexes of supporting structure
4 结论
基于ABAQUS有限元软件和随机响应面法,结合蒙特卡洛模拟,计算了基坑支护结构的可靠指标,并分析不同土体参数作为随机变量对拟合精度和可靠指标的影响,结论如下:
1)基于概率配点的随机响应面法可以应用于基坑地连墙的可靠度分析中,三种随机变量情况下,相关指数R2均超过0.99,表明拟合精度很高;
2)三种随机变量情况下,弹性模量对结构可靠指标的影响明显,可靠指标随着控制值的减小降幅较大,内摩擦角和黏聚力对可靠指标的影响稍小,可靠指标随着控制值的变化较为一致;
3)当地连墙的最大侧向位移控制值为30 mm时,三种随机变量下支护结构的可靠指标均超过4.5,表明基坑稳定性较好.
