连续介质渗流区域非线性问题数值求解分析
2020-12-11潘广良
潘广良
(方正县河湖运行保障中心,黑龙江 方正 150800)
0 前 言
土石坝的非线性渗流求解在于渗流自由面和溢出面的确定。文章基于移动网格法、单元渗透矩阵调整法和复合单元高斯点法,运用Microsoft Developer Studio可视化集成开发二维无压渗流分析有限元程序,结合具体算例求解连续介质渗流区域的非线性问题,成果对渗流区域非线性问题研究具有重要意义。
1 绪 论
中国目前的岩土体水力学研究,为实际应用和方便处理考虑,基本选用线性数学模型。线性数学模型通常将渗流运动和物体状态简化处理,因此助推岩土体水力学近些年快速发展[1]。但实际渗流由多种因素复合影响而成,绝大多数的渗流分析均呈非线性,故材料的非线性问题在岩土体水力学研究中为基本问题,具有十分重要的研究价值。
2 渗流基本原理和数学模型
连续介质渗流区域非线性问题以二维非稳定流的饱和渗流模型为例,4种表达方程式[2]如下:
1)Boussinesq方程:在自由面进行流量补给,并将缓变形式简化为水平向渗流,在区域地下水活动研究中应用广泛。
(1)
2)Laplace方程:自由面既可进行流量补给,同时为下降流速的限值条件,表达式为:
(2)
3)扩散方程:自由面不进行流量补给,该方程仅针对自由面微弱变化的均质土坝,表达式为:
(3)
4)固结方程:因考虑到土体具有压缩性,常应用于粘土筑坝的固结,表达式为:
(4)
3 算例分析
3.1 移动网格法
连续介质渗流的二维有限元模型分为2种不同单元进行划分,三角形单元和8节点四边形等参单元[3]。算例为一均质土坝,坝面宽6m,上、下游水位分别为4m和3m,计算模型示意图,见图1。
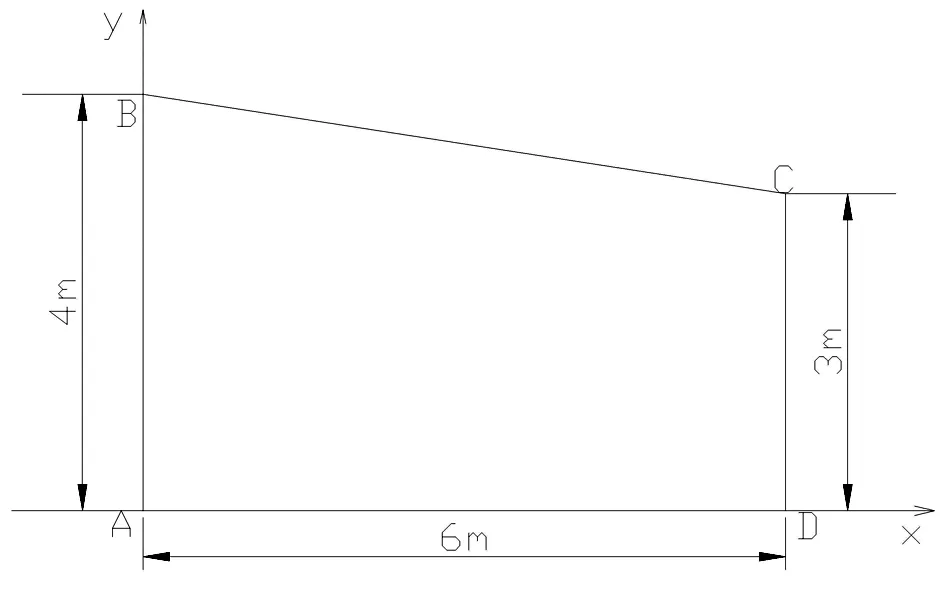
图1 计算模型示意图
边界条件:渗流边界BC无补给,AD为封闭边界。
模型进行三角形单元划分时,共划分18个单元,16个结点;八节点四边形单元划分时,共划分为9个单元,40个结点,三角形单元网格剖分,见图2;八结点四边形等参元网格剖分,见图3。
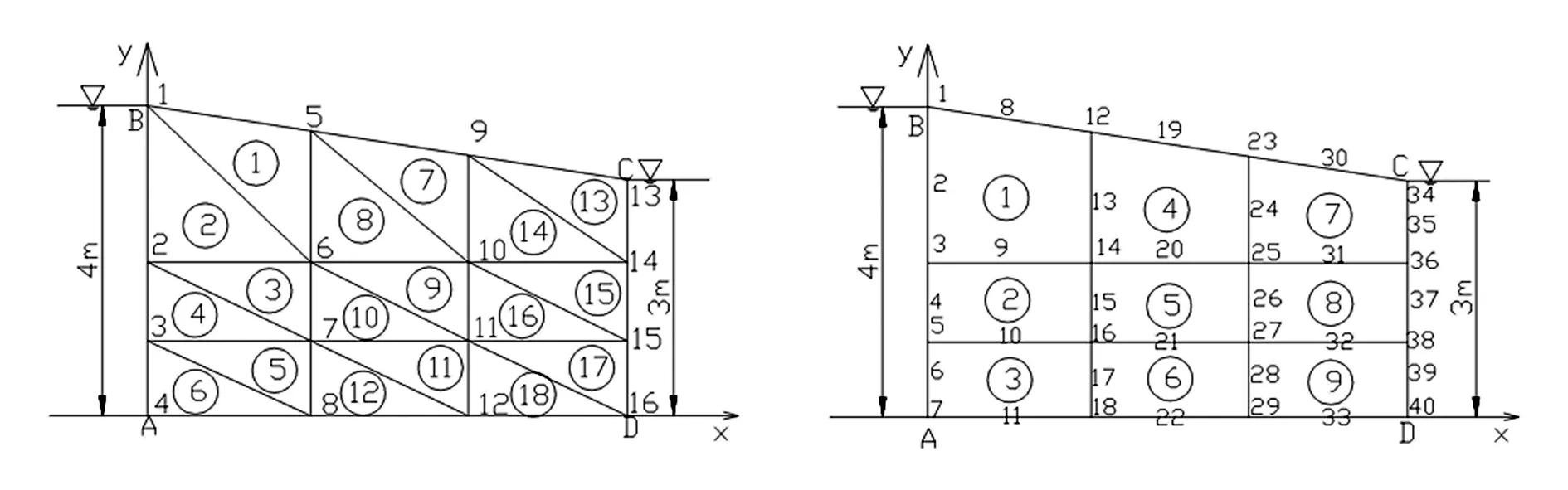
图2 三角形单元网格剖分 图3 八结点四边形等参元网格剖分
通过程序模拟计算,得到2不同单元的渗流自由面结点水头计算结果值,区域渗流自由面结点水头对比值,见表1。

表1 区域渗流自由面结点水头对比值
3.2 单元渗透矩阵调整法[4]
该法的无压渗流分析单元划分原理同基本网格法。算例为一均质土坝,高8m,宽4m,上、下游水位6.0m和1m,该均质土坝模型,见图4。

图4 均质土坝计算模型
边界条件:BC边界无流量补给,流量为零,CD边界流量可能溢出,AE为封闭边界。本算例先选用四边形单元剖分模型,共剖分24个单元,93个结点。四边形单元网格剖分,见图5。
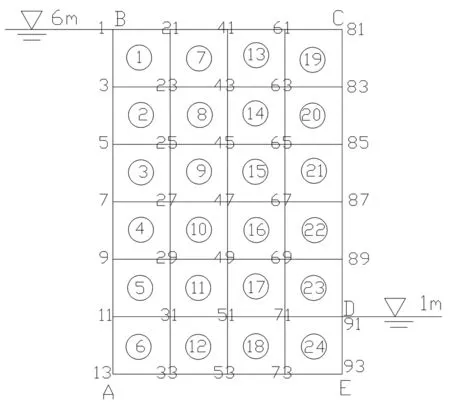
图5 四边形单元网格剖分
为保证迭代的稳定性和结果的精确性,进行5次迭代后计算得出溢出点水头值5.68m,渗流自由面各节点水头统计值,见表2。

表2 渗流自由面结点水头统计值
由结果可得,在相同节点不同数解值有较大差距数,故在四边形单元基础上再次进行三角形网格加密,共划分单元48个,结点35个,三角形单元网格剖分,见图6。
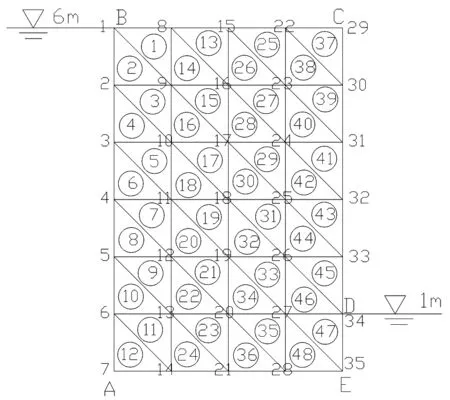
图6 三角形单元网格剖分
本次求解进行10次迭代后得到渗流面溢出点水头值为3.23m,模型的渗流自由面和节点水头结果见图7和图8,渗流自由面各节点水头统计值,见表3。

图7 计算模型渗流自由面

图8 节点水头等值线图

表3 渗流自由面结点水头统计值
由上述结果可得,网格加密的渗流求解更加贴合实际,为更好证明自编程序的合理性,重新运用四边形单元加密划分模型,本次单元划分单元150个,节点501个,模型单元划分结果见图9。迭代9次后得到自由面水头值为3.78m,计算模型渗流自由面,见图10;节点水头等值线图,见图11;渗流自由面结点水头值,见表4。

表4 渗流自由面结点水头值
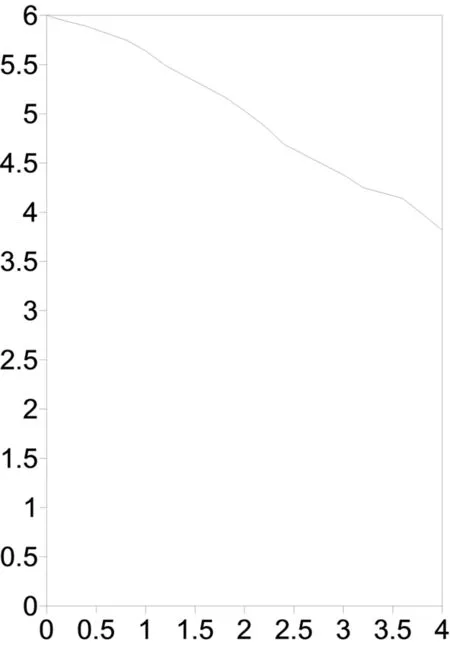
图10 计算模型渗流自由面

图11 节点水头等值线图

图9 模型四边形单元网格剖分
由表4可知,单元进行加密后的2解相差减少,对比上述方法的计算结果,本法更加吻合实际。
3.3 复核单元高斯点法[5]
对上算例进行复核单元高斯点法求解,得到计算结果如下:渗流自由面节点水头统计值见表5;对比不同方法的代表水头结果见表6,经迭代9次后得到自由面水头值为3.35m。不同方法得到的渗流自由面上典型点水头值及误差见,计算模型渗流自由面和节点水头计算值见图12和图13。

表5 渗流自由面结点水头值

表6 渗流自由面代表节点水头计算统计表

图12 计算模型渗流自由面

图13 节点水头等值线图
通过上述结果表明,复合单元高斯点求得的渗流面节点位置更贴合实际,误差仅为5.2%,远<单元渗透矩阵调整法,二者均能体现渗流区域震荡,在实际应用中均有自身的利用优势,但在同样的前提条件下,复合单元高斯点具有更适宜的合理性应用。
4 结 论
文章在连续介质渗流区域非线性问题求解的基本原理基础上,建立不同算例进行建模,采用3种不同方法有限元计算对应算例的渗流区非线性问题,得出不同模型的渗流自由面和代表节点水头值,认为在相同条件下,复合单元高斯点法更能贴合实际应用,同时验证了自编程序的合理性和准确性。
