基于有限元和极限平衡法的边坡稳定性分析
2020-12-11陈松
陈 松
(水利部新疆维吾尔自治区水利水电勘测设计研究,乌鲁木齐 830000)
0 引 言
近年来,在计算方法、软件设计、高速低成本硬件等方面都有了迅速的发展。与边坡稳定性分析特别相关的是极限平衡法和有限元法。然而,当使用极限平衡法分析边坡时,在确定临界滑动面(取决于地质情况)并由此确定安全系数时,可能会出现一些计算困难和数值不一致的情况。尽管存在这些固有的局限性,但由于其简单性,极限平衡仍然是最常用的方法。然而,随着计算机的普及,有限元法在边坡稳定性分析中的应用越来越广泛。与极限平衡相比,有限元的一个优点是不需要对临界破坏面的形状或位置进行假设。此外,该方法还可以方便地与其他方法一起用于计算路堤中的应力、位移、孔隙压力和渗流引起的破坏,以及监测渐进破坏[1-3]。董晓红对边坡的极限平衡和有限元分析进行了综合评述,将有限元分析结果与现场测量结果进行了比较,发现计算变形有大于测量变形的趋势[4]。邵龙潭使用极限平衡法和极限分析法对边坡进行了分析,发现这两种方法的结果对于均质边坡总体上是一致的,尽管需要进一步的工作来分析含有非均质土壤的边坡[5]。
1 有限元与极限平衡法简介
有限元法(FEM)是科学与工程中求解微分方程或边值问题的一种数值方法。PLAXIS版本8.0是一个用于岩土工程变形和稳定性二维分析的有限元软件包。该程序可以分析人工或自然边坡的问题。使用/c折减法确定安全系数,在该方法中,土壤的强度参数(tan/)和(c)依次减小,直到结构发生破坏。
极限平衡法(LEM)应用完全塑性莫尔-库仑准则,在岩土工程问题中得到了广泛的应用。该方法是一种纯粹的数值静态分析技术,用于根据基本的3个平衡方程保持质量平衡。自1866年Culmann首次尝试用数学方法处理边坡稳定性问题以来,在这一领域进行了大量的研究。
2 影响边坡稳定性的因素
一般来说,边坡稳定性分析最重要的因素是:
①斜坡的几何形状;②土壤的材料特性;③作用在斜坡上的力。研究考虑了3个不同的均质和非均质边坡实例,考虑了:ⓐ快速下降;ⓑ不排水黏土;ⓒ裂缝位置的影响。
a)这项研究将只关注快速下降,因为这是一个更为关键的情况,突然排水会降低储层边缘的稳定性,因为孔隙水压力没有足够的时间稳定下来。
b)不排水黏土边坡是一种特殊情况,因为土壤颗粒的摩擦剪切强度通常很低。细粒土的快速加载将使孔隙中的水消散。在这些条件下,饱和样品的内摩擦角假定为零。
c)滑动头上的拉伸裂纹的存在是不稳定问题的一个重要指标。这些裂缝可能充满水(例如,由于降雨)。在低抗拉强度的黏性土壤中,它们可以变得显著,特别是在减少破坏面长度时,剪切强度可以沿着破坏面移动。
文章使用PLAXIS版本8(FEM软件包)和SAS-MCT版本4(LEM软件包)对这3个条件进行了分析。
2.1 快速下降条件的影响
图1显示了高度为10 m的2:1(64)均质简单边坡的边坡几何结构。分析了不同的(C/H)比值(0.10、0.15和0.20)和不同的摩擦角值(:12、20、30和40)对边坡的影响。考虑了从0.01到1.0的(C/H)范围和从12到40的摩擦角()。从0%(当水库水满且土壤完全饱和)到100%(当水库放空但土壤完全饱和)进行了快速下降分析。如图1所示,在初始水位(H)时水位高度等于斜坡高度(下降0%),而在最终水位(Hw)时水位高度为零(下降100%)。
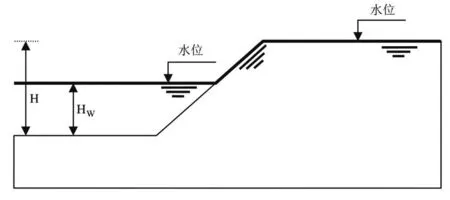
图1 水位快速下降
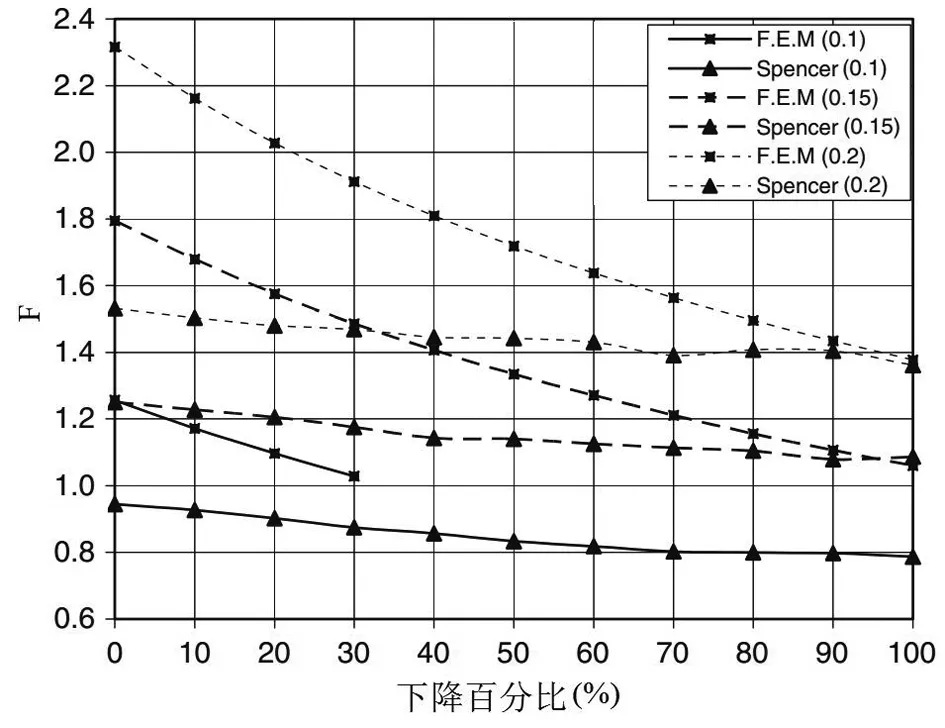
图2 Spencer和FEM的比较(= 12°;C/H= 0.1,0.15,0.2)
图(2)显示了在低水位下降条件下,不同比率和摩擦角为12°的安全系数降低的类似一般趋势,尽管曲率取决于使用的方法;Spencer法给出的安全系数值低于有限元法。在高下降率的情况下,Spencer方法和FEM方法的数值几乎相同。这表明安全系数的值是由水的重量控制的。与有限元法相比,用Spencer法(假定所有切片的切片间力的倾角相同)得到的结果不那么保守。所有C/H比(0.10、0.15和0.20)和摩擦角(12、20、30和40°)都得到了类似的结果:
2.2 不排水黏性土对边坡破坏的影响
本例边坡几何如图3所示,其中边坡高度为6m,两层土壤容重1=2=20kN/m3,不排水摩擦角为U1=U2=0。

图3 实施例2的斜坡几何形状
分析了不同CU1/H比(0.15、0.2、0.25和0.3)下的实例。计算了不同比例的Cu2/Cu1从0.5到3的基础层(CU2)和Bishop的方法,用于确定极限平衡方法的安全系数,假设临界滑动面的形状是圆形的。
图4显示了CU1/H比值为0.2和不同CU2/CU1比值时获得的结果。有限元分析表明,随着CU2/CU1比值从0.5增加到3.0,安全系数呈增加趋势;LEM分析表明,随着CU2/CU1比值增加到1.5,安全系数趋于恒定。
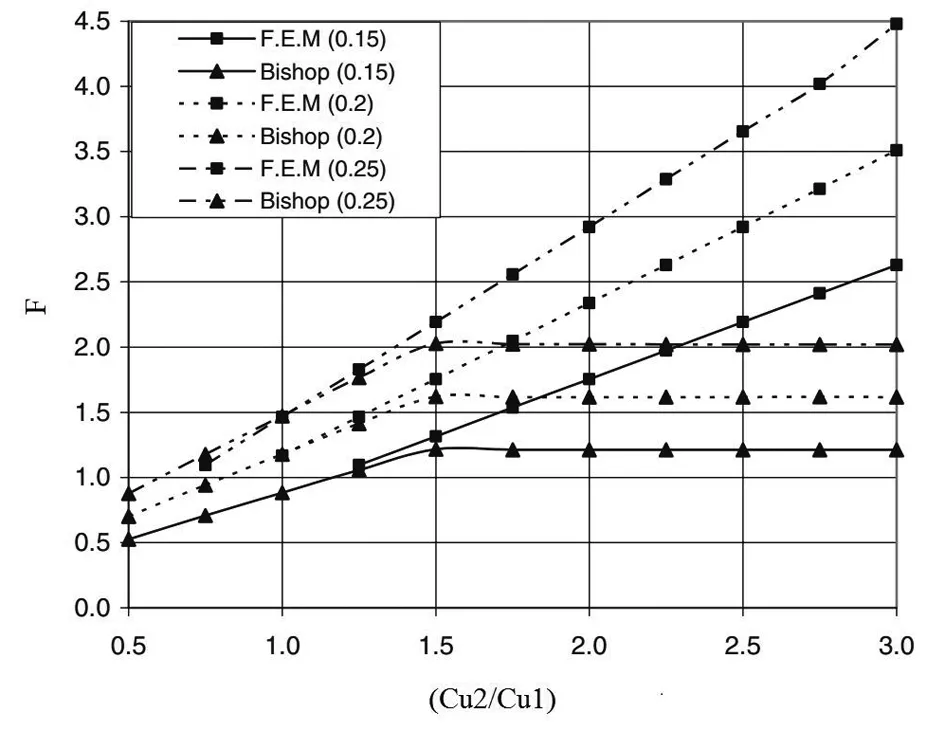
图4 FEM和Bishop结果的比较;CU1/H=0.15,0.2,0.25
一般来说,从两种方法获得的安全系数非常相似,见图),但当CU2远大于CU1时,使用FEM得到的直线角度大于LEM。同样,这些结果适用于分析中使用的所有CU1/H比率。
2.3 裂纹位置效应
图6所示为本例的坡度几何结构。在有水位的情况下,斜坡由四个不同的土层组成。各土层的物理性质见表1。在LEM分析中,采用了Spencer方法和非圆滑动面。在陡坡后面的不同位置(S=5、10、15、20、25、30和35m)放置张力裂缝。拉伸裂纹深度为5m。

表1 土层物理性质
如图7所示,使用LEM时,安全系数随着与陡坎距离的增加而增加,而FEM产生的线保持有效恒定。
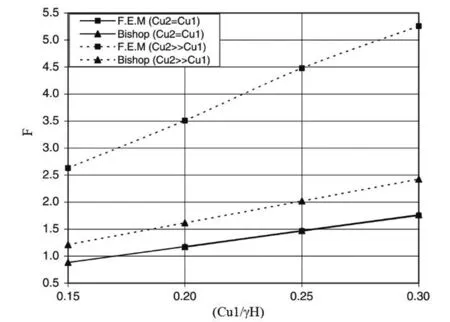
图5 FEM 和Bishop结果比较
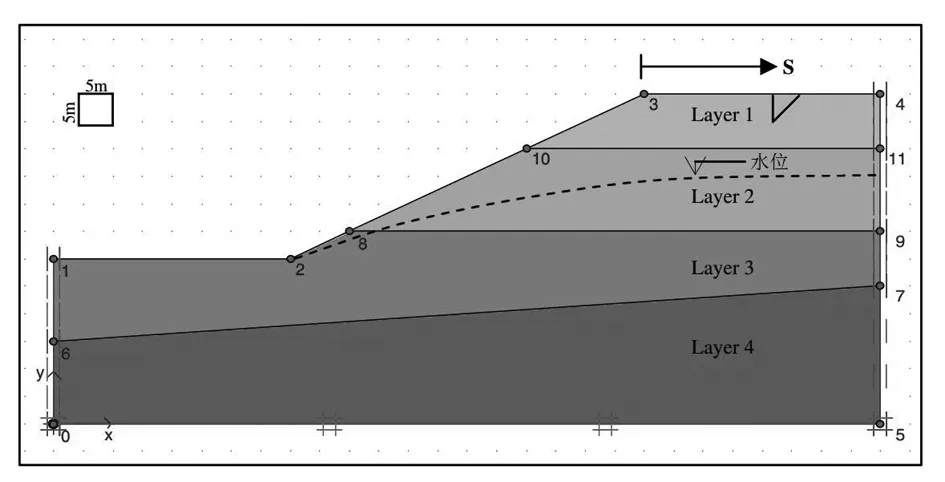
图6 斜坡几何形状和裂缝位置在斜坡上的应用
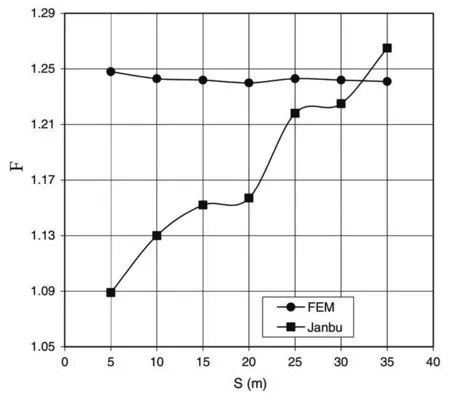
图7 不同裂纹位置的FEM和Janbu结果比较
2.4 结果分析
采用有限元法和有限元法研究了均质和非均质土边坡的稳定性。考虑了快速降深、不排水黏土和裂缝位置的影响。用这两种方法分析了具有任意规则和不规则几何的3个不同的边坡实例。表2显示了从FEM和LEM获得的安全系数值之间的比较;可以看出,获得的安全系数值之间的差异很小。

表2 从FEM和LEM获得的安全系数值的比较
3 结 论
本研究支持先前的工作,指出使用有限元法和各种有限元法所得的安全系数之间存在差异。在文章报告的情况下,两种方法给出的边坡临界滑动面形状和位置几乎相同,但不排水黏土边坡的情况下,有限元法无法定位临界滑动面。当拉伸裂纹包含在不同位置时,有限元法不能充分反映其重要性。
有限元法提供了一种自动搜索临界极限荷载及其相关上下限分析的机制。与使用网格法或随机滑动面生成程序(如SAS-MCT程序)的LEM相比,这被认为是一个真正的好处。对于LEM,在开始搜索或分析两种形状之前,有必要确定临界滑动面(圆形或非圆形)的形状;对于FEM,这是一个自动化的过程。
鉴于所得安全系数值的差异,建议工程师使用有限元法和有限元法分析临界边坡。
