风载荷作用下倾斜塔板压降的数值模拟
2020-12-11张平,王豪,秦然
张 平, 王 豪, 秦 然
(沈阳化工大学 机械与动力工程学院, 辽宁 沈阳 110142)
板式塔广泛应用于精馏和吸收装置,是分离过程中的主要设备,化工生产离不开分离过程,其直接影响最终产品的生产效率和质量品质[1].
板式塔内的气相通过没有液层的塔板,所造成的阻力损失,称为塔板的干板压降[2].板式塔在设计任务规定下的气、液负荷下能否正常操作,需要验算塔板压降、降液管内泡沫液层高度、液体在降液管内停留时间、雾沫夹带量及漏液点等.干板压降是评定塔板流体力学性能的重要指标,其大小影响塔设备的运行状态,同时与精馏塔的传质效率以及生产能力都有密切的联系[3-4].
近年来计算流体力学得到越来越多的应用.王学平等[5]应用FLUENT软件对分离器内部流场进行了数值研究,效果较好.TANG等[6]利用Realizablek-ε模型数值模拟了一种旋流筛板的干板压降与气相流场的分布情况,模拟结果与实验结果基本吻合.李俊峰[7]等对不同规格筛板填料的压降进行了实验测试,并利用Realizablek-ε模型进行了数值模拟,揭示了气相流量、塔板开孔率、塔板板厚、填料板间距等对塔板压降的影响.王晓晗等[8]模拟不同气体动能因子下的文氏棒塔的塔板压降,结论是标准k-ε湍流模型和Realizablek-ε湍流模型与实验结果比较接近.张平等[9-10]数值模拟了不同空塔气相动能因子下水平筛孔塔板的干板压降,发现利用RNGk-ε湍流模型数值模拟塔板压降更为准确.
板式塔属于长径比较大且只有底端固定的直立设备,在风载荷等横向载荷的作用下塔体产生一定的挠曲,塔板发生倾斜[11].风对塔体既可以产生动载荷,也可以产生静载荷,动载荷引起塔体的振动,静载荷使塔体倾斜挠曲,本文研究风载荷产生的静载荷对塔体的影响.干板压降是由气相通过筛孔的突然收缩而又突然扩张的阻力引起的,塔板的筛孔在塔板倾斜时,通道发生改变,塔板压降发生相应的改变.
本文分别用标准k-ε湍流模型和RNGk-ε湍流模型封闭了欧拉方程,数值计算了风载荷作用下倾斜塔板的干板压降.在不同空塔气速的条件下,将数值计算结果同实验结果进行了分析.利用RNGk-ε模型数值计算了空塔气速下,塔板倾角从0°增加4°时,筛孔塔板的干板压降.利用倾斜塔板的压降数据,得到了塔板阻力系数与塔板倾角的关系.
1 数学模型
1.1 控制方程
三维不可压缩流场的连续方程和动量方程为:
(1)
(2)
1.2 湍流方程
标准k-ε模型的k方程和ε方程分别为:
(3)
(4)
RNGk-ε模型的k方程和ε方程分别为:
(5)
(6)
2 物理模型
2.1 计算模型与网格划分
塔体高度不同,塔板倾角不同,采用其中的一块塔板进行数值模拟,改变塔板的倾角的大小.倾斜塔板的数值计算模型及坐标系设置如图1所示,图中X方向为塔板倾斜方向,Z方向为气相流动方向.气相入口为模型的下表面.
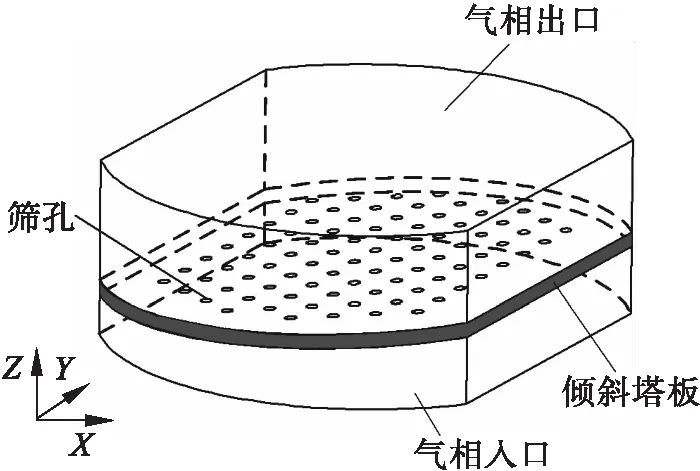
图1 倾斜塔板模型及坐标系
用于数值计算的倾斜塔板的结构参数见表1.表1中塔板上高度表示倾斜塔板上面计算模型的高度,塔板下高度表示倾斜塔板下面计算模型的高度.塔板上、下高度的选取参考文献[12].
利用FLUENT软件数值计算风载荷下倾斜塔板干板压降,模型采用非结构六面体贴体网格.合理的网格大小和划分,不仅保证模拟计算的收敛、稳定和正确,而且还能节约计算的时间.通过对倾斜塔板模型网格的无关性检验,得到模型X方向和Y方向的网格为2 mm,Z方向的网格为5 mm,网格大小对计算结果的影响可以忽略.为了保证模型的计算精度,对塔板厚度方向和筛孔处进行了网格加密,网格大小为1.5 mm×1.5 mm×1.5 mm.整个计算模型的网格总数大约为15×105个.
2.2 边界条件
风载荷作用下倾斜塔板数值模拟的边界条件设置如表2所示.

表2 数值模拟的边界条件
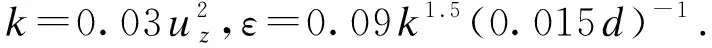
3 实验装置及实验
3.1 冷模实验塔
图2为冷模实验塔装置的结构示意图,装置中的塔板3和塔板4用于实验操作,塔板2为液相均布板,塔板5为气相均布板,保证进入实验装置的气相和液相均匀分布.
1,7 压差计 2 塔板 3.4 测量塔板 5 气相均布板 6 调节螺钉 8 流量计 9 阀门 10 气泵
3.2 实验过程
倾斜塔板干板压降实验过程中只有气相参与工作.为了防止气相由降液管溢出,实验开始前,将降液管封死.调节冷模塔左右的调节螺钉6使塔板处于水平位置.实验开始时首先打开气泵,气相的流量利用流量计8测量,实验塔板4的干板压降数值利用压差计7测量,调节阀门9测量不同空塔气速时的塔板压降.关闭气泵,调整调节螺钉的高度,使塔板倾斜,测量塔板在不同倾斜角度下,不同空塔气速时的塔板压降.
4 计算结果与分析
4.1 模型验证
在塔板倾角θ为2°、塔板厚度δ为5 mm、筛孔开孔率φ为6.5 %时,标准k-ε模型和RNGk-ε模型的数值模拟结果与图2所示实验装置所得结果的对比如图3所示.由图3中可以看出,实验测得的数据与RNGk-ε模型的结果更为接近,与标准k-ε模型的结果相差较大.这说明在不同空塔气速的条件下,利用RNGk-ε模型数值模拟倾斜塔板的干板压降是可行的.

图3 两种计算模型的数值同实验结果的对比
4.2 模拟结果分析
塔体挠曲时,每层塔板的倾斜角度是不同的,因此对不同塔板倾角都进行了模拟计算.塔顶倾角超过5°,塔顶挠度超出许用挠度,研究没有意义.空塔气速分别在0.1~0.5 m·s-1、塔板倾角在0°~4°时,利用RNGk-ε模型数值模拟了倾斜塔板的干板压降,模拟结果如图4所示.从图4中可以看出:空塔气速较小时,塔板倾角对干板压降影响不大;随着气速的增加,干板压降增加,空塔气速较高时,塔板从0°到1°之间增加比较大.
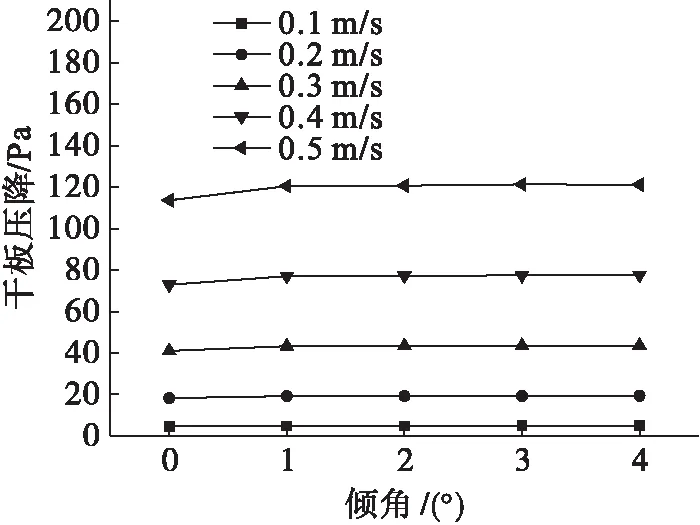
图4 不同空塔气速下干板压降随倾角的变化
塔板干板阻力系数的概念是在20世纪70年代提出的,阻力系数与塔板压降的关系可以表达为
(7)
图5给出的是倾斜塔板阻力系数随塔板倾角的变化曲线.
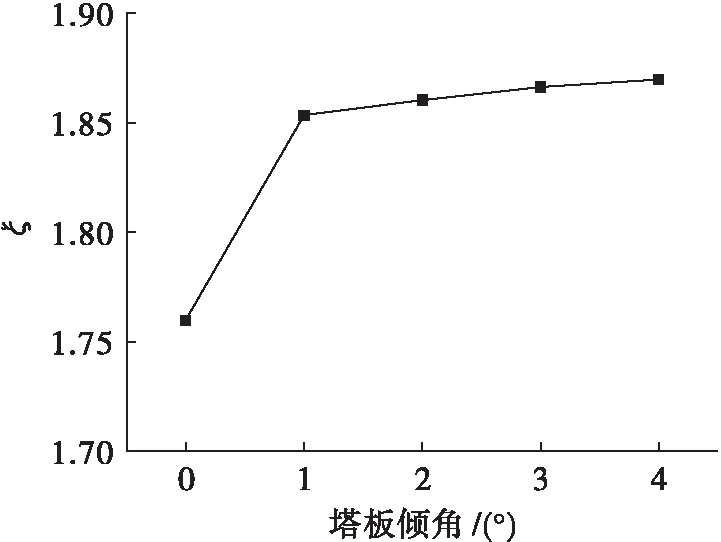
图5 塔板阻力系数随塔板倾角的变化曲线
从图5中可以看出:塔板倾角由0°到1°时,塔板阻力系数增加比较明显,增加5.3 %;而塔板倾角由1°到4°时,塔板阻力系数增加缓慢,只增加0.8 %.这说明塔板刚发生倾斜时,塔板倾角对塔板阻力系数影响较大.
5 结 论
(1)利用标准k-ε模型和RNGk-ε模型计算了不同空塔气速、下筛孔塔板的干板压降.结果表明,RNGk-ε模型的计算结果与实验数据吻合较好,标准k-ε模型的计算结果同实验结果相差较大.
(2)利用RNGk-ε模型数值计算了风载荷作用下不同倾角塔板的干板压降.结果表明,塔板倾斜角度由0°到1°时,塔板压降增加较大,塔板阻力系数也增加较大.随着倾角的不断加大,阻力系数的增加有所减缓.
符号说明:
ui,uj— 速度分量,m·s-1
xi,xj—坐标分量,mm
t—时间,s
μ—动力粘度,Pa·s
ξ— 塔板阻力系数
F— 体积力,N
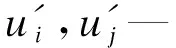
ρ— 密度,kg/m3
μt— 湍动粘度,Pa·s
k— 湍动能,m2·s-2
ε— 湍动能耗散率,m2·s-3
u0— 筛孔气速,m·s-1
Δpd— 塔板干板压降,Pa
