SPGAPSO-SVM：一种城市公交客流量预测算法

林 浩，李雷孝，王 慧

1(内蒙古工业大学 数据科学与应用学院，呼和浩特 010080) 2(内蒙古自治区基于大数据的软件服务工程技术研究中心，呼和浩特 010080)

1 引 言

在现代交通系统中，城市公交交通发挥着重要职能.相对于其他出行方式，公共交通具有载客量大、排污量小、成本较低等优势.为了保障城市公交高效有序的运营，不仅需要良好的公交运营管理方案，有效的运营调度同样必不可少.利用公交相关信息数据进行准确公交客流量预测可以为城市公交车的运营调度提供有效的决策支持.

目前国内外学者在公交客流量预测领域已经取得了一定的研究成果，研究成果可分为两类，一类是用数学方法建立数学规划模型或线性预测模型来实现对城市公交客流量的预测.文献[1]利用多元线性回归方法建立公交车各个时间段的客流量预测模型，并通过城市一卡通数据对模型进行了验证[1].文献[2]采用乘积差分整合移动平均自回归模型(Autoregressive Integrated Moving Average model，ARIMA)对城市轨道交通的客流量进行预测，实验结果表明该模型具有良好的适用性[2].另一类是通过机器学习的相关算法构建预测模型，利用训练数据对模型进行训练，从而预测出客流量.文献[3]使用长短时记忆网络(Long Short-Term Memory，LSTM)实现对多个公交站点的客流量预测，并分析出多个站点的客流量数据间存在相关性[3].文献[4]采用基于黄金分割的粒子群算法对支持向量机(Support Vector Machine，SVM)的参数进行寻优，构建了混合核SVM客流量预测模型[4].文献[5]根据径向基(Radial Basis Function，RBF)神经网络的特点构建了多尺度RBF神经网络的客流量预测模型.实验结果显示，RBF神经网络的学习速度快于BP神经网络，更适用于客流量预测领域[5].

由于公交客流量日间变化较大，其数据具有非线性、非平稳性、潮汐性等特点[6].而SVM作为经典的机器学习算法之一，通过寻求结构风险最小化(Structural Risk Minimization，SRM)来最小化实际风险，能够较好地解决非线性数据、小样本和维数灾难等问题[7].故本文采用SVM进行城市公交客流量预测.SVM算法的性能受其核函数以及核函数参数值的影响.针对传统SVM预测模型准确率不高的问题，本文在SVM的参数寻优阶段采用基于遗传算法(Genetic Algorithm，GA)和粒子群算法(Particle Swarm Optimization，PSO)的混合启发式算法辅助SVM确定核函数参数.混合启发式算法相比单一启发式算法，计算量必定更大，耗时必定更长.针对混合启发式算法速度较慢的问题，分析了影响算法速度的原因，对混合启发式算法基于Spark平台进行了并行化设计，并以此提出了SPGAPSO-SVM算法.使用SPGAPSO-SVM算法训练公交客流量预测模型，进而预测公交客流量可以在提高预测准确率的同时减少算法运行时间，进一步提高公交客流量预测的效率.

2 SVM算法优化

2.1 支持向量机

支持向量机是Vapnik等提出的一种基于统计学习理论的机器学习方法，根据用途可分为支持向量回归机(SVR)和支持向量分类机(SVC).基本思想是在空间中寻求最优分类面，使得距离超平面最远的样本点之间距离最大.设n个样本集为{((xi,y1)|i=1,2,…,n)}，xi∈Rn，其中xi为输入样本，yi为输出样本.此时的决策边界超平面表示如公式(1)所示.

ωTxi+b=0

(1)

通常样本往往是非线性且不可分的，故需引入惩罚因子C与松弛因子ξ，从而得到非线性SVM，如公式(2)所示.

(2)

其中惩罚因子C的作用是调整误差，其取值决定了模型因为离群点而带来的损失.针对公式(2)所描述的非线性问题，可以通过引入核方法(KernelTrick)解决.RBF核是实际中最常用的核函数，其对应的映射函数可以将样本空间映射至高维空间，RBF的解析式如公式(3)所示.

(3)

g为核函数半径，是RBF函数自带的一个参数.g隐含地决定了数据映射到新特征空间后的分布，g越大，支持向量越少，而支持向量的个数又影响着训练与预测的速度.g和公式(3)中σ的关系如公式(4)所示.

(4)

惩罚因子C与核函数半径g是SVM模型两个非常重要的参数，C和g的取值很大程度上决定了SVM模型的复杂程度和性能.为了优化SVM模型性能，提高回归预测准确率，本文采用GA和PSO混合优化算法辅助SVM寻找最优的C与g.

2.2 遗传算法优化支持向量机

遗传算法是Holland等人受达尔文进化论的启发，通过模拟自然界和生物进化而被提出的一种元启发式算法.GA过程简单，多用于函数优化、数据挖掘、机器学习等领域.但GA的种群个体没有记忆，遗传操作盲目无方向，故所需要的收敛时间更长.

对于SVM参数寻优问题，二进制编码是最常用的编码方法.二进制的编码、解码操作简单易行；交叉、变异操作便于实现.遗传算法通过适应度函数评价每一组参数的适应度，来引导迭代过程向好的方向进行.计算适应度后，根据个体的适应度选择个体，并借助于组合交叉和变异等操作，产生出新的解集种群.

2.3 粒子群算法优化支持向量机

PSO是Eberhart博士和Kennedy博士于1995年提出的一种元启发式算法.该算法的思路源于鸟群捕食行为，通过群体中个体之间的信息传递和信息共享来寻找最优解.相较于其他优化算法，PSO参数选取简单、收敛速度快，但是PSO也存在着精度较低、易发散等缺点.

PSO同样使用适应度评价粒子的优劣程度，通过适应度函数寻找个体极值和全局极值，随后根据公式(5)、公式(6)更新各粒子的速度及位置.

v=v1+c1r1(pbest-xi)+c2r2(Gbest-xi)

(5)

x=xi-vi

(6)

在公式(5)、公式(6)中，v是更新后粒子速度；x是更新后粒子位置；vi是粒子当前速度；xi是粒子当前位置；c1和c2分别为学习因子；r1和r2为(0，1)之间的随机数；pbest为个体极值；Gbest为全局极值.公式(5)中3项相加反映了粒子间的信息共享，通过个体的经验和种群的经验来决定下一步活动.

2.4 GAPSO-SVM预测模型

单一智能算法优化SVM在解决复杂问题时存在许多不足，利用算法之间互补性的混合算法成为近年来的研究热点.启发式算法的混合大体上可分为3类：串行式混合，嵌入式混合，并行式混合.本文根据文献[8]，总结PSO算法和GA算法的混合方式、优势和应用如表1所示[8].

表1 PSO和GA的混合方式、优势和应用Table 1 Hybrid mode，advantages and applicationscenario of PSO and GA

由表1可知，并行式混合适用于参数优化等问题.GA和PSO同为元启发式算法，二者均具有智能性和随机性.并且GA和PSO都有种群、适应度函数、更新操作、迭代操作等概念，可以共用一个种群，且均具有并行性.GA比PSO种群更多样，搜索更全面；PSO比GA算法思想更简单，收敛更快速.将GA和PSO结合成GAPSO-SVM算法，两者的异同点使得两种算法在性能上可以克服局限性，实现互补[9,10].

2.4.1 GAPSO-SVM算法设计

SVM参数寻优问题的关键是寻找最优的C与g[11]，因此SVM参数寻优问题的数学模型可以表示为：

P={gbest，Cbest}

(7)

GAPSO-SVM算法将种群分成两部分，分别进行GA操作和PSO操作，每次迭代比较出两者中较优值作为本次迭代的结果进入下次迭代，如公式(8)、公式(9)所示.

(8)

(9)

利用GA和PSO都是通过迭代寻优的共性，将两个算法混合并共用一个最优个体，迭代中充分利用GA的搜索范围大和PSO快速收敛的能力.将参数寻优后得到C与g作为SVM的运行参数输入，训练新的SVM预测模型，进而可求出SVM预测模型的准确率Accuracy.将Accuracy定义为SVM参数寻优问题的目标函数，则可将GAPSO-SVM算法参数寻优问题描述为：

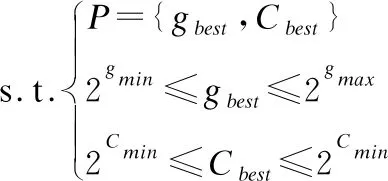
(10)

其中gmin和gmax为RBF核参数g的变化范围，Cmin和Cmin为惩罚参数的C变化范围.最后判断所得结果是否满足终止条件.当满足终止条件时，终止GAPSO-SVM算法的迭代.终止条件如公式(11)所示.

min{fitnessgabest,fitnesspsobest}≤fitnessmin
orT≤Tmax

(11)

其中finessmin为最小适应度，即可接受的最小误差，T为迭代次数，Tmax为最大迭代次数.

GAPSO-SVM算法根据训练数据规模将实验数据切分为训练集和测试集.对初始种群分别进行GA操作和PSO操作，如果当次迭代GA适应度优于PSO适应度，则将GA的最优个体保存下来用到下一次迭代中.当二者的最小值小于最小的适应度或迭代次数超过了最大迭代次数，则终止迭代，返回最优C、最优g作为SVM运行参数.

2.4.2 GAPSO-SVM算法耗时分析

GAPSO-SVM算法的GA操作和PSO操作均可分为初始化种群、种群更新、计算适应度3部分.初始化种群部分包括参数初始化、随机生成初始化种群、计算初始化种群适应度.种群更新部分包括选择操作、交叉操作、变异操作、速度更新、位置更新、种群更新.计算适应度部分包括遍历种群中的所有个体，并调用svm_train函数计算个体适应度.分别运行GA操作和PSO操作20次，其中最大迭代次数为50，种群规模为20，计算并记录各部分消耗时间的平均值.运行结果如图1所示.

图1 GAPSO-SVM算法各部分耗时Fig.1 Time consumptionabout each part of GAPSO-SVM

由图1可知，针对GAPSO-SVM算法而言，种群内所有个体适应度的计算约占总体算法运行时间的91.4%，计算逻辑较为复杂的种群更新耗时约占总体算法运行时间的5.72%，初始化种群约占总体算法运行时间的3.4%.计算适应度耗时过长是因为每个个体都需要进行一次交叉验证来计算样本均方误差(Mean Square Error，MSE).如最大迭代次数为50，种群规模为20，交叉验证参数为5，则要进行5000次交叉验证.

针对计算适应度消耗时间过长的问题，本文将采用Spark平台对算法进行并行化处理来减少计算适应度运行时间.

3 SPGAPSO-SVM算法的提出

与GA-SVM、PSO-SVM等单一算法优化SVM相比，GAPSO-SVM算法逻辑更加复杂，计算量必然更大，算法运行时间也必然更长，尤其是计算适应度阶段[12].所以本文将GAPSO-SVM算法基于Spark平台进行并行化处理，提出SPGAPSO-SVM算法，以提高算法的运行速度.

3.1 Spark平台

Spark是专为大规模数据处理而设计的快速通用的计算引擎.Spark拥有MapReduce所具有的优点，并且中间输出结果可以保存在内存中.因此Spark能更好地结合数据挖掘与机器学习等需要迭代的MapReduce的算法.在内存计算下，Spark比Hadoop快100倍；在硬盘计算下，Spark比Hadoop快10倍[13].

3.2 SPGAPSO-SVM算法设计

SPGAPSO-SVM算法设计主要是依赖Spark所特有的弹性分布式数据集(Resilient Distributed Datasets，RDD)来进行种群的构建、切分和并行化处理.针对计算适应度耗时过长的问题，将种群切分为多个子种群，并行计算子种群内个体的适应度.本文采用SVM的MSE作为适应度函数，适应度函数的计算公式如公式(12)所示.

(12)

3.2.1 SPGA操作

在SPGA操作开始阶段，首先设置SparkConf参数，用于Spark集群应用提交.使用二进制编码将变量编码成染色体用于随机初始化种群.将种群转化为RDD，通过map(getFitness())并行计算种群内个体的适应度.通过collect()合并所有个体适应度，随后比较出最优适应度.使用轮盘赌方法对当前种群进行选择操作、交叉操作和变异操作以产生新的种群，每个个体进入下一代的概率如公式(13)所示[14].

(13)

反复以上操作直至满足终止条件.算法伪代码如下所示.

算法1.SPGA

输入：conf：Spark初始化参数

lenchrom：染色体长度

bound：染色体取值范围

sizepop：种群规模

k：数据分区个数

pcross：交叉概率

pmutation：变异概率

输出：newChrom：迭代后种群

bestFitness：最优个体适应度

1.ProcedureSPGA(conf，lenchrom，bound，sizepop，k，pcross，pmutation)

2.sc← sparkConf(conf)

3.foriinsizepopdo

4.chrom[i] ← Code(lenchrom，bound)

5.endfor

6.populationRdd←sc.parallelize(chrom，k)

7.times← 0

8.while(minFitness≥bestFitnessortimes≥maxTimes)do

9.FitnessRdd←populationRdd.map(getFitness()，k)

10.fitness←FitnessRdd.collect()

11.bestFitness← min(fitness)

12.newChrom← SelectCrossMutation(chrom，fitness，sizepop，pcross，pmutation)

13.chrom.clear()

14.times←times+ 1

15.endwhile

16.endprocedure

3.2.2 SPPSO操作

SPPSO操作的流程和SPGA操作的流程相似.首先设置SparkConf参数，并随机初始化个体位置和速度.将种群转化为RDD，再通过map(getFitness())并行计算种群内个体的适应度.SPPSO中适应度函数与SPGA中适应度函数相同，这样便于比较两种算法产生的解集种群.通过collect()合并所有个体适应度.以当前种群为基础，据公式(5)、公式(6)更新个体位置和速度，随后比较出个体最优适应度和全局最优适应度[15].反复以上操作直至满足终止条件.算法具体伪代码如下所示.

图2 SPGAPSO-SVM算法Fig.2 Flow chart of SPGAPSO-SVM

算法2.SPPSO

输入：conf：Spark初始化参数

popmax：粒子位置上界

popmin：粒子位置下界

sizepop：种群规模

k：数据分区个数

Vmax：粒子最大速度

Vmin：粒子最小速度

c：学习因子

输出：newPop：迭代后种群

bestFitness：最优个体适应度

1.ProcedureSPPSO(conf，popmax，popmin，sizepop，k，Vmax，Vmin，c)

2.sc← sparkConf(conf)

3.foriinsizepopdo

4.pop[i] ←np.random.rand(2)* (popmax-popmin)+popmin

5.V[i] ←np.random.rand(2)* (Vmax-Vmin)+Vmin

6.endfor

7.populationRdd←sc.parallelize(pop，k)

8.times← 0

9.while(minFitness≥bestFitnessortimes≥maxTimes)do

10.FitnessRdd←populationRdd.map(getFitness()，k)

11.fitness←FitnessRdd.collect()

12.bestFitness，bestFitnessForPop← min(fitness)

13.newPop，V← PopVelocityUpdate(pop，V，c)

14.Pop.clear()

15.times←times+ 1

16.endwhile

17.endprocedure

4 相关实验与结果分析

4.1 实验环境

本文利用libSVM(libraryforsupportvectormachines，LIBSVM)实现SVM，编程语言为Python.libSVM是一个支持向量机的软件库，是由台湾大学林智仁教授研发的SVM分类与回归的软件包，其高效易用性得到了广泛认可[16].

本文通过虚拟机搭建的8个节点的Spark集群来验证SPGAPSO-SVM算法性能，每个节点CPU数量为1，节点内存为1G.集群详细配置为：CentOS-6.10-x64，Spark-2.1.1-bin-hadoop2.7，hadoop-2.7.2.tar，pyspark-2.3.2，py4j-0.10.8.1，libSVM-3.2.3.SPGAPSO-SVM算法的参数设置如表2所示.

4.2 数据预处理

本文收集广州市19路公交车2018年1月-6月6个月(20180101-20180631)的IC卡交易数据作为所用的实验数据. 广州市19路的运行时间为06时-22时30分， 故本文只对该时间段预测.原始数据共有10个字段，包括交易时间、线路名称、卡片ID等信息.

表2 SPGAPSO-SVM算法参数设置Table 2 Parameters setting of SPPSO

为了提高数据挖掘的质量，需要利用Spark对数据进行预处理[17].首先通过rdd：[(str，str)] = rdd1.zip(rdd2)将数据整合为key-value的RDD，其中key为线路编号，value为交易时间；然后通过rdd= filter(lambda keyValue：str(keyValue[0])== Line_name)将客流量信息根据线路编号分组.在节假日期间，城市公交客流量相较平日有明显不同，以旅游、购物为目的的出行将明显增多.因此，需通过rdd= filter(lambda keyValue：lp<= keyValue[1] <= up)将节假日的数据去掉以提高预测的准确率.由于SVM对零一之间的数据较为敏感，训练速度较快，故对数据进行归一化处理[18].常用的基于极值归一化公式如公式(14)所示.

(14)

其中X为原始数据，Xmax、Xmin分别为原始数据集的最大值和最小值.

使用libSVM作为SVM的实现工具，还需要将进行筛选过的数据整理为libSVM的输入格式.libSVM的输入格式如下.

Label index 1：value index2：value index3：value

对于客流量预测，Label应为目标值，index是以1开始的整数，value为训练数据.

4.3 实验结果分析

4.3.1 算法准确率和效率

算法准确率采用平均绝对百分误差(MAPE)和均方误差(MSE)评价，算法效率是指算法执行速度的快慢，使用算法程序运行消耗的时间衡量.

在上述实验环境下，采用Python语言对SVM、PSO-SVM、GA-SVM和SPGAPSO-SVM算法进行了实现，并将这4种算法运行效果进行对比，以此验证算法的准确率和效率.采用4.2中经过预处理的数据，将每个算法分别运行20次，计算并记录其中MAPE的最优值、最差值和平均值.运行结果如表3和图3所示.

表3 算法的准确率对比Table 3 Accuracy comparison of algorithms

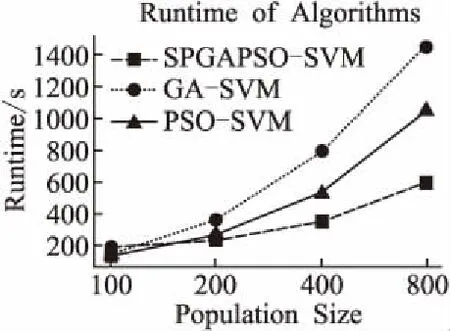
图3 算法的运行时间对比Fig.3 Running time comparison of algorithms

由表3可以看出，针对客流量预测问题，传统SVM算法预测准确率稳定在79%；PSO-SVM的最差值与最优值相差接近4%，这表明PSO-SVM陷入局部最优的概率很高且非常不稳定；GA-SVM的表现优于PSO-SVM，平均准确率为85.5%左右；SPGAPSO-SVM算法相比PSO-SVM和GA-SVM准确率更好，并且平均最优值与最差值相差更小证明了其寻优稳定性更佳，整体预测准确率可以达到86.71%.实验结果表明本文提出的SPGAPSO-SVM算法在客流量预测的准确性上优于其他方法.

对于GA和PSO来说，种群的大小决定了整体算法的计算量.由图3可以看出，在计算量小的情况下，SPGAPSO-SVM算法运行所用时间最长.这是因为申请资源、启动作业、划分任务等基础消耗时间大于每个节点任务的计算时间.随着计算量的增加，3个算法的运行时间呈近线性增加，并行计算的优势越来越明显，SPGAPSO-SVM算法运行所用时间将远远少于GA-SVM和PSO-SVM.实验结果验证了本文提出的SPGAPSO-SVM算法比GA-SVM和PSO-SVM运行速度更快，算法运行所用时间更短，计算效率更高.

本文利用Python语言实现了RBF神经网络和LSTM作为典型机器学习算法与本文提出的算法进行对比.其中LSTM的学习率为0.01、timestep为32、batchsize为5，RBF神经网络的参数通过网格搜索确定，计算结果如表4所示.

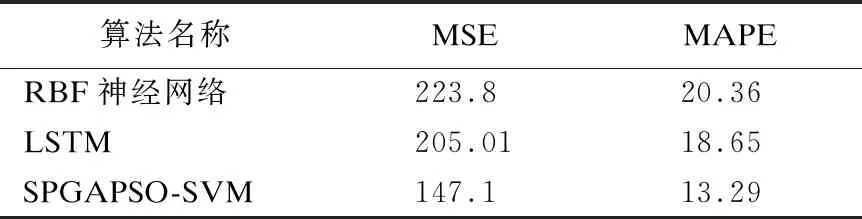
表4 SPGAPSO-SVM与典型机器学习算法对比Table 4 Comparison between SPGAPSO-SVM and othertypical machine learning algorithms

由表4可知，本文提出的SPGAPSO-SVM算法的预测效果优于RBF神经网络和LSTM.

4.3.2 收敛曲线对比实验

收敛曲线对比实验使用均方误差(MSE)作为评价指标，用于观察SPGAPSO-SVM算法在每次迭代中SPGA操作和SPPSO操作的误差变化和参数寻优的整体收敛速度，从而验证混合算法的是否跳出了局部最优.在8个节点的集群中运行SPGAPSO-SVM算法，其中种群大小为100，最大迭代次数为50，记录每次迭代的MSE.运行结果如图4所示.

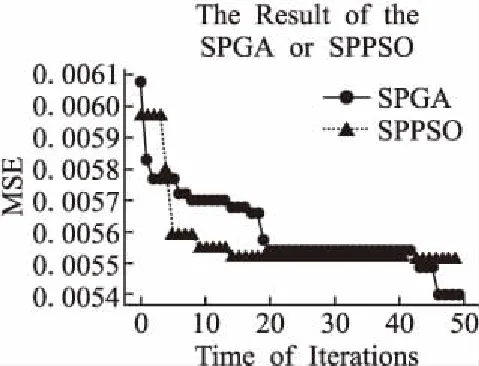
图4 SPGA操作和SPPSO操作的收敛曲线Fig.4 Convergence curve of SPGA and SPPSO

从图4可以看出，算法在20代以前收敛速度较快，算法在20代以后收敛速度逐渐变慢.在迭代开始阶段，SPGA操作帮助整体算法跳出了局部最优.在第5次迭代时，SPGA操作陷入了局部最优，而SPPSO操作帮助整体算法跳出了局部最优；在第42次迭代时，SPGA操作再次帮助整体算法跳出局部最优；至此参数寻优算法在最大迭代次数的限制下收敛至全局最优解.实验结果验证了SPGAPSO-SVM算法与GA-SVM、PSO-SVM等单一算法优化SVM相比具有两个优点：SPGAPSO-SVM算法可以有效克服GA-SVM、PSO-SVM等单一算法优化SVM易陷入局部最优的问题，预测的准确率更高；在最小适应度相同的情况下，SPGAPSO-SVM算法比GA-SVM、PSO-SVM等单一算法优化SVM所需的迭代次数更少.

4.3.3 算法可扩展性验证

算法可扩展性实验用于测试是否可以通过增加节点来提高算法运行速度.实验基于单个节点、2个节点、4个节点和8个节点，采用4.2中经过预处理的数据，将SPGAPSO-SVM算法运行20次，计算并记录平均值和加速比.运行结果如图5和图6所示.

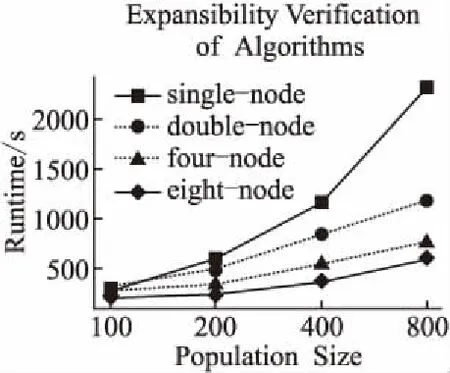
图5 SPGAPSO-SVM算法可扩展性实验Fig.5 Experiments on scalability of SPGAPSO-SVM

由图5可以看出，随着计算量逐步增加运行时间呈线性增长.当种群大小为100时，单个节点、2个节点、4个节点和8个节点差别较小.这是因为多节点集群运行程序时，需要申请资源、启动作业、划分任务和分配资源等操作，存在一定的基础消耗.随着计算量的增大，8个节点的运行时间将远远低于4个节点、2个节点和单个节点.这是因为节点数越多，每个计算节点负责处理的计算量就越小.

加速比是同一个任务串行运行时间和并行运行时间的比值，是衡量可扩展性的一个重要指标.由图6可以看出，在计算量小的情况下，加速效果不明显，这是因为集群基础消耗的时间较多，集群未发挥到理想的效果.随着计算量的逐步增加，加速比呈增长趋势并逐渐趋于理想值.通过上述实验结果分析，进一步说明了SPGAPSO-SVM算法具有较好的可扩展性.

图6 SPGAPSO-SVM算法加速比实验Fig.6 Speedup experiment of SPGAPSO-SVM

4.3.4 客流量预测结果

使用4.2中经过预处理的数据作为实验数据，采用SPGAPSO-SVM算法对数据集最后14天(20180617-20180630)06时-22时的公交客流量进行预测，共224小时.将每小时的预测结果按时间顺序拼接，预测结果与真实值对比如图7所示.

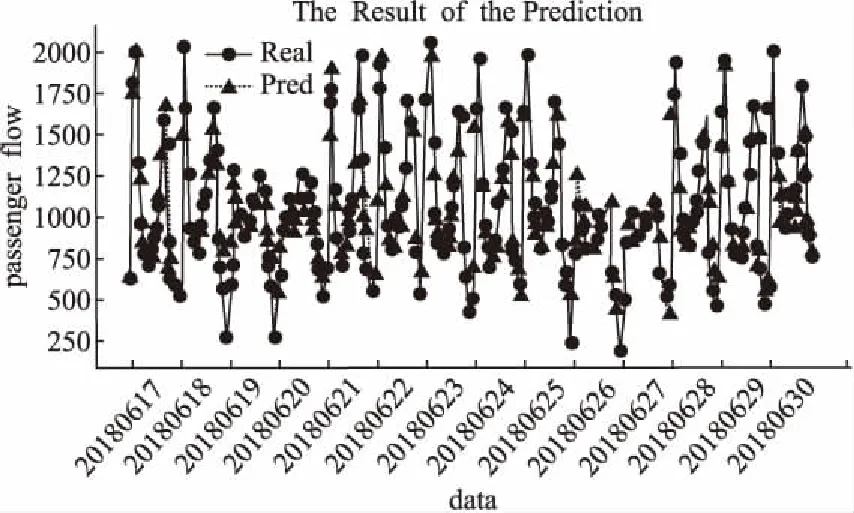
图7 客流量预测值与实际值对比Fig.7 Comparisons between predicted passenger flow and real passenger flow

通过图7可以看出，SPGAPSO-SVM算法对高峰期客流量预测有较高的准确率，对低谷期客流量预测存在一定偏差.当次整体预测准确率为86.71%，当次参数寻优后最优为0.68，最优为15.4873.

5 结 论

本文在对公交客流量预测领域相关研究成果进行深入分析研究的基础上，针对GAPSO-SVM算法复杂度较高和运行速度过慢的问题，对GAPSO-SVM算法基于Spark平台进行了并行化处理，提出SPGAPSO-SVM算法，该算法有效提高了运行速度和效率.选取2018年广州市19路公交车6个月的IC卡交易数据作为实验数据，并根据实际需求对该数据集进行了预处理，设计GAPSO-SVM算法耗时分析、SPGAPSO-SVM算法准确率和效率、算法可扩展性等多组实验对SPGAPSO-SVM算法进行了验证.实验结果表明，SPGAPSO-SVM算法具有较高的预测准确率、较快的运行速度和良好的可扩展性，预测效果由优于RBF神经网络和LSTM等传统机器学习算法.