一种基于差分进化改进的深度神经网络并行化方法
2020-12-11朱光宇谢在鹏朱跃龙
朱光宇,谢在鹏,朱跃龙
(河海大学 计算机与信息学院,南京 211100)
1 引 言
神经网络[1]是对于人脑认知能力的近似和模拟,通过模仿生物神经网络的特性来处理各类非线性复杂问题.多年来,神经网络在模式识别、图像处理、语音识别、文本处理、目标检测、人脸识别等多个领域取得巨大成就[2-7].
神经网络在高速发展的同时也面临着挑战[8].目前已有的深度神经网络,其网络模型结构及相应参数量日趋庞大.在如此复杂的网络模型下,训练数据量增长的同时,往往带来的是训练过程中各类计算量的指数增长,这也意味着传统在单机上进行训练的方式变得缓慢而又沉重,其所引起的后果将是巨大的时间成本开销和训练质量的下降[9,10].因此,研究者们[11-20]提出了多种针对神经网络并行化改进的方法,其所关注的问题主要包括两个方面:一是如何通过并行化方式加速模型收敛进程,减少训练时间;二是在并行化过程中如何提高训练模型的精度,减少因并行化所带来的模型精度下降.
2 相关工作
为了解决神经网络训练效率的问题,研究者们提出了多种并行化策略,如表1所列,具体可分为两类:硬件架构层面的改进和软件体系层面的改进.

表1 神经网络并行化策略Table 1 Parallel strategies of neural network
在过去一段时间,虽然CPU性能得到较大提升,但依旧难以支撑复杂的深度神经网络模型训练,研究者们开始将模型训练所依托的硬件体系重心转向其他高并行度、高吞吐量的硬件架构以提高模型训练过程中的并行处理能力.文献[11]提出在多GPU下的并行优化策略,提高GPU利用率的同时减少数据传输开销.文献[12]将神经网络模型分别在CPU,GPU,ASIC,FPGA上进行了实现并做出了比较,实验结果表明,FPGA和ASIC表现的性能远优于CPU和GPU,相比之下ASIC效率更高一些,但FPGA具备更加灵活的策略.虽然硬件可以在一定程度上提高神经网络的效率,但是成本较高,而且需要对现有架构做较大的改变,如何寻求当前分布式架构下的一种高效方法更加经济科学.
各种并行模型及各类算法的出现使这一问题得到有效改善.文献[13]和文献[14]分别通过MapReduce及Spark模型实现了神经网络的数据并行化训练.文献[15]提出一种基于差分进化的并行方案,但仅对算法内部计算适应度的过程进行了并行化.文献[16]提出在神经网络数据并行化过程中,阶段性地获取每个子模型,然后通过参数平均法得到一个全局模型并分发给各子节点进行后续训练.文献[17]提出一种基于模型平均的框架,与文献[16]不同,仅当每个子模型训练至收敛后,才取平均后的结果作为最优模型.虽然模型平均是并行训练过程中获取全局模型可行的方案,但得到的全局模型往往效果一般,模型精度甚至低于其子模型,文献[18]对此进行了论证,同时提出了一种压缩算法,该方法获得的全局模型相较于均值方法获得了更高的精度,但增加了额外的学习过程.除了模型精度问题之外,还要考虑由于并行化所带来的额外时间开销问题.文献[19]对深度神经网络在并行化训练过程中的数据通信开销进行了研究,提出了一种自适应量化算法实现了接近线性的加速.文献[20]提出了一种根据数据稀疏性优化数据传输量的混合方法.上述研究均未考虑到并行训练过程中,由于节点计算能力不平衡所造成节点等待的额外时间开销.本文基于以上存在问题提出新的解决方案.
3 深度神经网络与并行化
3.1 深度神经网络
深度神经网络是一个包含输入层、输出层以及多个隐藏层的神经网络,如图1所示.神经网络自底向上逐层完成计算和传递,最终在输出层得到结果,这样一个过程称之为前向计算.
前向计算完成的同时,反向自顶向下通过例如随机梯度下降法来完成参数的更新,如公式(1)所示:
(1)
公式(1)中netj表示神经元ej的输入,δj表示神经元ej的误差敏感度,ai表示神经元ei的输出,η表示学习率,Err表示误差.对训练样本按照上述训练过程进行数轮迭代,每完
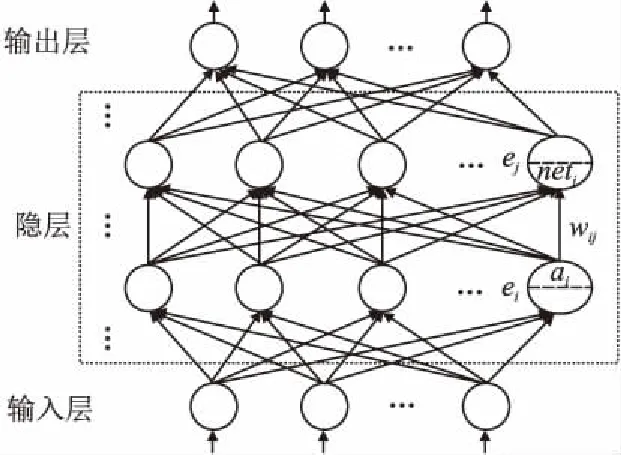
图1 深度神经网络Fig.1 Deep neural network
成一轮训练,模型会得到一次参数更新.训练DNN的目标就是尽可能发挥其非线性逼近能力,使模型朝着正确的方向收敛,从而提高输出结果的精确度.
3.2 并行化
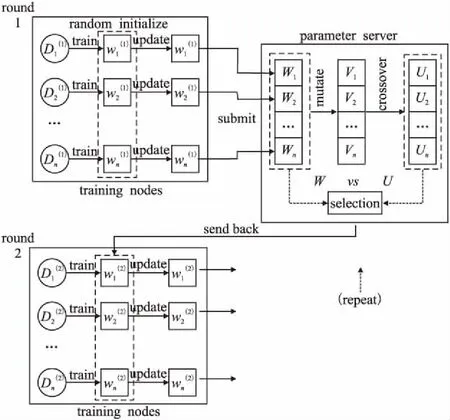
深度神经网络的并行化行式主要包含两类:数据并行化和模型并行化[1,9].模型并行化指将DNN模型内部中各部分结构分别映射到多个节点上实现并行计算,该方式所带来的影响是节点间频繁的数据通信开销.数据并行化指将训练数据划分到多个节点,由各节点分别训练其所获得的本地数据.参数服务器阶段性地收集各节点训练出的本地模型并聚合出一个新的全局模型,再将其分发到各个节点上用于之后的训练.目前采用较多的方式为后者,通过数轮迭代的并行化训练,在达到终止条件后结束获得最终模型,如图2所示.

图2 数据并行化Fig.2 Data parallelism
一个典型的DNN数据并行化训练过程可以被描述为如下步骤:
1)数据划分.训练数据集D被划分成n块分配到集群中的n个训练节点上,D={D1,D2,…,Dn}.
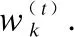
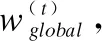
(2)
公式(2)中f(·)为聚合函数,αk为权重.一般常用聚合方法有,model averaging,即取αk=1/n,对模型参数进行平均;回归方法,即单独将聚合过程看作一次线性回归问题,通过学习得到各模型的加权比重.
4)迭代训练.在进行第t+1轮训练前,参数服务器会将上一步得到的全局模型分发给各个节点作为其新一轮训练时的初始本地模型,如公式(3)所示:
(3)
模型按照上述步骤重复进行多轮迭代训练,训练结束后获得最终DNN模型.
4 DE-DNN
本文提出了一种在现有分布式环境下进行深度神经网络并行化训练的方法DE-DNN.该方法提供两种策略从模型和数据两个层面对DNN数据并行化过程进行优化.
4.1 DE模型优化策略
在阶段性的模型聚合过程中通过一般方法得到的新全局模型往往效果一般[18],从而影响整个并行训练过程的收敛速度,本文对该步骤进行改进.差分进化(Differential Evolution,DE)是一类基于群体差异的全局优化方法[21],相较于其他方法[22],具备全局收敛快、算法稳定、结构简单的优点.一个典型的差分进化算法形式为“DE/rand/1/bin”,包括变异、杂交、选择步骤.其基本思想是每次随机选取三个个体,其中两个进行向量差操作后结果加权并与第三个求和来产生新个体,最终通过将适应度高的新个体淘汰适应度低的旧个体来完成种群的更新.本文将基于此对DNN并行训练过程中获取全局模型的关键步骤3进行优化,以达到改善全局模型精度进而加快收敛速度的目的,具体实现见算法1.
算法1.DE模型优化算法
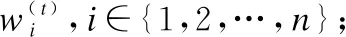

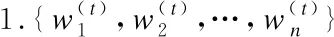
2.forifrom 1 tondo
3. generate new solutions by mutation:

5. generate new solutions by crossover:
6.forjfrom 1 toddo
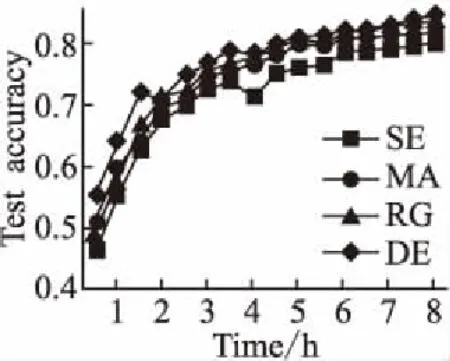
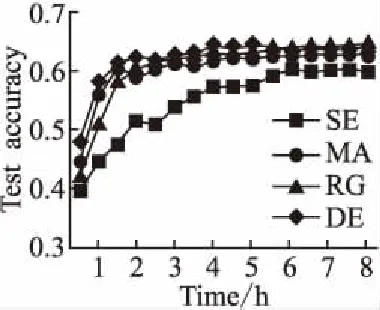
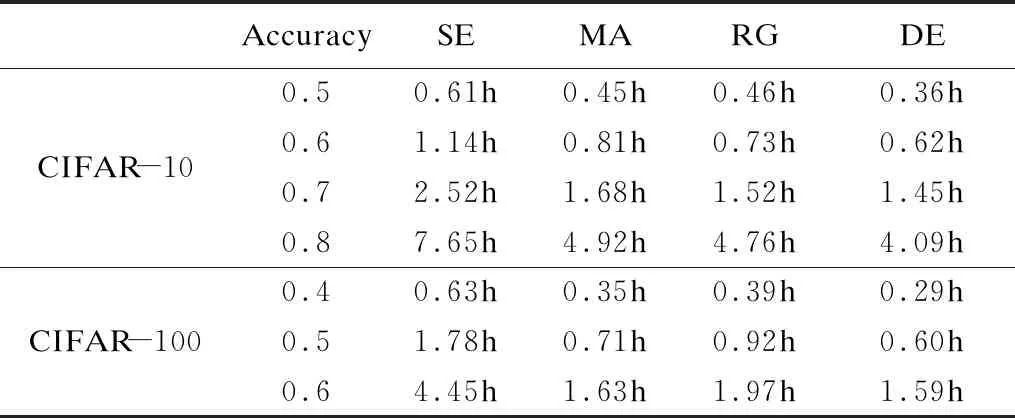
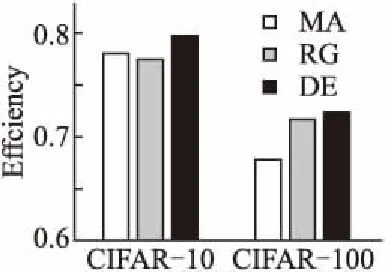
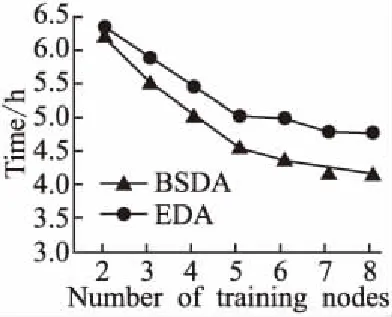
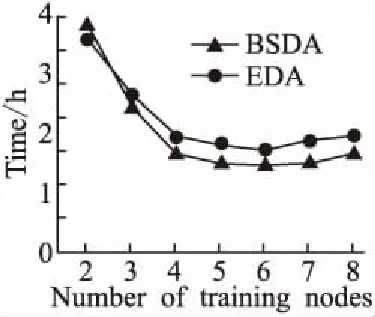
7.ifrandj 9.else 11. get selection for next round: 13.ifAccuu>Accuwthen 15.else 19.end. 假设当前处于第t轮,且各节点已完成本轮的本地训练,算法具体可以描述为以下几个步骤: (4) (5) (6) 往后每一轮各节点完成本地训练后,重复上述步骤,直到达到终止条件,此时参数服务器从当前种群中选择最优个体作为最终模型.整体过程如图3所示. 图3 DE模型优化过程Fig.3 DE model optimization 算法的性能很大程度上取决于缩放因子F和杂交因子CR的设定,由于不同的参数设定会造成不同的影响,我们采用一种自适应控制参数法[23]进行调控,如公式(7、8)所示: (7) (8) 公式(7、8)中randi,i∈{1,2,3,4}是0~1范围内的随机数,代表随机概率;τ1和τ2分别代表调整F和CR的概率.设置τ1=τ2=0.1,Fl=0.1,Fu=0.9.因此,新的缩放因子F是0.1~1范围内的随机值,新的杂交因子CR是0~1范围内的随机值,通过此方式实现了训练过程中每代因子的动态优化. 在现有分布式环境下进行DNN数据并行化同样面临着训练节点计算能力不均的问题.考虑到各节点在同一时段可能存在性能差异,并行训练过程中易出现在某一轮中,已完成本地训练的节点需要等待少数性能不佳的节点完成其本地训练后才可以继续后面工作,从而造成额外的节点等待时间开销,这与数据在各节点分配的数量有关.本文中DE-DNN提出一种新的基于批处理的自适应数据分配策略BSDA,将训练数据逐批次并根据各节点当前性能分配适量的数据,从而实现训练过程中各节点样本数量的动态优化,具体实现见算法2. 算法2.BSDA数据分配算法 输入:训练数据集D,集群节点数n,划分批次m,新批次数据b 输出:新批次数据各节点分配量 1.B{B1,B2…Bm}←divide the data set equally intombatches; 2.ifb=B1then 5.else 7.forifrom 1 tondo 9. predict new training time for roundt+1 by efficiency: 12. develop new divisions forbto each node: 15.end. 假设当前的分布式集群中存在n个训练节点,训练数据总量为d.BSDA将数据分成m个批次,每次只将d/m个数据划分给集群,再由BSDA决定分配到各个节点的数量.首批次分配采用均匀划分,各节点分配到的数据量如公式(9)所示: (9) (10) (11) 以此类推,逐批次为各节点分配适量训练数据,用公式(12)统一表示.每批次各节点分配数据量依据最近一轮各节点训练效率进行裁定,本文称之为自适应分配策略. (12) (13) 文中实验所采用的环境配置如表2所示.实验采用CIFAR-10和CIFAR-100数据集[24]进行测试.CIFAR-10是一个由10类共60000张彩色图像构成的数据集,该数据集中50000张为训练数据,10000张为测试数据.CIFAR-100数据集大小和格式与CIFAR-10相同,但标签为100个类别,每类图像数量仅CIFAR-10数据集的1/10. 表2 实验环境Table 2 Experimental environment 实验中基于NiN[25]深度神经网络模型进行实现,该模型所实现的网络结构如图4所示,各层参数信息见表3,共包含966986个参数.实现过程中,同时采用了随机初始化参数和对网络内部进行Dropout的操作.以上NiN模型及相应操作皆通过TensorFlow实现并应用于CIFAR-10数据集的测试中.而对于CIFAR-100数据集,其所实现的NiN网络模型结构相同,唯一区别是Mlpconv3层会输出100个特征映射. 图4 NiN实验模型Fig.4 NiN experimental model 表3 参数信息Table 3 Parameters information 实验根据目标不同分为两个部分: 1)模型收敛速度实验.在并行化训练过程中,对于阶段性获取全局模型的方法,这里将本文提出的模型优化方法称为DE,同时将一般常用的Model Averaging方法称为MA,回归方法称为RG,对于传统串行训练称为SE.DE方法增加测试F、CR因子的设定对实验产生的影响,对于本文采用的自适应参数控制法称为SA(·),同时测试全过程对F、CR设定固定值产生的结果.实验中会记录不同阶段各方法得到的模型参数以及所用时间,并通过测试集的分类准确率进行实验对照. 2)数据分配方法实验.对DE-DNN采用一般等量分配方法实现,这里称为EDA,并与本文提出的BSDA方法进行实验比较.同时考虑分布式环境下训练节点数量对实验的影响,我们对节点数量进行调整,比较在不同训练节点数量下各方法的训练时间. 实验1结果反映了各阶段,使用传统串行训练SE方法以及并行训练过程中使用DE方法和MA、GR方法得到的全局模型在测试集上的分类准确率.图5、图6分别记录了各方法在CIFAR-10和CIFAR-100数据集上的表现.结果显示,传统SE训练方法在训练各阶段所表现出的模型分类准确率皆远低于三种并行训练方法;DE方法在并行训练过程中,表现出了高于其他方法的分类准确率,在训练中前期收敛速度明显加快,可以在较短时间内收敛到更高精度的全局模型,在后期虽然收敛速度放缓,但依旧表现出较高的分类准确率.为了更直观比较各方法收敛速度,实验过程中记录了各方法训练出的模型在收敛到一定精度时所产生的时间开销,如表4所示.结果表明,对于实验中的两类数据集,DE方法在训练过程中的模型收敛可以产生较少的训练时间. 图5 CIFAR-10测试集准确率 图6 CIFAR-100测试集准确率 表4 各方法达到不同准确率所用时间Table 4 Time for each method to achieve different accuracy 实验中同时比较了并行训练过程中各阶段,参数服务器内不同聚合方法所产生的全局模型是否优于各本地模型的平均水平.即在并行训练各阶段,获得所有本地模型精度和的平均值,并统计各聚合方法获得的全局模型精度大于该平均值次数的比例,本文将该实验指标称为全局模型优越度,用effciency表示,在CIFAR-10和CIFAR-100数据集上分别统计达到0.8和0.6分类准确率时的effciency值.实验结果如图7所示,DE聚合方法在CIFAR-10测试集上全局模型优越度接近0.8,在CIFAR-100上超过0.7,且高于MA和RG方法的effciency值,表明DE方法在并行训练的多数阶段,模型精度总体高于各训练节点的平均水平,有助于在并行化过程中促进全局模型向正确方向收敛,提升训练效率. 图7 全局模型优越度Fig.7 Global model effciency 实验中同时注意到,DE方法在训练过程中所获模型精度时出现波动,为测试算法内部F和CR两个因子的选定对DE过程的影响,表5记录了实验中当F、CR选取固定值时和通过SA(·)动态变化时DE-DNN产生的时间开销.结果表明,当F、CR两个因子在训练全过程始终不变时模型的收敛速度,皆低于动态SA(·)方法;且通过调整两个因子的设定值发现,随着F、CR增大,对训练效率造成的影响越大. 表5 不同FCR因子值所用时间Table 5 Time for different FCR factor values 实验2分别在CIFAR-10和CIFAR-100数据集下进行测试,比较了两种数据分配方法BSDA和EDA所引入的训练时间开销.其中,根据数据集不同,CIFAR-10以分类准确率达到0.8时所引用的时间进行参照,CIFAR-100以分类准确率达到0.6时所引用的时间进行参照.实验中,设置一台参数服务器,分别调整训练节点的数量进行多次测试,比较不同节点数量下各方法的变化情况.实验结果如图8、图9所示. 图8 CIFAR-10训练时间 图9 CIFAR-100训练时间 由实验结果可知,本文提出的BSDA数据分配方法在多训练节点环境下,相较于一般等量分配EDA表现出了更少的训练时间开销,且随着节点数量增多,两种方法的时间差越明显,表明出自适应数据分配策略的优异性.但在少量节点环境下效果一般,图9中显示在仅有两个训练节点的条件下,BSDA较EDA反而产生了更长的时间开销.同时注意到,在训练节点数量大于6后,两种方法对应的时间减少幅度放缓,这表明在一定数据量下,通过增加训练节点数量可以在有效范围内提升效率,但持续增加下去所带来的额外开销也会对整体进程产生制约. 深度神经网络在高速发展的同时面临着训练效率、模型质量等诸多挑战,对于深度神经网络的并行化研究成为热点.在现有分布式环境下进行数据并行化训练是DNN并行化的一种有效方案,但其存在全局模型精度不佳、训练节点性能不平衡的问题.针对该上述问题,本文提出了一种基于差分进化改进的深度神经网络并行化方法DE-DNN.DE-DNN利用差分进化算法全局收敛快、实现简单的优点对DNN并行化训练过程中获取全局模型的关键步骤进行改进和优化;同时提出自适应数据分配算法减少多节点训练过程中的额外等待时间开销.实验中,在CIFAR-10和CIFAR-100数据集上基于NiN深度网络模型对DE-DNN进行了实现和测试.实验结果表明,DE-DNN中提出的DE模型优化方法在训练过程中相较于一般方法SE、MA、RG表现出了更快的收敛速度和更高的全局模型精度;同时,自适应数据分配算法BSDA相较于一般等量分配方法EDA花费了更少的训练时间,减少了因节点性能不平衡所产生的额外等待时间,加速了训练进程.未来我们将基于其他不同复杂程度的神经网络进行实验,并尝试分离出一套通用的DE-DNN框架以适应更多类型的深度神经网络进行并行化接入和测试.





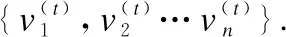
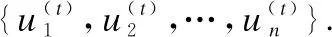
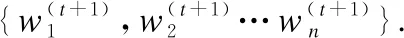
4.2 BSDA数据分配策略

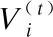
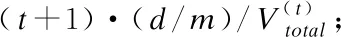

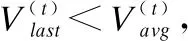
5 实验评估
5.1 实验设置

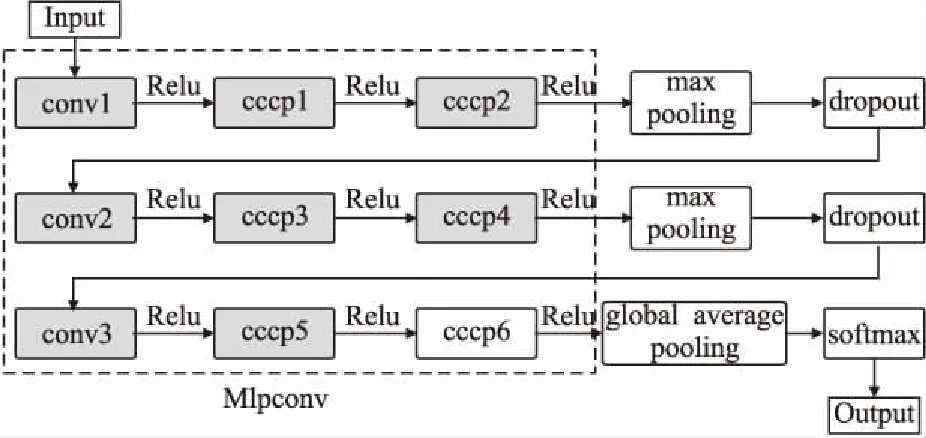
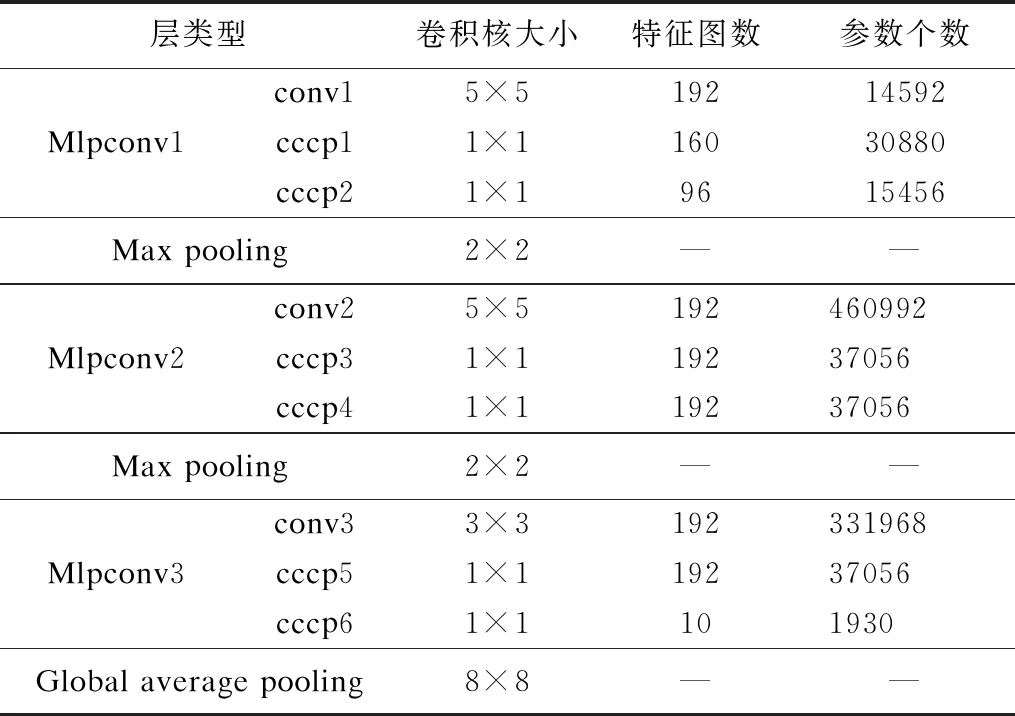
5.2 结果分析

6 总 结
