结合遗传规划和遗传算法的代码异味检测方法
2020-12-11高建华
赵 敏,高建华
(上海师范大学 计算机科学与技术系,上海 200234)
1 引 言
代码异味是由于设计缺陷或不良编码习惯导致深层次质量问题的代码症状,不一定直接地导致软件的错误,但会引起后续的一些可读性差、效率低等系统问题,加大软件维护的难度[1].相关研究报告显示,大型系统的改进、更新以及重组等一系列维护活动占用了软件项目总成本的90%,提前检测并清理这些代码异味,可以帮助程序员很好地理解源代码的同时也节约了项目的成本.
Marinescu、Moha以及Khomh[2-4]等人使用度量、结构和词汇信息的组合来表示代码异味的特征,定义规则来识别代码异味的关键特征.但是在检测特征不明显的代码异味时,精确度不高.在大型的应用场景中,也需要花很多时间对规则做大量的校准工作.
Fokaefs[5]提出了移动重构的方法,这是一种基于度量的代码异味检测方法.该方法用Eclipse插件将问题量化,先通过插件对系统质量进行评估,再重构.此方法仅适用于单一的代码异味.
Fontana[6]等人提出了基于关联的代码异味检测方法,通过代码异味之间的直接关系和传递关系来检测代码异味,但这一方法只能检测一些可量化的代码异味.
Emerson[7]等人提出来一种基于可视化的代码异味检测方法.这一方法将可交互的检测工具和手工识别代码异味相结合,快速地认识和理解代码异味.但此方法涉及到手动标识代码异味的特征,在效率和精确性上没有很大的保证.
对此,本文提出了一种基于协同并行算法优化的代码异味检测方法,即将遗传规划和遗传算法相结合,把代码异味的检测问题看作一个分布式搜索最优解问题.本文又通过Jaccard系数对算法进行优化,降低了检测器的成本,提高了搜索效率.
2 相关术语
2.1 代码异味
代码异味也称设计异常或设计缺陷,是指对软件维护产生不利影响的设计情况,它常常标志着代码应该被重构[8].本文关注以下8种代码异味,如表1所示.

表1 代码异味及其描述Table 1 Code smells and its descriptions
2.2 遗传规划
遗传规划的基本思想是演化候选的程序种群来解决一个特定的问题[9].随机生成候选种群,通过适应度函数对这些种群的质量进行评,如果符合标准则为最优解,反之,则对这些种群进行一系列的交叉、变异等基因操作生成新的种群,迭代至符合标准输出.
2.2.1 检测规则的生成
在评估大量与代码异味检测相关的参数后,确定了检测规则的终端集和函数集,终端集包含不同的质量度量以及阈值,函数集包含不同的逻辑运算符.检测规则是基于抽象语法树从范例中生成的,多用二叉树的形式来表示[10].
1)终端节点A是度量及其阈值的集合.度量包括一些代码的行数、方法的数量、属性的数量、加权方法的数量以及接口数量等.
2)内部节点B是一个逻辑运算符的集合C{AND,OR}.
如图1所示,规则由一个AND-OR树组成.其中,一条候选检测规则对应一条特定的代码异味.
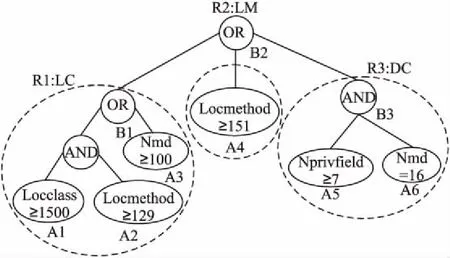
图1 检测规则的表示Fig.1 Representation of detection rules
规则1(R1).如果Locclass≥1500且(AND)Locmethod≥129或(OR)Nmd≥100,代码异味为Lager Class(LC);
规则2(R2).如果Locmethod≥151,代码异味为Long Method(LM);
规则3(R3).如果Locmethod≥7且(AND)Nmd=16,代码异味为Data Clumps(DC).
2.2.2 最优检测规则的生成
遗传规划通过其进化算子(选择、交叉和变异)迭代得到最优检测规则.
1)选择:以保留良好解决方案的基因和提供更好的解决方案为两大原则进行选择.通过适应度函数对检测规则池P进行评估,根据适应度值的高低排序,在池P中挑选出1/2适应度高的检测规则,形成新的检测规则池S(大小为|S|,|S|=1/2|P|);再将池S经过随机的交叉、变异形成新的子代检测规则池E,从子代池E中选出大小跟池P一样的检测规则池O(大小为|O|,|O|=|P|),新的检测规则池U由池P和池O组成,大小为|U|=|P|+|O|=2|P|.
2)交叉:在两个父节点上随机选取他们的子节点及其子树进行交叉,生成的新树结合双方的信息,但仅限于同种代码异味的检测规则.
3)变异:变异通常分为三种情况:当变异算子应用在终端节点时,则将它替换为新的终端节点(质量度量以及阈值);当变异算子应用在功能节点时,则用新的函数来替换;如果是树的变异,则将节点及其子树一并替换为新生成的子树.
2.3 遗传算法
选择、交叉以及变异是遗传算法的三个基本操作.选择,根据定义的适应度函数对种群中个体进行评估,适应度高的种群个体被选择;交叉,根据自然遗传学对被选择的种群个体进行交叉,形成新的个体;变异,在个体基因的基础上按照一定的规则进行变异继而形成新的最优种群个体[11].
2.3.1 检测器的生成
所谓的检测器是指与良好范例代码(几乎没有代码异味的范例代码)的偏差[12].由于本文只对代码的结构感兴趣,所以可将检测器表示为一组谓词序列,谓词序列的每个维度都是一个代码元素,对应面向对象系统中的类(C)、属性(A)、方法(M)、参数(P)、泛型(G)和类之间的方法调用关系(R).
为了方便谓词序列之间的比较,降低相似性计算的复杂度,谓词序列的顺序必须严格按照类、属性、方法、参数、泛型、类之间调用关系的顺序排列.例如,谓词序列CGAAMPPM表示一个具有泛型的类,谓词序列中包含两个属性、两种方法,第一种方法有两个参数,如图2所示.

图2 检测器A的表示Fig.2 Representation of detection A
谓词序列还包含一些相关结构的详细信息,如类型、可见性等.在检测器A中,谓词C是一个类,类名为C12,可见性为public.
2.3.2 最优检测器的生成
遗传算法通过其三个基本操作选择、交叉以及变异,不断迭代搜索得到最优的检测器.
1)选择:检测器的选择算子与检测规则的选择算子相同.
2)交叉:两个父代谓词序列L1、L2,两个子代谓词序列S1、S2.随机选择一个位置p;L1的前p个元素放入S1的前p个元素,L2进行同样的操作;L1剩下的元素放入S2,L2进行同样的操作.例如谓词序列L1:CGAAMPPM和谓词序列L2:CGAMPPR在1/5处进行交叉,得到的新谓词序列S1:CGAAMPR和S2:CGAMPPPM.
3)变异:变异应用在随机改变检测器中元素的参数.例如,图2中检测器A的第一个类的可见性为public,将其可见性变异成private.
2.4 遗传算法与遗传规则的区别
遗传规划是遗传算法的一个分支.由于遗传算法是按照一定字长的字符串形式来描述问题,而遗传规划是以非定长层次结构反映特定的问题.检测器是以谓词序列(字符串)形式呈现,检测规则是用二叉树表示,所以本文将遗传规则和遗传算法分别应用在搜索最优检测规则和最优检测器的问题中.
3 检测规则和检测器的评估
3.1 代码异味范例的覆盖率
设定一个目标函数C,计算实际检测到的代码异味与范例中的代码异味的重叠,覆盖率如公式(1)所示.
(1)
其中:e是范例代码中代码异味的数量,r是执行检测规则后检测到的实际代码异味数量,对于ai(C),如果第i次检测到有code smell存在,ai(C)为1,否则为0,如表2、表3所示.

表2 范例代码中的代码异味Table 2 Code-smells in the base of examples

表3 实际检测的代码异味Table 3 Detected code smells
将表3中检测到的代码异味与表2中代码异味相比,类Senior、Primary以及Junior不是代码异味.类Bachelor是代码异味但代码异味的类型不对.只有类Doctor是真正的代码异味.所以,代码异味范例的覆盖率为(1/3+1/5)/2=0.26.
3.2 检测器的成本
设定一个成本函数Cost来评估检测器的质量.其中,S为检测器组,检测器Si的成本是其通用性和重叠的缺失的加权平均数,如公式(2)所示.
(2)
通用性的缺失是通过计算检测器Si的谓词序列与良好范例代码中类Cj的谓词序列相似性而来,如公式(3)所示.
(3)
重叠的缺失是通过计算检测器Si的谓词序列与检测器组S中所有其他检测器Sj的谓词序列的相似性而来,如公式(4)和式(5)所示.
(4)
其中,sim()如公式(5)所示.
(5)
a,b为谓词序列A和B的长度,Sa,b为A和B的公共最长子序列.
为了计算两个谓词序列之间的相似性,本文将Needleman-Wunsch算法应用到全文,并使用Jaccard系数对其进行优化.
Needleman-Wunsch算法是一种动态编程方法,它是在允许加入空隙的情况下,找到两个序列之间的最优全局对齐[13].对齐序列(a1,…,an)和序列(b1,…,bn)时,根据下面的式(6)计算出Needleman-Wunsch算法矩阵LCS,并通过回溯写出匹配字符串.其中,LCS矩阵第一行和第一列都为0;
ai=bj;
LCS(i,j)=LCS(i-1,j-1)+Sim(A,B)
ai≠bj;

(6)
Jaccard系数是计算两个样本集合之间的相似性[15,16],如公式(7)所示.
(7)
如图3所示,检测器A的第一个方法Method(C12,m154,void,Y,public)与范例代码34中的第一个方法Method(Options,isFractionalMetrics,boolean,Y,public)相比,N、Y都为变量名,public是可见性,所以用Jaccard系数计算为2/(5+5-2)=0.2.
本文设定了一个风险评估适应度函数,将风险评分超过0.75的片段认为是代码异味,如式(8)所示.
(8)
其中,ei是待评估的代码片段.
3.3 检测规则和检测器的交叉函数
如果一个类被检测规则和检测器同时检测到,那么该类是代码异味的几率就会很大.因此,本文将检测规则和检测器组合来检测代码异味.

图3 Jaccard系数计算图Fig.3 Calculation figure of the Jaccard index
在每一次的迭代中,从最优检测规则和最优检测器中选出一组检测规则和检测器,应用在新的系统N中.本文构造了一个最优解决方案矩阵M,行是最优检测规则MPi,列是最优检测器MAj,最优检测规则和最优检测器的交叉点得分,如公式(9)所示.
(9)
对于新系统N中,由最优检测规则检测出含有代码异味类的集合为Cr={c1,c2,…,ci};由最优检测器检测出含有代码异味类的集合为Cd={c1,c2,…,cj};实际检测出含有代码异味类的个数为T.

图4 交叉点得分的说明Fig.4 Illustration of the intersection score
如图4所示,待评估系统有5个类,其中有2个类存在代码异味.将4个最优检测规则和4个最优检测器在待评估系统上运行,并得到一个4×4的矩阵,检测规则R18检测出2个类存在代码异味,检测器检S11测出3个类的risk值都高于0.75,所以3个类都存在代码异味.计算两种解决方案的交叉点得分依据式(9)为:(2/3+2/2)/2=0.83.
检测器S11与4种检测规则的交叉得分点分别为:0.43、0.83、0.59以及0.64.分析交叉得分点可知S11与R18的交叉得分点最高,在检测代码异味时,将其视作一组可能的最优解决方案.
其中,每一种解决方案的交叉适应度函数如公式(10)所示.
finter(MPi)=Min{finter(MPi,MA∀j)}
finter(MPj)=Min{finter(MP∀i,MAj)}
(10)
3.4 检测规则质量的评估
检测规则的适应度函数基于:
1)最大概率地覆盖代码异味的范例;
2)使用与检测器并行执行的交叉函数,使得一致性达到最大.
基于以上两点,检测规则质量的适应度函数如公式(11)所示.
(11)
3.5 检测器质量的评估
检测器的适应度函数基于:
1)减小范例代码与检测器之间的相似性,从而提高检测器的通用性;
2)减小检测器之间的重叠,即两个检测器的相似性.
基于以上两点,检测器质量的适应度函数如公式(12)所示.
(12)
4 基于协同并行算法优化的代码异味检测方法
4.1 改进的Needleman-Wunsch算法
在文献[16]中提出了一种改进的Needleman-Wunsch算法,普通的Needleman-Wunsch算法只比较谓词的相似度,改进的Needleman-Wunsch算法通过式(13)进一步计算谓词的参数的相似性,精确了最长公共子序列的长度,如公式(13)所示.
(13)
其中,ai、bj是两个谓词的参数集,p、q是两个谓词的参数.
以检测器A中谓词Method参数集(C12,m154,void,Y,public)和范例代码34的谓词Method参数集(Options,isFractionalMetrics,boolean,Y,public)为例,式(13)计算得出两种方法的相似性为:2/5=0.4.改进后的LCS矩阵如公式(6)所示,其中Sim(A,B)=PMij.
4.2 基于Jaccard系数的Needleman-Wunsch算法
为了更进一步地提高检测器的通用性和降低检测器之间的重叠,本文在改进的Needleman-Wunsch算法基础上,提出基于Jaccard系数的Needleman-Wunsch算法,用于对比计算两个谓词的参数集.
以检测器A中谓词Method参数集(C12,m154,void,Y,public)和范例代码34中的谓词Method参数集(Options,isFractionalMetrics,boolean,Y,public)为例,由Jaccard系数计算出来两个谓词参数集的相似度0.2.改进后得到计算LCS矩阵如公式(6)所示,其中Sim(A,B)=J(A,B).两种方法的对比如图5所示.
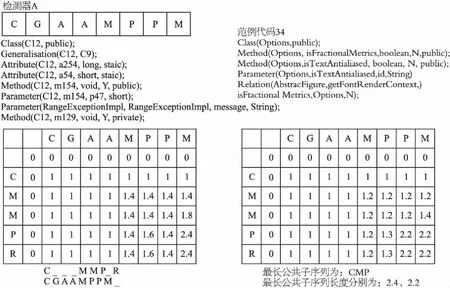
图5 两种方法的对比图Fig.5 Comparisonfigureof two methods
根据以上两个公式计算出来的最长公共子序列分别为2.4和2.2,将结果带入式(5),可得到检测器A和代码范例34的相似度Sim()分别为0.4和0.2.由式(3)可得,检测器和范例代码之间相似度的精确可以提高检测器的通用性;由式(4)可见,检测器间相似度的精确可以降低检测器之间的重叠;由式(2)可得,随着检测器通用性的提高和检测器间重叠的降低,检测器的成本也随之减少.后续本文对这两种方法在同一数据集上进行验证,以说明基于Jaccard系数的Needleman-Wunsch算法要优于改进的的Needleman-Wunsch算法.
4.3 协同并行算法优化
为了减少搜索时间、精确检测结果,本文提出将最优检测规则和最优检测器并行应用在检测过程中,该并行算法的具体实现过程如算法1和算法2所示.
算法1.基于遗传规划的最优检测规则获取算法
输入:代码质量度量集合M
手工评估的系统集合S(异味示例)
新系统A
输出:最优检测规则
1.Max_size=100;
2.gen=0;%Counter
3.NBS=100;%number of best Soulution
4.MaxGen=500;%maximum no.fo generation
5.R1=rules(M,Smell_type);
6.P1=set_of(R1);
7.Initial_population_GP(P1,Max_size);
8.While gen 9. for each R1∈P1 do 10. detected_smells_GP(S)=excute_rules(R1,S); 11. fitness(R1)=compare(detected_smells,smells_examples); 12. end for 13. best_sol_P1=select(P1,NBS); 14. send(best_sol_P1); 15. best_sol_P2=receive(best_sol_P2); 16. for each R1∈best_sol_P1 do 17. detected_smells_GP(A)=excute_rules(R1,A); 18. fitness_intersection(R1)=Max_intersection(detected_smells_GP(A,R1)∩detected_smells_GA(A,best_sol_P2) 19. fitness(R1):=update fitness(R1,fitness_intersection); 20. end for 21. gen=gen+1; 22.end 23.retum best solution rules; 算法2.基于遗传算法的最优检测器获取算法 输入:良好示例代码的集合GES 新系统A 输出:最优检测器 1.Max_size=100; 2.gen=0;%Counter 3.NBS=100;%number of best Soulution 4.MaxGen=500;%maximum no.fo generation 5.R2=detectors(GES); 6.P2=set_of(R2); 7.Initial_population_GP(P2,Max_size); 8.While gen 9. for each R2∈P2 do 10. fitness(R2)=cost(R2); 12. end for 13. best_sol_P2=select(P2,NBS); 14. send(best_sol_P2); 15. best_sol_P1=receive(best_sol_P1); 16. for each R2∈best_sol_P2 do 17. detected_smells_GA(A)=excute_rules(R2,A); 18. fitness_intersection(R2)=Max_intersection(detected_smells_GA(A,R2)∩detected_smells_GP(A,best_sol_P1) 19. fitness(R2):=update fitness(R2,fitness_intersection); 20. end for 21. gen=gen+1; 22.end 23.retum best solution rules; 算法1和算法2并行执行,并在每一代中使用适应度函数进行交互.第1-3行构造一个初始检测规则种群和检测器种群;第4-15行是搜索最优检测规则和检测器的循环过程;第16-20行是两种算法的交互. 在每次迭代中,本文使用适应度函数对每个个体进行质量评估.在评估检测器时(算法2的第10行),对原先的适应度函数进行了改进.本文使用Jaccard系数对Needleman-Wunsch算法进行改进,从而增加了检测器的通用性和检测器之间的重叠,减小了检测器的成本.5.2中的实验结果表明,这种改进不仅增加了代码异味的精度和召回率,还减少了搜索时间. 图6 方法的概图Fig.6 Overviewof the proposed approach 如图6所示,协同并行算法优化可以理解为以下4个步骤: 1)通过遗传规则和遗传算法并行搜索最优检测规则和最优检测器; 2)将搜索得到的最优检测规则和最优检测器应用在新系统上; 3)根据交叉点得分更改最优检测规则和最优检测器的适应度函数,生成最优解决方案. 4)达到先前设定的固定迭代次数后,停止. 为了评估基于协同并行算法优化的代码异味检测的方法,本实验从大型开源系统中提取8个开源项目对8种代码异味进行实验,并与基于单一种群的算法以及文献[16]中的协同并行算法进行比较. 本实验从现有的数据集[17]中挑选出类大小不的开源项目,其包含了近800种手动识别的代码异味,如表4所示. 在过去的十多年中,这些项目一直保持着活跃的状态,并包含了大量的代码异味.此外,这些项目被诸多研究引用,分布于不同的应用领域,其包含的代码异味已被大量相关研究明确检测和分析[16]. 表4 实验项目Table 4 Systems for experiment 本实验将剩余的项目作为代码异味范例来生成检测规则,例如检测GanttProject3,则选择剩余的项目作为代码异味范例来生成规则.从范例中可以生成特定项目的特定的规则,所以在同一软件项目内,规则是适用的[10]. 对于检测规则的充分性,范例库中包含了研究的所有代码异味类型,所以范例具有充分性.规则是从范例中生成,范例的充分性从一定程度上也保证了规则的充分性[10]. 对于检测规则的一般性,Decor[3]是公认的可用于生产环境的经典代码异味检测工具.在参考文献[10]中,将从范例中生成规则的方法与Decor行对比,实验表明前者的精度与召回都要优于后者. 本实验选择JHotdraw[18]作为良好的代码异味范例,并通过与JHotdraw之间的偏差来生成检测器,因为JHotdraw包含很少的已知代码异味. 本文根据文献[19]提出的种群数和迭代数,将遗传规则和遗传算法的种群数固定在100,迭代数固定在1000.协同并行算法优化的种群数固定在100,迭代数固定在500.并将基于遗传规划、遗传算法、协同并行算法以及协同并行算法优化的方法执行500次进行比较. 为了强调种群的多样性,本实验将进化算子中交叉概率设为0.9,变异概率设为0.5. 为了评估本文方法的准确性,本实验计算了两种度量:精度(PMV)和召回(RMV).在实验中,精度表示所有检测到的代码异味中检测到正确的代码异味的概率,召回表示所有手动识别的代码异味中正确检测到的代码异味的概率. 实验主要寻求以下几个问题的解答: Q1:基于协同并行算法优化,什么类型的代码异味可以被正确的检测? Q2:协同并行算法优化在多大程度上优于基于单一种群的方法以及原来的协同并行算法? 本实验记录了不同项目中基于协同并行优化方法下8种代码异味的精度值和召回率,如表5所示.在不同的项目中,8种代码气味的精度值和召回率都超过了85%.表5结果表明协同并行算法优化的方法没有偏向于检测特定的代码异味.在所有项目中,每个代码异味类型的分布几乎相等.这种不偏向于识别某种特定代码异味的能力是本文方法的一个关键优势.大多数现有的工具和技术在很大程度上依赖于度量的方法,对于FE、SS这些代码异味,度量的方法并不奏效[20,21].从这一方面来看,协同并行算法优化结合了多种不同的检测方法,在代码异味的检测上具有一定的准确性.(Q1) 表5 不同项目下代码异味的精度值和召回率Table 5 Precision median values and recall median values of different projects 实验将4种方法分别应用在不同的项目上,每种方法运行51次,并计算精度值和召回率. 表6 不同方法下的精度值和召回率Table 6 Precision median values and recall median values of different methods 如表6所示,基于遗传规划方法下得到的精度值大约在82%、召回率大约在80%;基于遗传算法方法下得到的精度值大约在82%、召率大约在81%;基于协同并行算法方法下得到的精度值大约在89%、召回率大约在87%;基于协同并行算法优化方法下得到的精度值大约在91%、召回率大约在88%;从纵向来看,随着项目大小的改变,精度值和召回率并没有很大的浮动,可以表明精度值以及召回率与项目大小无关.从整体来看,基于单一种群的算法的精度和召回率低于基于协同并行算法,基于协同并行算法优化方法的精度值和召回率最高,可以表明基于协同并行算法优化的方法优于其余两种基于单一种群以及基于协调并行算法的方法.(Q1) 将基于协同并行算法优化的代码异味检测方法和两个基于单一种群以及基于协同并行算法的代码异味检测方法,分别应用在不同的项目上. 图7 不同项目上的平均执行时间比较Fig.7 Average execution time comparison on the different project 如图7所示,从CUP时间来看,基于协同并行算法优化的执行时间是基于单一种群的一半.因此,在代码异味检测的问题上,并行执行比单一执行耗时更少,基于协同算法优化的执行时间也少于基于协同并行算法.这是因为在优化研究领域中,评估阶段通常是最耗时的,在本实验中,用Jaccard算法优化了用于评估检测器的Needleman-Wuncsh算法,增大了检测器的通用性并减小了检测器之间的重叠,减少搜索时间的同时也减少了评估阶段的耗时.(Q2) 本文提出了基于并行协同算法优化的方法来检测代码异味,降低了检测器的成本,加快了搜索速度.由遗传规划搜索得到最优检测规则,由遗传算法搜索得到最优检测器,再将两种方法在同一项目上运行,找到两种解决方案的交集,其结果是令人信服的.不足之处在于,本文只关注8种代码异味,相对局限,未来将扩大实验规模,以检测更多的代码异味,提高方法的一般适用性.此外,还准备增加并行的算法个数,求证3个及3个以上的算法检测出来的结果会不会更加精确.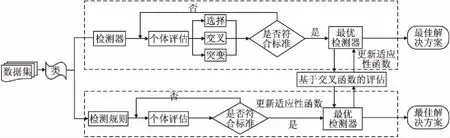
5 实 验
5.1 实验环境

5.2 实验配置
5.3 实验结果与分析



6 期 望
