基于CBOW模型的链路预测方法

赵宇红，张 政

(内蒙古科技大学 信息工程学院，内蒙古 包头 014010)

1 引 言

在网络理论研究中，复杂网络是由数量众多的节点和节点之间错综复杂的关系共同构成的网络[1].复杂网络拥有众多形式，既不是完全规则，也不是完全随机.现实世界中存在的网络一般都是复杂网络，比如常见的电力网络、航空网络、计算机网络以及社交网络等.复杂网络的研究是网络研究中的一大热点，而链路预测能够对复杂网络中的缺失信息或隐含信息进行预测，从而有效挖掘和呈现内在的信息与规则，因此吸引着越来越多研究者的关注.

链路预测的目标体现在对于网络中实际存在但是还没有被探测到的链路的预测或对网络中目前不存在，但应该存在或者是未来有可能存在的链路的预测[2].复杂网络中的链路预测是指通过已知的网络节点信息以及网络结构信息等，预测网络中尚未产生连边的两个节点之间产生连接的可能性，在实际应用中有着巨大的价值.例如，在蛋白质相互作用网络中通过链路预测结果指导试验，提高试验的成功率从而降低试验成本[3]；在社交网络中通过链路预测方法对用户进行好友推荐[4]，提高相关网站在用户心中的地位和用户对网站的忠诚度；在电子商务网络中，通过对用户历史行为和购买记录进行分析，为用户推荐相应产品或者电影，在吸引用户、推广产品等方面具有重要的作用[5].

随着计算机硬件技术的进步，计算机运算能力得到巨大提升，人工神经网络算法得以高效率运行，深度学习得到前所未有的发展，使深度学习成为热门的研究方向，其在图像处理、音频处理以及自然语言处理等领域的成功运用为解决链路预测问题带来了启发.文献[6]提出两种模型架构—CBOW(Continuous Bag of Words)和skip-gram，用来计算大规模数据集中的连续词向量表示.对计算得出的结果通过词相似性任务进行评估.两种模型分别通过上下文对中心词进行评估以及通过中心词对上下文进行评估，在自然语言处理中应用十分广泛，且计算成本相对较小.

近年来，链路预测方法仅仅考虑节点自身属性信息或者仅仅考虑节点所处的网络结构信息，这两类方法都只考虑复杂网络中的部分信息.

本文从概率语言模型训练产生的词向量得到启发，向量作为原生信息在空间中的呈现，是信息本质特征的内在表现.网络中的节点可以看作是自然语言处理过程中的词，在网络演化中，节点本身的特性与结构关联将形成节点的上下文信息.为了有效、全面地获取网络中的节点序列信息，将节点序列看作是具有意义的句子，考虑每一个节点出现在节点序列某一位置的概率，提出基于连续词带模型(Continuous Bag of Words，CBOW)的链路预测方法.使用深度优先搜索(DFS)获得包含网络结构信息的节点路径，再结合使用广度优先搜索(BFS)获得的节点n阶邻居信息的节点序列，可以获取节点序列的完整信息.使用CBOW模型通过中心节点的上下文节点序列训练产生节点对应的向量表示.向量的方向与大小是向量的原生信息，因此提出一种节点向量相似性指标—向量自量趋向性(Self-measurement Tendency of Vector，SMTV)，以此指标完成度量并进行链路预测.通过在3个真实网络数据集中进行的对比试验，本文提出的方法相比其他经典算法在预测精确度方面表现更好.

2 相关工作

2.1 基于相似性的链路预测方法

基于相似性的链路预测方法从度量角度不同分为基于节点相似性的预测方法和基于网络结构相似性的预测方法.

2.1.1 基于节点相似性的链路预测

在网络中单纯考虑节点之间属性的相似程度就可以判断两个节点是否相似，属性相似的节点之间更容易连接[7].在网络中刻画节点属性的相似性，最简单直接的方法就是利用节点的标签.比如，网络虚拟身份中的职业、地区、教育程度、兴趣爱好、性别等，利用上述属性在社交网络中进行好友推荐，就可能找到潜在的好友.但是，由于网络自由性和监管问题，在很多情况下，获取网络节点的真实属性信息是不现实的，例如，在社交网络中，个人用户注册的信息可能是虚假的，因此将虚假信息作为节点的属性进行链路预测就变得不可信.

2.1.2 基于网络结构相似性的链路预测

在网络中难以获得真实节点属性信息的时候，一种可行的方法是根据网络结构来计算节点的相似性.如果在网络中两个节点所处的网络结构越相似，那么它们之间存在连边的可能性越大.

基于网络结构信息的相似性预测方法最经典的就是共同邻居(CommonNeighbors，CN)[8]，即两个节点如果有更多的共同邻居，则它们的相似性越高，越有可能产生连边.其公式如公式(1)所示:

(1)

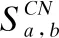
CN方法认为每个共同邻居对于这两个节点的贡献度是相同的，但是，通常共同的邻居节点对于节点的贡献度可能是不同的.一般情况下我们认为度大的共同邻居比度小的共同邻居贡献度小.基于两节点共同邻居的度的信息的Adamic-Adar(AA)指标[9]，根据共同邻居节点的度为每个节点赋予一个权重值，该权重等于节点的度的对数分之一.其公式如公式(2)所示:

(2)

其中kz代表节点z的度.如果节点a和节点b共同邻居节点的度越大，那么该指标分数值越低.

基于共同邻居的相似性指标的优势在于计算复杂度较低，但是由于使用的信息非常有限，预测精度受到限制.例如在Internet路由器网络中，由5000多个节点构成的一千多万节点对中有超过99%的节点对之间的CN相似性分数都是0，剩下的节点对中也有超过90%的节点对分数是1，只有不到5%的分数是2，导致的结果是相似性分数过于集中，节点对之间的区分度太低，链路预测的精度受限[10].周涛等人[11，12]在共同邻居的基础上考虑三阶路径的因素，提出基于局部信息相似性的Local Path(LP)指标.即在考虑共同邻居的基础上，继续考虑两个节点之间通过三条路径即两个节点进行连接的路径条数，结合两者计算两节点之间的相似性，计算公式如公式(3)所示:

(3)

其中α为可调参数，A表示网络的邻接矩阵，(A3)xy表示节点vx和vy之间长度为3的路径数目.

2.2 基于机器学习的链路预测方法

机器学习链路预测方法使用较多的是随机游走算法.文献[13]提出一种基于随机游走的DeepWalk方法，该方法首先在网络上等概率随机采样产生大量的随机游走序列，之后使用模型对随机游走序列中每个局部窗口内的节点对进行概率建模.随机游走就是从某一特定的节点出发，每次游走都从当前节点连接的边集合中选择一条，沿着选定的边移动到下一个节点的过程.利用流式的、短的随机游走，提出了一个通用的语言模型用来探究图结构，根据随机游走中包含的顶点来估计下一个顶点出现的概率，如公式(4)所示：

Pr(vi|(v1，v2，…，vi-1))

(4)

文献[14]提出一种与度分布一致的初始资源分布方法，此方法只考虑有限步长的随机游走过程.从某一节点x出发之后开始进行随机游走，定义πxy(t)为t+1步正好游走到的节点y的概率，得到基于t步随机游走的相似性指标，如公式(5)所示：

sxy(t)=qxπxy(t)+qyπyx(t)

(5)

其中q表示节点的初始化资源分布.通过大量实验比较得出由于此方法采用有限步长的随机游走，因此算法复杂度较低，对于规模较大甚至较稀疏的网络都很适用.

Node2vec[15]对随机游走方法进行了改进，在对网络中的节点进行游走遍历的时候不使用等概率的随机游走，而是使用一种具有回溯并且非均等概率的游走的方式对网络上的节点进行采样.定义了两个参数p，q指导的二阶随机游走概率，如公式(6)所示：

(6)

其中αpq(t,x)表示游走的概率，dtx表示节点x到节点t的边数.通过3个真实世界数据集中的对比实验结果表明Node2vec-Hadamard方法的结果要比单纯使用DeepWalk-Hadamard的方法效果更好.在随机游走过程中，只能考虑节点的某一个邻居节点以及获得一条包含有随机连通信息的路径，对于邻居信息的提取不够完全，对于连通信息的提取也太过随机.

张牧涵等人[16]开发了一种γ衰减启发式理论，将众多链路预测相似性指标函数统一在一个框架中，并证明可以从局部子图中很好地近似这些相似性指标函数，并基于此理论提出图神经网络从局部子图中学习相似性算法的方法.

文献[17]根据相似度的性能改进，提出一种基于引力的无监督链路预测方法，通过集成节点特征、社区信息和图属性来减小预测空间，从而提高局部和全局预测的准确性.

在现有相关研究中，对节点本身的属性和网络结构信息在链路预测共同作用考虑不足，且全面与准确刻画节点的自身及空间信息仍有待改善，本文综合考虑这些问题，提出基于CBOW的链路预测方法—CBOW-SMTV.利用深度优先搜索和广度优先搜索分别获得包含有网络连通信息的节点序列以及节点邻居信息的节点序列，这些节点序列共同构成训练模型的节点序列库.CBOW模型通过考虑节点序列的顺序关系来训练节点序列库从而得到节点的向量表示，以向量的原生特征对节点进行刻画，将节点自身属性信息映射为节点向量自身的模长属性，将两节点的相互关系映射为节点向量之间的趋向信息，同时考虑这两种信息，提出一种新的相似性指标来度量节点向量的相似性并进行链路预测.

3 模型与算法

本文算法的具体流程图如图1所示.首先对给定的数据集进行训练集和测试集的划分，在训练集构造的网络中分别使用DFS和BFS搜索策略获得节点序列库；将节点序列库输入CBOW模型进行训练，得到每个节点的节点向量；使用SMTV计算边的相似性分数，从而确定链路预测准确度AUC的值.

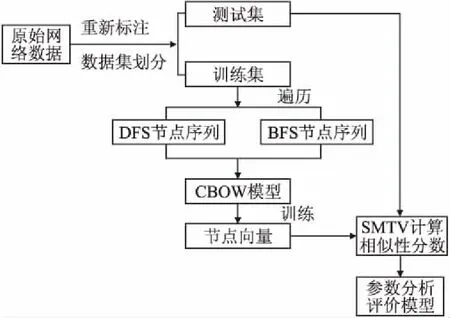
图1 CBOW-SMTV模型框架Fig.1 CBOW-SMTV model framework

3.1 CBOW模型

CBOW是一种神经概率语言模型，广泛应用于自然语言处理领域.该模型使用中心词的上下文来预测中心词概率，即在已知当前词wt的上下文：wt-n，wt-n+1，…，wt+n-1，wt+n的前提下预测当前词wt的概率，极大地考虑了周围词对于中心词的影响.模型的结构图如图2所示.

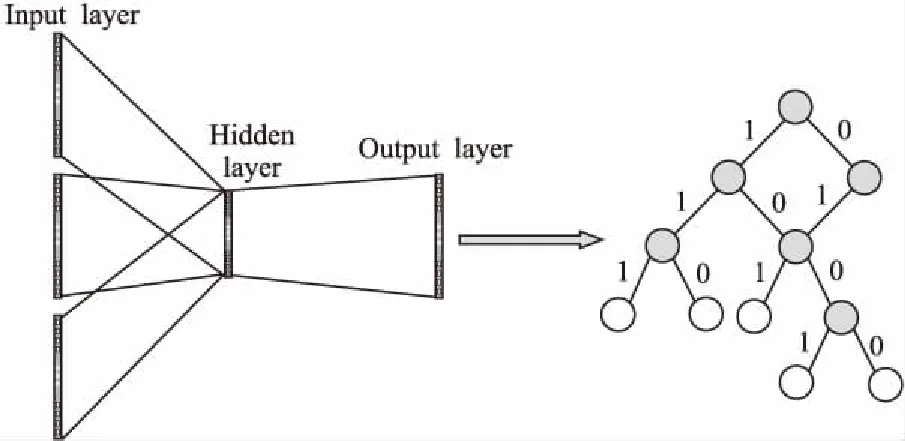
图2 CBOW模型结构图Fig.2 CBOW model structure

图2给出了的CBOW模型的网络结构，包括3层：输入层、隐藏层和输出层.输入层输入中心节点的上下文节点的初始化向量，这个向量通常是独热表示(One-hot Representation)，或者是分散表示(Distributed Representation)，这两种表示都可以对每个节点向量进行初始化表示，本文使用分散表示，克服维度灾难的困扰[18].隐藏层将输入层输入的节点向量做求和累加.输出层对应一棵哈夫曼树，这棵哈夫曼树对应一棵以节点序列库中出现过的节点为叶子节点，以各节点在节点序列库中出现的次数为权值构造出来的二叉树，采用的编码策略是将编码为1的节点定义为负类，而将编码为0的节点定义为正类.

CBOW作为基于神经网络的语言模型，对于中心词n，其优化的目标函数的形式如公式(7)所示：

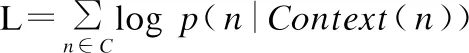
(7)

3.2 目标函数

对于节点序列库中出现每一个节点都对应输出的哈夫曼树的一个叶子节点，那么任意一个叶子节点一定存在一条从根节点到叶子节点的路径path，且这条路径唯一存在.假设这条路径中包含l个节点，则路径path上存在l-1个分支，将每个分支看作一次二分类问题，每次分类都会产生一个概率，将这些分支产生的概率相乘得到公式(7)需要的p(n|Context(n)).

(8)

公式(8)中：

(9)

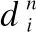
(10)

结合式(7)-式(10)，得到如公式(11)所示对数似然函数表达式，即为CBOW模型的目标函数：

(11)

简记为：

(12)

由于目标函数是对数似然函数，且表示的意义是最大化在上下文出现对应节点的情况下中心节点出现的概率，所以优化目标函数的目的就是使目标函数最大化，这里使用求最大值的随机梯度上升法.使用随机梯度上升法得到非叶子节点对应的更新函数如下：

(13)

(14)

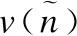
(15)

3.3 节点序列选取

使用CBOW训练模型的先导步骤就是构造节点序列库.传统构造节点序列的方法是从某一节点出发使用随机游走产生一条指定长度的节点序列，但是使用这一方法产生的序列随机性太强，即便是使用有偏向的随机游走策略[13].这种节点序列产生的是具有随机性和带有偏向随机性的节点序列.例如，从网络中的某一节点出发，为寻找下一节点而进行随机游走时，在此节点所有邻居节点中只随机选取一个，没有考虑所有邻居节点对于这个节点的影响，对于网络节点的采样具有一定局限性.本文使用从某一节点出发的深度优先搜索策略(DFS)结合广度优先搜索策略(BFS)，对网络中的节点进行采样.

DFS沿着网络中的某一节点v，尽可能深的搜索网络分支，当节点v的所在的边都被搜索过之后，搜索算法回溯到发现节点v的那一条边的起始点.这个过程一直进行到已发现从源节点可达的所有节点为止.深度优先搜索是图论中的经典算法，利用深度优先搜索可以产生目标图的相应拓扑排序表也就是本文中使用的节点序列，这个节点序列包含整个网络中每个节点的连通路径信息.BFS是从选定节点v开始，沿着节点v向周围进行搜索，如果所有节点均被访问，则算法终止.在网络中对某一节点进行广度优先搜索，如果搜索深度为1，则得到的是与这个节点直接相连的节点序列，也就是这个节点的一阶邻居信息；如果搜索深度为2，则搜索结果为直接与此节点相连的节点序列以及通过两条边间接与此节点相连的节点序列，即节点的一阶邻居信息加上二阶邻居信息.通过设定广度优先搜索策略的搜索深度2获得包含节点的共2阶邻居信息的节点序列.通过BFS和DFS策略，将得到的序列整合在一起，组成包含了网络连通性信息和节点局部信息的节点序列库，使得下一步的训练模型更具有针对性.

以图3所示为例，从节点1出发，使用深度优先搜索得到的节点序列为：{1,2,4,8,7,6,3}，包含了在此网络中从节点1出发的连通信息.使用一阶广度优先搜索得到的节点序列为：{1,2,5}，包含节点的一阶邻居信息.使用二阶广度搜索得到的节点序列为：{1,2,5,4,6}，包含了节点的二阶邻居信息.使用这些节点序列，结合CBOW模型使用中心节点的上下文节点序列信息构造节点向量的特征，能够更好的提高链路预测准确性.

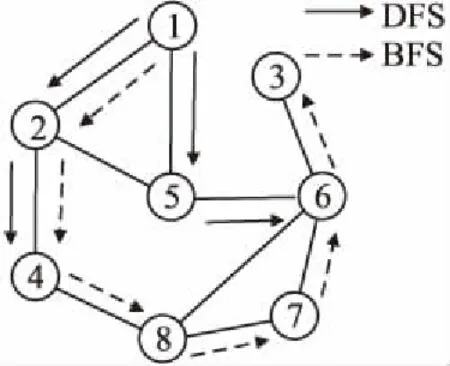
图3 BFS和DFS的序列搜索策略Fig.3 BFS and DFS sequence search strategy

3.4 SMTV指标

在得到包含网络连通性信息和节点局部信息的节点序列库之后，使用CBOW模型训练得到每个节点对应的向量表示.网络节点向量化表示之后，使得网络节点具有向量本身的特征，传统节点相似性指标在进行向量度量上不能很好表现向量的本质特性.首先，向量化的节点可以看作是在对应维度的空间中的向量，那么，两向量的延展特性可以理解为空间趋向，其相似性就可以通过两个向量的余弦相似性进行表示，余弦相似性计算如公式(16)所示：

(16)

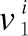
其次，向量本身的模长作为衡量向量大小的原生属性，也可以度量向量间的相似性.向量模长的计算如公式(17)所示：

(17)

结合向量原生的特征即大小和其演化表现即延展趋向，本文提出了衡量向量化节点的相似性的指标—SMTV，称为向量自量趋向性(self-measurement tendency of vector，SMTV).该指标综合考虑节点向量的原生特征及其在空间中的相互关系，通过余弦相似性度量两个节点向量在向量空间中的趋向情况，两个节点向量之间的余弦相似性越大就认为两向量的趋向性越强，两节点的相似性越高.在考虑节点趋向性的同时，将节点自身属性也加入到相似性度量中，即节点的“大小”—节点向量模长.如果两个节点向量不仅在趋向性上相似，并且向量的模长也非常接近，那么可以肯定这两个节点向量的相似性非常高.SMTV的相似性度量公式如公式(18)所示：

(18)

其中n1，n2表示节点，v1，v2表示对应的节点向量，表示可调参数，用于调节节点的趋向性和自身大小属性在相似性度量中的程度.

4 实验及结果分析

本文选取不同领域的3个真实网络数据集进行仿真实验，通过构建的CBOW模型对获取的节点序列信息进行节点向量的学习与训练，使用SMTV相似性指标完成链路预测，与一些经典链路预测方法如CN、AA、LP和使用带有回溯和偏向的随机游走方法Node2vec-Hadamard进行对比，验证本文模型的可行性和所提出相似性指标的有效性.

4.1 数据集

本文选用3个真实网络数据集进行实验：

·蛋白质互作用网络Yeast[19]：节点表示蛋白质，边表示相互作用.该网络包含2617个节点和11855条边.属于稠密网络范畴.

·社交网络数据集Facebook[20]：在Facebook数据集中，节点表示用户，边表示两个用户之间的好友关系，网络中包含4039个节点和88234条边.属于稠密网络范畴.

·电力网络Power Grid[21]：美国西部电力网络.节点表示变电站或换流站，连边表示表示它们之间的高压线.该网络包含4941个节点和6594条边.属于稀疏网络范畴.

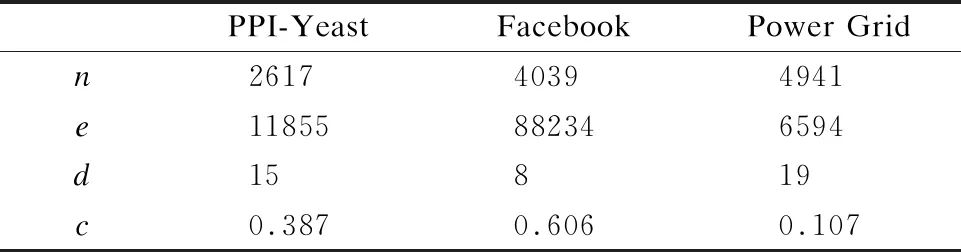
表1 仿真实验数据集的基本统计信息Table 1 Basic statistics of the simulated experimental data set

表1总结上述3个网络的基本统计特征，其中n表示网络中包含的节点数，e表示网络连边数，d表示网络直径，c表示网络的聚类系数.

4.2 评价指标

本文使用衡量链路预测算法精确度最常用的指标—AUC(Area Under the Receiver Operating Characteristic Curve)[22]从整体上衡量算法的精确度.为了对比实验的一致性，对于所有实验数据集均采用抽样比较的方法得到AUC的值.在抽样比较的前提下，AUC的含义是在测试集中随机选择一条边的分数值比随机选择一条不存在的边的分数值高的概率.也就是说，每次从测试集中随机地抽取一条边，同时从不存在的边中随机抽取一条，如果测试集随机边的分数比不存在随机边的分数大，就加1分；如果相等就加0.5分，如果小于则不加分.独立比较m次，有m′次加1分，有m″次加0.5分则AUC定义如公式(19)所示：

(19)

4.3 实验结果

本文对实验数据采用9：1的比例随机划分训练集和测试集，共进行50次独立实验，每次实验都计算相应的AUC值.将所有得到的AUC值求平均作为最终的实验结果.每次独立实验进行10000次随机抽样比较预测边与不存在的边的相似性值计算AUC.

本文使用CN、AA、LP以及Node2vec-Hadamard 4种方法设置对比实验.

通过对表2的实验数据进行分析发现，基于CBOW的SMTV指标相比其他4种方法都有提升.

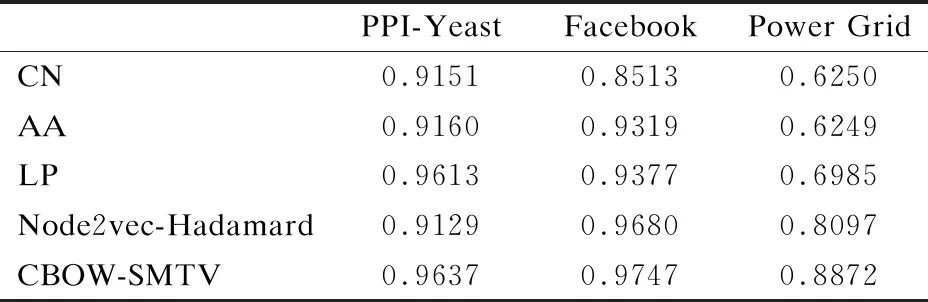
表2 各方法在不同数据集下的AUC值Table 2 AUC values for each method indifferent data sets

对于网络规模相对较小，包含较少节点但连边较多的蛋白质相互作用网PPI-Yeast来说，五种方法表现都很好，AUC值均在0.9以上，CN和AA两个基于共同邻居的方法表现相对一般，都略高于0.9，Node2vec也因为序列选择的随机性，导致AUC值较差.但是采用了二阶邻居信息的LP方法表现突出，达到了0.96以上，证明在一阶邻居的基础上考虑二阶邻居，能够得到更好的效果.因为在节点序列库中包含节点二阶邻居序列，CBOW-SMTV方法取得了和LP较为接近的结果，准确度达到了0.9637，相比效果最差的Node2vec-Hadamard方法有5.3109%的提高，比效果最好的LP方法提高了0.2497%.

在网络规模较大，节点数量和连边情况都较多的社交网络Facebook中，因为连边数量众多，每个节点都有很多的邻居的情况下，就近邻居的属性淡化了网络连通性的影响，使用CN方法直接对网络链路情况进行预测只能得到0.8513的准确度，但是在共同邻居的基础上考虑节点度的影响，AA方法的准确度就可以有较大程度提高.二阶邻居在一定程度上增加了局部的连通性，LP方法相比AA方法也有了一定的提升，Node2vec也因为采样率的提高，准确度提高更加明显.CBOW-SMTV能同时考虑网络的连通性与邻居信息使得准确度相比于Node2vec-Hadamard得到一定的提升.

在节点数量较多，网络连边较少的PowerGrid网络中，传统的CN，AA，LP方法表现欠佳，AUC都处在0.7以下.本文提出的方法取得较好的链路预测准确度，甚至相比于效果最好的Node2vec-Hadamard方法有了9.5714%的提高.对于同样使用节点向量进行链路预测的Node2vec-Hadamard方法，CBOW-SMTV因为使用同时结合网络连通信息和节点邻居信息的节点序列，在训练模型的过程中能得到更具有表现力的节点向量，利用向量的本质特征进行相似性度量，所以实验结果更好.

综上，本文提出的CBOW-SMTV方法在不同规模和类型的网络中都能表现出相对较好的预测准确性.

4.4 参数敏感性分析

本节分析CBOW-SMTV模型中的参数，包括：节点向量表示的向量维度Dimension、训练节点序列需要考虑的节点上下文序列的大小Contextsize和相似性指标中的可调参数.其中Dimension用来刻画节点向量映射空间的复杂程度，Contextsize用来衡量周围节点对中心节点的影响范围.在PPI-Yeast、Facebook、Power Grid数据集下测试各参数对于算法效果的影响，如图4所示.

在3个数据集中本文采用控制变量法分别测试了生成节点向量维度、训练CBOW模型的节点上下文节点数以及相似性指标SMTV中的参数α对于链路预测准确性AUC的影响，默认Dimension=100，Contextsize=5，α=0.4；节点向量维度的调节步长设置为20，上下文节点窗口大小步长设置为2，比例的步长设置为0.1.

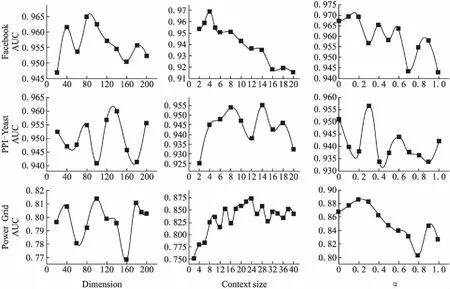
图4 CBOW-SMTV的参数敏感性分析Fig.4 Parameter sensitivity analysis of CBOW-SMTV

5 总结与展望

本文中，我们研究使用CBOW模型在网络中进行链路预测的方法，提出一种使用神经概率语言模型CBOW训练节点向量，对准确衡量节点向量的相似性，提出了SMTV相似性指标，从而进行链路预测的方法.此方法可以有效结合网络的连通信息和节点的邻居信息，更加全面地考虑节点在网络中的地位和作用，使向量表达节点的信息更加准确.实验结果表明，CBOW-SMTV方法对PPI-Yeast、Facebook和PowerGrid真实数据集均表现出良好的预测效果.

当然，本文提出的方法也存在一定的不足之处，虽然使用了多线程对于模型的训练进行了优化，但是为了使CBOW-SMTV可以适用于大部分网络和各种类型的数据集，在对数据集进行节点重新标注索引的过程中仍然耗时较大，并且在部分计算过程中出现大量占用内存的问题，一定程度上增加了程序执行时间.

后续的研究将着眼于将方法推广到包含时序的网络模型中，研究适用于时序网络的基于概率语言模型的链路预测方法.