随机障碍物下的有向传感器网络覆盖优化算法
2020-12-11关志艳黄向生
关志艳,黄向生
1(山西大学 商务学院 信息学院,太原 030001) 2(中国科学院 自动化研究所,北京 100190)
1 引 言
随着物联网时代的到来,人们对于各种监控环境信息的采集,已经不局限于温湿度、气体浓度、光感等全向传感器的采集,越来越多的情况下,像视频、超声波、红外等有向传感器对细粒度、精准信息的环境监测更为广泛[1,2].任何环境监测首先要解决的就是节点部署覆盖问题,这关乎到信息采集的全面性及准确性,对传感器网络“感知”服务质量至关重要[3,4].
有向传感器网络DSN(Directional Sensor Networks)覆盖分为区域覆盖、目标覆盖、栅栏覆盖[5].本文是在DSN区域覆盖前提下进行研究,国内外已有一些算法来提高区域覆盖质量.Sung等[6]提出将DSN划分为Voronoi单元,应用分布式贪婪算法来提高覆盖率.Kandoth等[7]提出分布式Face Away算法,以邻居节点间密度最小的方向来改善感知重叠度.大多数算法倾向于无障碍物环境下节点分布式计算,相互间交换信息再进行独立算法执行.
虚拟势场作为解决传感器网络覆盖的典型方法,自2007年陶丹等[8]第一次将虚拟势场引入有向传感器网络DSN中,近些年很多专家都对虚拟力算法VFA(Virtual Force Algorithm)应用于DSN有了各种改进.陈莹等[9]在虚拟力模型基础上建立学习自动机与环境信息的交互机制来提高覆盖质量;蒋一波等[10]对将邻居节点影响引入到质心计算中,进而调整角度机制,提高算法执行效率;肖甫等[11]将邻居节点对路径轨迹点的共同覆盖率引入虚拟斥力计算中以提高覆盖率.以上VFA均没有分析障碍物对虚拟力的影响,且对邻居节点的定义也均是以圆心间距离小于感知半径之和作为判断条件,未考虑节点方向性造成的影响,势必造成节点计算成本高等缺陷.
粒子群算法PSO(Particle Swarm Optimization)是典型的全局优化算法,张聚伟等[12]建立有向传感器模糊感知模型,将其应用于PSO中来解决路径覆盖问题;顾晓燕等[13]采用改进的多步式位置来更新粒子角度,从而减少覆盖重叠区和盲区.以上单纯粒子群算法应用于DSN,由于初始代的位置、角度及角速度都是随机分配,容易使算法陷于“早熟”,不易达到适度值最优状态.
范兴刚等[14]将VFA与PSO结合应用于有向传感器网络,对网络覆盖率有一定的改善作用,但在随机部署网络计算虚拟力后,应用粒子群算法时节点的初始角速度未考虑虚拟力影响,这就导致网络覆盖的不可控性增强,且未考虑随机障碍物的影响.
本文首次将VFA和PSO结合起来应用于随机障碍物下的有向传感器网络中,详细分析了有向概率感知模型,定义了受质心限制的邻居节点,分析了VFA应用于障碍物DSN的虚拟力计算,虚拟合力与旋转角度之间的关系,用PSO来弱化VFA的局部极值效应,仿真实验表明受障碍物影响的VFA融合PSO的DSN覆盖算法能有效改善随机障碍物下DSN的覆盖盲区和重叠区.
2 DSN分析
2.1 有向感知能力衰减概率模型

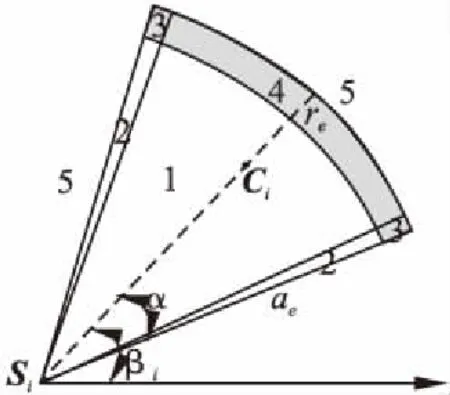
图1 有向感知能力衰减概率模型Fig.1 Directed sensor reduction probability model
凡是在扇形感知区域内的目标均被感知,但有的有向传感器节点的感知能力会随感知方向向两侧衰减和由内向外衰减,目标监测点会因为在扇形区不同区域,呈现不同的感知概率[15].如图1所示,将扇形划分为5个区域,1区域完全在扇形感知区,2区域接近扇形两侧,4区域接近扇形外侧,3区域则是扇形两侧与外侧交织处,2、3、4区域感知概率会有不同程度衰减.
如图1所示αe为衰减偏移角度,re为衰减感知长度,目标点Mj在扇形区域5个分区的感知概率见式(1):
(1)
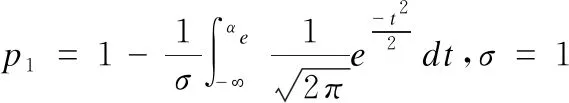
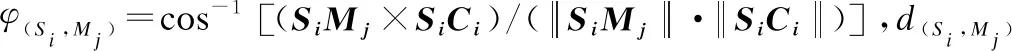

表1 有向扇形5分区关系表Table 1 Directed sector 5 partition relation table
不同的有向传感器有不同的衰减方式,有的传感器并不会两侧或外侧衰减,如视频节点、超声波节点,因此在细粒度目标感知时,需要参照有向感知能力衰减模型具体情况具体分析.
2.2 障碍物下的有效覆盖率
针对障碍物下的有向传感器网络区域覆盖,用尽量少的节点达到避障下最大的覆盖面积是区域覆盖的优化方向.有向传感器节点部署在监测区域后位置不变,感知视角可调,因此最优有效覆盖率则是求取一组<β1,β2,…,βn>的有向节点使除去与障碍物重叠的覆盖总面积(重叠面积不重复算)与监测面积之比达到最大.
(2)
其中A为监测区域面积,B为障碍物面积,A=l·k,l、k为监测区域长与宽,Ai为有向节点覆盖面积,Bi为节点i与障碍物的重叠面积.当满足初始有效覆盖率CE0时需要的传感器节点规模为[9]:
(3)
3 障碍物虚拟力分析
3.1 问题描述
本文主要研究区域覆盖,旨在经过算法求得一组<β1,β2,…,βn>,以使有效覆盖率最大化.所有有向传感器节点同构,采用五元组扇形模型.真实环境下必然遇到节点能量供给不均衡、感知不灵敏及监测环境的不可控性等情况.本文在matlab下进行仿真,有些条件是理想化的,因此有必要做以下假设:
1)有向传感器节点为计算能力较强的智能传感器,采用分布式节点计算,每个节点兼顾网络终端和路由双重功能.每个节点收集到其他节点位置信息后,会在自身执行算法[16];
2)初始随机部署后,位置将不再移动,只调整角度,节点可通过自身GPS获得圆心坐标Si,感知视域夹角2α;
3)整个监测环境为矩形平面区,通信半径大于2Rs,监测区域完全连通,不考虑信道对称性、多径和衰减等问题[17].
3.2 邻居节点虚拟力分析

(4)
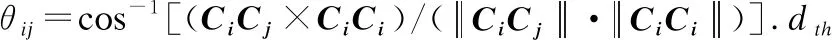
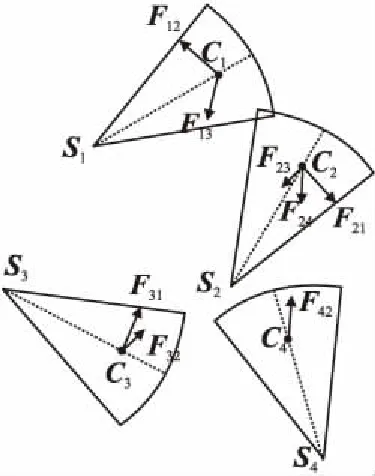
图2 邻居节点间受力模型Fig.2 Virtual force model between neighbor nodes
如图2所示,分析有向节点S1、S2、S3、S4间的作用力,以S1为分析点,d12<1.5dth,S2对S1为斥力F12;d13≥1.5dth,S3对S1为引力F13;S4与S1非邻居节点,它们之间没有作用力.将Fij分解成垂直于感知方向的分量Fij′和指向节点圆心方向的分量Fij″,Fij′=Fij·sinθij,Fij″=Fij·cosθij.
3.3 障碍物与节点间斥力分析
在监测环境下,难免会有障碍物,有向传感器节点尽量避开与障碍物的大面积重叠,如图3所示,Oj为障碍物,本文假设障碍物为类似于此的矩形区.
FiOj=(ρb/diOj,θiOj+π)
(5)
其中ρb为障碍物斥力参数,ρb与障碍物面积SOj成正比,ρb=SOj/(α·Rs2),diOj为Ci到Oj的距离,θiOj为FiOj的方向角度,其计算与θij类似,对于FiOj′、FiOj″的分量拆解与Fij类似.
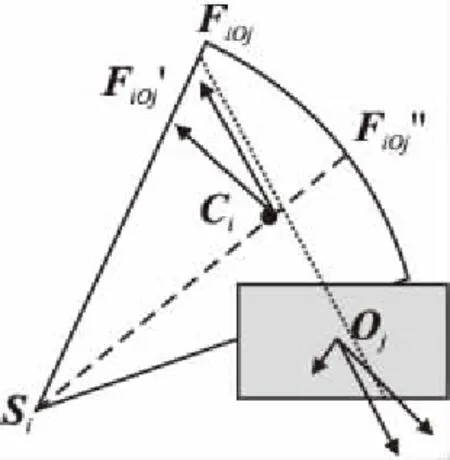
图3 障碍物斥力模型Fig.3 Barrier repulsion model
3.4 虚拟合力分析
每个节点都有可能受多个邻居节点、多个障碍物的影响,节点所受虚拟力均可拆分成垂直感知方向的分量(即切线分量)和指向节点圆心的分量(即向心分量),k1、k2为节点i的邻居节点个数和邻居障碍物个数,两分量之和分别为:
(6)
3.5 转动角度计算
从动力学角度分析,可知节点转动角度由向心分量Fi′和切线分量Fi″共同决定,假设在Δt时间内Fi′、Fi″不变.
3.5.1 切线方向
(7)
3.5.2 向心方向
本文分析的节点所受虚拟力由物理学圆周运动可知‖Fi″‖=γ·vt2·Rs,vt为向心力提供的角速度.
(8)
结合式(7)、式(8),节点i所受虚拟斥力的转动角度Δθi:
Δθi=kθ·(Δθi′+Δθi″)
(9)
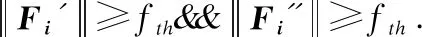
3.6 障碍物影响下虚拟力算法流程
1)初始化网络节点规模n,邻居节点引力系数ρg,斥力参数ρr,障碍物斥力系数ρb,视域范围2α,感知半径Rs,随机部署n个有向传感器节点,自动获取圆心坐标,感知方向夹角,经过计算可获得质心坐标,节点生成五元组感知模型.
2)设置最大循环次数Hmax
for loop=1:Hmax
{fori=1:n%建立n×n矩阵,存放节点间距离
{forj=1:n
{计算节点i,j的圆心距离Dij和质心距离dij;
if(dij<2Rs&&Dij<2Rs) %判断是否邻居节点
{建立节点的邻居节点质心距离dij矩阵;
式(4)计算邻居节点间引力斥力Fij及Fij′、Fij″;}
}
}
forj=1:k2%计算节点与障碍物间斥力
{计算diOj;
if(diOj<2RS)
式(5)计算FiOj及FiOj′、FiOj″;
式(6)计算节点i在切线方向和向心方向的分量合力;
式(7)-式(9)计算节点i旋转角度Δθi,对节点进行二维灰度变化求得有效覆盖率;}
}
依据障碍物影响下虚拟算法流程,假设在100m×100m监测区域内,分布一个矩形障碍物,假设初始覆盖率至少达到50%,由式(3)计算需要50个90°视域Rs=12m的有向传感器节点,经过10次随机分布节点障碍物,每次迭代30次,观察网络有效覆盖率情况,图4可以看出,经过虚拟力算法节点分布均匀化,但由于避障手法单一而使障碍物附近出现覆盖空洞效应.
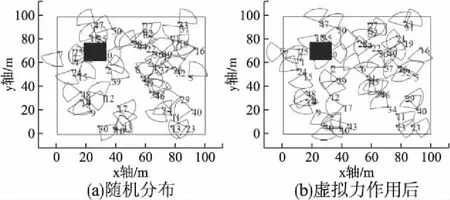
图4 虚拟力作用节点分布对比图Fig.4 Contrast figure after virtual force
4 障碍物下的虚拟力融合粒子群的DSN覆盖分析
4.1 粒子群模型
本文将DSN中的大量有向传感器节点简化为平面内没有质量且允许旋转的粒子,粒子据适度值函数来衡量粒子位置优劣,粒子旋转角速度和角度受自身旋转经验和邻居粒子的旋转经验来进行综合调整[19,20],每次迭代中,粒子据式(10)更新角速度和感知方向水平夹角.
(10)
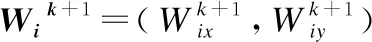
(11)
4.2 虚拟力融合粒子群覆盖算法
本文在传统粒子更新速度公式中加入虚拟力作用下的旋转角度的影响,并且将随机分布下受障碍物虚拟力作用的角速度,作为粒子群第0代的初始角速度,粒子据式(12)更新角速度和感知方向水平夹角.
(12)
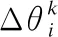
(13)
4.3 障碍物下的虚拟力融合粒子群DSN覆盖算法流程
基本思想:首先随机分布节点,分布式计算每个节点所受虚拟合力,在合力作用下的旋转角度及角速度;然后节点粒子化,将随机分布下的角速度及旋转角度,作为粒子群第0代的初始角速度,据更新公式进行粒子进化;最后以网络有效覆盖率为适度值函数来得到节点迭代最优解.
1)初始化网络粒子规模n,学习因子a1、a2、b1、b2,虚拟力影响加速因子av、bv,最大迭代次数tmax;
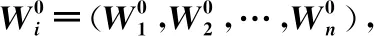
3)fork=1:tmax
{fori=1:n
matlab下对节点进行二维灰度变化求得有效覆CEK+1;
if(CEK+1>CEK)
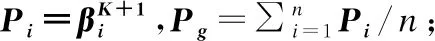
}
4)CEmax=max(CE0,CE1,…,CEtmax)
5 算法仿真与性能分析
5.1 实验参数设定
本文利用matlab在随机部署矩形障碍物的监测环境下,利用虚拟力融合粒子群覆盖算法仿真,主要进行三方面观察:
1)通过实例展示算法适度值优化效果;
2)对虚拟力算法(VFA)和虚拟力融合粒子群算法(VFA-PSO)进行收敛效果验证;
3)不同网络参数对虚拟力融合粒子群算法(VFA-PSO)性能的影响.
实验涉及到的参数如表2所示.

表2 参数列表Table 2 List of parameters
5.2 实例效果
5.2.1 算法适度值优化效果比较
首先在表2所示的监测环境下,初始预估覆盖率至少达到60%,随机部署Rs=12m,2α=π/2的有向传感器节点需100个(据式(3)计算可得n=90,但考虑到监测环境覆盖稍微冗余,故n=100),随机部署3个矩形障碍物于监测环境下,观察实例效果,由于随机部署的随意性较大,算法优化后的效果也有质量差异,因此某次的实验效果不具有代表性,本文对20次随机部署进行统计观察,有效覆盖率则取50次迭代对应算法作用后CE的平均值,来提高实验普适性,减少误差.图5是实验的一次采样,图5(a)是随机部署3个障碍物于监测环境下,图5(b)是VFA算法迭代过程的一次,并不能确保迭代到最后的优化效果一定是最好的,单可以看出节点分布比随机分布更均匀些,图5(c)经过VFA-PSO算法迭代过程的一次,节点覆盖更均匀,且障碍物的覆盖空洞效应也有所改善.在这20次随机部署中,并不是每一次算法后效果都如图5(c)所示,如何能够更加稳定地发挥VFA-PSO算法优化效果将是下一步工作的重点,这可能与VFA、PSO参数有关,只有经过大量的实验总结才能找到最佳网络参数.
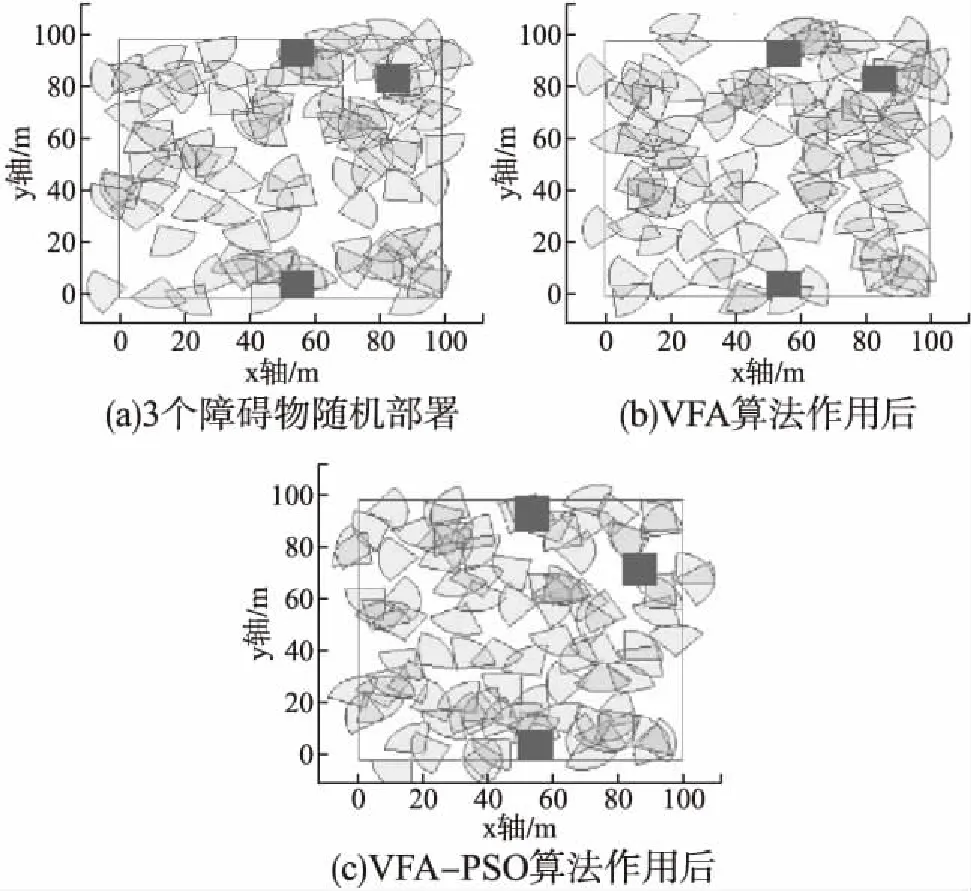
图5 3个随机障碍物下算法节点分布对比图Fig.5 Contrast deployment after algorithm by three obstacles
5.2.2 算法收敛效果分析
本文以3个障碍物环境下的20次初始预估覆盖率60%的随机分布的网络有效覆盖率CE优化为分析蓝本,VFA、VFA-PSO以50次循环迭代为一次算法周期,并将20次随机分布下算法相同迭代次数下的CE平均值作为观察对象,这样可以相对减少算法发挥的不稳定性,图6可以看出,VFA-PSO算法迭代到30次附近,CE没有明显变化趋于稳定,VFA迭代到50次,CE趋于稳定,整体来看,VFA-PSO的收敛速度更快,迭代几乎是VFA算法的一半.
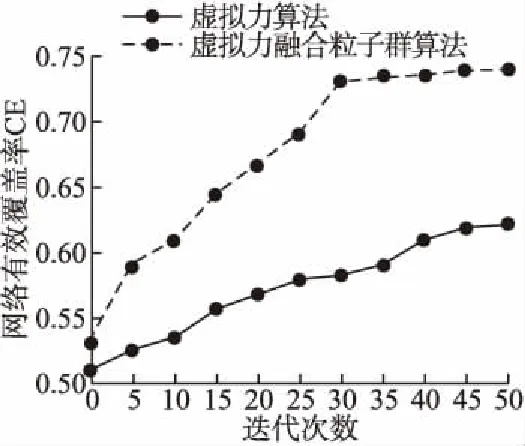
图6 算法收敛对比图Fig.6 Convergence contrast diagram of algorithm
5.2.3 不同网络参数对算法性能的影响
本文主要讨论节点数量n和感知半径Rs对网络优化的影响.增加一定数量的节点,某种程度上可以提高网络有效覆盖率CE,但同时增加开销,用最少的节点达到最大的CE是算法优化的方向之一.
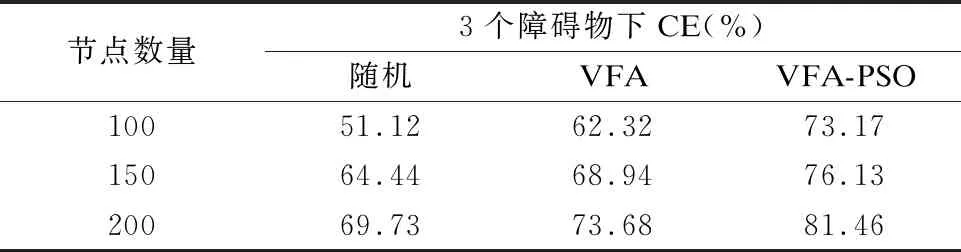
表3 两种算法随节点数量变化CE(%)比较表Table 3 Comparisons of CE(%)with the number of nodes
表3 是以3个随机障碍物下的节点数量对CE的影响,结合图6观察可以看出,初始预估覆盖率设定为60%,但实际做实验仿真下3个障碍物下20次随机部署下的初始覆盖率是51.12%,节点数量为100个时,经过两种算法覆盖率分别比初始随机部署下提升11.2%和22.05%,同样情况150个节点的初始随机覆盖率是64.44%,经过两种算法覆盖率分别提升4.5%和11.69%,可见随着节点数量的增加,并不能使CE有明显提高,而且增加网络开销,因此节点数量的确定还要综合项目成本,达到均衡.
图7为感知半径对算法的影响,Rs太小或太大对CE的提高改善都不明显,太小容易产生覆盖盲区,太大又容易产生覆盖重叠,图7可以观察在监测范围内,当节点半径为10m和12m时,对网络有效覆盖率的提升最高,这是图5-图7及表3的数据都是在Rs=12m的基础上进行的原因.
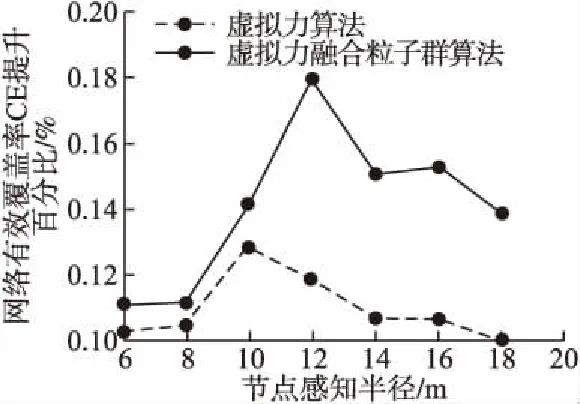
图7 感知半径影响Fig.7 Perception radius effect
6 结束语
本文研究了在随机障碍物下的有向传感器网络中,如何应用虚拟力算法和粒子群算法来有效改善网络避障效果差及覆盖重叠区空洞区等问题.单独的虚拟力算法对网络有一定的改善作用,但易出现障碍物附近覆盖空洞效应.将节点抽象成粒子模型来弱化虚拟力算法的局部极值效应,从仿真实验可以看出将虚拟力算法和粒子群算法融合后的算法对覆盖率效果明显,提高将近20%,收敛速度也更快.后续将从以下两方面继续深入研究:
1)涉及到虚拟斥力、引力参数、运动比例参数、学习因子等很多参数选定对算法至关重要,本论文中的参数是在参考了大量文献的基础上,在实验中不断测试取效果最佳情况下的值,后续将深入对算法参数等方面的研究;
2)本文算法并未分析算法能耗,而这对于能量受限的传感网络非常重要,后续将结合真实节点实验完善能耗研究.
